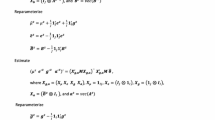Abstract
The normal way of fitting a bilinear model to values of a quantitative variable classified by rows and columns is first to fit the main effects of rows and columns and then fit a biadditive model to the residual table. This gives the ordinary least squares optimal fit, usually visualised by biplots and, among other applications areas, is routinely used in genotype \(\times \) environment trials. When the dependent variable is categorical, Fisher (1938) proposed scoring the categories by maximising the sum-of-squares of the row and column main effects relative to the residual sum-of-squares; then, the usual biadditive analysis again becomes available, although not used by Fisher. In this paper, it is shown that with categorical variables Fisher could have derived scores by maximising the sum-of-squares of the biadditive part of the model relative to the residual sum-of-squares. With Fisher’s data, this would have three advantages: (i) a better fitting model, (ii) a more parsimonious model and (iii) novel and more powerful visualisation techniques for expressing interactions. Other ways of partitioning the contributions from main effects and biadditivity are also discussed. The results show how small changes in model construction can have profound effects on interpretation. Potential applications extend far beyond the data used by Fisher to whenever the categorical nature of the dependent variable offers the freedom to generate quantifications with generalised interaction parameterisations. Supplementary materials accompanying this paper appear on-line.





Similar content being viewed by others
References
Choulakian, V. (1996). Generalized bilinear models. Psychometrika 61, 271–283.
Cox, D. R. (2016). Some pioneers of modern statistical theory: A personal reflection. Biometrika 103, 747–759.
Denis, J-B. and Gower, J. C. (1994). Biadditive models. Biometrics 50, 310–311.
Denis, J-B., and Gower, J. C. (1996). Asymptotic confidence regions for biadditive models: Interpreting genotype-environment interactions. Applied Statistics 45, 479–493.
De Falguerolles, A. and Francis, B. (1992). Algorithmic approaches for fitting bilinear models, in Y. Dodge and J. Whittaker (Eds), COMPSTAT 1992, Physica-Verlag, Heidelberg, 77–82.
De Leeuw, J., Young, F. W., and Takane, Y. (1976). Additive structure in qualitative data: An alternating least squares method with optimal scaling features. Psychometrika 41, 471–503.
Fisher, R. A. (1938). Statistical Methods for Research Workers (7\({\rm th}\) edition). Oliver and Boyd, London.
Fisher, R. A. and Mackenzie, W. A. (1923). Studies in crop variation. II, The manurial response of different potato varieties. Journal of Agricultural Science 13, 311–320.
Gauch, H. G. (1992). Statistical analysis of regional yield trials: AMMI analysis of factorial designs. Elsevier Science Publishers, Amsterdam.
Gifi, A. (1990). Nonlinear multivariate analysis. John Wiley & Sons Ltd., Chichester.
Gilbert, N. (1963). Non-additive combining abilities. Genetics Research 4, 65–73.
Gollob, H. F. (1968). A statistical model which combines features of factor analytic and analysis of variance techniques, Psychometrika 33, 73–115.
Gower, J. C. (1990). Fisher’s optimal scores and multiple correspondence analysis. Biometrics 46, 947–961.
Gower, J. C., Le Roux, N. J. and Gardner-Lubbe, S. (2015). Biplots: Quantitative data, WIREs, Computational Statistics 7, 42–62.
Gower, J. C., Le Roux, N. J. and Gardner-Lubbe, S. (2016). Biplots: Qualitative data, WIREs, Computational Statistics 8, 82–111.
Gower, J. C., Lubbe, S. and Le Roux, N. J. (2011). Understanding biplots. John Wiley and Sons Ltd., Chichester.
Guttman, L. (1941). The quantification of a class of attributes: a theory and method of scale construction. In P. Horst (Ed.), The prediction of personal adjustment. New York: SSRC.
Kruskal, J. B. (1965). Analysis of factorial experiments by estimating monotonic transformations of the data. Journal of the Royal Statistical Society, B 27, 251–263.
Martens, H. and Martens, M. (2000). Multivariate analysis of quality: An introduction. John Wiley and Sons Ltd., Chichester.
McCullagh, P. and Nelder, J. A. (1989), Generalized linear models. Chapman & Hall/CRC, Boca Raton, Florida.
Naes, T., Brockhoff, P.B. and Tomic, O. (2010). Statistics for sensory and consumer science. John Wiley and Sons Ltd., Chichester.
Van Eeuwijk, F. A. (1993). Practicalities of the use of diagnostic biplots in model choice for two-way tables. In: Proceedings of the 4 \(^{th}\) Conference of the International Federation of Classification Societies, 85–86. Paris: E.N.S.T.
Van Eeuwijk, F. A. (1995). Multiplicative interaction in generalized linear models. Biometrics 51, 1017–1032.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Gower, J.C., Gardner-Lubbe, S. & Le Roux, N.J. Interaction: Fisher’s Optimal Scores Revisited. JABES 23, 92–112 (2018). https://doi.org/10.1007/s13253-017-0311-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13253-017-0311-8