Modeling and simulation of transition zones in tight carbonate reservoirs by incorporation of improved rock typing and hysteresis models

Abstract

Transition zones in tight heterogeneous carbonate reservoirs contain a considerable amount of original oil in place. Identifying and characterizing the petrophysical flow units of the transition zone is crucial for reserve estimation and performance prediction. This paper presents a petrophysical rock typing method based on decoding pore-size distributions from mercury injection capillary pressure (MICP) data by using Thomeer hyperboles, with proven application in a tight carbonate reservoir in the Middle East region. In this study, 150 MICP data sets were used which were type curve matched using Thomeer Hyperbolas with closure correction. Multivariate clustering method has been employed to divide the samples into a number of groups for the purpose of both representing the reservoir heterogeneity and simplifying rock typing for dynamic modeling. From the MICP curves, it has been found that mainly monomodal pore systems prevail in the targeted transition zone and five different rock types are identified. It has been observed that most of the pore throat types are meso and micro types with the negligible existence of nano-pore type. The intrinsic advantage of this rock typing method is to describe the pore system quantitatively, which is different from other rock typing methods based on the apparent poro-perm relationship. The comparison of the grouped data with the petrophysical properties showed that different pore-size distributions yield similar porosity and permeability values, reinforcing the importance of grouping rocks based on pore systems instead of their resulting properties. Additionally, a study has also been conducted to improve understanding on the relative permeability in transition zone by implementing an up-to-date model for the mix-wet condition. The work in this paper provides a guide for the further understanding of rock typing and modeling of transition zones in carbonate reservoirs.

Introduction

The interval from the water–oil contact (OWC) to the height where water saturation attains its irreducible level is called transition zone of a reservoir (Bera and Belhaj 2016; Masalmeh et al. 2007; Spearing et al. 2014). In tight carbonate reservoirs, the transition zone contains a considerable amount of original oil in place due to high capillary pressure phenomena. The flow units are mainly characterized by different size and geometry of pore systems. Pore systems provide primary control on hydrocarbon distribution in the reservoir. They also control the interaction between rock and fluid in terms of capillary pressure, relative permeability, and microscopic displacement efficiency (Clerke 2007; Clerke et al. 2008). Therefore, understanding the petrophysical flow units within the transition zone and correlations of capillary pressure and relative permeability study is important for performance prediction, transition zone reservoir modeling and simulation (Shi et al. 2017). Selection of a suitable mathematical model for the correlation study also signifies the importance of capillary pressure and relative permeability hysteresis incorporation in the reservoir model for transition zone behavior prediction. Precise rock typing is another important issue in transition zone reservoir modeling and simulation. The purpose of rock typing is to classify the reservoir rocks into different units with respect to pore system, texture, and lithotypes.

It is also important to mention that in some cases, the amount of oil contained in transition zones of the reservoirs is relatively low compared to the total oil in place. Therefore, development of such reservoirs is not beneficial for economic purpose. But if a reservoir with transition zone contains a significant amount of oil then it is very important to develop such reservoirs for oil production to perforate the transition zones. For this purpose, it is necessary to understand the reservoir fluid flow behavior in transition zones. As it is well known that both oil and water are movable in the transition zone, it is essential to understand the complexity of the transition zone before modeling and simulation to predict the production performance. However, if the transition zone in the reservoir is large enough, then the uncertainty exists in the variation of relative permeability, capillary pressure, and residual oil saturation with the initial water saturation (Spearing et al. 2014).

Traditional rock typing methodologies for carbonate reservoirs typically are based on the routine core analysis (RCA) data with well logs and a small subset of MICP tests. These methods include cutoff-based clustering method, Flow Zone Indicator (FZI)/Reservoir Quality Index (RQI) method, Winland/Pittman R₃₅ method, and Leverett J-function method. These methods have been extensively used in the literature before (Amaefule et al. 1993; Francesconi et al. 2009; Rincones et al. 2000; Skalinski et al. 2005; Venkitadri et al. 2005). The cutoff-based clustering method is based on porosity or permeability ranges or even a combination of both terms. Amaefule et al. (1993) introduced FZI and RQI methods for rock typing and thereafter these methods have been used widely in the literature (Gunter et al. 1997; Porras and Campos 2001; Jennings Jr and Lucia 2003; Rincones et al. 2000; Soto et al. 2001). The following equations are used to calculate the FZI and RQI methods:

$$ {\text{FZI}} = \left( {0.314\sqrt {k/\phi_{\text{e}} } } \right)\left[ {\left( {1 - \phi_{\text{e}} } \right)/\phi_{\text{e}} } \right] $$

(1)

$$ {\text{RQI}} = {\text{FZI}} \times \frac{{\phi_{\text{e}} }}{{1 - \phi_{\text{e}} }} $$

(2)

where Φ_e is the effective porosity and k is permeability.

The Winland/Pittman R₃₅ method was developed by Winland and latterly improved by Pittman (1992) based on sandstone field study. It is an empirical law equation, defining R₃₅, the pore throat radius at S_Hg = 35% from MICP data, as the largest connected pore throat in a rock with intergranular porosity. The rock types are then generated by R₃₅ values.

$$ \log R_{35} = 0.732 + 0.588\,\log k - 0.8641\,\log \phi $$

(3)

The Leverett J-function approach is based on permeability, porosity and MICP data, widely used for different types of fields. It is expressed as follows although Leverett J-function approach is not recommended for carbonate reservoirs characterization (Leverett 1941):

$$ J_{\text{SW}} = 3.162\sqrt {\frac{k}{\phi }} \frac{{P_{\text{c}} }}{{\sigma \text{Cos} \theta }} $$

(4)

where P_c is the capillary pressure, σ is the interfacial tension and θ represents the contact angle.

The above-mentioned rock typing methods, however, are based on petrophysical properties or empirical knowledge. To overcome these limitations, rock typing based on Thomeer hyperboles has been implemented to capture the geometry of different pore systems and can be tied with different geological information of the reservoir.

In the present work, rock typing was done by Thomeer hyperbole method with decoding pore system for 150 MICP curves of a Middle East carbonate reservoir. Previously this method has been used in our work for 64 MICP curves (Pinto et al. 2016). In addition, MICP data clustering was also conducted to distinguish different rock types. Different hysteresis models were tested to find out the best-fitted one for dynamic modeling purpose. Incorporation of hysteresis in the dynamic model showed different results when compared to the model built without hysteresis.

Methodology

Theoretical background of Thomeer hyperbola rock typing

Thomeer (1960) observed that the capillary pressure data from MICP experiments can be fitted with a hyperbola by using three fitting parameters like G, P_d, and $\left( {V_{\text{b}} } \right)_{{P_{\infty } }}$ as shown in Eq. (5):

$$ \frac{{\left( {V_{\text{b}} } \right)_{{P_{\text{c}} }} }}{{\left( {V_{\text{b}} } \right)_{{P_{\infty } }} }} = \exp^{{ - G/\left( {\log {\raise0.7ex\hbox{${P_{\text{c}} }$} \!\mathord{\left/ {\vphantom {{P_{\text{c}} } {P_{\text{d}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${P_{\text{d}} }$}}} \right)}} $$

(5)

where G is the shape factor of the hyperbola curve, determined by the pore geometry and related to the range of pore throats (typically 0.1 < G < 2). P_d is the displacement pressure required for mercury to intrude the largest pore-throat in the rock (in psi) and P_c is the capillary pressure. $\left( {V_{\text{b}} } \right)_{{P_{\text{c}} }}$ is the bulk volume occupied at capillary pressure and $\left( {V_{\text{b}} } \right)_{{P_{\infty } }}$ represents the percentage of bulk volume invaded by mercury at infinite pressure ($P_{\infty } )$ (Fig. 1). For a rock with unimodal pore system, one hyperbola is used to fit with the experimental data while for a rock with bimodal or trimodal pore system, two or three hyperbolas can be combined together to match the data, with each pore system’s geometry (G factor) and volume ($\left( {V_{\text{b}} } \right)_{{P_{\infty } }}$) represented.

Fig. 1

Thomeer hyperbola with three fitting parameters illustrating the pore system geometry

MICP data clustering

By clustering the Thomeer parameters of each MICP data, different rock types can be distinguished. The clustering method used here is the K-means clustering technique. K-means clustering aims to partition the input observations into different clusters in which each observation belongs to the cluster with the nearest mean, and the center of each cluster is taken as the average capillary pressure curve. Their error bounds can be obtained as follows (Buiting and Clerke 2013; Buiting 2011):

$$ J = \sum\limits_{j = 1}^{k} {\sum\limits_{i = 1}^{n} {\left\| {\overrightarrow {{x_{i}^{(j)} }} - \overrightarrow {{c_{j} }} } \right\|} }^{2} $$

(6)

where $\left\| {\overrightarrow {{x_{i}^{(j)} }} - \overrightarrow {{c_{j} }} } \right\|^{2}$ is the distance between the Thomeer parameter vector $\overrightarrow {{x_{i}^{(j)} }}$ and cluster center $\overrightarrow {{c_{j} }}$, J is the objective function which needs to be minimized by tuning the cluster center.

Rock typing and decoding pore system

This study uses a set of 150 MICP curves from a well in the transition zone of a carbonate reservoir in the Middle East region as shown in Fig. 2. The MICP data come along with conventional core analysis data from the laboratory experiment with some cores further experimented on for the drainage and imbibition curves. Due to Mercury not completely filling the empty volume of core container and the cutting problems in core preparation(such as rough surface), conformance correction is carried out using the inflection point analysis before the raw MICP curves are processed for Thomeer hyperbola matching. Pore throat distribution can then be calculated based on the MICP data and the modality of pore systems of each core plug can be detected from the distribution curve. Finally, the MICP curves are matched by the Thomeer hyperbola parameters using the Clerke and Martin Thomeer spreadsheet as shown in Fig. 3 (Clerke and Martin 2004).

Fig. 2

MICP dataset from core plugs in transition zone from a tight carbonate reservoir

Fig. 3

Thomeer hyperbola matching using Clerke spreadsheet where two hyperbolas (blue and yellow) represent different pore system to match the MICP curves

Modeling and simulation

Numerical modeling of mixed-wet systems with a thick transition zone typically requires the full hysteresis option to be invoked in the reservoir simulator, and this requires preparing all the bounding curves for each rock type. It is crucial to express the relationship between capillary pressure, relative permeability, and saturation to facilitate generating scanning curves for dynamic modeling.

Previously, a number of models have been proposed to correlate capillary pressure and relative permeability with water saturation (Killough 1976; Carlson 1981; Skjaeveland et al. 2000; Masalmeh et al. 2007; Nono et al. 2014). However, Killough and Carlson models are developed for a water-wet condition which does not represent the real situation in the transition zone. The models also make use of Land’s type S_oi and S_or relationship (Land 1968), which is not fit for our mixed-wet transition zone case. Skjaeveland et al. (2000) introduced the oil-wet branch referring from the Brooks and Corey method of water-wet branch equation and extended it to the mixed-wet reservoir for capillary pressure correlation, Skjaeveland’s relative permeability hysteresis model shows better predictions but requires a lot of inputs that are not always available at laboratory scale. Masalmeh et al. (2007) introduced a modified Darcy method which is fit for the intermediate-wet system. Nono et al. (2014) presented their hysteresis experiment on two unimodal and bimodal pore system of carbonate rocks and present a new k_r hysteresis model, using the bounding k_r (relative permeability) curves and incorporating wettability change, which is quite promising for dynamic modeling of the transition zone. Hysteresis models for different wetting conditions are discussed in the following sections.

The Killough (1976) hysteresis model

The Killough model for relative permeability was developed based on the Land’s correlation of relative permeability hysteresis. Land’s method was generally considered for determination of imbibition relative permeabilities. Killough used a parametric interpolation method using the following equation:

$$ k_{\text{rN}}^{\text{Im}} \left( {S_{\text{N}} } \right) = k_{\text{rN}}^{\text{Dr}} \left( {S_{\text{N}}^{\text{Hyst}} } \right).\left( {\frac{{S_{\text{N}} - S_{\text{Nr}} }}{{S_{\text{N}}^{\text{Hyst}} - S_{\text{Nr}} }}} \right)^{\lambda } $$

(7)

where $\lambda$ is a given parameter.

When normalized experimental results are available, then the above equation can be modified as follows:

$$ k_{\text{rN}}^{\text{Im}} (S_{\text{N}} ) = k_{\text{rN}}^{\text{Dr,Exp}} (S_{{{\text{N}} }}^{\text{Hyst}} ) \times \left[ {\frac{{k_{\text{rN}}^{{\text{Im} b , {\text{Exp}}}} (S_{{{\text{N}} }}^{\text{Norm}} ) - k_{\text{rN}}^{{\text{Im} b , {\text{Exp}}}} (S_{\text{Nr}}^{\text{Max}} )}}{{k_{\text{rN}}^{{\text{Im} b , {\text{Exp}}}} (S_{{{\text{N}} }}^{\text{Max}} ) - k_{\text{rN}}^{{{\text{Im}}b , {\text{Exp}}}} (S_{\text{Nr}}^{\text{Max}} )}}} \right] $$

(8)

where $S_{\text{N}}^{\text{Norm}} = \left[ {\frac{{(S_{\text{N}} - S_{\text{Nr}} ) \times (S_{\text{N}}^{\text{Max}} - S_{\text{Nr}}^{\text{Max}} )}}{{S_{\text{N}}^{\text{Hyst}} - S_{\text{Nr}} }}} \right] + S_{\text{Nr}}^{\text{Max}}$

On the other hand, imbibition (k_rw) for a given trapped nonwetting-phase saturation (S_N) can be calculated by using the following equation:

$$ k_{\text{rw}}^{\text{Im}} (S_{\text{N}} ) = k_{\text{rw}}^{\text{Dr,Exp}} (S_{\text{N}}^{\text{Hyst}} ) + \left[ {\frac{{k_{\text{rw}}^{\text{Im,Exp}} (S_{\text{N}}^{\text{Norm}} ) - k_{\text{rw}}^{\text{Im,Exp}} (S_{\text{N}}^{\text{Max}} )}}{{k_{\text{rw}}^{\text{Im,Exp}} (S_{\text{Nr}}^{\text{Max}} ) - k_{\text{rw}}^{\text{Im,Exp}} (S_{\text{N}}^{\text{Max}} )}}} \right] \times \left[ {k_{\text{rw}}^{\text{Im,Exp}} (S_{\text{Nr}} ) - k_{\text{rw}}^{\text{Dr,Exp}} (S_{\text{N}}^{\text{Hyst}} )} \right] $$

(9)

The Masalmeh et al. (2007) model (modified Corey model)

The oil relative permeability is expressed as:

$$ k_{\text{ro}} = k_{\text{ro}}^{\text{Dr}} \left( {S_{\text{oi}} } \right) \times \left[ {\frac{{S_{\text{o}} - S_{\text{or}} \left( {S_{\text{oi}} } \right)}}{{S_{\text{oi}} - S_{\text{or}} \left( {S_{\text{oi}} } \right)}}} \right]^{{n_{\text{o,Im}} \left( {S_{\text{oi}} } \right)}} + \frac{{c\left( {S_{\text{oi}} } \right)}}{{1 + c\left( {S_{\text{oi}} } \right)}}\left[ {\frac{{S_{\text{o}} - S_{\text{or}} \left( {S_{\text{oi}} } \right)}}{{S_{\text{oi}} - S_{\text{or}} \left( {S_{\text{oi}} } \right)}}} \right] $$

(10)

where S_or(S_oi), $k_{\text{ro}}^{\text{Dr}} \left( {S_{\text{oi}} } \right)$, and $n_{\text{o,Im}} \left( {S_{\text{oi}} } \right)$ are the residual oil saturation, the endpoint oil relative permeability in drainage, and the Corey exponent, respectively, and c(S_oi) is a fitting parameter to adjust the oil relative permeability to match the experimental values. The constraint for c(S_oi) is that its maximum value is 0.005. S_or(S_oi) which is determined by a linear correlation, shown as the following equation:

$$ S_{\text{or}} \left( {S_{\text{oi}} } \right) = \frac{{S_{\text{oi}} \times S_{\text{or}}^{{\text{max}}} }}{{S_{\text{oi}}^{{\text{max}}} }} $$

(11)

where $S_{\text{or}}^{{\text{max}}}$ is the maximum residual oil saturation and $S_{\text{oi}}^{{\text{max}}}$ is the maximum the initial oil saturation.

The water relative permeability is expressed by equations as follows:

$$ k_{\text{rw}}^{\text{Dr}} \left( {S_{\text{w}} } \right) = k_{\text{rw}}^{\text{Dr}} \left( {S_{\text{wc}} } \right)\,*\,\left( {\frac{{S_{\text{w}} - S_{\text{wc}} }}{{1 - S_{\text{wc}} }}} \right)^{{n_{\text{wd}} }} $$

(12)

$$ k_{\text{rw}}^{{{\text{Im}}\,b}} \left( {S_{\text{w}} } \right) = k_{\text{rw}}^{\text{Dr}} \left[ {S_{\text{oi}} } \right] \times \left[ {\frac{{S_{\text{w}} - S_{\text{wx}} }}{{1 - S_{\text{wx}} - S_{\text{or}} \left( {S_{\text{oi}} } \right)}}} \right]^{{n_{\text{wi}} }} $$

(13)

where $k_{\text{rw}} \left[ {S_{\text{or}} \left( {S_{\text{oi}} } \right)} \right]$ is the water relative permeability at $S_{\text{or}} \left( {S_{\text{oi}} } \right)$ and is given by:

$$ k_{\text{rw}}^{\text{Im}} \left[ {S_{\text{or}} \left( {S_{\text{oi}} } \right)} \right] = 1 - S_{\text{or}} \left( {S_{\text{oi}} } \right) \times \left[ {\frac{{1 - k_{\text{rw}}^{\text{Im}} \left( {S_{\text{or}}^{{\text{max}}} } \right)}}{{S_{\text{or}}^{{\text{max}}} }}} \right] $$

(14)

And S_wx is obtained by the below equation:

$$ S_{\text{wx}} = \frac{{S_{\text{wi}} - \left[ {1 - S_{\text{or}} \left( {S_{\text{oi}} } \right)} \right] \times \left\{ {\frac{{k_{\text{rw}}^{\text{Dr}} \left( {S_{\text{wi}} } \right)}}{{k_{\text{rw}}^{\text{Im}} \left[ {S_{\text{or}} \left( {S_{\text{oi}} } \right)} \right]}}} \right\}^{{\left( {\frac{1}{{n_{\text{wi}} }}} \right)}} }}{{1 - \left\{ {\frac{{k_{\text{rw}}^{\text{Dr}} \left( {S_{\text{wi}} } \right)}}{{k_{\text{rw}}^{\text{Im}} \left[ {S_{\text{or}} \left( {S_{\text{oi}} } \right)} \right]}}} \right\}^{{\left( {\frac{1}{{n_{\text{wi}} }}} \right)}} }} $$

(15)

$S_{\text{wx}}$ is a mathematical solution to ensure that the water imbibition scanning relative permeability curve and bounding drainage relative permeability curve $k_{\text{rw}}^{\text{Dr}} \left( {S_{\text{w}} } \right)$ are equal at the initial water saturation, $S_{\text{wi}}$.

The Nono et al. (2014) hysteresis model

For water branch scanning curve, Nono et al. (2014) used the following equation:

$$ K_{\text{rw}}^{\text{Im}} (S_{\text{o}} ) = K_{\text{rw}}^{\text{Dr,Exp}} (S_{\text{o}}^{\text{Hyst}} ) + \left[ {\frac{{K_{\text{rw}}^{\text{Im,Exp}} (S_{\text{o}}^{\text{norm}} ) - K_{\text{rw}}^{\text{Im,Exp}} (S_{\text{o}}^{\text{norm}} )}}{{K_{\text{rw}}^{\text{Im,Exp}} (S_{\text{orw}}^{{\text{max}}} ) - K_{\text{rw}}^{\text{Dr,Exp}} (S_{\text{orw}}^{{\text{max}}} )}}} \right] \times \left[ {K_{\text{rw}}^{\text{Im,Exp}} (S_{\text{orw}} ) - K_{\text{rw}}^{\text{Dr,Exp}} (S_{\text{o}}^{\text{Hyst}} )} \right] $$

(16)

where $K_{\text{rw}}^{\text{Dr,Exp}} (S_{\text{o}}^{\text{Hyst}} )$ is primary drainage K_rw at S ^Hyst_o , $K_{\text{rw}}^{\text{Im,Exp}}$ corresponds to the bounding imbibition K_rw, a combination of Killough’s and Skjaeveland’s approach of construction.

For oil branch scanning curve, a weighting scheme with saturation gap between the derived water-wet curve and the derived intermediate-wet curve is used to derive the scanning curve at S_oi as follows:

$$ K_{\text{row}}^{{\text{Im}}} (S_{\text{o}} ) = \left( {\frac{{S_{\text{o}}^{{\text{Max}}} - S_{\text{o}}^{\text{Hyst}} }}{{S_{\text{o}}^{{\text{Max}}} }}} \right) \times K_{{{\text{row,w{-}wet}}}}^{{\text{Im} , {\text{Derived}}}} (S_{\text{o}} ) + \left( {\frac{{S_{\text{o}}^{\text{Hyst}} }}{{S_{\text{o}}^{{\text{Max}}} }}} \right) \times K_{{{\text{row,int{-}wet}}}}^{\text{Dr,Exp}} (S_{\text{o}} ) $$

(17)

where $K_{{{\text{row,w{-}wet}}}}^{{\text{Im},{\text{Derived}}}} (S_{o} )$ is the scanning curve obtained by Killough’s model using primary drainage as a master curve and $K_{{{\text{row,int{-}wet}}}}^{{\text{Im},{\text{Exp}}}} (S_{\text{o}} )$ is the bounding imbibition curve departing from S_{oi, max} which is taken as intermediate-wet condition curve. $S_{\text{orw}}^{{\text{max}}}$ represents the residual oil saturation achieved for bounding imbibition curve.

Results and discussion

Analysis of pore throat mode

By identifying the maximum pore throat size with the known minimum entry pressure (P_d), the results of 150 MICP curves matching have been shown in Fig. 4. It is clear from Fig. 4 that most of the capillary entry pressures lie in the range of 100–400 psi and pore throat diameter ranges from 0.8 to 2.0 µm for the majority of the core plugs. It should be mentioned that some of the core plugs show very ‘tight’ property as the maximum pore throat diameter is smaller than 0.8 µm as shown in Fig. 4 (right). Results depicted in Fig. 5 show modality of the maximum pore throat diameter. The peak of maximum pore throat is about 1 µm which carries most of the porosity in pore system. The maximum pore throat diameter, i.e., 10 µm has a low-frequency distribution in these measured core plugs indicating the ‘tight’ property of this carbonate reservoir.

Fig. 4

Frequency of occurrence of all P_d values for Thomeer matching, indicating the maximum pore throat distribution in all core plugs (left), and derived maximum pore-throat diameter (µm) (right)

Fig. 5

Histograms of pore-throat diameter from MICP data (Black dots) along with pore-throat histograms from Thomeer hyperbola (read line); it shows a typical unimodal pore system (left), and a typical bimodal pore system (right)

Rock-type identification

The derived water saturation (S_w) log for all the 150 MICP curves is shown in Fig. 6. The S_w is derived from the buoyancy model, which assumes that at a certain depth above free water level (FWL), the buoyancy pressure (P_b) between water and oil is in an equilibrium state with the capillary pressure P_cwo. The buoyancy pressure and capillary pressure of oil and water in the reservoir have been expressed by the following equations:

$$ P_{\text{b}} = (\rho_{{{\text{w}}_{\text{reservoir}} }} - \rho_{{{\text{o}}_{\text{reservoir}} }} )gH $$

(18)

$$ P_{{{\text{cwo}}_{\text{reservoir}} }} = \frac{{P_{\text{cHgair}} \sigma_{{{\text{cwo}}_{\text{reservoir}} }} \cos (\theta_{{{\text{cwo}}_{\text{reservoir}} }} )}}{{\sigma_{\text{cHgair}} \cos (\theta_{\text{cHgair}} )}} $$

(19)

where $\Delta \rho$ is the density difference between water and oil, g is the gravity of acceleration, and H represents the height above free water level (HAFWL). In Eq. 19, σ signifies the interfacial tension (IFT), and θ indicates the contact angle obtained from laboratory measurements. Using standard values of these parameters, the equation is validated and converted to the following:

$$ P_{{{\text{cwo}}_{\text{reservoir}} }} = P_{\text{cHgair}} \times 0.1124 $$

(20)

Fig. 6

Water saturation derived from MICP data (black-dotted) using buoyancy model and log-based water saturation (blue line)

Figure 6 shows a good correlation between the MICP-derived water saturation and the log-based water saturation values. Meanwhile, the core plug samples capture some S_w characteristics that are not observed in log S_w.

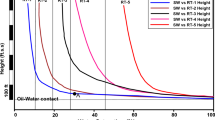
After determining the rock types (RT), the variance between water saturation S_w derived from RTs and S_w log data versus rock types has been plotted in Fig. 7. From Fig. 7, it has been observed that as the number of RTs increases the variance decreases. However, the variance shows very little change for five RT’s and above. Hence, with the purpose of describing the heterogeneity and minimizing the number of RTs in the dynamic model, the optimum number of rock types has been selected as five. The resulting five RTs are then used to derive the water saturation and compared with log S_w data. It has been found from Fig. 8 that 5 RTs still follow the log S_w trend although some detailed information is missing due to clustering. After the grouping of samples into rock types, it was decided to overlay the rock types on a porosity–permeability scatter plot as shown in Fig. 9 to observe whether any correlation exists between the rock types and the joint distribution of these petrophysical properties.

Fig. 7

Plot of variance between water saturation S_w derived from RTs and S_w log data and numbers of rock types

Fig. 8

Capillary pressure for the five RTs

Fig. 9

Rock typing result illustration in porosity Φ versus permeability k_air domain shows the petrophysical property difference of different rock types

It has been seen that different pore systems of rock types can produce similar porosities and permeabilities. But the present study is still able to distinguish the rock types with separation in the porosity–permeability domain. This leads to a conclusive remark that the petrophysical rock typing techniques based on porosity and permeability alone may have low resolution in classifying cores with different pore systems whereas grouping rocks based on their pore system features can help avoid this misleading issue.

Dynamic modeling

Generating scanning curves for dynamic modeling

Oil–water relative permeability correlations are critically important for transition zone modeling. Several hysteresis models are available in the industry, but mostly failed to describe the mixed-wet property and complex S_oi versus S_or relationship in the transition zone. In this study, two up-to-date hysteresis models by Masalmeh et al. (2007) and Nono et al. (2014), suitable for the mix-wet condition, are applied to perform dynamic modeling of the transition zone.

To generate a full set of bounding and scanning relative permeability curves, the following parameters are required to be defined for each S_oi value at the given HAFWL:

• (a) The residual oil saturation as a function of the initial oil saturation, f(S_oi).

This relationship can be determined experimentally. The S_oi/S_or relationship model includes Land’s type, Suzanne type (plateau type), and Linear correlation type. It needs to be determined by special core analysis (SCAL) data.

The Land’s type relationship with scaling parameter (c) is given as follows:

$$ \frac{1}{{S_{\text{or}} (S_{\text{oi}} )}} - \frac{1}{{S_{\text{oi}} }} = c $$

(21)

The Suzanne type (plateau type) relationship is:

$$ \begin{aligned} S_{\text{or}} (S_{\text{oi}} ) & = S_{\text{or}}^{{\text{max}}} \quad S_{\text{oi}} \ge S_{\text{oi}} c \\ S_{\text{or}} (S_{\text{oi}} ) & = \frac{{S_{\text{oi}} \times S_{\text{or}}^{{\text{max}}} }}{{S_{\text{oi}} c}}\quad S_{\text{oi}} < S_{\text{oi}} c \\ \end{aligned} $$

(22)

S_oic is the maximum the initial oil saturation above which there is no dependency of S_oi/S_or.

The Linear-type relationship is:

$$ S_{\text{or}} (S_{\text{oi}} ) = \frac{{S_{\text{oi}} \times S_{\text{or}}^{{\text{max}}} }}{{S_{\text{oi}}^{{\text{max}}} }} $$

(23)

As seen from Fig. 10, linear relationship between S_oi and S_or exists in the experimental data.

• (b) The bounding drainage and imbibition oil/water relative permeability curves.

Fig. 10

Initial oil saturation (S_oi) versus residual oil saturation (S_or), results for steady-state imbibition experiments

These experimental data should be matched using the relative permeability model in advance. Corey and Lomeland–Ebeltoft–Thomas (LET) equation is available in the program mentioned below (Corey 1954; Lomeland et al. 2005). The Corey equation is most widely used for K_r versus S_w relationship. The LET equation is recently developed and can describe K_r versus S_w relationship more precisely with three tuning parameters for oil and water as depicted in Table 1. From Fig. 11, it is observed that the LET equation matched with the drainage relative permeability curve of core No. 22 more accurately compared with Corey model.

Table 1 Matching parameters for the well in steady-state drainage/imbibition experiment data

Fig. 11

Drainage K_r curve matching using Corey and LET method, the LET method matches with experiment data much better than Corey method

Corey model is given as follows:

$$ k_{\text{rw}} = k_{\text{rw}} \left( {S_{\text{wn}} } \right)^{\text{nw}} ;\quad k_{\text{ro}} = k_{\text{ro}} \left( {1 - S_{\text{wn}} } \right)^{\text{no}} $$

(24)

$$ S_{\text{wn}} (S_{\text{w}} ) = \frac{{S_{\text{w}} - S_{\text{wir}} }}{{1 - S_{\text{wir}} - S_{\text{orw}} }} $$

(25)

Lomeland–Ebeltoft–Thomas (LET) model is presented below:

$$ k_{\text{rw}} (S_{\text{w}} ) = \frac{{(k_{\text{rw}} )_{{S_{\text{wi}} }} \times S_{\text{wn}}^{{L_{\text{w}} }} }}{{S_{\text{wn}}^{{L_{\text{w}} }} + E_{\text{w}} \times (1 - S_{\text{wn}} (S_{\text{w}} ))^{{T_{\text{w}} }} }} $$

(26)

$$ k_{\text{row}} (S_{\text{w}} ) = \frac{{(k_{\text{ro}} )_{{S_{\text{orw}} }} \times (1 - S_{\text{wn}} (S_{\text{w}} ))^{{L_{\text{o}} }} }}{{(1 - S_{\text{wn}} (S_{\text{w}} ))^{{L_{\text{o}} }} + E_{\text{o}} \times (S_{\text{wn}} (S_{\text{w}} ))^{{T_{\text{o}} }} }} $$

(27)

$$ S_{\text{wn}} (S_{\text{w}} ) = \frac{{S_{\text{w}} - S_{\text{wir}} }}{{1 - S_{\text{wir}} - S_{\text{orw}} }} $$

(28)

• (c) As mentioned previously, the Killough hysteresis model, Masalameh model (2007, modified from Corey model), and Nono et al. (2014) model are used in the present work for comparison purpose.

Figure 10 shows the initial oil saturation (S_oi) versus residual oil saturation (S_or) relationship from the well for steady-state imbibition experiments, it is seen that S_or is about 0.1 when S_oi is larger than 0.25; Plug 113, 114,138 and 139 show higher S_or values. This may be due to the effect of pore geometry. The experimental results show a plateau-type relationship between S_oi and S_or; hence, a plateau type model is used to generate scanning curve in the program. Figure 12 shows the interface used to generate the relative permeability scanning curves for each of the five rock types.

Fig. 12

Relative permeability scanning curves generation interface

Figures 13, 14, 15, 16, and 17 show the relative permeability curves and generate scanning curves for different rock types. The used drainage and imbibition curves for the cores have been depicted in Table 2. Different sets of the initial water saturation scanning values for the same bounding curve per rock type were tested and scanning curves were generated at an interval of 0.05% change in S_w. Finally, 59 scanning curves were generated and input into the simulation model.

Fig. 13

Bounding drainage/imbibition curve and scanning curve for rock type 1(Masalmeh Model, linear-type S_oi/S_or relationship)

Fig. 14

Bounding drainage/imbibition curve and scanning curve for rock type 2 (Masalmeh model, linear-type S_oi/S_or relationship)

Fig. 15

Bounding drainage/imbibition curve and scanning curve for rock type 3 (Masalmeh model, linear-type S_oi/S_or relationship)

Fig. 16

Bounding drainage/imbibition curve and scanning curve for rock type 4 (Masalmeh model, linear-type S_oi/S_or relationship)

Fig. 17

Bounding drainage/imbibition curve and scanning curve for rock type 5 (Masalmeh model, linear-type S_oi/S_or relationship)

Table 2 Drainage/imbibition relative permeability curves used in this study

Single well model

Petrophysical properties of the reservoir obtained from well log data and CCA, SCAL experiments of the 64 plugs, were incorporated to generate a single well model. This model was then used to run the simulation to predict the transition zone performance. Layering for this model was done by creating surfaces between each of the sampled plugs (Fig. 18). Three petrophysical models—porosity, permeability, and water saturation were built for this well with the help of core data. Figures 19 and 20 show the porosity and water saturation distribution of the single well model. These models were then used as inputs for a simulation run. Additionally, rock types were assigned to each layer using Thomeer’s Method. This would be useful in assigning the capillary pressure and relative permeability curves to each layer during simulation.

Fig. 18

Single well model showing different layering thickness

Fig. 19

Single well model showing porosity property

Fig. 20

Single well model showing water saturation (derived from MICP data)

The simulation was run with and without hysteresis for a mixed-wet reservoir to see the effect and importance of incorporation of hysteresis model for transition zone reservoir modeling and simulation with this single well model showed overestimated oil production with lower water cut when running without hysteresis. To overcome the problem, it is important to use hysteresis in the dynamic model for transition zone simulation.

Production performance in transition zone

Many experiments performed on core plugs from carbonate reservoir transition zone demonstrate that a mixed-wet condition widely exists in the transition zone. The mixed-wet formation will lead to different recovery mechanisms compared to that in a normal water-wet formation. However, in the industry, the mixed-wet condition and relative permeability hysteresis phenomenon are often ignored when performing transition zone simulation runs. In this work, an attempt has been taken to incorporate relative permeability hysteresis under mixed-wet condition into simulation runs for better understanding the production performance of a transition zone. The most widely used commercial simulation software does not have any built-in hysteresis model designed for the mixed-wet condition. Hence, alternatively, the scanning curves are generated by the mixed-wet Masalameh relative permeability correlation in an independent software (Masalmeh et al. 2007), and input into the simulation runs manually.

In Fig. 21, the water cut and recovery factor are compared for different simulation scenarios. As production continues, the water cut gradually increases with time and production rate declines. With the elapse of time, recovery factor increases. It is noticeable that the oil production from transition zones is considerable.

Fig. 21

Comparison of water cut and oil rate for different simulation runs with and without hysteresis

However, the simulation running with mixed-wet condition shows a higher water cut compared with the simulation with no hysteresis model. As the formation changes from water-wet to mixed-wet, the water relative permeability increases. This is important because ignoring the mixed-wet condition when running a simulation for economic evaluation purposes may lead to higher oil estimation, and delayed water breakthrough time, which is an opposite condition to reality.

Conclusion

Rock typing and relative permeability correlations are critically important for understanding and dynamic modeling of the transition zone. The present study has taken an attempt to produce a complete model and simulation for transition zone. Further study on the relative permeability hysteresis in transition zone should be carried out in the future. Based on the generated results, the following conclusions can be made:

• 1. The Thomeer hyperboles method is successfully applied to decode the pore system of carbonate reservoir rock samples in the Middle East region, based on 150 MICP curves.

• 2. An execution program is developed to generate scanning curves for transition zone simulation. This program includes the most up-to-date relative permeability correlation. Different S_oi and S_or relationship models are also included in the program. It is helpful for simulation runs of different wettability cases.

• 3. The S_oi/S_or correlation strongly depends on wettability, pore structure, and pore-size distributions. Land’s correlation may not be valid for oil-wet carbonates because it was derived on the basis of a water-wet assumption. Extensive experimental measurements using representative rock/fluid systems are required to establish this correlation. From the steady-state imbibition experiments of core plugs of the well, a linear-type relationship between S_oi and S_or is observed.

• 4. In capillary transition zones, it is very important to use the correct hysteresis model to do performance prediction. The conventional no hysteresis-included simulation may lead to inaccurate higher oil production estimation.