Introduction

Crude oil viscosity is an important physical property that controls and influences the flow of oil through porous media and pipelines. The viscosity, in general, is defined as the internal resistance of a fluid to flow. Oil viscosity is a strong function of many thermodynamic and physical properties such as pressure, temperature, solution gas–oil ratio (GOR), bubble point pressure, gas gravity, and oil gravity. Viscosity of crude oil is a fundamental factor in simulating reservoirs, forecasting production as well as planning thermal enhanced oil recovery methods that make its accurate determination necessary.

Usually oil viscosity is determined by laboratory measurements at reservoir temperature. However, experimental determination of reservoir oil viscosity is costly and time-consuming. A literature survey has indicated that empirical viscosity correlations developed are divided into three major types: dead oil viscosity, saturated oil viscosity, and undersaturated oil viscosity. Figure 1 shows a typical oil viscosity diagram as a function of pressure at constant reservoir temperature.

Fig. 1
figure 1

Typical viscosity trend as a function of pressure

Full size image

Saturated oil viscosity

Numerous correlations have been proposed to calculate the oil viscosity. These correlations predict viscosities from available field-measured variables including reservoir temperature, oil API gravity, solution gas–oil ratio, pressure, and saturation pressure.

Chew and Connally (1958) presented their crude viscosity correlation as a function of dead oil viscosity and solution gas–oil ratio under reservoir conditions. Viscosity was measured for data of 457 crude oil samples gathered from different areas of USA, Canada, and South America. Measurements were conducted within the ranges of 72–292 °F, 132–5645 psia, and 51–3544 cu ft/bbl for reservoir temperature, bubble point pressure, and solution gas–oil ratio at bubble point, respectively.

Beggs and Robinson (1975) developed fairly accurate and simple crude oil viscosity model based on API gravity temperature and solution gas–oil ratio. Measurements of 600 samples dataset were used to derive the correlation with pressure range of 0.0–5250 psig, solution GOR of 20–2070 scf/STB, oil gravity of 16–58 °API, and temperature of 70–295 °F. They limit their correlation on data that do not have crude composition and suggest using different correlations for better accuracy if composition is available.

Later, Khan et al. (1987) published their empirical correlation using Saudi Arabian crude oil viscosity measured using rolling ball viscometer at various pressures and temperatures. The study utilized viscosity data of 75 bottom-hole samples taken from 62 Saudi oil reservoirs. A total of 1691 data measurements below the bubble point pressure were used to derive the correlation which is simply based on crude bubble point viscosity, pressure, and bubble point pressure. They compared their model with Begs and Robinson and Chew and Connally and claimed that their own correlation was the most accurate for Saudi crudes.

Naseri et al. (2005) used PVT experimental data of 472 series of Iranian oil reservoirs in developing their empirical correlation. These data include oil API gravity, reservoir temperature, saturation pressure, solution gas–oil ratio, and PVT measurements at reservoir temperature. Out of the total dataset, 250 were used to develop the empirical model and the rest was spared for validation purposes. Dead viscosity and bubble point pressure were used as input parameter and model developed was of good accuracy exceeding that of the models they compared with average absolute error of 26.31%.

Undersaturated oil viscosity

Many correlations have been proposed to calculate the undersaturated oil viscosity. These correlations predict viscosities from available field samples including reservoir temperature, oil API gravity, solution gas–oil ratio, pressure, and saturation pressure. Vazquez and Beggs (1977) used more than 600 laboratory PVT analyses from fields of different geographical locations. The data encompassed very wide ranges of pressure, temperature, and oil properties and included more than 6000 measurements of gas solubility, oil formations volume factor, and oil viscosity at various pressures. Regression analysis techniques were used to correlate the laboratory data.

Khan et al. (1987) utilized viscosity data of 75 bottom-hole samples taken from 62 Saudi oil reservoirs. A total of 1503 data measurements above the bubble point pressure were used to derive the correlation which is simply based on crude bubble point viscosity, pressure, and bubble point pressure. They compared their model with Beal’s (1946) correlation, and it gives close estimates for undersaturated crude oil viscosity.

Kartoatmodjo and Schmidt (1991) used widespread data collected from PVT reports and literature. A set of 5392 data points was used to develop their correlation. These data represent 740 different crude oil samples. For the development of undersaturated oil properties correlations, a total of 3588 data points collected from 661 different crude oil samples were used. The functional form of Sutton’s was used in this study to develop the undersaturated oil viscosity correlation. They developed a crude oil viscosity model based on API gravity, temperature, and solution gas–oil ratio. The used data have the following ranges: oil gravity of 14.4–59 °API, pressure of 14.7–6054.7 psia, temperature of 75–320 °F, and solution–gas ratio of 0–2890 scf/stb.

Hossain et al. (2005) presented their empirical correlations for dead, saturated, and undersaturated heavy oil utilizing three databanks. The databanks consist of heavy oil data from various parts of the world with wide ranges of temperature, pressure, and fluid compositions. A total of 361 data points were used to develop the undersaturated oil viscosity correlation. With temperature range of 118–218.7 °F, solution–gas ratio of 19.4–493 scf/bbl, bubble point pressure of 121–6272 psia, and pressure of 300–6400 psia.

Bergman and Sutton (2006) developed their correlation which provides a wider range of bubble point viscosity and pressure differentials than other existing correlations for undersaturated oil viscosity. This model derives undersaturated viscosity using only bubble point viscosity and pressure differential. The correlation can be satisfactorily used on gas free oils and oil with solution gas. The data used to derive the correlation included samples with bubble point viscosity from less than 0.1–14,000 cp. Accuracy is maintained over this wide range of values.

Genetic programming

Genetic programming (GP) is a development in the field of evolutionary algorithms extending the classical genetic algorithms (GA) to a symbolic optimization technique and overcoming GA limitation of being a fixed-length representation scheme requiring encoding of the variables and its non-dynamic variability requiring the string length to be defined in advance (Koza 1992). Unlike common optimization methods, GP is able to work with a coding of the design variables as opposed to the design variables themselves. It is a problem-independent application working with a population of points as opposed to a single point. In addition, it requires the objective function value only, not the derivatives. Finally, GP is considered highly exploitative family of probabilistic (non-deterministic) search approach (Alvarez 2000).

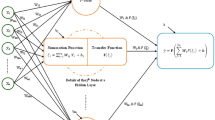
GP is based on so-called tree representation in which trees can represent computer programs, mathematical equations, or complete models of process systems. GP initially creates an initial population generating random individuals (trees) of functions and terminals (inputs) to represent the problem. In all iterations, the algorithm executes and evaluates the individuals in the population and assigns a fitness value. Individuals are then selected for reproduction and generate new individuals by mutation, crossover. Finally, the best program in the generation is designated (Koza 1992). Figure 2 shows a flowchart presenting general genetic programming workflow.

Fig. 2
figure 2

General flowchart of genetic programming (Koza et al. 2003)

Full size image

The generated potential solutions in the form of a tree structure during the GP operation may have better and worse terms (subtrees) that contribute more or less to the accuracy of the model represented by the tree structure. Orthogonal least squares (OLS) algorithm is used to estimate the contribution of the tree branches to the accuracy of the model, and hence, terms having the smallest error reduction ratio could be eliminated from the tree. Figure 2 illustrates an example of elimination of a sub-tree based on OLS.

Results and discussion

A database of 150 Saudi Arabian crude oil samples was utilized. The database includes 79 saturated samples and 71 undersaturated samples with viscosity measurements (µ) at wide ranges of pressures and temperatures. Other parameters including dead oil viscosity (µ d), solution gas–oil ratio (R s), bubble point pressure (P ob), crude API, gas specific gravity (γ g), and crude viscosity at bubble point (µob) are also included. The quality of the data was judged and compared before they were considered and they were randomized and used in genetic programming (GP) software capable of building computer program out of the data provided to develop, test and validate the two proposed saturated and undersaturated viscosity models. Both saturated and undersaturated datasets were divided into three segments. The first two were used to train and test the model while the third was spared to blind test and validate the model efficiency. The software was run for 1000 generations with a maximum population size of 500. Several values of crossover and mutation rates were investigated, and the optimum setting found was 50 and 95% for crossover frequency and mutation frequency, respectively. The function set used was limited to (+, −, *, / and √) while the terminal set was the input parameters for each model in addition to machine randomly generated constants. The generation of genetic programming models was started and terminated when project history showed no improvement (Fig. 3).

Fig. 3
figure 3

An example of elimination of a sub-tree

Full size image

Saturated oil viscosity model

A dataset of 79 saturated crude samples was randomized, and two segments of 26 samples each were used for both training and testing. The rest was used for model validation and blind testing. The model was simply developed as a function of solution gas–oil ratio and viscosity at bubble point pressure as input parameters. The evolved viscosity model shows efficient performance, and Table 1 lists the domain of the data segments used in building and testing processes in addition to that used for validation of the developed GP saturated oil viscosity model. Figure 4 presents the best evolved genetic program in C++ code. The f[0], f[1], etc. are temporary computation variables used in the program evolved. The output is the value of f[0] after program execution. The variable labels V[0], V[1], etc. are the names assigned to input data. Writing up the equation (Eq. 1) representing the evolved program for saturated oil viscosity, we obtained the following:

$$\mu = \frac{{a_{15} \left[ {\left( {D + \frac{{\left| {2D} \right| - D}}{{a_{16}^{2} }}} \right)\left( {a_{16}^{2} - a_{16} } \right) - \frac{{\left| {2D} \right| - D}}{{a_{16}^{2} }}} \right] + a_{16}^{3} \mu_{d} }}{{a_{16}^{4} }}$$
(1)

where

$$D = \left| {\frac{{a_{13} C - 2A + a_{14} }}{B}} \right| + 7\left( {\frac{2A}{B} - a_{2} } \right)$$
$$A = R_{s} \left( {a_{1} - \mu_{d}^{2} } \right) - a_{2}$$
$$B = \frac{{a_{4} A^{2} \left( {2 - a_{5} \mu_{d} } \right)^{2} }}{{a_{3} }} + a_{6} \mu_{d} + a_{7}$$
$$C = \sqrt {\left| {a_{10} \mu_{d} + a_{11} \mu_{d} R_{s} + a_{12} } \right|}$$
Table 1 Minimum and maximum values for the used data in building and validating the new saturated crude viscosity model
Full size table
Fig. 4
figure 4figure 4

Saturated crude viscosity model in C++ language

Full size image

The A, B, C, and D are the computation variables used in the program evolved, whereas the a1, a2, … a16 are the correlation coefficients as listed.

a1

1.9244

a9

0.9592

a2

0.0026

a10

0.6221

a3

0.6189

a11

0.0023

a4

2.8541

a12

0.1979

a5

0.9404

a13

0.6342

a6

1.0895

a14

0.6617

a7

1.4270

a15

1.3709

a8

1.0632

a16

0.9974

The model efficiency was compared to some published correlations such as Chew and Connally (1958), Beggs and Robinson (1975), Khan et al. (1987), and Naseri et al. (2005). Figure 5 consists of crossplots of the predicted versus experimentally measured viscosities using the developed genetic viscosity model and the four previously mentioned correlations. Average absolute relative error (AARE) and Pearson’s coefficient of correlation (COC) defined in Eqs. 2 and 3 were calculated, and the AARE was used to validate the efficiency of proposed model in comparison with other tested models.

$$AARE = \frac{100}{n}\sum {\frac{{\left| {\mu_{Actual} - \mu_{Forecast} } \right|}}{{\left| {\mu_{Actual} } \right|}}}$$
(2)
$$COC = \frac{{\sum {\left( {\mu_{Actual} - \overline{{\mu_{Actual} }} } \right)\left( {\mu_{Forecast} - \overline{{\mu_{Forecast} }} } \right)} }}{{\sqrt {\sum {\left( {\mu_{Actual} - \overline{{\mu_{Actual} }} } \right)^{2} \left( {\mu_{Forecast} - \overline{{\mu_{Forecast} }} } \right)^{2} } } }}$$
(3)

where

  • \(\mu_{Actual}\)  = measured viscosity value, cp.

  • \(\mu_{Forecast}\) = correlated viscosity value, cp.

  • \(\overline{{\mu_{Actual} }}\) = average measured viscosity value, cp.

  • \(\overline{{\mu_{Forecast} }}\) = average correlated viscosity value, cp.

Fig. 5
figure 5

Predicted versus experimentally measured saturated oil viscosity

Full size image

The figure indicates that the proposed model (Fig. 5a) outperforms the other correlations in predicting the experimentally measured viscosity with the least average absolute relative error (AARE) of 9.37% and highest coefficient of correlation (COC) of 99.35%. Beggs and Robinson (1975) was the second best correlation while the least accuracy was that of Naseri et al. (2005). Khan et al. (1987) correlation was originally developed for Saudi crude oil, and we expected high performance; however, it shows a significant departure from the 45° line for higher viscosity range of our dataset. Table 2 summarizes the accuracy of the developed GP model in comparison with the different correlations in predicting the saturated crude oil viscosity.

Table 2 Accuracy of developed saturated crude oil viscosity model in comparison with different published correlation
Full size table

Undersaturated oil viscosity model

The dataset used for this model consists of 71 experimental measurements of undersaturated crude oil viscosity. The model was developed as a function of pressure, bubble point pressure, and viscosity at bubble point pressure as input parameters. Table 3 lists the ranges of the data used in building and validating the new undersaturated oil viscosity model constituting the limits of the model. Figure 6 presents the best evolved genetic program in C++ code. Equation 4 represents the write up of the evolved program for undersaturated oil viscosity,

Table 3 Minimum and maximum values for the used data in building and validating the new undersaturated crude viscosity model
Full size table
Fig. 6
figure 6

Undersaturated crude viscosity model in C++ language

Full size image
$$\mu = \mu_{ob} + b_{8} *D - b_{9} .$$
(4)

where

$$D = b_{6} (C - \mu_{ob} ) - b_{7}$$
$$C = \left( {\frac{P}{{P_{b} }}} \right)\left( {b_{4} \cdot A \cdot B + b_{5} + \mu_{ob} } \right)$$
$$B = \mu_{ob} - b_{3}$$
$$A = b_{1} \left( {\frac{P}{{P_{b} }}} \right)\left( {\mu_{ob} - b_{2} } \right)$$

Again, the A, B, C, and D are the computation variables used in the evolved program, whereas the b1, b2, … b9 are the correlation coefficients listed as follows:

b1

0.1317

b4

1.0529

b7

0.0086

b2

1.7892

b5

0.3579

b8

0.3055

b3

3.4466

b6

0.1323

b9

0.0099

The model efficiency was tested against some commonly used correlations such as Vazquez and Beggs (1977), Khan et al. (1987), Kartoatmodjo and Schmidt (1991), Hossain et al. (2005), and Bergman and Sutton (2006). The evolved undersaturated viscosity GP model shows efficient performance over wide ranges of input variables. Figure 7 consists of plots of the predicted versus experimentally measured viscosities using the developed genetic viscosity model and the four previously mentioned correlations. All models tested shows good accuracy with best performance obtained with the proposed GP model indicating an average absolute relative error of 9.36%. Table 4 shows the accuracy of the developed model in comparison with the different correlations in predicting the undersaturated crude oil viscosity.

Fig. 7
figure 7

Predectied versus experimentally measured undersaturated oil viscosity

Full size image
Table 4 Accuracy of developed model in comparison with different methods in predicting the undersaturated crude oil viscosity
Full size table

Sensitivity analysis

The impacts of the input independent variables on saturated and undersaturated crude oil viscosity models were calculated and presented by the GP software. The purpose of variable impact analysis is to measure the sensitivity of model predictions to changes in independent variables. As a result of the analysis, every independent variable is assigned a relative variable impact value. The lower the percent value for a given variable, the less that variable affects the prediction. The results of the analysis can help in testing the model results robustness and simplifying the model with adequate accuracy by reducing the number of independent variables (inputs), those that have very low impact, if many were involved (AlQuraishi 2009). Figures 8 and 9 present the impact analysis of independent variables on saturated and undersaturated crude viscosity predictions, respectively. Saturated viscosity model is closely dependent on both R s and µ ob while undersaturated viscosity model is highly dependent on µ ob. The figures show the negative impact of RS and the positive impact of µ ob on saturated crude viscosity and the high positive impact of µ ob on undersaturated crude viscosity.

Fig. 8
figure 8

Sensitivity analysis of the saturated crude viscosity model

Full size image
Fig. 9
figure 9

Sensitivity analysis of the undersaturated crude viscosity model

Full size image

Conclusion

Two models were developed to estimate saturated and undersaturated crude oil viscosity. Genetic programming approach was used to develop these two models using experimental measurements. The models efficiency was tested against som commonly used correlations, and based on the results obtained, the following are concluded:

  • Saturated viscosity model developed using solution gas–oil ratio (R s) and dead crude viscosity (µ d) as input variables provided good accuracy in predicting the experimental measurements and outperforms the other tested correlations with AARE of 9.37%.

  • Undersaturated viscosity model developed using reservoir pressure (P) and crude bubble point pressure (P ob) and crude viscosity at bubble point pressure (µ ob) as inputs provided good accuracy in predicting the experimental measurements and outperforms the other tested correlations with AARE of 1.64%.

  • The developed saturated model sensitivity analysis indicates the equivalent impact of dead crude viscosity (µ d) and solution gas–oil ratio (R s) but in opposite trend.

  • The developed undersaturated model sensitivity analysis indicates the high positive impact of crude viscosity at bubble point (µ ob) and small negative impact of bubble point pressure (P ob) and trivial positive impact of reservoir pressure (P).