Introduction

Currently, reagent treatment of the fluid flow is widely used in the wastewater treatment technology, in particular, using reagent coagulation of colloidal and fine impurities (Adelshin and Potekhin 1997).

In the process of reagent coagulation, a quick and uniform distribution of coagulant reagents in the treated volume of wastewater is required to ensure the contact of the maximum amount of dispersed pollution particles with intermediate products of coagulant hydrolysis. Since the processes of the coagulant hydrolysis in the treated wastewaters are quite intensive, and intermediate hydrolysis products with increased activity exist for a short time, it becomes necessary to create such hydrodynamic conditions for mixing the wastewater volume, in which the coagulant reagent could interact with the maximum number of particles of impurities before the coagulant hydrolysis reaction will be completed. For mixing the volume of wastewater with reagents added to it, mechanical or hydraulic mixing devices are used. In these devices, there are an intensive equalization of concentrations contained in the treated fluid of the chemical ingredients, dispersion of emulsion droplets and solid particles of the suspension, and fragmentation of gas bubbles as a result of forced movement of the microvolumes of the mixing fluid.

Mechanical mixing devices are container structures (storage tanks). Mixing the volume of fluid in mechanical mixing devices is performed by mechanical agitators. Usually, there are bladed, turbine or propeller agitators mounted on a vertical shaft in mechanical mixing devices, which are driven by an electric motor (Adelshin and Potekhin 1997).

Hydraulic mixers, unlike mechanical ones, do not require the use of additional energy supplied to an electromechanical mixing device; they are distinguished by structural simplicity and operational reliability. In the hydraulic-type mixing devices, there is a principle of utilization of the own energy of the fluid flow due to its turbulization, which is created by local resistances or occurs as a result of an increase in the velocity of water motion (Adelshin and Potekhin 1997).

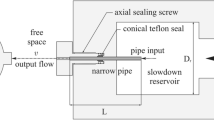
In technological processes of wastewater treatment, tubular hydrodynamic mixing devices (tubular mixers) are most widely used among hydraulic mixers, allowing to provide highly efficient mixing of treated water with reagents at the micro level (Adelshin and Potekhin 1997).

Tubular mixers have a developed contact surface of the fixed walls of the channel with a moving flow of treated wastewater, resulting in intensifying the process of microscale mixing that occurs in a thin wall layer of the flow. Mixing devices of this type are characterized by high productivity and intensity of mixing the treated volume of fluid, which leads to the possibility of their use in constraint environment. Tubular mixers are made in the form of structures assembled from pipes of the effective length and diameter.

This article considers theoretical aspects of fluid movement in a tubular mixer, which is a pressure channel of circular cross section. An analysis of hydrodynamic characteristics of the wall region of the flow was carried out, and mathematical relations, allowing us to optimize the operation regime of the tubular mixer, were obtained.

Experimental section

Theoretical background for calculating hydrodynamic characteristics of tubular mixing devices

According to the physical mechanism, there are two main types of mixing the volume of the treated fluid (Braginskiy et al. 1984):

  1. 1.

    Macroscale mixing is the process of averaging the characteristics of the treated fluid in local volumes, the dimension of which significantly exceeds the diameter of the droplets of emulsions and the particles of suspensions contained in the fluid.

  2. 2.

    Microscale mixing is the process of emerging shear forces in small elements of the treated fluid volume, comparable in dimension to the particles of the dispersed phase of the impurities contained in it.

Microscale mixing allows intensifying the processes in which equalization of concentrations of reacting substances at the macrolevel is not enough for normal chemical reactions, and a significant role is played by the advance or removal velocity of substances at the microlevel, up to the distances at which intermolecular forces interaction is manifested. Despite the fact that the transfer rate of substances in the volume elements of such a small scale is determined by molecular diffusion processes that depend on the temperature and physical properties of the medium and diffusing substances, the microscale structure of the flow can significantly influence it.

When conducting macroscale mixing in the treated volume of fluid, there is a uniform distribution not of the molecules of the reacting substances, but of the microvolumes of the fluid of different compositions. The dimension of these microvolumes can be negligible compared to the dimension of the total volume, in which the mixing process is carried out, but significantly exceeds the dimension of the molecules. Under such conditions, conventional measurement methods will fix the equality of local concentrations at all points of volume mixing. In reality, in this case there will be an extremely uneven distribution of the concentration of the reacting substances at the molecular level, which will significantly affect the course of chemical reactions.

The processes occurring in the mixing device can be divided into two groups:

  1. 1.

    Hydrodynamic transfer processes of dissolved substances and dispersed particles occurring under the influence of turbulent pulsations of the rates of fluid flow in the volume of the mixing device. In this case, the scale of the hydrodynamic pulsations of the fluid in the volume of the apparatus plays a significant role.

  2. 2.

    Hydrodynamic processes occurring at the phase boundary of fluid flow and a solid surface of the apparatus, or a surface of a mechanical agitator. At the same time, the characteristics of the thin boundary layer, which depend on the conditions of the flow of the mixed fluid in the immediate vicinity of surface of phase, have a major influence on the transfer rate of substances and the level of scale of this process.

Prandtl made the assumption that along with the laminar and turbulent regimes of fluid flow, there is another flow regime that has its own characteristic features. He wrote that “the movement of a fluid, in which the Reynolds number is less than unit, is called a creeping flow” (Prandtl 1942).

Analyzing the features of fluid movement in pressure channels, Landau concluded that a thin interlayer of fluid moving along it is adjacent to the channel wall, in which the magnitude of local Reynolds criterion is less than unity (Landau and Lifshitz 1987):

$$ \text{Re} = \frac{{\bar{u}_{\text{av }} y}}{\gamma } < 1 $$
(1)

where \( y \) is the distance from the channel wall to the flow point under consideration (m), ūav is the average value of the local flow velocity at the point under consideration (m/s) and γ is the kinematic viscosity coefficient m2/s.

The magnitude of the local velocity ūav in this interlayer varies from zero on the wall itself to the value of magnitude of the dynamic velocity υ* (m/s) according to the linear law. Landau wrote that “this interlayer is called a viscous sublayer” (Landau and Lifshitz 1987).

Thus, in the wall region of both laminar and turbulent flow, there is a thin interlayer of fluid moving along the walls, a “viscous sublayer,” in which a “creeping flow” regime is observed. At the same time, viscous friction forces acting on the stream filament exceed the inertial forces (Reδ< 1), the magnitude of the velocity gradient within the wall (viscous) sublayer has a constant value (\( G_{*} = \frac{{{\text{d}}u}}{{{\text{d}}y}} = {\text{const}} \)), and the value of the local velocity varies depending on the distance from the wall according to the linear law:

$$ u_{y} = G_{*} y\;\left( {\text{m/s}} \right). $$
(2)

At a distance of the wall layer thickness from the wall (y = δ*), the magnitude of the local flow velocity is equal to the magnitude of dynamic flow velocity (the velocity of the shear stress of the friction force)

$$ u_{*} = \upsilon_{*} = \upsilon \sqrt {\frac{{\tau_{*} }}{\rho }} = \sqrt {iRg} = \upsilon \sqrt {\frac{\lambda }{8}} \;\left( {\text{m/s}} \right), $$
(3)

where τ* is the magnitude of the shear stress of the friction force (N/m2); ρ is the density of the fluid (kg/m3); i is the hydraulic gradient; R is the hydraulic radius (m); g is the gravitational acceleration m/s2); υ is the average flow rate (m/s); and λ is the pipe friction factor (Darcy factor).

The symbol * indicates hereinafter that this characteristic belongs to the considered wall sublayer.

The velocity gradient G* will have the maximum value in the wall sublayer having a thickness of δ*.

In a pipe of circular cross section with a radius of r0 (m), the magnitude of the velocity gradient in the kernel of the fluid flow decreases according to the linear law with changing the distance from the flow axis r = r0–y:

$$ G_{r} = G_{*} \frac{{r_{0} - y}}{{r_{0} }} = G_{*} \frac{r}{{r_{0} }}\;({\text{s}}^{ - 1} ). $$
(4)

Under the laminar regime of fluid movement in a pipe of circular cross section, there is a parabolic law of changing the magnitude of local flow velocity ur along the current radius r, named after George Gabriel Stokes

$$ u_{r} = 2\upsilon \left[ {1 - \frac{{r^{2} }}{{r_{0}^{2} }}} \right]\; \left( {\text{m/s}} \right). $$
(5)

Differentiation of the Stokes Eq. (5) with regard to r = 2R (where R is the magnitude of the hydraulic radius) gives the formula:

$$ G_{r} = - \frac{{{\text{d}}u_{r} }}{{{\text{d}}r}} = \frac{4\upsilon }{{r_{0} }}\frac{r}{{r_{0} }} = \frac{2\upsilon }{R}\frac{r}{{r_{0} }}\; \left( {\text{m/s}} \right) $$
(5.1)

whence taking (4) into account

$$ G_{ * } = \frac{2\upsilon }{R}\; \left( {{\text{s}}^{ - 1} } \right). $$
(6)

From formula (2), if y = δ* and υav = υ* taking into account formulas (6) and (3), the thickness magnitude of the wall sublayer can be determined

$$ \delta_{ * } = \frac{{\upsilon_{ * } }}{{G_{ * } }} = R\frac{{\upsilon_{ * } }}{2\upsilon } = R\frac{{\upsilon \sqrt {\frac{\lambda }{8}} }}{2\upsilon } = R\sqrt {\frac{\lambda }{32}} \;({\text{m}}). $$
(7)

Formula (5) allows to obtain the value of the local velocity uδ*, the magnitude of which is different from the dynamic velocity value υ* (uδ* ≠ υ*), at a distance y = δ* from the flow wall. The intersection of the diagram of the real distribution of magnitudes of local velocities of laminar flow and the velocities diagram, constructed according to formula (5), is carried out at the boundary of the transition sublayer with the flow kernel.

The transition sublayer has a thickness δ**, equal to the thickness of the wall sublayer δ*.

The wall and transition sublayers together form a viscous layer having a thickness

$$ \delta = \delta_{*} + \delta_{**} = 2\delta_{*} \left( {\text{m}} \right). $$
(8)

In the case of a laminar regime of fluid movement, the magnitude of the pipe friction factor λ does not depend on the magnitude of the relative roughness of the flow channel \( \bar{\Delta } = \frac{\Delta }{d} \), defined as the ratio of the equivalent roughness Δ (m) (the average height of the projections of the flow channel) to the pipe diameter d (m), and is determined only by the value of the Reynolds criterion \( \text{Re} = \frac{\upsilon d}{\nu } \)

$$ \lambda = \frac{64}{\text{Re}}. $$
(9)

In accordance with formula (5), the magnitude of the local velocity on the flow axis at r = 0 reaches the maximum value

$$ u_{\hbox{max} \;L} = 2\upsilon \; \left( {\text{m/s}} \right). $$
(10)

The occurrence of turbulence in a fluid flow moving in a circular cross-section pipe leads to an increase in hydraulic resistance (the magnitude of the pipe friction factor λ) and a decrease in the magnitude of local average velocity on the flow axis (at r = 0) ūmaxT, which can be taken into account by introducing correction factors α and β in Eqs. (9) and (10), respectively

$$ \lambda = \frac{64}{\text{Re}}\,\alpha , $$
(11)
$$ \bar{u}_{\hbox{max} \;T} = 2\upsilon \beta \; \left( {\text{m/s}} \right). $$
(12)

Transforming formula (11), we get

$$ \lambda = \frac{64}{\text{Re}}\alpha = 64\frac{{\alpha {\kern 1pt} \nu }}{{\upsilon {\kern 1pt} d}} = 16\frac{{\alpha {\kern 1pt} \nu }}{{\upsilon {\kern 1pt} R}}\frac{\upsilon }{\upsilon }, $$
(13)

from which, taking into account formula (3), we have

$$ \frac{2\upsilon }{R} = \frac{\lambda }{8}\frac{{\upsilon^{2} }}{{\alpha {\kern 1pt} \nu }} = \frac{{\upsilon_{*}^{2} }}{\alpha \nu }. $$
(14)

Comparing formulas (14) and (6), we see that in the case of turbulent regime of fluid movement, the magnitude of the velocity gradient in the wall sublayer G* can be defined as

$$ G_{*} = \frac{2\upsilon }{R} = \frac{{\upsilon_{*}^{2} }}{\alpha \nu } = \frac{{\upsilon_{*}^{2} }}{{\nu_{*} }}\; \left( {{\text{s}}^{ - 1} } \right). $$
(15)

Analyzing formulas (11) and (15), it can be concluded that the coefficient α shows not only how many times the value of the pipe friction coefficient λ increases during the transition to the turbulent regime of fluid movement, but also how many times the value of the coefficient of kinematic viscosity ν in the wall sublayer increases.

Calculation of the Reynolds number at the critical transition point of the turbulent fluid flow to the region of the quadratic resistance law for rough channels with the maximum degree of turbulence in the tubular mixing device

At present, it is customary to consider the process of turbulence as a state of eddy flow of a viscous fluid, in which the main characteristics of the flow change their magnitude irregularly and randomly. Turbulence is a dissipative process that develops only in an open system, provided that energy is supplied from an external source supporting the dynamics of this process. Turbulent fluid flow exists in the state of thermodynamic equilibrium, in which the kinetic energy of local flow perturbations, which is transferred due to viscous stresses into the internal energy of the medium (its heating), is constantly compensated by energy coming from outside.

The main characteristics of the turbulent flow are irregular pulsations of magnitudes of local instantaneous velocities in the flow field resulting in a forced movement of local fluid volumes, accompanied by intensive equalization of the concentrations of chemical ingredients contained therein, dispersion of emulsion droplets, solid particles of suspensions, and fragmentation of gas bubbles.

There is a maximum turbulence of the fluid, accompanied by the most energetic mixing of its volume with a developed turbulent regime of flow movement in the region of the quadratic resistance law for rough channels.

In the region of developed turbulence, described by the quadratic resistance law for rough channels, also called the region of the self-similar fluid flow regime (since λQ= const), the magnitude of the pipe friction factor λQ depends only on the value of the relative roughness \( \bar{\Delta } \) and does not depend on the Reynolds number Re.

In this region, the magnitude of the pipe friction factor is usually determined by the Prandtl equation (Prandtl 1942):

$$ \lambda_{Q} = \frac{0.25}{{\left( {\lg 3.7\frac{d}{\Delta }} \right)^{2} }} . $$
(16)

Figure 1 shows the dependences of the pipe friction factor λ on the value of the Reynolds number Re for circular cross-section pipes with different magnitudes of relative roughness \( \bar{\Delta } = \frac{\Delta }{d} \), obtained experimentally by Konstantinov et al. (1987).

Fig. 1
figure 1

Murin’s graphs: 1 is a curve of hydraulically smooth pipes, constructed according to the Blasius equation; 2 is a region of quadratic law of hydraulic resistance; 3 is a transition region; 4 is a curve separating the transition region and the quadratic law region; and 5 is a laminar regime line

Full size image

Murin’s graphs are analogous to the charts obtained by Colebrook (1939).

There is a less intense turbulization of the fluid flow in the transition zone of the flow than in the region of the developed turbulence. The pipe friction factor λ is influenced by both the Reynolds number Re value and the relative roughness magnitude \( \bar{\Delta } \).

The magnitudes of the pipe friction factor λ in the transition zone are usually determined by the equation (Sterenlikht 1984; Konstantinov et al. 1987):

$$ \lambda = 0.11\left( {\frac{\Delta }{d} + \frac{68}{\text{Re}}} \right)^{0.25} . $$
(17)

A particular case of turbulent fluid flow in a transition sublayer is a flow in hydraulic smooth pipes, under which the condition is met:

$$ \frac{\Delta }{d}\langle \langle \frac{68}{\text{Re}} . $$
(18)

In this case, formula (16) becomes the Blasius equation (curve 1 in Fig. 1):

$$ \lambda = \frac{0.316}{{\text{Re}^{0.25} }}. $$
(19)

Since in transition of the turbulent regime of fluid flow to the quadratic resistance law region, the magnitude of the pipe friction factor λ at the transition point will depend on the value of the equivalent roughness of the flow channel Δ (m) and will not depend on the pipe diameter magnitude d (m), then a modified Reynolds number can be used, in which the magnitude of equivalent roughness is taken as the linear dimension Δ (m):

$$ \text{Re}_{{\Delta {\text{CT}}}} = \frac{{\upsilon_{\text{CT}} \Delta }}{\nu } $$
(20)

where υCT is the average velocity at the critical transition point of a turbulent fluid flow into the region of the quadratic resistance law (m/s) and ν is the kinematic coefficient of the fluid viscosity (m2/s).

By analogy with formula (9), which is valid in the case of a laminar regime of fluid movement, we assume that using this Reynolds number, the magnitude of the pipe friction factor λCT at the critical point of a turbulent fluid flow transition into the region of the quadratic resistance law can be determined by the following formula:

$$ \lambda_{\text{CT}} = \left( {\frac{64}{{\text{Re}_{{\Delta {\text{CT}}}} }}} \right)^{2} = \left( {\frac{64}{{\text{Re}_{\text{CT}} }} \cdot \frac{d}{\Delta }} \right)^{2} , $$
(21)

where

$$ \text{Re}_{\text{CT}} = \frac{64}{{\sqrt {\lambda_{\text{CT}} } }} \cdot \frac{d}{\Delta }. $$
(22)

In this case, taking into account formula (11), there will be an expression

$$ \lambda_{\text{CT}} = \left( {\frac{64}{{\text{Re}_{{\Delta {\text{CT}}}} }}} \right)^{2} = \left( {\frac{64}{{\text{Re}_{\text{CT}} }} \cdot \frac{d}{\Delta }} \right)^{2} = \frac{64}{{\text{Re}_{\text{CT}} }}\alpha_{\text{CT}} . $$
(23)

Curve 4 in Fig. 1, which characterizes the locations of the transition points of the turbulent regime of fluid movement in the region of the quadratic resistance law of rough channels (critical points of the turbulent regime), was constructed by formula (22).

The magnitude of the pipe friction factor in the developed turbulence regime (quadratic resistance law) is the constant (λ = λCT = const) and can be determined using the Prandtl Eq. (16). Substituting expression (16) into formula (22), we get

$$ \text{Re}_{\text{CT}} = \frac{64}{{\sqrt {0.25} }} \cdot \frac{d}{\Delta }\lg \left( {3.7\frac{d}{\Delta }} \right) = 128\frac{d}{\Delta }\lg \left( {3.7\frac{d}{\Delta }} \right). $$
(24)

A mathematical relation for critical points of the turbulent regime was proposed by Nikuradse (1932)

$$ \Delta = \frac{2N\nu }{{\upsilon_{{*{\text{CT}}}} }}\;({\text{m}}), $$
(25)

where υ*CT is the dynamic velocity magnitude at the critical point of the turbulent regime (m/s) and N is the Nikuradse number. According to experimental data, N = 10.9…11.5 (Konstantinov et al. 1987).

Taking into account the expression for dynamic velocity (3), formula (25) can be represented as:

$$ \upsilon_{{*{\text{CT}}}} = \frac{2N\nu }{\Delta } = \upsilon_{\text{CT}} \sqrt {\frac{{\lambda_{\text{CT}} }}{8}} \;({\text{m/s}}), $$
(26)

where

$$ \lambda_{\text{CT}} = 8\left( {\frac{2N\nu }{{\Delta \cdot \upsilon_{\text{CT}} }}} \right)^{2} = 32\left( {\frac{N}{{\text{Re}_{{\Delta {\text{CT}}}} }}} \right)^{2} , $$
(27)

Taking into account formulas (21) and (27), we get:

$$ \lambda_{\text{CT}} = \left( {\frac{64}{{\text{Re}_{{\Delta {\text{CT}}}} }}} \right)^{2} = 32\left( {\frac{N}{{\text{Re}_{{\Delta {\text{CT}}}} }}} \right)^{2} , $$
(28)

where \( N = 64 /\sqrt {32} = 11.314. \)

Nikuradse made the assumption that the thickness of the viscous sublayer δ*CT is two times less than the magnitude of equivalent roughness Δ (Fig. 2) at the considered critical points of the turbulent fluid flow, and the condition is met:

$$ \delta_{*} = \frac{1}{2}\Delta = \frac{N\nu }{{\upsilon_{{*{\text{CT}}}} }}\; \left( {\text{m}} \right). $$
(29)
Fig. 2
figure 2

Scheme for a viscous wall sublayer in hydraulically smooth pipes (a), and rough pipes at υ = υCT (m/s) and δ* = Δ/2 according to Nikuradse (b)

Full size image

The velocity gradient in the wall viscous sublayer can be determined by the following formula:

$$ G_{*} = \frac{{\upsilon_{*}^{2} }}{{\nu_{*} }} = \frac{{u_{*} }}{{\delta_{*} }}\; \left( {{\text{s}}^{ - 1} } \right), $$
(30)

where u* is the local velocity (m/s) at the boundary of the viscous sublayer at a distance from the wall y = δ* (m).

From formula (30), we have:

$$ \delta_{*} = \frac{{u_{*} }}{{\upsilon_{*} }}\frac{{\nu_{*} }}{{\upsilon_{*} }}\,({\text{m}}). $$
(31)

When analyzing formula (31), one of the following two assumptions can be made.

The first assumption is based on the ideas of Nikuradse, according to which the magnitude of the kinematic viscosity coefficient in the wall sublayer ν* is equal to the magnitude of the kinematic viscosity coefficient of the fluid ν in the flow kernel. The velocity at the boundary of the viscous sublayer at a distance of y = δ* from the pipe wall u* is not equal to the dynamic velocity magnitude (u* ≠ υ*). The ratio of the local velocity at the boundary of the wall sublayer u* to the dynamic velocity υ* is the Nikuradse number (N = u*/υ*), while the thickness of the wall sublayer δ* is equal to half of the equivalent roughness (δ* = Δ/2) and can be determined by formula (29).

The second assumption suggests that the magnitude of the velocity at the boundary of the viscous sublayer u* is equal to the magnitude of the dynamic velocity υ* (u* = υ*, u*/υ* = 1).

The magnitude of kinematic viscosity coefficient in the wall sublayer ν* is α times higher than the magnitude of the kinematic viscosity coefficient of a fluid in the flow kernel ν (ν* = αν). In this case,

$$ \delta_{*} = \frac{{u_{*} }}{{\upsilon_{*} }}\frac{\alpha \nu }{{\upsilon_{*} }} = \frac{\alpha \nu }{{\upsilon_{*} }}\;({\text{m}}). $$
(32)

Formula (32) is valid in any regime of fluid movement.

The magnitude of the coefficient αCT can be defined from formula (11) by substituting expression (22) as follows:

$$ \alpha_{\text{CT}} = \frac{{\lambda_{\text{CT}} \text{Re}_{\text{CT}} }}{64} = \frac{{\lambda_{\text{CT}} }}{64} \cdot \frac{64}{{\sqrt {\lambda_{\text{CT}} } }} \cdot \frac{d}{\Delta } = \frac{d}{\Delta }\sqrt {\lambda_{\text{CT}} } . $$
(33)

Taking into account the value of δ* from formula (7) and using formula (33), we have

$$ \alpha_{\text{CT}} = \frac{d}{\Delta }\sqrt {\lambda_{\text{CT}} } = \frac{4R}{\Delta }\sqrt {\lambda_{\text{CT}} } \frac{{\sqrt {32} }}{{\sqrt {32} }} = 4\sqrt {32} \frac{{\delta_{*} }}{\Delta }, $$
(34)

if δ* = Δ/2, \( \alpha_{\text{CT}} = 4\sqrt {32} /2 = 11.314. \)

Comparing the obtained values of the Nikuradse number N with the magnitude αCT, it can be concluded that the Nikuradse number N shows how many times the value of the kinematic viscosity coefficient ν* = αν increases at the critical point of the turbulent regime in a certain hypothetical viscous wall sublayer having a thickness of δ* = Δ/2.

It should be noted that in reality the thickness of the viscous sublayer δ*CT will be equal to the magnitude determined by formula (7), and the magnitude of the coefficient αCT will be equal to

$$ \alpha_{\text{CT}} = \frac{{\upsilon_{*} \delta_{*} }}{\nu } = \frac{{\upsilon_{\text{CT}} R}}{\nu }\frac{{\lambda_{\text{CT}} }}{16}. $$
(35)

Both the first and the second assumptions describe the real situation taking place in the wall layer of the turbulent flow, but observed in different periods of time.

The second assumption describes the moment of time when there are both a wall sublayer and a transition sublayer, and they together form a wall layer.

The first assumption describes the moment of time when the formation of turbulent eddies in the transition sublayer occurred, which leads to its destruction (decrease in the thickness of the wall layer) and an increase in the local velocity at the boundary of the wall sublayer.

In the transition sublayer of turbulent fluid flow, there is an abrupt decrease in the magnitude of the shear stress of longitudinal internal friction forces. It leads to the transformation of elastic potential energy, accumulated in the wall sublayer, into the energy of elementary turbulent eddies formatting in the transition sublayer, and an increase in the kinetic energy of fluid movement at the boundary of transition sublayer and flow kernel.

The process of the formation of turbulent eddies in the transition sublayer leads to its destruction, as a result of which there is a decrease in the thickness of the wall layer δ and an increase in the velocity at the boundary of the wall sublayer up to the value of ū* = Nυ*.

Fluctuations in the thickness of the wall layer δ, and the magnitude of the local velocity ūδ* at the boundary of the wall and transition sublayer, were detected during the study of the characteristics of turbulent flow near the pipe wall. It was found that the Nikuradse number is a pulsating quantity, changing its value in time from N = 2.3 to N = 18 (Sterenlikht 1984). The Nikuradse number averaged over a sufficiently long time interval has a constant value.

Calculation of hydrodynamic characteristics of the wall region of the fluid flow in a turbulent hydrodynamic mixing device

A great contribution to the development of ideas on the turbulent flow was made by Richardson (1920), who expressed the fruitful hypothesis of the diminution of atmospheric turbulence. He suggested that when large air masses move, the moving flow becomes unstable due to the roughness of the surface, which results in formation of large eddies, causing velocity pulsations stipulating atmospheric turbulence. The resulting eddies take their energy from the total energy of the entire moving air stream.

Nascent eddies have a linear scale L (m) (outer scale of turbulence), comparable to the scale of the whole stream. Large-scale turbulent eddies become unstable and break up into eddies of a smaller scale l (m), and they, in turn, break up into even smaller ones. This process of “grinding down” the scales of turbulent eddies continues farther away, while the energy of large eddies taken from the energy of a moving stream is transferred to smaller eddies, down to the smallest ones with an outer scale l0, where viscosity plays a significant role, and the energy of these eddies is transformed into heat.

The Richardson hypothesis was developed by Kolmogorov (1941) and Obukhov (1941) for liquids. In these works, the developed turbulence is considered as an isotropic process of changing the spatial scales of turbulent eddies l (m), occurring in the inertial interval, in which the dynamics of turbulent velocity pulsations depend only on the characteristic scale of perturbation and the magnitude of the energy dissipation εT [J/(kg s)].

In the inertial region of the pulsation scale (L ≥ l>l0), viscosity does not play a significant role; the energy simply flows from turbulent pulsations of a larger scale to smaller ones, and the value of the specific energy dissipation per unit mass of fluid per unit time εT [J/(kg s)] is a certain function of changing the velocity of turbulent disturbances Δυl (m/s) at a distance (scale) l (m):

$$ \varepsilon_{T} = f(\Delta \upsilon_{l} ,l)\;\left[ {{\text{J/}}({\text{kg}}\;{\text{s}});\;{\text{m}}^{2} / {\text{s}}^{3} } \right]. $$
(36)

Considering dimensions Δυl (m/s) and l (m), one can make only one combination that has the dimension [J/(kg s); m2/s3]

$$ \varepsilon_{T} = \frac{{\Delta \upsilon_{l}^{3} }}{l}\; \left( {{\text{m}}^{2} / {\text{s}}^{3} } \right). $$
(37)

Since the mass specific energy dissipation has a constant value (εT= const) in the considered inertial spectral interval of the eddies, starting with the outer scale L and ending with the inner scale l0, then for a given flow, you can write

$$ \Delta \upsilon_{l} = (\varepsilon_{T} l)^{1/3} \left( {\text{m/s}} \right). $$
(38)

The scale of turbulent pulsations l, having a turbulent composition of velocity pulsations Δυl, is related to the value of the local Reynolds number Rel by the ratio

$$ \text{Re}_{l} = \frac{{l\Delta \upsilon_{l} }}{\nu } $$
(39)

When reducing the scale of turbulent velocity pulsations to a certain value l0 (inner scale of turbulence), the value of local Reynolds criterion Rel becomes of order unity, and the viscosity of the flow will play the decisive role. In this case, the magnitude of the inner scale of turbulence can be defined from (39), taking (38) into account

$$ \text{Re}_{l} = \frac{{l_{0} \left( {\varepsilon_{T} l_{0} } \right)^{1/3} }}{\nu } = 1, $$
(39.1)

where

$$ l_{0} = \sqrt[4]{{\frac{{\nu^{3} }}{{\varepsilon_{T} }}}}\;\left( {\text{m}} \right). $$
(40)

From (38) and (40), we have

$$ \Delta \upsilon_{l0} = \left( {\varepsilon_{T} l_{0} } \right)^{1/3} = \left( {\varepsilon_{T} \frac{{\nu^{3/4} }}{{\varepsilon_{T}^{1/4} }}} \right)^{1/3} = \sqrt[4]{{\varepsilon_{T} \nu }}\;({\text{m/s}}). $$
(41)

Since the velocity gradient of turbulent pulsations of a zero scale Gl0 (s−1) is defined as the ratio of the velocity of turbulent pulsations of a zero scale Δυl0 (m/s) to the scale of turbulent pulsations l0 (m), then, taking into account (40) and (41), we obtain

$$ G_{l0} = \frac{{\Delta \upsilon_{l0} }}{{l_{0} }} = \sqrt[4]{{\varepsilon_{T} \nu }}\frac{1}{{\sqrt[4]{{\frac{{\nu^{3} }}{{\varepsilon_{T} }}}}}} = \sqrt {\frac{{\varepsilon_{T} }}{\nu }} \; \left( {{\text{s}}^{ - 1} } \right). $$
(42)

Thus, turbulent pulsations of the zero-scale (inner scale) flow rate will have the following characteristics:

  1. 1.

    Scale of turbulent pulsations (zero scale) l0 (m).

  2. 2.

    Zero-scale turbulent pulsation velocity Δυl0 (m/s).

  3. 3.

    Zero-scale turbulent pulsation velocity gradient Gl0 (s−1).

Their value can be described by the system of equations

$$ \begin{aligned} l_{0} & = \sqrt[4]{{\frac{{\nu^{3} }}{{\varepsilon_{T} }}}}\; \left( {\text{m}} \right) \\ \Delta \upsilon_{l0} & = \sqrt[4]{{\varepsilon_{T} \nu }}\;({\text{m/s}}) \\ G_{l0} & = \sqrt {\frac{{\varepsilon_{T} }}{\nu }} \;({\text{s}}^{ - 1} ) \\ \end{aligned} $$
(43)

The value of the specific second energy dissipation can be defined as the ratio of the energy loss during steady-state uniform flow of fluid A (J), over the length of the flow section L (m), to the product of this flow mass m (kg) by the duration of the dissipation process T (s)

$$ \varepsilon_{T} = \frac{A}{mT},\;\left[ {{\text{J/}}({\text{kg s}});\;{\text{m}}^{2} / {\text{s}}^{3} } \right]. $$
(44)

Since A = LωΔP = LωρgiL; m = Lωρ; T = L/υ, where ΔP = ρgiL is the pressure loss (Pa) at the flow length L (m) and ω is the area of the flow cross section (m2), then

$$ \varepsilon_{T} = \frac{L\omega \rho giL}{L\omega \rho }\frac{\upsilon }{L} = gi\upsilon \; \left( {{\text{m}}^{2} / {\text{s}}^{3} } \right). $$
(45)

Considering \( i = \frac{\lambda }{d}\frac{{\upsilon^{2} }}{2g} \); \( \upsilon_{*}^{2} = igR \); and \( G_{ * } = \frac{2\upsilon }{R} \), formula (45) can be represented as

$$ \varepsilon_{T} = gi\upsilon \frac{\rho L}{\rho L} = \frac{\Delta P}{\rho }\frac{\upsilon }{L}\; \left( {{\text{m}}^{2} / {\text{s}}^{3} } \right), $$
(46)
$$ \varepsilon_{T} = gi\upsilon = g\upsilon \frac{\lambda }{d}\frac{{\upsilon^{2} }}{2g} = \frac{1}{2}\frac{\lambda }{d}\upsilon^{3} \; \left( {{\text{m}}^{2} / {\text{s}}^{3} } \right), $$
(47)
$$ \varepsilon_{T} = gi\upsilon \frac{R}{R} = \upsilon_{*}^{2} \frac{\upsilon }{R} = \frac{1}{2}\upsilon_{*}^{2} G_{*} \; \left( {{\text{m}}^{2} / {\text{s}}^{3} } \right). $$
(48)

Considering \( \varepsilon_{T} = \frac{1}{2}\upsilon_{*}^{2} G_{*} \); \( G_{*} = \frac{{\upsilon_{*}^{2} }}{\alpha \nu } \); and \( \frac{{\upsilon_{*} }}{{G_{*} }} = \delta_{*} \), the system of Eq. (43) can be transformed as follows:

$$ l_{0} = \sqrt[4]{{\frac{{\nu^{3} }}{{\varepsilon_{T} }}}} = \sqrt[4]{{\frac{{\nu^{3} }}{{\frac{1}{2}\upsilon_{*}^{2} G_{*} }}}} = \sqrt[4]{{\frac{{2\nu^{3} }}{{\upsilon_{*}^{2} \frac{{\upsilon_{*}^{2} }}{\alpha \nu }}}}} = \frac{\nu }{{\upsilon_{*} }}\frac{{\upsilon_{*} }}{{\upsilon_{*} }}\frac{\alpha }{\alpha }\sqrt[4]{2\alpha } = \frac{{\upsilon_{*} }}{{G_{*} }}\sqrt[4]{{\frac{2}{{\alpha^{3} }}}} = \delta_{*} \sqrt[4]{{\frac{2}{{\alpha^{3} }}}}\;({\text{m}}) $$
(49)
$$ \Delta \upsilon_{l0} = \sqrt[4]{{\varepsilon_{T} \nu }} = \sqrt[4]{{\frac{1}{2}\upsilon_{*}^{2} G_{*} \nu }} = \sqrt[4]{{\frac{1}{2}\upsilon_{*}^{2} \frac{{\upsilon_{*}^{2} }}{\alpha \nu }\nu }} = \upsilon_{*} \sqrt[4]{{\frac{1}{2\alpha }}}\;({\text{m/s)}} $$
(50)
$$ G_{l0} = \sqrt {\frac{{\varepsilon_{T} }}{\nu }} = \sqrt {\frac{1}{2}\upsilon_{*}^{2} G_{*} \frac{1}{\nu }\frac{\alpha }{\alpha }} = G_{*} \sqrt {\frac{\alpha }{2}} \;({\text{s}}^{ - 1} ) $$
(51)

Thus, we have a system of equations describing turbulent pulsations of zero-scale velocity:

$$ \begin{aligned} l_{0} & = \delta_{*} \sqrt[4]{{\frac{2}{{\alpha^{3} }}}}\;({\text{m}}) \\ \Delta \upsilon_{l0} & = \upsilon_{*} \sqrt[4]{{\frac{1}{2\alpha }}}\;({\text{m/s}}) \\ G_{l0} & = G_{*} \sqrt {\frac{\alpha }{2}} \;({\text{s}}^{ - 1} ) \\ \end{aligned} $$
(52)

Along with vortex turbulence developing in the volume of a liquid, there is also wave turbulence observed on the surface of the liquid. The processes of energy dissipation for the wave turbulence are studied more fully than for the vortex one. The wave arising on the surface of a liquid has a smooth surface, the wavelength L (m) and a certain oscillation frequency νL, which determines the level of its energy.

After some time, ripples appear on the wave surface of the wave, that is, oscillations having a higher frequency νl (and, therefore, energy) and a smaller wavelength l (Fig. 3). These oscillations are usually called low-scale turbulence. The processes of energy transfer from the current wave (large-scale turbulence) to low-scale turbulence are called a direct cascade of energy.

Fig. 3
figure 3

Scheme of wave motion while reducing wave energy during the process of ripple formation on its surface

Full size image

During the direct cascade, the oscillation frequency and, consequently, the energy of low-scale turbulence increase, and the ripple wavelength l (low-scale turbulence) decreases. When a certain critical value of the wavelength l0 is reached, the inertia forces causing it are equal in magnitude to the friction forces. As a result, the energy contained in it will dissipate into the environment and turn into heat.

As a result of the reverse energy cascade, the frequency of the carrier wave and its energy decrease, and the scale (wavelength L) increases.

We assumed that the mechanism of energy dissipation for vortex turbulence is based on the same principles as for wave turbulence (Andreyev 2005).

Elementary turbulent eddies with a scale lδ, arising in the transition sublayer, have a certain moment of rotational motion Ml= lδυ*Δm, which was not observed in the flow before their appearance. According to the law of conservation of angular momentum, the elementary eddies formed should move around a certain center in the direction opposite to the direction of their rotation, resulting in a turbulent mole having a scale L (m), orbital velocity uL (m/s), and angular momentum ML= LuLΔm (Fig. 4). The formation of a turbulent mole makes it possible to compensate the arising rotational motion momentum Ml= lδυ*Δm, while

$$ \begin{aligned} M_{l} & = {-}M_{L} \\ l_{\delta } \upsilon_{*} \Delta m & = {-}Lu_{L} \Delta m \\ l_{\delta } \upsilon_{*} & = {-}Lu_{L} \\ \end{aligned} $$
(53)
Fig. 4
figure 4

Scheme for the formation of a turbulent mole (planetary mechanism of vortex turbulence)

Full size image

The orbital diameter of turbulent eddy rotation will determine the size of large-scale turbulence (turbulent mole) L.

The magnitude of a single turbulent eddy will determine the size of low-scale turbulence lδ.

In accordance with the planetary hypothesis of the mechanism of vortex turbulence, the resulting turbulent moles will interact with the carrying fluid flow and experience the Magnus effect, leading to a drift of turbulent moles to the flow axis.

Under the influence of a direct energy cascade, the size of an elementary turbulent vortex l (low-scale turbulence) will decrease, and the amount of energy enclosed therein will increase. When reducing the size of the elementary turbulent vortex to a critical value l0, there will be a dissipation of contained energy into the environment.

Reverse energy cascade provides an increase in the diameter of the turbulent mole orbital L (size of large-scale turbulence) and reduction in the frequency of planetary rotation and, consequently, the energy of the large-scale turbulence.

Turbulent eddies originating in the transition sublayer cause the appearance of the low-scale velocity pulsation component in the wall regions of the flow. They have the value of the coefficient of kinematic viscosity ν* = αν. Their characteristics can be described by a system of equations

$$ \begin{aligned} l_{\delta } & = \sqrt[4]{{\frac{{\nu_{*}^{3} }}{{\varepsilon_{T} }}}} = \sqrt[4]{{\frac{{\alpha^{3} \nu^{3} }}{{\varepsilon_{T} }}}}\;({\text{m}}) \\ \Delta \upsilon_{l} & = \sqrt[4]{{\varepsilon_{T} \nu_{*} }} = \sqrt[4]{{\varepsilon_{T} \alpha \nu }}\;({\text{m/s}}) \\ G_{l} & = \sqrt {\frac{{\varepsilon_{T} }}{{\nu_{*} }}} = \sqrt {\frac{{\varepsilon_{T} }}{\alpha \nu }} \;({\text{s}}^{ - 1} ) \\ \end{aligned} $$
(54)

taking into account \( \varepsilon_{T} = \frac{1}{2}\upsilon_{*}^{2} G_{*} \); \( G_{*} = \frac{{\upsilon_{*}^{2} }}{\alpha \nu } \); and \( \frac{{\upsilon_{*} }}{{G_{*} }} = \delta_{*} \).

The system of Eq. (54) can be transformed as follows:

$$ l_{\delta } = \sqrt[4]{{\frac{{\nu_{*}^{3} }}{{\varepsilon_{T} }}}} = \sqrt[4]{{\frac{{\alpha^{3} \nu^{3} }}{{\frac{1}{2}\upsilon_{*}^{2} G_{*} }}}} = \sqrt[4]{{\frac{{2\alpha^{3} \nu^{3} }}{{\upsilon_{*}^{2} \frac{{\upsilon_{*}^{2} }}{\alpha \nu }}}}} = \frac{\alpha \nu }{{\upsilon_{*} }}\frac{{\upsilon_{*} }}{{\upsilon_{*} }}\frac{\alpha }{\alpha }\sqrt[4]{2} = \frac{{\upsilon_{*} }}{{G_{*} }}\sqrt[4]{2} = \delta_{*} \sqrt[4]{2}\;({\text{m}}) $$
(55)
$$ \Delta \upsilon_{l} = \sqrt[4]{{\varepsilon_{T} \nu_{*} }} = \sqrt[4]{{\frac{1}{2}\upsilon_{*}^{2} G_{*} \alpha \nu }} = \sqrt[4]{{\frac{1}{2}\upsilon_{*}^{2} \frac{{\upsilon_{*}^{2} }}{\alpha \nu }\alpha \nu }} = \upsilon_{*} \sqrt[4]{{\frac{1}{2}}}\;({\text{m/s}}) $$
(56)
$$ G_{l} = \sqrt {\frac{{\varepsilon_{T} }}{{\nu_{*} }}} = \sqrt {\frac{1}{2}\upsilon_{*}^{2} G_{*} \frac{1}{\alpha \nu }} = G_{*} \sqrt {\frac{1}{2}} \;({\text{s}}^{ - 1} ) $$
(57)

Thus, we obtain the system of equations:

$$ \begin{aligned} l_{\delta } & = \delta_{*} \sqrt[4]{2}\;({\text{m}}) \\ \Delta \upsilon_{l} & = \upsilon_{*} \sqrt[4]{{\frac{1}{2}}}\;({\text{m/s}}) \\ G_{l} & = G_{*} \sqrt {\frac{1}{2}} \;({\text{s}}^{ - 1} ) \\ \end{aligned} $$
(58)

The existing empirical evidence suggests that the most intense mixing in turbulent flows occurs in the wall region (Adelshin and Potekhin 1997). The efficiency of mixing the liquid is characterized by the turbulent diffusion coefficient DT (m2/s).

Turbulent velocity pulsations ΔυL, having a scale of l ≤ L, are responsible for the relative displacement of two liquid microvolumes at a distance L (m) from each other during mixing in a turbulent flow, since both liquid microvolumes will move as a whole at l ≥ L. In this regard, the magnitude of the turbulent diffusion coefficient in the wall region of the tubular mixer can be defined as:

$$ D_{{{\text{T}}l}} = 2l_{\delta } \Delta \upsilon_{l} \;({\text{m}}^{2} / {\text{s}}). $$
(59)

Taking (55) and (56) into account, we can write:

$$ D_{{{\text{T}}l}} = 2l_{\delta } \Delta \upsilon_{l} = 2\sqrt[4]{{\frac{{\alpha^{3} \nu^{3} }}{{\varepsilon_{T} }}}}\sqrt[4]{{\varepsilon_{T} \alpha \nu }} = 2\alpha \nu \; ({\text{m}}^{2} / {\text{s}}). $$
(60)

In the axial flow region in the spectrum of turbulent velocity pulsations, zero-scale turbulent pulsations will prevail. In this case:

$$ D_{{{\text{T}}l0}} = 2l_{0} \upsilon_{l0} = 2\sqrt[4]{{\frac{{\nu^{3} }}{{\varepsilon_{T} }}}}\sqrt[4]{{\varepsilon_{T} \nu }} = 2\nu \; ({\text{m}}^{2} / {\text{s}}). $$
(61)

Investigations of turbulent flows in a circular cross-section tubes have allowed us to obtain an empirical formula for determining the magnitude of the pulsations of the flow velocity component in the wall region (Levich 1958):

$$ \Delta \upsilon_{l}^{a} = \frac{0.2\upsilon }{{\text{Re}^{0.125} }}\; \left( {\text{m/s}} \right). $$
(62)

In the work Adelshin and Potekhin (1997), formula was given that allows to determine the coefficient of turbulent diffusion in the wall region of the fluid flow moving in a circular cross-section pipe:

$$ D_{\text{T}}^{a} = \frac{0.0033d\upsilon }{{\text{Re}^{0.125} }}\;\left( {{\text{m}}^{2} / {\text{s}}} \right). $$
(63)

Results and discussion

Theoretical studies of hydrodynamic regularities of fluid flow in pressure channels of circular cross section made it possible to conclude that the maximum turbulence of fluid flow, accompanied by the most vigorous mixing of its volume, is observed with a developed turbulent flow motion in the region of the quadratic resistance law for rough channels. The transition of the fluid flow regime to the region of the quadratic resistance law for rough channels is observed at the critical points of the turbulent flow, characterized by the critical Reynolds number ReCT. The value of the critical Reynolds number ReCT at critical points of turbulent flow is proportional to the value of the coefficient of hydraulic friction λCT at these points to − 0.5 power and the relative roughness of the flow channels \( \overline{\Delta } = \frac{\Delta }{d} \) to − 1 power. At the critical point of the turbulent flow, the Nikuradse number, representing the ratio of the magnitude of the local velocity u* on the border of a hypothetical wall sublayer having a thickness δ*, equal to half the equivalent roughness Δ, to the magnitude of the dynamic velocity υ*, is N = 11.314. The thickness of the viscous wall sublayer has a value determined by formula (7) at the critical point of the turbulent flow. The value of the coefficient of kinematic viscosity (ν* = αν) in the viscous wall sublayer of the turbulent flow increases α times, so does the value of the coefficient of hydraulic friction λ.

The main hydrodynamic characteristics of the wall region of a turbulent fluid flow are the pulsating component of the flow velocity Δυl (m/s) and turbulent diffusion coefficient DT (m2/s). In these areas, elementary turbulent eddies are generated, causing the appearance of a low-scale component of the turbulent flow velocity pulsations. Elementary turbulent eddies form turbulent moles by a planetary mechanism, causing the appearance of a large-scale component of the turbulent pulsation of the flow velocity. Turbulent moles interact with the carrying fluid flows and drift toward their axis. Under the influence of the direct energy cascade, the linear dimensions of elementary turbulent eddies decrease and reach a critical value l0 (internal scale of turbulence), resulting in dissipation of the energy contained therein.

The magnitude of the turbulent diffusion coefficient in the wall flow region DTl is α times higher than the value of the turbulent diffusion coefficient in the axial flow region:

$$ D_{{{\text{T}}l}} = \alpha D_{{{\text{T}}l0}} \; ({\text{m}}^{2} / {\text{s}}). $$
(64)

The magnitudes of low-scale turbulent pulsations of the flow velocity in the wall region exceed the magnitude of turbulent pulsations of zero-scale velocity in the near-axial flow region \( \sqrt[4]{\alpha } \) times

$$ \Delta \upsilon_{l} = \sqrt[4]{\alpha }\Delta \upsilon_{l0} \; \left( {\text{m/s}} \right). $$
(65)

Table 1 presents the values of the velocity gradient G* in the wall sublayer, calculated by formula (6), the specific second energy dissipation εT, calculated by formula (48), coefficient α, calculated by the formula

$$ \alpha = \frac{{\lambda \text{Re} }}{64}, $$
(66)
Table 1 The calculation results
Full size table

the pulsating component of the flow rate \( \Delta \upsilon_{l}^{a} \), calculated by formula (62), and \( \Delta \upsilon_{l} \), calculated by the formula (53), as well as the values of the turbulent diffusion coefficients in the wall flow region \( D_{\text{T}}^{a} \), calculated by formula (63), and DTl, calculated by formula (60) in a tubular hydrodynamic mixing device with a diameter of d = 0.05 m with an equivalent roughness of Δ = 0.1 × 10−3 m.

The values of hydraulic friction factor λ were determined by the Altshul Eq. (17) in the transition zone and by the Prandtl Eq. (16) in the quadratic resistance law for rough channels.

The values of the Reynolds number at the critical point of transition of the turbulent regime in the region of the quadratic resistance law were determined by formula (22).

In accordance with the data given in Adelshin and Potekhin (1997), formulas (62) and (63) were obtained in the range of Reynolds numbers Re = 100,000–150,000.

Data given in Table 1 show that the relative error of the values of the pulsation velocities, calculated by the empirical formula (62) and the theoretical formula (56) proposed by us in the velocity range υ = 2–3 m/s, does not exceed 3.0%, and the relative error of the values of the turbulent diffusion coefficients, calculated by the empirical formula (63) and the theoretical formula (60), however, does not exceed 2.7%.

Conclusions

A new method for calculating hydrodynamic characteristics of a turbulent fluid flow in pressure channels of circular cross section is proposed. The main mathematical relations, which allow determining the values of the main parameters of the turbulent fluid flow in the pressure channel of circular cross section, are obtained. The resulting mathematical relationships are shown in Table 2.

Table 2 The resulting mathematical relationships
Full size table

Using the proposed method for calculating the hydrodynamic characteristics of a turbulent fluid flow in pressure channels, it is possible to optimize the operation mode of tubular mixing devices in terms of technological efficiency and energy consumption in the process of reagent wastewater treatment.