Spreading speeds of invasive species in a periodic patchy environment: effects of dispersal based on local information and gradient-based taxis

Abstract

We consider a periodic environment with favorable and unfavorable patches alternately arranged in one dimension. In such heterogeneous environments, invasive animals may undergo not only random diffusion but also directed movement toward favorable patches. Here we propose reaction–diffusion–advection models in which the diffusion term is of either Fickian or Fokker–Planck type, the advection term is given by a gradient-based taxis, and the growth rate depends on both the environmental conditions and the population density. We first present hypotheses for the existence of a periodic traveling wave and a method to derive its spreading speed. Then this method is applied to a case in which the environment is homogeneous within each patch, so that taxis occurs at interfaces between different patches, causing accumulated distributions in favorable patches with density jumps at the interfaces. We show how the Fickian or Fokker–Planck diffusion and the gradient-based taxis interplay to determine the spreading speed.

1 Introduction

Environments in nature are generally heterogeneous as the consequence of natural processes or human activities causing habitat fragmentation. In such heterogeneous environments, the dispersal of organisms could be influenced by various factors such as spatially varying diffusion and directed movement toward more favorable habitat (taxis). At the same time, the rate of population growth would also change depending on the favorability of environments. In this article, we introduce reaction–diffusion–advection equations incorporating the above spatially dependent dispersal and growth processes, and investigate how these factors interplay in determining the spatio-temporal distribution of invasive species and its rate of spread. As for the spatial heterogeneity, we consider a simple periodically varying environment, in which a favorable patch and an unfavorable patch are alternately arranged in one dimension [36].

Many organisms from bacteria to mammals have abilities to migrate in response to stimuli or signals indicating foods, favorable or unfavorable habitats, prey or predators, etc., through various senses such as sight, hearing, smell, touch and so on. Since the pioneering work by Keller and Segel [17, 18] on bacterial chemotaxis, various mathematical models in the framework of reaction–diffusion–advection equations have been proposed and used to investigate the taxis-induced pattern formations widely observed in not only microorganisms but also higher animals [1, 2, 6, 8, 9, 13, 14, 23, 28, 29, 31, 34, 38, 41]. However, there have been relatively few works on the effect of taxis on the range expansion pattern of invading species and its spreading speed in heterogeneous environments, but see Kawasaki et al. [15], Maciel and Lutscher [24] and Berestycki et al. [3].

In the present work, we employ two types of reaction–diffusion–advection equations in one dimension in which diffusion terms are of the Fickian and Fokker–Planck types, and advection term is given by a gradient-based taxis:

Fickian reaction–diffusion–advection equation (Fickian RDA)

$$\begin{aligned} \frac{\partial n}{\partial t} = \frac{\partial }{\partial x}\left( D(x)\frac{\partial n}{\partial x} \right) - \frac{\partial u(x)n}{\partial x} + R(x, n)n \end{aligned}$$

(1)

Fokker–Planck reaction–diffusion–advection equation (Fokker–Planck RDA)

$$\begin{aligned} \frac{\partial n}{\partial t} = \frac{\partial ^2 D(x) n}{\partial x^2} - \frac{\partial u(x)n}{\partial x} + R(x, n)n \end{aligned}$$

(2)

where n(x, t) is the population density, D(x) is the diffusion coefficient, u(x) is the advection velocity which is assumed to be proportional to the gradient of the favorability of environment f(x), i.e., $u(x) \propto df(x)/dx$, and R(x, n) is the per capita growth rate. We also assume that D(x), u(x) and R(x, n) are periodic with period L in x.

1.1 Fickian diffusion vs Fokker–Planck diffusion and gradient-based taxis

The difference in movement behaviors between the two types of diffusions was previously discussed in the framework of a one-dimensional random walk model by Skellam [40] (see also Okubo and Levin [28], [12, 21, 41]).

If the transition probabilities $P_{i,i+1}$ and $P_{i+1,i}$ (the probabilities of moving from point i to point $i+1$ and from $i+1$ to i, respectively) depend only on the environmental conditions at the point of departure (i.e., local information), the diffusion term is given by $\partial ^2 D(x)n/\partial x^2$, which is designated here as Fokker–Planck diffusion after the terminology originally used by Turchin [41]. On the other hand, if both transition probabilities depend on the average condition between the two points (or the condition at the mid point) so that they are equal, the diffusion term is given by $\partial \{ D(x)\partial n/\partial x\}/\partial x$, which is designated as Fickian diffusion because this obeys the Fickian law. Since the Fokker–Planck diffusion term is rewritten as $\dfrac{\partial }{\partial x}\left( D(x)\dfrac{\partial n}{\partial x}\right) + \dfrac{\partial }{\partial x}\{ D'(x)n\}$, it can be regarded as the Fickian diffusion with an additional effective advection in the direction of decreasing D(x). Okubo and Levin [28] pointed out that the Fokker–Planck diffusion may be well suited to handle certain kinds of animal taxis (e.g., kinesis) and dispersal, while the Fickian type should be appropriate for the diffusion of physical properties and, in some cases, for biological diffusion in which the flux is always directed from high concentration to low concentration.

In the same framework of a one-dimensional random walk model as above, we derive the advection term induced by gradient-based taxis (Othmer and Steven [29]). Let us denote by f(i) the favorability at point i. The organism undergoes not only random diffusion (either Fickian or Fokker–Planck) but also directed movement at a rate proportional to the difference $f(i+1)-f(i)$ in the direction where $f(i+1)-f(i)$ is positive. Thus, the transition rates are assumed to be given,

$$\begin{aligned}&P_{i,i+1} = k_{i,i+1} + \beta \{f(i+1)-f(i)\},\\&P_{i+1,i} = k_{i+1,i} - \beta \{f(i+1)-f(i)\}, \end{aligned}$$

where $k_{i,i+1}$ and $k_{i+1,i}$ are the transition rates due to random walk and the second terms represent the transition rates due to the directed movement. If $k_{i,i+1}=k_{i+1,i}=k$, we have a diffusion advection equation

$$\begin{aligned} \dfrac{\partial n}{\partial t} = D\dfrac{\partial ^2 n}{\partial x^2} - \dfrac{\partial u(x)n}{\partial x}, \end{aligned}$$

where $D\,{=}\,\lim _{{\uplambda },\tau \rightarrow 0}({\uplambda }^2/\tau )k$ and $u(x)\,{=}\,\lim _{{\uplambda },\tau \rightarrow 0}({\uplambda }/\tau )\beta \{f(i+1)-f(i)\}$. ${\uplambda }$ is the distance between adjacent two points and $\tau$ is time interval of each step. When $k_{i,i+1}$ and $k_{i+1,i}$ satisfy the condition that yields Fickian or Fokker–Planck diffusion, we have the Fickian or Fokker–Planck diffusion–advection equation, respectively.

1.2 Layout of the paper

In Sect.  2, it is shown that the Eqs. (1) and (2) can be transformed into an equation for which under some assumptions the existence of asymptotic spreading speeds, the existence of periodic traveling waves, and the existence of certain periodic traveling waves of the linearization of the differential equations and the relations between their speeds and the asymptotic spreading speeds are known. This means that accurate approximations to the spreading speeds can be found from tractable computations. The present work is devoted to carrying out such computations in order to obtain insight into the variation of the speed with the parameters of the problem. In Sect. 3, we apply the mathematical method obtained in Sect. 2 to the Fickian RDA equation with a logistic growth rate for periodic patchy environments, where D(x) and $r(x) :=R(x,0)$ are both piecewise constant and u(x) is proportional to the gradient of r(x), and derive the asymptotic spreading speed of the periodic traveling wave. Numerical simulations are also carried out to examine effects of the gradient based taxis on the spatio-temporal patterns of the periodic traveling wave. In Sect. 4, a similar analysis is done for the Fokker–Planck RDA equation. Comparing the results from the Fickian and Fokker–Planck RDA equations, we discuss how the difference in the type of diffusion affects the pattern and the speed of the periodic traveling wave.

2 A model and its spreading speeds

We have presented two models (1) and (2) for the diffusion and advection of organisms. We shall make the following assumptions about the coefficients of these models.

Hypotheses 2.1

The prescribed functions in (1) and (2) have the following properties:

• i. The function D(x) is positive, L-periodic, continuous and piecewise differentiable, and its derivative $D'(x)$ is uniformly bounded and piecewise continuous.

• ii. The function u(x) is L-periodic, integrable, uniformly bounded and piecewise continuous.

• iii. There is a positive constant $\bar{n}$ such that

  $$\begin{aligned} R(x,n) \le 0\quad \text { for }\, n \ge \bar{n}. \end{aligned}$$

• iv. R(x, n) is L-periodic in x, and $r(x):=R(x,0)$ uniformly bounded.

• v. There is a constant $m>0$ such that if $0\le \mu \le \nu$, then for every x

  $$\begin{aligned} -m[\nu -\mu ] \le R(x,\nu )-R(x,\mu ) \le 0. \end{aligned}$$

• vi. There are an L-periodic uniformly bounded and uniformly positive function $\ell (x)$ and a positive constant $\gamma$ such that

  $$\begin{aligned}{}[D\ell '-u\ell ]'+R(x,0)\ell \ge \gamma \ell \quad \text { for equation (1)} \end{aligned}$$

  or

  $$\begin{aligned} \{[D\ell ]'-u\ell \}'+R(x,0)\ell \ge \gamma \ell \quad \text { for equation (2)}. \end{aligned}$$

Remark

In the numerical examples of this work, we shall set $u(x)=\alpha r'(x)$, where $r(x):=R(x,0)$. In this case, the Hypotheses 2.1.ii becomes the requirement that r(x) should be L-periodic, continuous and piecewise differentiable, with its derivative $r'(x)$ uniformly bounded and piecewise continuous.

In order to study (1) and (2) in a unified manner, we shall show how to reduce them to a simpler one by means of a trick.

Lemma 2.1

Let n(x, t) be a solution of the Eq. (1). The function

$$\begin{aligned} b(x)&=e^{\int _0^x\frac{u(y)}{D(y)}dy} \int _x^L \frac{e^{-\int _0^z\frac{u(y)}{D(y)}dy}}{D(z)}dz + \ e^{-\int _x^L \frac{u(y)}{D(y)}dy} \int _0^x \frac{e^{-\int _0^z \frac{u(y)}{D(y)}dy}}{D(z)}dz . \end{aligned}$$

(3)

is a uniformly positive uniformly bounded L-periodic solution of the equation

$$\begin{aligned}{}[D(x) b']'-[u(x)b]'=0. \end{aligned}$$

(4)

Therefore the new independent variable

$$\begin{aligned} v(x,t)=n(x,t)/b(x) \end{aligned}$$

(5)

satisfies the equation

$$\begin{aligned} v_t-D(x)v_{xx}-A(x)v_x- S(x,v)v=0, \end{aligned}$$

(6)

where

$$\begin{aligned}&A(x)=D'(x)-u(x)+2{D(x)b'(x)/b(x)} \nonumber \\&S(x,v)=R(x,b(x)v). \end{aligned}$$

(7)

Because Eq. (2) can be written as

$$\begin{aligned} n_t-[Dn_x]_x+\{[u-D']n\}_x-R(x,n)n=0 \end{aligned}$$

which is of the form (1), a solution of (2) can also be put into the form (6) by replacing u(x) by $u(x)-D'(x)$ in the definition (3) of b(x) and making the change of variable (5). Of course, u(x) must also be replaced by $u(x)-D'(x)$ in (7).

This lemma will be proved in the Appendix 1.

In order to study the large-time behavior of a solution of the reaction–diffusion–advection Eq. (6) we shall apply some results of Weinberger [43]. We must, of course, make some assumptions on the prescribed functions.

We now introduce a discrete-time evolution model which is naturally related to the continuous-time model (6). For any function $v_0(x)$ let v(x, t) be the solution of (6) with the initial values $v(x,0)=v_0(x)$, and define the time-1 operator Q by the condition that

$$\begin{aligned} Q[v_0](x):=v(x,1). \end{aligned}$$

Because the Eq. (6) has no explicit t-dependence, it is also true that for any $t\ge 0$ $v(x,t+1)=Q[v(\cdot ,t)](x)$. In particular, it is true that $Q[v(\cdot ,n)](x)=v(x,n+1)$. Thus we see that if we restrict the values of t to integers, any solution v(x, t) of (6) is mapped into the sequence of function $v_n(x):=v(x,n)$, and this sequence satisfies the recursion formula

$$\begin{aligned} v_{n+1}=Q[v_n]. \end{aligned}$$

(8)

Conversely, if we are given a solution of this recursion, we can recover a continuous-time solution of (6) by letting $v(x,n+t)$ be the solution of (6) with the initial value $v_n(x)$ and with $0\le t\le 1$. Because t is uniformly bounded in this process, it turns out that the large-time asymptotics of a solution of (6) are the same as the large-n asymptotics of a solution of the recursion (8).

Our results will be based on the following Lemma, which permits us transfer the results proved in Weinberger [43] to solutions of the Eq. (6).

Lemma 2.2

Let Hypotheses 2.1 be satisfied. Then the recursion (8) where Q is the time-one map Q of the Eq. (6) satisfies the conditions of all the Theorems and of Corollary 2.1 of Weinberger [43].

This lemma will be proved in the Appendix 2. Theorem 2.6 of Weinberger [43] concerns the speeds of periodic traveling waves (PTW) of the recursion (8). (Note that the periodic traveling wave has also been termed as “traveling periodic wave” [39] and “pulsating traveling front” [5].) A rightward PTW of speed c of the continuous-time Eq. (6) was defined by Shigesada et al. [39] and Berestycki et al. [5] to be a solution of (6) in the form

$$\begin{aligned} v(x,t)=W(x-ct,x) \end{aligned}$$

in which the function W(y, x) has the properties

• 1. For each y, the function W(y, x) is L-periodic in x.

• 2. For each x, the function W(y, x) is nonincreasing in y, and

  • a. ${\lim _{y\rightarrow +\infty }W(y,x)=0}$, and

  • b. ${\lim _{y\rightarrow -\infty }[\pi _1(x)-W(y,x)]=0,}$ where $\pi _1(x)$ is a uniformly positive L-periodic equilibrium solution of (6).

A leftward PTW of (6) of speed c is a solution of the form $v(x,t)=W(-x-ct,x)$ where W satisfies the same conditions.

Weinberger [43] gave a natural extension to define a rightward or leftward PTW of a recursion (8) to be a solution of (8) of the form $v_n(x):=W(\pm x-nc,x)$, where W(y, x) has the properties listed above. When Q is the time-one map of a continuous process, it is easily seen that a PTW of the recursion is simply the sequence obtained by setting $t=n$ in a PTW of the continuous process.

Once Lemma 2.2 has been proved, Theorems 2.1, 2.3, and 2.6 and Corollary 2.1 of [43] yield the following results.

Theorem 2.1

Let the Hypotheses 2.1 be satisfied. Then

• 1. There exists a uniformly positive L-periodic equilibrium solution $\pi _1(x)$ of (6). There also exist two numbers with $-c^*_-<c^*_+$ such that every solution v(x, t) of (6) with $0\le v(x,0)<\pi _1(x)$, $v(x,0)>0$ on an open interval, and $v(x,0)=0$ outside a bounded set has the properties

  $$\begin{aligned}&\lim _{t\rightarrow \infty } \max _{x\le -ct} v(x,t)=0\quad \mathrm{when}-c<-c^*_- \\&\lim _{t\rightarrow \infty }\max _{-c_- t\le x\le c_+ t}[\pi _1(x)-v(x,t)]=0\quad \mathrm{when}\ -c^*_-<-c_-<c_+<c^*_+ \\&\lim _{t\rightarrow \infty } \max _{x\ge ct} v(x,t)=0\quad \mathrm{when }\ c>c^*_+. \end{aligned}$$

  That is, $c^*_+$ is the rightward asymptotic spreading speed of any of a large family of initial value problems for (6) and $c^*_-$ is the leftward asymptotic spreading speed.

• 2. The rightward spreading speed $c^*_+$ can be characterized as the smallest c for which a rightward PTW of speed c exists. Also $c^*_-$ is the smallest speed of a leftward PTW of (6).

• 3. $c^*_+$ can also be characterized as the smallest speed c for which the linearization

  $$\begin{aligned} w_{t}-D(x)w_{xx}-A(x) w_{x}-S(x,0)w=0 \end{aligned}$$

  (9)

  of (6) has a solution of the form

  $$\begin{aligned} w(x,t)=e^{-{s}[x-ct]}\psi (x) \end{aligned}$$

  with ${s}>0$ and $\psi (x)$ L-periodic. $c^*_-$ is characterized as the smallest c for which (9) has a solution of the form $w(x,t)=e^{-{s}[-x-ct]}\psi (x)$ with ${s}>0$ and $\psi (x)$ L-periodic.

The statements of this Theorem can also be obtained by using the methods of Berestycki et al. [3–5].

As we shall see, Statement 3 of the Theorem 2.1 greatly simplifies the computation of the spreading speeds.

3 Fickian RDA equations for a periodic patchy environment

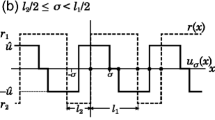
We consider a periodic patchy environment consisting of favorable and unfavorable patches with size $l_1$ and $l_2$, respectively, and propose the Fickian RDA equation with a logistic growth function as below:

$$\begin{aligned} \frac{\partial n}{\partial t}= \frac{\partial }{\partial x}\left( D(x)\frac{\partial n}{\partial x} \right) -\frac{\partial u(x)n}{\partial x} + (r(x)-\mu n)n \end{aligned}$$

(10a)

where

$$\begin{aligned}&D(x)=\left\{ \begin{array}{ll} d_1\ (0 \le x -x_{m} <l_1)\\ d_2\ (l_1 \le x - x_{m} < L) \end{array} \right. ,\ r(x)=\left\{ \begin{array}{ll} r_1\ (0 \le x -x_{m} <l_1)\\ r_2\ (l_1 \le x - x_{m} < L) \end{array} \right. ,\ \nonumber \\&\quad \, x_{m}=mL,\ L=l_1+l_2\ (m=0,\pm 1,\pm 2,\ldots ) \end{aligned}$$

(10b)

$x_{m}$ indicate the left boundaries of the favorable patch located between mL and $mL+l_1$. The diffusion coefficient D(x) and the intrinsic growth rate r(x) are $d_1\,(>0)$ and $r_1\,(>0)$ in the favorable patch and $d_2\,(>0)$ and $r_2\,(<r_1)$ in the unfavorable patch, respectively. u(x) represents the advection velocity at position x, which means that organisms move right or left at speed |u(x)| when u(x) is positive or negative, respectively. In general, the functional form of u(x) may change with species depending on by what means and how far they sense the favorability of environments. As mentioned in the introduction, here we focus on the gradient-based taxis as given by

$$\begin{aligned} u(x) = \alpha \frac{df(x)}{dx}, \end{aligned}$$

where f(x) is the favorability of an environment at x and $\alpha$ the taxis sensitivity.

As a simple and mathematically tractable candidate for f(x), we adopt the intrinsic growth rate $r(x):=R(x,0)$ [2, 9, 37]. Thus the advection velocity function is written as

$$\begin{aligned} u(x) = \alpha \frac{dr(x)}{dx}. \end{aligned}$$

(11)

Because the functions $D'(x)$, u(x) and $r'(x)$ do not satisfy the assumptions of Hypotheses 2.1.i, ii and Remark below Hypotheses 2.1, maximum principle methods cannot be used to define the spreading speed and PTW. Instead, we define the spreading speed and PTW of the problem (10) as the limits as $h\rightarrow 0$ of the the corresponding quantities for the one-parameter family

$$\begin{aligned} \frac{\partial \tilde{n}}{\partial t}= \frac{\partial }{\partial x}\left( \tilde{D}(x)\frac{\partial \tilde{n}}{\partial x} \right) -\frac{\partial \tilde{u}(x)\tilde{n}}{\partial x} + (\tilde{r}(x)-\mu \tilde{n})\tilde{n} \end{aligned}$$

(12a)

where

$$\begin{aligned}&\tilde{D}(x)=\left\{ \begin{array}{cl} \dfrac{d_1-d_2}{2h}(x-x_{m})+\dfrac{d_1+d_2}{2}\ \ \ \ \ \ \ &{}(-h \le x - x_{m} < h)\\ d_1\ &{}(h \le x - x_{m} < l_1-h)\\ \dfrac{d_{2}-d_{1}}{2h}(x-x_{m}-l_1)+\dfrac{d_1+d_2}{2}\ &{}(l_1-h \le x - x_{m} < l_1+h)\\ d_2\ &{}(l_1+h \le x - x_{m} < L-h) \end{array} \right. ,\ \end{aligned}$$

(12b)

$$\begin{aligned}&\tilde{r}(x)=\left\{ \begin{array}{cl} \dfrac{r_1-r_2}{2h}(x-x_{m})+\dfrac{r_1+r_2}{2}\ \ \ \ \ &{}(-h \le x - x_{m} < h)\\ r_1\ &{}(h \le x - x_{m} < l_1-h)\\ \dfrac{r_{2}-r_{1}}{2h}(x-x_{m}-l_1)+\dfrac{r_1+r_2}{2}\ &{}(l_1-h \le x - x_{m} < l_1+h)\\ r_2\ &{}(l_1+h \le x - x_{m} < L-h) \end{array} \right. ,\ \end{aligned}$$

(12c)

$$\begin{aligned}&\tilde{u}(x) = \alpha \dfrac{d\tilde{r}}{dx} = \left\{ \begin{array}{cl} \dfrac{\alpha (r_1-r_2)}{2h} &{}(-h \le x - x_{m} < h)\\ 0\ &{}(h < x - x_{m} < l_1-h)\\ \dfrac{\alpha (r_{2}-r_{1})}{2h} &{}(l_1-h \le x - x_{m} < l_1+h)\\ 0\ &{}(l_1+h \le x - x_{m} < L-h) \end{array} \right. , \end{aligned}$$

(12d)

$$\begin{aligned} (m=0,\pm 1,\pm 2,\ldots ),\nonumber \end{aligned}$$

In (12b) and (12c), we proposed a linear spline form for $\tilde{D}(x)$ and $\tilde{r}(x)$, which satisfy Hypotheses 2.1.i and Remark below Hypotheses 2.1. Since D(x), r(x) and u(x) are the limits as $h\rightarrow 0$ of $\tilde{D}(x)$, $\tilde{r}(x)$ and $\tilde{u}(x)$, respectively, we will obtain the solution of (10) as the limit of the solution of (12) when $h\rightarrow 0$. As will be discussed in Sect.  5.1, $\tilde{D}(x)$ and $\tilde{r}(x)$ can be chosen from a more general class of functions.

3.1 Formula for the PTW speed of the Fickian RDA equation

$\tilde{D}(x)$, $\tilde{u}(x)$ and $\tilde{r}(x)$ as defined by (12b), (12d) and (12c) satisfy Hypotheses 2.1.i, ii and Remark below Hypotheses 2.1, respectively, and $R(x,\tilde{n})=\tilde{r}(x)-\mu \tilde{n}$ satisfy Hypotheses 2.1.iii, iv and v, while Hypothesis 2.1.vi holds if the equilibrium state $\tilde{n}=0$ is unstable. Therefore when $\tilde{n}=0$ is unstable, it follows from Theorem 2.1 that the linearized equation of (12) about $\tilde{n}=0$,

$$\begin{aligned} \frac{\partial \tilde{n}}{\partial t}= \frac{\partial }{\partial x}\left( \tilde{D}(x)\frac{\partial \tilde{n}}{\partial x} \right) -\frac{\partial \tilde{u}(x)\tilde{n}}{\partial x} + \tilde{r}(x)\tilde{n}, \end{aligned}$$

(13)

has a rightward PTW solution of speed $\tilde{c}$ in the form,

$$\begin{aligned} \tilde{n}(x,t) = e^{-s(x-\tilde{c}t)}g(x),\quad \text { where } g(x)=g(x+L),\quad \tilde{c} >0\quad \text { and }\quad s>0, \end{aligned}$$

(14)

and the spreading speed $\tilde{c}^*$ of the rightward PTW of (12) is characterized as the slowest speed of the PTW of (13). In the examples of this and the next sections, the functions $\tilde{D}(x)$ and $\tilde{r}(x)$ are even and $\tilde{u}(x)=\alpha \tilde{r}'(x)$ is odd about $x=\ell _1/2$. Then Theorem 2.1 shows that the leftward spreading speed of such a problem is equal to the rightward spreading speed.

Based on the above statement, we derive a rightward PTW solution and its spreading speed from the linearized equation (13) by using (14).

Let us introduce $p(x)=e^{-sx}g(x)$. Then (14) is rewritten as

$$\begin{aligned} \tilde{n}(x,t) = e^{-s(x-\tilde{c}t)}g(x) = e^{s\tilde{c}t}p(x). \end{aligned}$$

(15)

Substituting (15) into (13) yields

$$\begin{aligned}{}[\tilde{D}(x)p'-\tilde{u}(x)p]' = [\tilde{c}s - \tilde{r}(x)]p. \end{aligned}$$

By further introducing the variable $q(x)=\tilde{D}(x)p'-\tilde{u}(x)p$ , we have a system of first order differential equations,

$$\begin{aligned} \left( \begin{array}{c} p'\\ q' \end{array} \right) = \left( \begin{array}{cc} \tilde{u}(x)/\tilde{D}(x) &{} 1/\tilde{D}(x)\\ \tilde{c}s-\tilde{r}(x) &{} 0 \end{array} \right) \left( \begin{array}{c} p\\ q \end{array} \right) . \end{aligned}$$

(16)

Because $p(x)= e^{-sx}g(x)$ and $q(x)=e^{-sx}[\tilde{D}(x)\{g'(x)-sg(x)\}-\tilde{u}(x)g(x)]$, the condition that g(x) is L-periodic is rewritten in terms of p and q,

$$\begin{aligned} \left( \begin{array}{c} p(x+L)\\ q(x+L) \end{array} \right) = e^{-sL} \left( \begin{array}{c} p(x)\\ q(x) \end{array} \right) . \end{aligned}$$

(17)

Thus we only need to solve (16) with (17) for one spatial period. Here we focus on an interval, $(-h, L-h)$, which contains four subintervals, $(-h, h)$, $(h, l_1-h)$, $(l_1-h, l_1+h)$ and $(l_1+h, L-h)$. In the subintervals, $(h, l_1-h)$ and $(l_1+h, L-h)$, all parameters in (16) are constant so that we can obtain the general solutions (see Appendix 3). For the subintervals, $(-h, h)$ and $(l_1-h, l_1+h)$, on the other hand, it is difficult to solve (16) because the coefficients are space dependent. However, by letting h approach zero, we obtain (see Appendix 3)

$$\begin{aligned}&p(0^+) = \left( \frac{d_1}{d_2}\right) ^\frac{\alpha (r_1-r_2)}{d_1-d_2} p(0^-)\quad \text { and }\quad q(0^+)=q(0^-) \end{aligned}$$

(18a)

$$\begin{aligned}&p(l_1^+) = \left( \frac{d_1}{d_2}\right) ^{-\frac{\alpha (r_1-r_2)}{d_1-d_2}} p(l_1^-)\quad \text { and }\quad q(l_1^+)=q(l_1^-) \end{aligned}$$

(18b)

where 0 and $l_1$ are the left and right boundary points of the favorable patch, and $0^+$ and $0^-,$ or $l_1^+$ and $l_1^-$ , denote the limits as x approaches 0 or $l_1$ from right and left, respectively. Taking the consideration of $p(x)=e^{-s\tilde{c}t}\tilde{n}(x)$ and $q(x)=e^{-s\tilde{c}t}(\tilde{D}(x)\partial \tilde{n}/\partial x - \tilde{u}(x)\tilde{n})$, we have the interface conditions,

$$\begin{aligned} \frac{n(0^+)}{n(0^-)} = \left( \frac{d_1}{d_2}\right) ^\frac{\alpha (r_1-r_2)}{d_1-d_2} = \kappa _F\quad \text { and }\quad d_1 \frac{\partial n(0^+)}{\partial x}= d_2 \frac{\partial n(0^-)}{\partial x}, \end{aligned}$$

(19a)

$$\begin{aligned} \frac{n(l_1^+)}{n(l_1^-)} = \left( \frac{d_1}{d_2}\right) ^{-\frac{\alpha (r_1-r_2)}{d_1-d_2}} = \frac{1}{\kappa _F}\quad \text { and }\quad d_2 \frac{\partial n(l_1^+)}{\partial x}= d_1 \frac{\partial n(l_1^-)}{\partial x}. \end{aligned}$$

(19b)

The first equations in (19a) and (19b) indicate the ratios in population densities across the interfaces at $x=0$ and $x=l_1$, respectively. They are inversely related, and thus designated as $\kappa _F$ and $1/\kappa _F$, respectively. Since $\kappa _{F}>1$ always holds when $\alpha (r_1-r_2)>0$, the gradient-based taxis causes a jump in density from unfavorable to favorable patches at the interface. The second equations in (19a) and (19b) represent the continuity in the flux at the interfaces. As special cases, (19a) is reduced to

$$\begin{aligned} \frac{n(0^+)}{n(0^-)} = \exp \left( \frac{\alpha (r_1-r_2)}{D}\right) \quad \text { and }\quad \frac{\partial n(0^+)}{\partial x}= \frac{\partial n(0^-)}{\partial x},\quad \text { when }\,d_1=d_2=D. \end{aligned}$$

(20a)

and

$$\begin{aligned} \frac{n(0^+)}{n(0^-)} = 1\quad \text { and }\quad d_1\frac{\partial n(0^+)}{\partial x}= d_2\frac{\partial n(0^-)}{\partial x},\quad \text { when }\, \alpha =0\quad \text { or }\, r_1=r_2. \end{aligned}$$

(20b)

Now we solve (16) on $(0^-, L^-)$ by combining (17) for $x=0^-$ and the interface conditions (18a) and (18b). Then we have a dispersion relation between the two unknown variables, the speed of the PTW, c, at the limit of $h\rightarrow 0$ and the damping coefficient, s, as below (see Appendix 3),

$$\begin{aligned} s=Q({\uplambda }), \end{aligned}$$

(21a)

where

$$\begin{aligned}&\begin{aligned} Q({\uplambda })&= \frac{1}{L}\mathrm{Cosh}^{-1}\bigg [\cosh (v_1 l_1)\cosh (v_2 l_2) \\&\quad + \frac{1}{2} \bigg ( \kappa _F\frac{d_1 v_1}{d_2 v_2} + \frac{1}{\kappa _F}\frac{d_2 v_2}{d_1 v_1} \bigg ) \sinh (v_1 l_1)\sinh (v_2 l_2) \bigg ], \end{aligned} \end{aligned}$$

(21b)

$$\begin{aligned}&{\uplambda }\!= \!cs,\ \, v_1\!=\!\sqrt{({\uplambda }-r_1)/d_1},\quad v_2\!=\!\sqrt{({\uplambda }-r_2)/d_2}, \quad \kappa _F \!=\! \left( \frac{d_1}{d_2}\right) ^{\frac{\alpha (r_1-r_2)}{d_1\!-\!d_2}}. \qquad \end{aligned}$$

(21c)

When there is a set of $c>0$ and $s>0$ that satisfy (21), c should be the speed of a PTW of (13) at the limit of $h\rightarrow 0$. Theorem 2.1 states that the asymptotic speed $c^*$ is given by the formula $c^*=\min _{s>0} c(s)$.

Then how can we derive the minimum speed? From (21) we have $c= {\uplambda }/s$, which is rewritten as $c = {\uplambda }/ Q({\uplambda })$ by using (21a). Thus the speed of the PTW of (10), is given by

$$\begin{aligned} c^* = \min _{{\uplambda }>0}\frac{{\uplambda }}{Q({\uplambda })}. \end{aligned}$$

(22)

We obtained the minimum value by using a numerical analysis software.

Fig. 1

Traveling periodic waves (PTW) of the Fickian RDA equation when the taxis sensitivity is a $\alpha =0$, b $\alpha =0.5$ and c $\alpha =2$. Other parameters are $d_1=1$, $d_2=1.2$, $r_1=1$, $r_2 = -1$, $l_1=1$, $l_2=0.5$ and $\mu =1$. Any two successive waves taken at time interval $t^*$ are perfectly superimposed when one of them is moved towards the other by a spatial period, $L=l_1+l_2$. $c^*$ is the spreading speed defined by $L/t^*$. The values of t, $t^*$ and $c^*$ are a 139.5, 1.20 and 1.26, b 110.2, 0.96 and 1.58, and c 191.1, 1.69 and 0.89, respectively

3.2 Numerical results

On the basis of the above theoretical study, we next examine how the spatio-temporal patterns of (10) and its spreading speed vary with the parameter values. We first carry out numerical simulations of equation (10) subject to the interface conditions, (19a) and (19b), with various initial distributions localized around the origin.

In Fig. 1, the range expansions on the right half x axis after a sufficiently long time are shown, when $\alpha$ is 0, 0.5 and 2 while the other parameters are fixed as $d_1=1$, $d_2=1.2$, $l_1=1$, $l_2=0.5$, $r_1=1$, $r_2 = -1$ and $\mu =1$. Note that among these parameters, we can set $d_1=r_1=\mu =1$ without loss of generality, because if we nondimenionalize (10) with (11) by putting

$$\begin{aligned}&n'=\dfrac{\mu n}{r_1},\quad t'=r_1t,\quad x'=\sqrt{\dfrac{r_1}{d_1}}x,\quad d'_2=\dfrac{d_2}{d_1},\quad r'_2=\dfrac{r_2}{r_1},\\&l'_1=\sqrt{\dfrac{r_1}{d_1}}l_1,\quad l'_2=\sqrt{\dfrac{r_1}{d_1}}l_2,\quad u'=u\sqrt{r_1d_1}. \end{aligned}$$

and dropping the primes for notational simplicity, the resultant dimensionless equation is given by (10) with $d_1=r_1=\mu =1$ [15]. Figure 1a shows the case without taxis $(\alpha =0)$ in which the population density continuously changes at the interface (i.e., $\kappa _F=1$). In Fig. 1b, c where $\alpha = 0.5$ and 2, respectively, the population density exhibits prominent jumps at interfaces ($\kappa _F=2.5$ for $\alpha = 0.5$ and $\kappa _F=38.3$ for $\alpha = 2$), while the population density within each favorable patch is gently convex or almost flat. Because a PTW of (12) is given by $n := b(x)W (x - c^*t, x)$ in which b(x) is L-preiodic (see (3)) and W(y, x) is nonincreasing in the first variable and L-periodic in the second one (see the statement below Lemma 2.2), a PTW n is nondecreasing in t for each x, and converges to $b(x)\pi _1(x)$ as $t \rightarrow \infty$. Moreover, increasing t by $t^* := L/c^{*}$ gives the graph with x increased by L. We see from Fig.  1 that the solution after a long time has the same properties as mentioned above. In particular, far behind the front, the graph is close to $b(x)\pi _1(x)$. Conversely, we can estimate the time $t^*$ when the graph is shifted by L, and then approximate $c^{*}$ from the formula $c^{*} = L/t^*$.

From these and additional simulations, we also confirm that populations starting from various locally distributed propagules eventually either go to extinction or evolve to a unique PTW depending on parameter values. The condition for successful invasion (namely, $n=0$ is unstable) is given by $Q(0) > 0$, where $Q({\uplambda })$ is defined by (21b, 21c).

Fig. 2

Speeds of PTWs of the Fickian-RDA and Fokker–Planck RDA equations as functions of $\alpha$ for $r_2= 0.5$, 0, $- 0.5$, $-1$, $-2$, $-3$. The other parameters are the same as in Fig. 1. Thick lines are speed $c^*$ of the Fickian RDA equation derived from the dispersion relation (22), and open circles are the asymptotic speeds numerically derived. The large open circles at $\alpha = 0$, 0.5 and 2 for $r_2= -1$ correspond to Fig. 1a–c, respectively. Thin lines and closed circles are the speed of the Fokker–Planck RDA equation corresponding to the thick lines and open circles of the Fickian RDA equation, respectively. The large closed circles at $\alpha = 0$, 0.5 and 2 for $r_2= -1$ correspond to Fig. 4a–c, respectively

Figure 2 illustrates PTW speed $c^*$ as a function of the taxis sensitivity $\alpha$ for $r_2= 0.5$, 0, $- 0.5$, $-1$, $-2$, $-3$ while the other parameters are the same as in Fig. 1. The thick curves are the speeds of the Fickian RDA equation which are analytically derived from (22) with (21), and open circles are the speeds numerically calculated by $L/t^*$. All curves are one-humped. Particularly, when $r_2$ is small, the speed $c^*$ sharply increases at first and then turns to decrease as $\alpha$ is increased. The large open circles indicated at $\alpha = 0$, 0.5 and 2 for $r_2= -1$ correspond to the range expansion patterns in Fig. 1a–c, respectively. In those three figures, the amplitude of variations in the population density between favorable and unfavorable patches increases as $\alpha$ increases. When $\alpha = 0.5$, the population densities in the favorable patch is much higher than the corresponding density in the case of $\alpha = 0$, and the population density in the unfavorable patch still remains at substantial levels though lower than that in the case of $\alpha = 0$. These situations may contribute to the increased speed as seen in Fig. 2. However, when $\alpha = 2$ in Fig. 1c, the population density in the favorable patch becomes close to the carrying capacity $(r_1/\mu =1)$, while that in the unfavorable patch approaches almost zero. In other words, organisms are trapped within the favorable patches so effectively that it would be harder for them to move to the next adjacent unfavorable patch, thereby leading to a decreased speed.

Fig. 3

Contour maps of PTW speed $c^*$ of the Fickian RDA equation on $(d_2, l_2)$ plane when the taxis sensitivity is a $\alpha =0$, b $\alpha =0.5$ and c $\alpha =2$. Other parameters are $d_1=1$, $r_1=1$, $r_2= -1$, $l_1=1$ and $\mu =1$. The thick dotted curves in a and b indicate the boundaries for population persistence, above which invasion fails. The dotted horizontal and vertical lines are the asymptotes of the boundary curves: $l_2=1.09$, $d_2=0.298$ in a and $l_2=1.09$, $d_2=1.51$ in b. Note that the boundary curve shifts rightward, as $\alpha$ increases. The thin vertical line $d_2=1$ indicates the boundary on which $d_2=d_1(=1)$. The open circles in a–c correspond to the speeds of PTWs as shown in Fig. 1a–c, respectively

In order to see the effects of $d_2$ and $l_2$ in a broader range, we further obtain contour maps of $c^*$ on ($d_2$, $l_2$) plane when $\alpha =0$, 0.5, and 2, while other parameters are kept the same as in Fig. 1. Figure 3a shows the results for the case in the absence of taxis (i.e., $\alpha =0$; see Shigesada et al. [39] for detail). The thick dotted curve indicates the boundary for population persistence, above which invasion fails. The boundary curve has both horizontal and vertical asymptotes which are given by lines $l_2=1.09 (\equiv l_2^c)$ and $d_2=0.298$, respectively (see dotted lines). When $l_2>l_2^c$, $c^*$ shows a one-humped curve as $d_2$ increases and becomes zero when $d_2$ reaches a point on the boundary curve. As $\alpha$ increases from zero, the boundary curve shifts rightward, and thus the area for persistence is enlarged. For example, when $\alpha = 0.5$, the vertical asymptote moves to $d_2=1.51$, while the horizontal asymptote is kept the same as $l_2=l_2^c=1.09$ (see Fig. 3b). The PTW solutions for the parameter sets represented by the open circles in Fig. 3a–c correspond to Fig. 1a–c, respectively.

4 Fokker–Planck RDA equation

4.1 Formula for the PTW speed of the Fokker–Planck RDA equation

Here we consider the Fokker–Planck RDA equation with the logistic growth function as

$$\begin{aligned} \frac{\partial n}{\partial t} = \frac{\partial ^2 D(x) n}{\partial x^2} - \frac{\partial u(x)n}{\partial x} + (r(x)-\mu n)n \end{aligned}$$

(23)

where D(x), r(x) are defined by (10b) and u(x) by (11). In a way similar to the case of the Fickian RDA equation described in Sect.  3, we consider a modification of (23) in which D(x), r(x) and u(x) are replaced by $\tilde{D}(x)$, $\tilde{r}(x)$ and $\tilde{u}(x)$ as defined in (12b), (12c) and (12d), respectively,

$$\begin{aligned} \frac{\partial \tilde{n}}{\partial t}= \frac{\partial ^2 \tilde{D}(x)\tilde{n}}{\partial x^2} -\frac{\partial \tilde{u}(x)\tilde{n}}{\partial x} + (\tilde{r}(x)-\mu \tilde{n})\tilde{n} . \end{aligned}$$

(24)

As noted in Sect.  1.1 and Lemma 2.1, the above equation can be converted into a Fickian RDA equation,

$$\begin{aligned} \frac{\partial \tilde{n}}{\partial t}= \frac{\partial }{\partial x}\left( \tilde{D}(x)\frac{\partial \tilde{n}}{\partial x} \right) -\frac{\partial }{\partial x}\{-\tilde{D}'(x)\tilde{n} + \tilde{u}(x)\tilde{n}\} + (\tilde{r}(x)-\mu \tilde{n})\tilde{n} \end{aligned}$$

(25)

where the effective advection velocity due to the Fokker–Plank diffusion, $-\tilde{D}'(x)$, is newly added to the gradient-based taxis velocity, $\tilde{u}(x)$. Thus we can apply the same analyses as done for the Fickian RDA equation (12) to (25) in which the advection velocity $\tilde{u}(x)$ originally present in (24) is replaced by $-\tilde{D}'(x) + \tilde{u}(x)$. As a result, we have the interface conditions corresponding to (19a) and (19b) in the Fickian RDA equation (see Appendix 4),

$$\begin{aligned} \frac{n(0^+)}{n(0^-)} = \frac{d_2}{d_1}\left( \frac{d_1}{d_2}\right) ^{\frac{\alpha (r_1-r_2)}{d_1-d_2}}=\kappa _r,\quad \ d_1\frac{\partial n(0^+)}{\partial x}= d_2\frac{\partial n(0^-)}{\partial x}, \end{aligned}$$

(26a)

and

$$\begin{aligned} \frac{n(l_1^+)}{n(l_1^-)} = \frac{d_1}{d_2}\left( \frac{d_2}{d_1}\right) ^{\frac{\alpha (r_1-r_2)}{d_1-d_2}}=\frac{1}{\kappa _r},\quad \ d_2\frac{\partial n(l_1^+)}{\partial x}= d_1\frac{\partial n(l_1^-)}{\partial x}, \end{aligned}$$

(26b)

where $\kappa _r$ represents the density jump at the interface in the Fokker–Planck RDA model, which is equal to $(d_2/d_1)\kappa _F$. $(d_2/d_1)$ comes from the effective advection caused by the Fokker–Planck diffusion based on local environmental information (see Appendix 4). Although $\kappa _F>1$ always holds, $\kappa _r$ could be either larger or smaller than one depending on the value of $\alpha (r_1-r_2)/(d_1-d_2)$. Particularly, when $\alpha =0$ or $r_1=r_2$, we have

$$\begin{aligned} \frac{n(0^+)}{n(0^-)} = \frac{n(l_1^-)}{n(l_1^+)} = \frac{d_2}{d_1}, \end{aligned}$$

(27)

which means that even in the absence of taxis, discontinuity in population density appears when $d_1$ is not equal to $d_2$, in contrast to (20b) in the Fickian RDA model where density jump does not occur.

The formula for the PTW speed of the Fokker–Planck RDA equation is given by (21) and (22) in which the equation for $\kappa _F$ in (21c) is replaced by $\kappa _r$.

4.2 Numerical results

We first carry out numerical simulations of the Fokker–Planck RDA equation (23) with (26) and again confirm that initially localized populations eventually either go to extinction or evolve to a unique PTW depending on parameter values. The boundary curve for species persistence is given by $Q(0)=0$, where $Q({\uplambda })$ is defined by (21b) and (21c) in which $\kappa _F$ is substituted by $\kappa _r$.

Figure 4a–c show the PTW solutions of the Fokker–Planck RDA equation with the same parameter sets as used in Fig. 1a–c, respectively. In Fig. 4a where $\alpha =0$, there appears density jump at the interface with ratio $\kappa _r=d_2/d_1=1.2$ so that the amplitude of variations in the population density between the favorable and unfavorable patches is larger than in Fig. 1a where the density changes continuously at the interface. When $\alpha =0.5$ and 2, the density jump is increased to $\kappa _r=3.0$ and 46.0, which are 1.2 times larger than the corresponding $\kappa _F$s, though their spatio-temporal patterns are qualitatively similar to those in Fig. 1b, c, respectively. In Fig. 2, speed $c^*$ as a function of $\alpha$ for the Fokker–Planck RDA model is shown by the thin curves with closed circles. Comparing these thin curves with the thick ones for the Fickian RDA model, we can see that, for each $r_2$, the thin curve is higher than the thick one at $\alpha =0$, whereas this relation is reversed when $\alpha$ exceeds around 0.5. This may be explained in such a way that since $\kappa _r$ is $d_2/d_1(=1.2)$ times higher than $\kappa _F$, organisms with the Fokker–Planck diffusion are more strongly attracted to the favorable patches than those with the Fickian diffusion at sufficiently large $\alpha$, resulting in decelerated speeds compared with the speeds of the Fickian RDA model.

Fig. 4

PTWs of the Fokker–Planck RDA equation when the taxis sensitivity is a $\alpha =0$, b $\alpha =0.5$ and c $\alpha =2$. The other parameters are the same as those used in Fig. 1 for the corresponding Fickan RDA equation. The values of t, $t^*$ and $c^*$ are a 129.0, 1.10 and 1.36, b 111.1, 0.96 and 1.56, and c 201.5, 1.78 and 0.84, respectively

Fig. 5

Contour maps of PTW speed $c^*$ of the Fokker–Planck RDA equation on $(d_2, l_2)$ plane when the taxis sensitivity is a $\alpha =0$, b $\alpha =0.5$ and c $\alpha =2$. The other parameters are the same as in Fig. 3. The thick dotted curve in a indicates the boundary for population persistence, above which invasion fails. As $\alpha$ increases, the boundary curve approaches the y-axis, and vanishes when $\alpha \ge 0.35$. On the thin vertical line $d_2=1$ where $d_2=d_1(=1)$, the speed exactly coincides with that of the corresponding Fickian RDA equation (cf., speeds on the vertical lines in Figs. 3a, 5a). The closed circles in a–c correspond to the speeds of the PTWs shown in Fig. 4 a–c, respectively. Similarly, the open squares in a–c correspond to the PTW speeds shown in Fig. 6 a–c, respectively

Figure 5a–c show contour maps of $c^*$ on $(d_2, l_2)$ plane, in which all parameters are the same as in the corresponding Fickian RDA model used in Fig. 3a–c. The closed circles in a–c correspond to the speeds of the PTWs shown in Fig. 4a–c, respectively. When $\alpha =0$ (Fig. 5a), the boundary curve for persistence appears in the upper left corner (thick dotted line). Note that, on the thin vertical lines where $d_2=1$ (i.e. $d_1=d_2=1$), the speeds exactly coincide between the Fokker–Planck RDA and Fickian RDA models, because $\kappa _F = \kappa _r=1$. In the region where $d_2 <1$ and hence $\kappa _F > \kappa _r$, the speed $c^*$ of the Fokker–Planck RDA model (Fig. 5a) is lower than that of the Fickian RDA model (see Fig. 3a), and vice versa where $d_2>1$. Consequently, the area for population persistence in the region where $d_2 <1$ is smaller in the Fokker–Planck RDA model than in the Fickian RDA model, and vice versa where $d_2 >1$. As $\alpha$ increases from 0, the boundary curve for persistence (thick dotted line) approaches the y-axis, and vanishes when $\alpha \le 0.35$ so that the species becomes able to survive for any positive set of $(d_2, l_2)$. On the other hand, the area for non-persistence in the Fickian RDA model moves to the right as $\alpha$ increases, as mentioned before (Fig. 3b, c). Moreover, the above inequality relations in speed $c^*$ between the two models when $\alpha =0$ become not necessarily true. For example, in Fig. 5c (i.e., at $\alpha =2$), speed $c^*$ of the Fokker–Planck RDA model is higher than that of the Fickian RDA model (Fig. 3c) when $d_2 < 1$, and vice versa if otherwise.

Fig. 6

PTWs of the Fokker–Planck RDA equation when $d_2=0.8$ and the taxis sensitivity is a $\alpha =0$, b $\alpha =0.5$ and c $\alpha =2$, while other parameters are the same as in Fig. 4. In a, the population density is higher in the unfavorable patch than in the unfavorable patch. However, as the taxis sensitivity $\alpha$ is increased to 0.5 and 2, PTWs exhibit patterns qualitatively similar to those in Fig. 4b, c. The values of t, $t^*$ and $c^*$ are a 175.6 1.49 and 1.01, b 124.5, 1.07 and 1.40, and c 257.6, 2.28 and 0.66, respectively

Notably, we found that, in the Fokker–Planck RDA model when $\alpha =0$ and $d_1<d_2$, there appears an unusual pattern such that the population density is higher in the unfavorable patch than in the favorable patch as shown in Fig. 6a, which corresponds to the open square in Fig. 5a. This is mathematically inevitable because the interface condition $\kappa _r=d_2/d_1=0.8$ is smaller than 1. However, when $\alpha =0.5$ and 2, $\kappa _F$ increases to 3 and 86.8 so that the density jump $\kappa _r= (d_2/d_1)\kappa _F$ exceeds one to reach $\kappa _r=2.4$ and 69.4, respectively. As the result the PTW patterns become qualitatively similar to those in Fig. 4b, c.

Recently, Maciel and Lutscher [24] have investigated the effect of individual movement response to habitat edges (i.e., the interface between favorable and unfavorable patches in the present model) on the population persistence and spatial spread by using a reaction–diffusion equation with D(x) and r(x) as defined in (10b). They adopted two types of boundary conditions entailing discontinuity in density at the interface, which were derived by taking a limit of a random walk with habitat preference in movement direction as below [30]

$$\begin{aligned}&\frac{n(0^+)}{n(0^-)}=\frac{n(l_1^-)}{n(l_1^+)}=\frac{a}{1-a}\sqrt{\frac{d_2}{d_1}}, \end{aligned}$$

(28)

$$\begin{aligned}&\frac{n(0^+)}{n(0^-)}=\frac{n(l_1^-)}{n(l_1^+)}=\frac{a}{1-a}{\frac{d_2}{d_1}}, \end{aligned}$$

(29)

where a and $1- a$ represent the probabilities that an individual at the interface moves to patch 1 and patch 2, respectively. Note that both (28) and (29) apparently differ from the discontinuity conditions in either (19) or (26), presumably because the former are derived on the basis of mechanistic rule about individual movement behavior at $x=0$, whereas the latter are deduced from the diffusion–reaction model with taxis which is induced by the spatial gradient in the growth rate. However, when there is neither gradient-based taxis (i.e., $\alpha =0$) nor biased movement (i.e., $a=0.5$) at the interface, the interface condition in the Fokker–Planck RDA equation as given by (27) exactly coincides with (29) for $a=0.5$, and hence speeds $c^*$ of the two models should be equal to each other when all other parameters are the same. They further examined the effect of a on the spreading speed $c^*$, when patch preference a is a function of $l_2$. Under these conditions, we cannot compare their models with ours as such. Nevertheless, their results seem qualitatively similar to those obtained from the Fokker–Planck RDA equation, but not the Fickian RDA equation, in the present study.

5 Discussion

We have previously studied a Fickian reaction–diffusion equation (i.e., (10) with $u(x)=0$) to investigate the range expansion of invasive species in a periodic patchy environment [19, 39]. There we numerically found a PTW solution and derived a heuristic formula for the speed. Subsequently Weinberger [43] rigorously proved the existence of the PTW for more general class of reaction–diffusion equations (see also, Berestycki et al. [3–5], Liang and Zhao [22]). In this article we extended our previous model to include an advection term while the diffusion term is chosen to be either the Fokker–Planck type or the Fickian type. In Sect. 2, Theorems for the existence of the PTW for general class of reaction–diffusion–advection equations are presented. It is also shown that when the growth function is of logistic type, the method to derive the PTW speed of the RD equation is applicable as such to the extended RDA equations.

When the environment is homogeneous in each patch, the taxis occurs only at the interface of favorable and unfavorable patches, so that discontinuity in population density at the interface crucially influences the PTW speed. More specifically, the taxis acts to increase the PTW speed when the taxis sensitivity is moderate, but it turns to decelerate the speed when the taxis sensitivity becomes too large.

5.1 Interface condition

We assumed in Sects. 3 and 4 that D(x), r(x) and u(x) are the limits as $h\rightarrow 0$ of $\tilde{D}(x)$, $\tilde{r}(x)$ and $\tilde{u}(x)(=-d\tilde{r}(x)/dx)$ as given by the linear spline functions, (12b), (12c) and (12d), and obtained the interface conditions (19) and (26) for the Fickian RDA and the Fokker–Planck RDA models, respectively. However, it should be noted that $\tilde{D}(x)$ and $\tilde{r}(x)$ could take various other functional forms within the region $- h < x < h$ under the conditions that satisfy the Hypotheses 2.1.i, ii and Remark below Hypotheses 2.1. In such cases, the interface condition can generally be obtained by using the following equations (see Appendixes 3 and 4, and also Ovaskainen and Cornell [30])

$$\begin{aligned}&\frac{n(0^+)}{n(0^-)} = \lim _{h\rightarrow 0}\exp \left( {\int _{-h}^h\frac{\tilde{u}(\xi )}{\tilde{D}(\xi )}d\xi }\right) \equiv \kappa _F\quad \text { for the Fickian RDA model}, \end{aligned}$$

(30a)

$$\begin{aligned}&\frac{n(0^+)}{n(0^-)} \!=\! \frac{D(0^-)}{D(0^+)}\lim _{h\rightarrow 0}\exp \left( {\int _{-h}^h\frac{\tilde{u} (\xi )}{\tilde{D} (\xi )}d\xi }\!\right) \!\equiv \!\kappa _r \quad \text { for the Fokker}\!-\!\text {Planck RDA model}.\nonumber \\ \end{aligned}$$

(30b)

The transitions (12b) and (12c) from D(x) to $\tilde{D}(x)$ and r(x) to $\tilde{r}(x)$ for $-h \le x \le h$ can be written as the mollifications

$$\begin{aligned} \tilde{D}(x)&=\int _{-\infty }^{\infty }[1/h]\psi (y/h)D(x-y)dy, \end{aligned}$$

(31a)

$$\begin{aligned} \tilde{r}(x)&=\int _{-\infty }^{\infty }[1/h]\psi (y/h)r(x-y)dy, \end{aligned}$$

(31b)

where

$$\begin{aligned} \psi (x)=\left\{ \begin{array}{cl} 1/2 &{}\text { for } |x| \le 1,\\ 0 &{}\text { for } |x| >1.\end{array} \right. \end{aligned}$$

It is natural to look at the more general problem in which the mollifier uses a more general, and possibly smoother, function $\psi (x)$ which satisfies the conditions

$$\begin{aligned} \psi (x) \ge 0, \psi (x)=0\quad \text { for }\, |x|>1,\quad \text { and }\quad \int _{-1}^{1}\psi (x)dx = 1. \end{aligned}$$

(32)

$\tilde{D}(x)$ and $\tilde{r}(x)$ as defined by (31) with (32) are rewritten as:

$$\begin{aligned} \tilde{D}(x)&= (d_1-d_2)\int _{-1}^{x/h}\psi (s)ds + r_2=(d_1-d_2)\phi (x/h)+d_2, \end{aligned}$$

(33a)

$$\begin{aligned} \tilde{r}(x)&= (r_1-r_2)\int _{-1}^{x/h}\psi (s)ds + d_2=(r_1-r_2)\phi (x/h)+r_2, \end{aligned}$$

(33b)

where

$$\begin{aligned} \phi (x)=\int _{-1}^{x}\psi (s)ds. \end{aligned}$$

Then the gradient-based taxis velocity is given by

$$\begin{aligned} \tilde{u}(x) = \alpha \frac{d\tilde{r}(x)}{dx} =\alpha \frac{r_1-r_2}{h}\phi '(x/h)\ \text { for } -h \le x \le h. \end{aligned}$$

(34)

Substituting (33a) and (34) into (30a), we obtain the interface condition at $x=0$:

$$\begin{aligned} \frac{n(0^+)}{n(0^-)}&= \lim _{h\rightarrow 0}\exp \left( {\int _{-h}^h\frac{\tilde{u}(\xi )}{\tilde{D}(\xi )}d\xi }\right) \\&= \lim _{h\rightarrow 0}\exp \left( {\int _{-h}^h\frac{\alpha (r_1-r_2)\phi '(\xi /h)}{h\{(d_1-d_2)\phi +d_2\}}d\xi }\right) \\&= \exp \left( \frac{\alpha (r_1-r_2)}{d_1-d_2}\int _{-1}^1\frac{\phi '(y)}{\phi (y)+d_2/(d_1-d_2)}dy \right) \\&= \left( \frac{d_1}{d_2}\right) ^{\frac{\alpha (r_1-r_2)}{d_1-d_2}} \!= \kappa _F\quad \text { for the Fickian RDA model.} \end{aligned}$$

Similarly, we use (30b) to have

$$\begin{aligned} \frac{n(0^+)}{n(0^-)}&= \frac{d_2}{d_1}\left( \frac{d_1}{d_2}\right) ^{\frac{\alpha (r_1-r_2)}{d_1-d_2}}\!=\kappa _r,\quad \text { for the Fokker}\!-\!\text {Planck RDA model.}\\ \end{aligned}$$

These interface conditions are exactly the same as (19a) and (26a) in which $\tilde{D}(x)$ and $\tilde{r}(x)$ are given by (12b) and (12d). Accordingly, the numerical results described in Sects. 3.2 and 4.2 stand as such without any change. This fact is true as long as the same regularizations are used for D(x) and r(x), but it may not be true if different regularizations are used.

5.2 Effective advection in the Fokker–Plank reaction–diffusion equation

We have investigated the effects of the gradient-based taxis, by which organisms are driven towards patch with larger r(x) at the interface. As noted in Sects. 1.1 and 4, however, even organisms without the gradient-based taxis can show an effective advection with velocity, $-d D(x)/dx$, if they undergo the Fokker–Planck diffusion, which depends only on local information. Thus let us consider the case that D(x) is a decreasing function of r(x), for instance,

$$\begin{aligned} D(x)=\frac{D_0}{1+\gamma r(x)}, \end{aligned}$$

in analogy to the receptor-binding model used for bacterial chemotaxis [13], where $\gamma$ is sufficiently small to make D(x) be uniformly positive.

Here we again assume that r(x) is given by (10b), which is the limit of $h \rightarrow 0$ of $\tilde{r}(x)$ defined in (12c). Then Fokker–Planck reaction–diffusion equation without taxis term is given by

$$\begin{aligned} \frac{\partial \tilde{n}}{\partial t}&= \frac{\partial ^2 \tilde{D}(x)\tilde{n}}{\partial x^2} + (\tilde{r}(x)-\mu \tilde{n})\tilde{n}, \end{aligned}$$

where $\tilde{D}(x)=D_0/(1+\gamma \tilde{r}(x))$ and the effective advection velocity is $-d\tilde{D}(x)/dx=\dfrac{\gamma }{(1+\gamma \tilde{r}(x))^2}d\tilde{r}(x)/dx$. By substituting 0 to $\tilde{u}(x)$ in (30b), we have the interface condition in density as

$$\begin{aligned} \frac{n(0^+)}{n(0^-)} =\frac{D(0^-)}{D(0^+)}=\frac{1+\gamma r_1}{1+\gamma r_2} \end{aligned}$$

which becomes larger as either $r_1$ increases or $r_2$ decreases. Thus we could obtain accumulated distributions in the favorable patches with discontinuity jumps at the interfaces, despite the absence of an explicit advection term in Fokker–Planck RDA. However, the above model would not be suitable for macroscopic organisms which are capable of probing their surrounding environments and undergo directional movement.

5.3 Remaining problems for future studies

The gradient-taxis model presented in this article is concerned with the case that organisms have a relatively short sensing range at their current position. On the other hand, a higher organism with much longer sensing range may be able to integrate the favorability of environments within its sensing range. Thus we need to develop a model that addresses such long-range taxis.

Another limitation of the present models is that they do not take into account the population pressure which comes from density-dependent diffusion due to repulsion among individuals, which has been known to occur in various kinds of organisms [27, 28, 35]. Since the population density tends to be elevated by the presence of taxis as seen in Figs. 1b, c and 2b, c, the population pressure would have important effects. Thus we have been trying to extend our model to incorporate the population pressure.

Other remaining problems include extensions of the reaction–diffusion–advection model in heterogeneous environments to a two-dimensional space, incorporation of the Allee effect [10, 16, 20, 32, 42], multiple-species interactions [7, 11, 25, 26] and so on, toward further understanding of how taxis influences the spatio-temporal pattern and the spreading speed of the periodic traveling wave under more realistic ecological contexts.

Appendices

Appendix 1: Proof of Lemma 2.1

We substitute $n(x,t)=b(x)v(x,t)$ into Eq. (1) and divide by b(x) to see that

$$\begin{aligned} v_t-Dv_{xx}-\left\{ D' +u+\frac{2[Db'-ub]}{b}\right\} v_x-\{[Db'-ub]'+R(x,bv)\}v=0. \end{aligned}$$

(35)

Differentiation of the definition (3) shows that

$$\begin{aligned} Db'-ub=-1+e^{-\int _0^L [u(y)/D(y)]dy} \end{aligned}$$

(36)

which is a constant. We substitute this formula into (35) to obtain the equation

$$\begin{aligned} v_t-Dv_{xx}-\{D'+u+2\frac{-1+e^{-\int _0^L[u(y)/D(y)]dy}}{b(x)} \}v_x-R(x,bv)v=0. \end{aligned}$$

This verifies Eq. (6) with the definitions (7).

It is easily seen that

$$\begin{aligned} b(0)=b(L)=\int _0^L\{e^{\int _0^z [u(y)/D(y)]dy}/D(z)\}dz, \end{aligned}$$

and (36) shows that $b'(0)=b'(L)$. Since D(x) and u(x) are L-periodic, the Eq. (4) shows that b(x) is also L-periodic, so that Lemma 2.1 is proved.

Appendix 2: Proof of Lemma 2.2

The habitat for this problem is the whole real line, so that Hypothesis 2.1.i of Weinberger [43] is satisfied.

The principal tool in verifying the other hypotheses is the well-known Comparison Principle

Comparison Principle

If two functions $v^{(1)}(x,t)$ and $v^{(2)}(x,t)$ have the properties

$$\begin{aligned} \frac{\partial v^{(1)}}{\partial t}&-D(x)\frac{\partial ^2 v^{(1)}}{\partial x^2} -A(x)\frac{\partial v^{(1)}}{\partial x}-f(x,v^{(1)}(x,t)) \\&\le \frac{\partial v^{(2)}}{\partial t}-D(x)\frac{\partial ^2 v^{(2)}}{\partial x^2} -A(x)\frac{\partial v^{(2)}}{\partial x}-f(x,v^{(2)}(x,t)),\\&\qquad v^{(1)}(x,0)\le v^{(2)}(x,0), \end{aligned}$$

and if there is a nonnegative constant M such that

$$\begin{aligned} f(x,v^{(1)})-f(x,v^{(2)}) \le M[v^{(1)} - v^{(2)}]\quad \text { when } v^{(1)} \ge v^{(2)}, \end{aligned}$$

then

$$\begin{aligned} v^{(1)}(x,t)\le v^{(2)}(x,t) \end{aligned}$$

for all $t\ge 0$.

This result follows immediately from applying the maximum principle for parabolic equations to the function $e^{Mt-x^2}[v^{(1)}(x,t)-v^{(2)}(x,t)]$ (see, e.g., Theorems 7 and 10 of Chapter 3 of Protter and Weinberger [33]).

A special case of the Comparison Principle is the fact that if $0\le v^{(1)}(x,0)\le v^{(2)}(x,0)$, for two solutions of (6), then $0\le v^{(1)}(x,1)\le v^{(2)}(x,1)$ (Note that Hypotheses 2.1.iv and v and the definition (7) of S(x, v) show that if $v^{(1)} \ge v^{(2)}$, then

$$\begin{aligned} S(x,v^{(1)})v^{(1)}-S(x,v^{(2)})v^{(2)}&\le S(x,v^{(2)})[v^{(1)}-v^{(2)}]\\&\le \max _x \{R(x, 0)\}[v^{(1)}-v^{(2)}]. \end{aligned}$$

By definition, this states that if $0\le u^{(1)}(x)\le u^{(2)}(x)$, then

$$\begin{aligned} 0\le Q[u^{(1)}(\cdot )](x)\le Q[u^{(2)}(\cdot )](x). \end{aligned}$$

That is, Q is order-preserving, which is the second hypothesis in Weinberger [43].

The lattice $\mathcal L$ of Hypothesis 2.1.iii of Weinberger [43] consists of the set of translations by integral multiples of L, and P is the interval [0, L).

To verify Hypothesis 2.1.iv of Weinberger [43], we first define the function

$$\begin{aligned} \pi _0(x)\equiv 0, \end{aligned}$$

and observe that it is an equilibrium of the Eq. (6).

We define the function

$$\begin{aligned} z(x):=\ell (x)/b(x), \end{aligned}$$

where $\ell (x)$ is the function in Hypothesis 2.1.vi and b(x) is the function (3). This change of variable takes the hypothesis into the condition that z(x) is uniformly bounded, uniformly positive, and L-periodic, and that

$$\begin{aligned} D(x)z''+A(x)z'+S(x,0)z\ge \gamma z. \end{aligned}$$

We also observe that by Hypothesis 2.1.v

$$\begin{aligned} S(x,v)\ge S(x,0)-m\; b(x)\; v \ge S(x,0)-\hat{m}\, v, \end{aligned}$$

(37)

where

$$\begin{aligned} \hat{m}:=m\, \displaystyle {\max _x}\{b(x)\}. \end{aligned}$$

The function

$$\begin{aligned} \hat{v}=\epsilon e^{[\gamma /2] t}z(x), \end{aligned}$$

where $\epsilon$ is positive and small, satisfies the inequality

$$\begin{aligned} \frac{\partial \hat{v}}{\partial t}&-D(x)\frac{\partial ^2\hat{v}}{\partial x^2}- A(x)\frac{\partial \hat{v}}{\partial x}-S(x,\hat{v})\hat{v} \\&\quad \le \epsilon e^{[\gamma /2]t}\left\{ \frac{\gamma }{2}z - [Dz''+Az'+S(x,0)z]\right\} +\epsilon ^2 e^{\gamma t}\hat{m} \; z^2 \\&\quad \le -\epsilon e^{[\gamma /2]t}z\left\{ \frac{\gamma }{2}-\epsilon e^{[\gamma /2]t}\hat{m} \; z\right\} . \end{aligned}$$

We choose $\epsilon$ so small that the last factor is negative for $0\le t\le 1$. The Comparison Principle then shows that the solution v(x, t) of (6) with $v(x,0)=\epsilon z(x)$ is bounded below by $\epsilon e^{[\gamma /2]t} z(x)$. In particular,

$$\begin{aligned} Q[\epsilon z(\cdot )](x)\ge \epsilon e^{[\gamma /2]t} z(x)>\epsilon z(x). \end{aligned}$$

The Comparison Principle shows that v(x, n) is nondecreasing in n.

The Comparison Principle also shows that if $\epsilon$ is so small that $\epsilon z(x)\le \bar{n} /$ $\min _x\{b(x)\}$, where $\bar{n}$ is the constant in Hypothesis 2.1.iii, then $v(x,n)\le \bar{n}/\min _x$ $\{b(x)\}$, which is uniformly bounded. Standard results on solutions of parabolic equations show that solutions of (6) have smoothness properties including equicontinuity. Therefore, the bounded increasing sequence of L-periodic functions v(x, n) converges to a positive continous L-periodic function, which we denote by $\pi _1(x)$. It is an equilibrium of the recursion (8), and also of the Eq. (6).

The strong maximum principle shows that if the initial values of a solution v of (6) are nonnegative, then $v(x,t)>0$ for $t>0$. If the initial function is also L-periodic, then v(x, t) is L-periodic in x. Therefore, v(x, 1) is bounded below by a multiple of $\epsilon z(x)$ with $\epsilon >0$, so that if $\pi _0=0\le v(x,0)\le \pi _1(x)$ then v(x, t) must converge to $\pi _1(x)$. Thus Hypothesis iv of Weinberger [43] is valid.

The standard results we have mentioned above also give the remaining two Hypotheses 2.1, so these Hypotheses follow from our Hypotheses 2.1.

Corollary 2.1 of Weinberger [43] requires additional conditions on the time-1 map M of the linearization

$$\begin{aligned} \frac{\partial w}{\partial t}-D(x)\frac{\partial ^2 w}{\partial x^2} -A(x)\frac{\partial w}{\partial x}-S(x,0)w=0. \end{aligned}$$

(38)

of (6). Two conditions are required. Because Hypothesis 2.1.v makes

$$\begin{aligned} S(x,0)\ge S(x,w), \end{aligned}$$

the Comparison Principle states that if the initial values of a solution v of (6) and w of (38) are both $v_0(x)$, then

$$\begin{aligned} v(x,t)\le w(x,t). \end{aligned}$$

Setting $t=1$ gives the condition

$$\begin{aligned} Q[v_0(\cdot )](x)\le M[v_0(\cdot )]. \end{aligned}$$

This is one of the conditions of Corollary 2.1.

The other significant condition is that for any $\delta >0$ $Q[v_0]\ge [1-\delta ] M[v_0]$ if $0\le t\le 1$ and $v_0$ is sufficiently small. This is implied by the statement that if $v(x,0)=w(x,0)=v_0$ and if $v_0$ is small, then

$$\begin{aligned} v(x,t)\ge [1-\delta ]w(x,t)\quad \mathrm{for}\, 0\le t\le 1. \end{aligned}$$

Since (37) holds, the solution v of (6) is bounded below by the solution q of the equation

$$\begin{aligned} \frac{\partial q}{\partial t}-D(x)\frac{\partial ^2 q}{\partial x^2} -A(x)\frac{\partial q}{\partial x}-[S(x,0)-\hat{m} q]q = 0 \end{aligned}$$

with the same initial conditions. Since $\hat{m} q\ge 0$, $q(x,t)\le w(x,t)$. The Comparison Principle shows that if

$$\begin{aligned} w(x,0)=v_0(x) \le \epsilon , \end{aligned}$$

then

$$\begin{aligned} w(x,t) \le \epsilon e^{\max _x\{S(x,0)\}t}. \end{aligned}$$

Thus, if we define

$$\begin{aligned} \beta :=e^{\max _x\{S(x,0)\}}, \end{aligned}$$

we see that

$$\begin{aligned} q(x,t) \le v(x,t) \le w(x,t) \le \epsilon \beta \quad \mathrm{for }\ 0 \le t \le 1. \end{aligned}$$

We use this inequality in the term $\hat{m}q$ in the equation for q to see that

$$\begin{aligned} \frac{\partial q}{\partial t}-D(x)\frac{\partial ^2 q}{\partial x^2} -A(x)\frac{\partial q}{\partial x}-[S(x,0)-{\hat{m}}\beta \epsilon ]q \ge 0\quad \mathrm{for}\, 0 \le t \le 1. \end{aligned}$$

Thus the Comparison Principle shows that

$$\begin{aligned} v(x,t)\ge q(x,t) \ge e^{-\hat{m} \beta \epsilon t}w(x,t)\quad \mathrm{for}\, 0\le t\le 1. \end{aligned}$$

We set $t=1$ to see that

$$\begin{aligned} Q[v_0]\ge e^{-\hat{m} \beta \epsilon }M[v_0]\quad \mathrm{when}\, 0\le v_0\le \epsilon . \end{aligned}$$

Since $e^{-\hat{m} \beta \epsilon }\ge 1-\delta$ when $\epsilon$ is sufficiently small, this completes the proof of Lemma 2.2.

Appendix 3: Derivation of (18) and (21)

Consider (16) with (12b), (12c) and (12d) in one spatial period, $(-h,\, L-h)$:

$$\begin{aligned}&\frac{dp}{dx}=\frac{\tilde{u}(x)}{\tilde{D}(x)}p(x) + \frac{q(x)}{\tilde{D}(x)} , \end{aligned}$$

(39a)

$$\begin{aligned}&\frac{dq}{dx}=[\tilde{c} s - \tilde{r}(x)]p(x) . \end{aligned}$$

(39b)

Since the interval $(-h, L-h)$ consists of four subintervals, $(-h, h)$, $(h, l_1-h)$, $(l_1-h, l_1+h)$ and $(l_1+h, L-h)$, we first solve (39) for each subinterval. If we have a relation between (p(b), q(b)) and (p(a), q(a)) in any one of the subintervals (a, b) in the form

$$\begin{aligned} \left( \begin{array}{c} p(b) \\ q(b) \end{array} \right) = A^{(a,b)} \left( \begin{array}{c} p(a) \\ q(a) \end{array} \right) , \end{aligned}$$

then the relation in the interval $(-h, L-h)$ is given by

$$\begin{aligned} \left( \begin{array}{c} p(L-h) \\ q(L-h) \end{array} \right) = A^{(l_1+h,L-h)} A^{(l_1-h,l_1+h)} A^{(h,l_1-h)} A^{(-h,h)} \left( \begin{array}{c} p(-h) \\ q(-h) \end{array} \right) . \end{aligned}$$

(40)

On the other hand, (17) for $x= -h$ gives

$$\begin{aligned} \left( \begin{array}{c} p(L-h) \\ q(L-h) \end{array} \right) = e^{-sL} \left( \begin{array}{c} p(-h) \\ q(-h)\end{array} \right) . \end{aligned}$$

(41)

By letting h approach zero in (40) and (41) and combining the resulting equations, we obtain

$$\begin{aligned} A^{(l_1^+,L^-)} A^{(l_1^-,l_1^+)} A^{(0^+,l_1^-)} A^{(0^-,0^+)} \left( \begin{array}{c} p(0^-) \\ q(0^-) \end{array} \right) = e^{-sL} \left( \begin{array}{c} p(0^-) \\ q(0^-) \end{array} \right) . \end{aligned}$$

Thus, the following dispersion relation between speed c of a PTW and the damping coefficient s should hold

$$\begin{aligned} \det \left[ A^{(l_1^+,L^-)} A^{(l_1^-,l_1^+)} A^{(0^+,l_1^-)} A^{(0^-,0^+)} - e^{-sL} I\right] =0. \end{aligned}$$

(42)

Now we calculate $A^{(a,b)}$ for each subinterval. In the subintervals, $(h,l_1-h)$ and $(l_1+h,L-h)$, all the parameters in (39) are constant and $\tilde{u}(x)=0$ so that we can easily obtain

$$\begin{aligned} \lim _{h\rightarrow 0} A^{(h,l_1-h)}= & {} \lim _{h\rightarrow 0} F(d_1, \sqrt{(\tilde{c}s-r_1)/d_1}, l_1-2h) \nonumber \\= & {} F(d_1, \sqrt{(\tilde{c}s-r_1)/d_1}, l_1), \end{aligned}$$

(43a)

$$\begin{aligned} \lim _{h\rightarrow 0} A^{(l_1+h,L-h)}= & {} \lim _{h\rightarrow 0} F(d_2, \sqrt{(\tilde{c}s-r_2)/d_2}, l_2-2h)\nonumber \\= & {} F(d_2, \sqrt{(\tilde{c}s-r_2)/d_2}, l_2), \end{aligned}$$

(43b)

where

$$\begin{aligned}&F(D,v,\ell )=\left( \begin{array}{cc} \cosh v \ell &{} \dfrac{1}{Dv}\sinh v \ell \\ Dv \sinh v \ell &{} \cosh v \ell \end{array} \right) . \end{aligned}$$

Multiplying the both sides of (39a) by $\exp \left( -\displaystyle {\int _{-h}^x \dfrac{\tilde{u}(\xi )}{\tilde{D}(\xi )} d\xi } \right)$ and rearranging them yields

$$\begin{aligned} \frac{d}{dx}\left[ p(x)\exp \left( -\displaystyle {\int _{-h}^x \dfrac{\tilde{u}(\xi )}{\tilde{D}(\xi )} d\xi } \right) \right] = \frac{q(x)}{\tilde{D}(x)}\exp \left( -\displaystyle {\int _{-h}^x \dfrac{\tilde{u}(\xi )}{\tilde{D}(\xi )} d\xi } \right) . \end{aligned}$$

(44)

Then integrating the both sides of (44) over $(-h, h)$ leads to

$$\begin{aligned} p(h)\exp \left( -\displaystyle {\int _{-h}^h \dfrac{\tilde{u}(\xi )}{\tilde{D}(\xi )} d\xi } \right) {-}p(-h) = \int _{-h}^h \frac{q(x)}{\tilde{D}(x)}\exp \left( {-}\displaystyle {\int _{-h}^x \dfrac{\tilde{u}(\xi )}{\tilde{D}(\xi )} d\xi } \right) dx. \end{aligned}$$

(45)

Since

$$\begin{aligned} \int _{-h}^h \dfrac{\tilde{u}(\xi )}{\tilde{D}(\xi )} d\xi&=\frac{\alpha (r_1-r_2)}{d_1-d_2} \log \frac{d_1}{d_2}, \end{aligned}$$

and the right-hand side of (45) is in the order of O(h), we have

$$\begin{aligned} p(h)= p(-h)\exp \left( \displaystyle {\int _{-h}^h \dfrac{\tilde{u}(\xi )}{\tilde{D}(\xi )} d\xi } \right) + O(h) = p(-h)\left( \frac{d_1}{d_2}\right) ^{\frac{\alpha (r_1-r_2)}{d_1-d_2}} + O(h). \end{aligned}$$

(46)

Similarly, integrating the both sides of (39b) over $(-h, h)$, we have

$$\begin{aligned} q(h)= q(-h) + O(h). \end{aligned}$$

(47)

(46) and (47) are reduced to (18a) when $h \rightarrow 0$. It follows from (15) that (19a) also holds. Thus we have

$$\begin{aligned} \lim _{h\rightarrow 0}A^{(-h,h)} = \left( \begin{array}{cc} \kappa _F &{} 0 \\ 0 &{} 1 \end{array} \right) , \quad \text {where} \, \kappa _F=\left( \frac{d_1}{d_2}\right) ^{\frac{\alpha (r_1=r_2)}{d_1-d_2}}. \end{aligned}$$

(48)

As for the interval, $(l_1-h, l_1+h)$, the same procedure as for the interval $(-h, h)$ is applied to give

$$\begin{aligned} \lim _{h\rightarrow 0}A^{(l_1-h,l_1+h)} = \left( \begin{array}{cc} 1/\kappa _F &{} 0 \\ 0 &{} 1 \end{array} \right) . \end{aligned}$$

(49)

Substituting (43), (48) and (49) into (42), we have the dispersion relation (21).

Appendix 4: Derivation of (26)

Consider the linearized equation of (25),

$$\begin{aligned} \frac{\partial \tilde{n}}{\partial t} = \frac{\partial }{\partial x}\left( \tilde{D}(x)\frac{\partial \tilde{n}}{\partial x} \right) - \frac{\partial }{\partial x}\{[- \tilde{D}'(x) + \tilde{u}(x)] \tilde{n}\} + \tilde{r}(x) \tilde{n}, \end{aligned}$$

(50)

where $\tilde{D}(x)$, $\tilde{r}(x)$ and $\tilde{u}(x)$ are defined by (12b), (12c) and (12d), respectively. Since the advection velocity, $-\tilde{D}'(x) + \tilde{u}(x)$, is uniformly bounded, all properties in Hypotheses 2.1 are satisfied if the equilibrium state $\tilde{n}=0$ is unstable. Thus we can apply the same method as used in Sect. 3.1 to (50) to have the interface conditions and the speed of the PTW.

Following (15), we put $\tilde{n}(x,t)=e^{-s(x-\tilde{c}t)}g(x)=e^{s\tilde{c} t}p(x)$ as a PTW solution of (50). Then we have the same equations as (16) and (17), in which $\tilde{u}(x)$ is replaced by $-\tilde{D}'(x) + \tilde{u}(x)$. Thus, substituting $-\tilde{D}'(x) + \tilde{u}(x)$ into $\tilde{u}(x)$ in (46) of Appendix 3, we obtain

$$\begin{aligned} p(h)= p(-h)\exp \left( \displaystyle {\int _{-h}^h \dfrac{-\tilde{D}'(\xi )+\tilde{u}(\xi )}{\tilde{D}(\xi )} d\xi } \right) + O(h). \end{aligned}$$

By using $n(h)=e^{s \tilde{c} t}p(h)$ in (15), we have the interface condition at $x=0$ as the limit when $h\rightarrow 0$,

$$\begin{aligned} \frac{n(0^+)}{ n(0^-)}&=\lim _{h \rightarrow 0}\frac{p(h)}{ p(-h)} =\lim _{h \rightarrow 0}\exp \left( \displaystyle {\int _{-h}^h \dfrac{-\tilde{D}'(\xi )+\tilde{u}(\xi )}{\tilde{D}(\xi )} d\xi } \right) \\&= \lim _{h \rightarrow 0}\exp \left( \displaystyle {-\log \dfrac{\tilde{D}(h)}{\tilde{D}(-h)}} \right) \exp \left( \displaystyle {\int _{-h}^h \dfrac{\tilde{u}(\xi )}{\tilde{D}(\xi )} d\xi } \right) \\&= \dfrac{ D(0^-)}{ D(0^+)} \lim _{h \rightarrow 0}\exp \left( \displaystyle {\int _{-h}^h \dfrac{\tilde{u}(\xi )}{\tilde{D}(\xi )} d\xi } \right) \\&= \frac{d_2}{d_1}\left( \frac{d_1}{d_2}\right) ^{\frac{\alpha (r_1-r_2)}{d_1-d_2}} \equiv \kappa _r. \end{aligned}$$

In a similar manner as in Appendix 3, the dispersion relation is given by (42) in which $\kappa _F = (d_1/d_2)^{\frac{\alpha (r_1-r_2)}{d_1-d_2}}$ is replaced by $\kappa _r = (d_2/d_1)(d_1/d_2)^{\frac{\alpha (r_1-r_2)}{d_1-d_2}}$.