Dynamical behavior of a delay differential equation system on toxin producing phytoplankton and zooplankton interaction

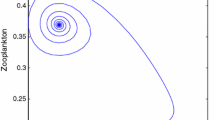
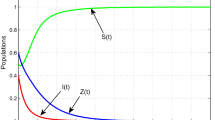
Abstract

In this paper, a toxin producing phytoplankton–zooplankton system with the delay is investigated. Firstly, the nonnegativity and boundedness of solutions are given. Then the local and global asymptotic stabilities of the boundary equilibrium are investigated, and the existence of local Hopf bifurcations is established as the delay crosses a threshold value at the positive equilibrium. Furthermore, there exists at least one positive periodic solution as the delay varies in some regions by using the global Hopf bifurcation result of Wu for functional differential equations. In addition, the impacts of the toxic substances are also investigated. At last, an explicit algorithm is derived for the stability and direction of the bifurcating periodic solution by using center manifold theory and normal form method.

Appendix: Property of Hopf bifurcation

In this section, based on numerical evaluation of Hopf bifurcations [22], it gives the computing process of the direction of Hopf bifurcations and stability of the bifurcating periodic solutions from $E^*$ under the conditions of Theorem 3.7 (ii). Let $\omega ^0=\omega (\tau ^0)$, $\tau =\tau ^0+\mu$, then $\mu =0$ is a Hopf bifurcation value of the system (1.5). Rewrite (3.10) as

$$\begin{aligned} \begin{pmatrix} \dot{x}(t)\\ \;\\ \dot{y}(t) \end{pmatrix} = B_1 \begin{pmatrix} x(t)\\ \;\\ y(t) \end{pmatrix} + B_2 \begin{pmatrix} x(t-\tau )\\ \;\\ y(t-\tau ) \end{pmatrix}+ G(x(t),y(t),x(t-\tau ),y(t-\tau ))\nonumber \\ \end{aligned}$$

(6.1)

where

$$\begin{aligned} B_{1}=\left( \begin{array}{lc} -P^*+\frac{\gamma _1P^*Z^*}{(1+\gamma _1P^*)^2} &{} \qquad -\frac{ P^*}{1+\gamma _1P^*}\\ \;\\ 0 &{}\qquad -\delta \end{array} \right) , \, \\ B_{2}=\left( \begin{array}{lc} 0 &{} \qquad 0\\ \;\\ (\frac{\beta _1 Z^*}{(1+\gamma _1P^*)^2}-\frac{\rho Z^*}{(1+\gamma _2P^*)^2})e^{-\delta \tau ^0} &{} \qquad \delta \end{array} \right) , \end{aligned}$$

$$\begin{aligned} \begin{array}{ll} G(x(t),y(t),x(t-\tau ),y(t-\tau ))=\\ \;\\ \left( \begin{array}{cc} \Big [\frac{\gamma _1 Z^*}{(1+\gamma _1P^*)^3}-1\Big ]x^2(t)-\frac{1}{2(1+\gamma _1P^*)^2}x(t)y(t)\\ -\frac{\gamma _1^2 z^*}{(1+\gamma _1P^*)^4}x^3(t) +\frac{\gamma _1}{3(1+\gamma _1P^*)^4}x^2(t)y(t)+O(4)\\ \;\\ - e^{-\delta \tau }\Big [\frac{\beta _1\gamma _1 Z^*}{(1+\gamma _1P^*)^3}-\frac{\rho \gamma _2 Z^*}{(1+\gamma _2P^*)^3}\Big ]x^2(t-\tau ) \\ \;\\ + e^{-\delta \tau }\Big [\frac{\beta _1}{2(1+\gamma _1P^*)^2}-\frac{\rho }{2(1+\gamma _2P^*)^2}\Big ]x(t-\tau )y(t-\tau )\\ \;\\ + e^{-\delta \tau }\Big [\frac{\beta _1\gamma _1^2 Z^*}{(1+\gamma _1P^*)^4}-\frac{\rho \gamma _2^2 Z^*}{(1+\gamma _2P^*)^4}\Big ]x^3(t-\tau )\\ \;\\ -e^{-\delta \tau }\Big [\frac{\beta _1\gamma _1 }{3(1+\gamma _1P^*)^4}-\frac{\rho \gamma _2 }{3(1+\gamma _2P^*)^4}\Big ]x^2(t-\tau )y(t-\tau )+O(4) \end{array} \right) , \end{array} \end{aligned}$$

and for $\varphi \in C$, define

$$\begin{aligned} L_{\mu }(\varphi )=B_{1} \begin{pmatrix} \varphi _1(0) \\ \;\\ \varphi _2(0)\end{pmatrix} +B_{2} \begin{pmatrix} \varphi _1(-\tau ) \\ \;\\ \varphi _2(-\tau ) \end{pmatrix}, \end{aligned}$$

where $C=C([-\tau ,0],R_+^2)$ with the norm $|\varphi |=\sup _{-\tau \le \theta \le 0}|\varphi (\theta )|$ is the phase space. Clearly, $L_\mu$ is a linear continuous operator from $C$ to $R_+^2$. By the Riesz representation theorem, there exists a matrix whose components are bounded variation functions $\eta (\theta ,\mu )$ in $\theta \in [-\tau ,0]$ such that

$$\begin{aligned} L_{\mu }\varphi =\int _{-\tau }^0 d\eta (\theta ,\mu )\varphi (\theta ), \end{aligned}$$

(6.2)

where $\varphi \in C.$ In fact, it may choose

$$\begin{aligned} \eta (\theta ,\mu )=B_{1} \delta (\theta )-B_{2} \delta (\theta +\tau ), \end{aligned}$$

where

$$\begin{aligned} \delta (\theta )={\left\{ \begin{array}{ll}1, &{} \theta =0 \\ 0, &{} \theta \ne 0. \end{array}\right. } \end{aligned}$$

For $\varphi \in C^1=C([0,\tau ],(R_+^2)^{*})$ , define

$$\begin{aligned} A(\mu )\varphi =\left\{ \begin{array}{ll} \dot{\varphi }(\theta ), &{}\theta \in [-\tau ,0)\\ \int _{-\tau }^{0}d\eta (s,\mu )\varphi (s),&{}\theta =0, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} R(\mu )\varphi =\left\{ \begin{array}{ll} 0 , &{}\theta \in [-\tau ,0)\\ F(\mu ,\varphi ), &{}\theta =0, \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} F(\mu ,\varphi )= \begin{pmatrix} \Big [\frac{\gamma _1 Z^{*}}{(1+\gamma _{1P}^{*})^{3}}-1\Big ]\varphi _1^2(0)-\frac{1}{2(1+\gamma _{1P}^{*})^{2}}\varphi _1(0)\varphi _2(0)\\ -\frac{\gamma _{1}^{2} z^{*}}{(1+\gamma _{1P}^{*})^{4}}\varphi _{1}^{3(0)} +\frac{\gamma _1}{3(1+\gamma _{1P}^{*})^{4}}\varphi _{1}^{2(0)}\varphi _{2(0)}+O(4)\\ - e^{-\delta \tau }\Big [\frac{\beta _{1}\gamma _{1} Z^{*}}{(1+\gamma _{1P}^{*})^{3}}-\frac{\rho \gamma _{2} Z^{*}}{(1+\gamma _{2P}^{*})^{3}}\Big ]\varphi _{1}^{2(-\tau )} \\ +e^{-\delta \tau }\Big [\frac{\beta _1}{2(1+\gamma _1P^*)^2}-\frac{\rho }{2(1+\gamma _2P^*)^2}\Big ]\varphi _1(-\tau )\varphi _2(-\tau )\\ + e^{-\delta \tau }\Big [\frac{\beta _1\gamma _1^2 Z^*}{(1+\gamma _1P^*)^4}-\frac{\rho \gamma _2^2 Z^*}{(1+\gamma _2P^*)^4}\Big ]\varphi _1^3(-\tau )\\ -e^{-\delta \tau }\Big [\frac{\beta _1\gamma _1 }{3(1+\gamma _1P^*)^4}-\frac{\rho \gamma _2}{3(1+\gamma _2P^*)^4}\Big ]\varphi _1^2(-\tau )\varphi _2(-\tau )+O(4) \end{pmatrix} \end{aligned}$$

is the nonlinear term of the right side of the system (6.1).

Let $u=(x,y)^T ,$ then the system (6.1) can be rewritten as

$$\begin{aligned} \dot{u_t}=A(\mu )u_t+R(\mu )u_t. \end{aligned}$$

(6.3)

For $\psi \in C^1$ , define

$$\begin{aligned} A^*\psi (s)=\left\{ \begin{array}{ll}-\dot{\psi }(s), &{}s\in (0,\tau ]\\ \int _{-\tau }^0d\eta ^T(t,\tau ^*)\psi (-t),&{}s=0, \end{array} \right. \end{aligned}$$

and a bilinear form

$$\begin{aligned} \langle \psi ,\varphi \rangle =\bar{\psi }(0)\varphi (0)- \int _{-\tau }^0\int _0^{\theta }\bar{\psi }(\xi -\theta ) d\eta (\theta )\varphi (\xi )d\xi , \end{aligned}$$

where $\eta (\theta )=\eta (\theta ,\tau ^0).$ Then $A^*$ and $A$ are adjoint operators. In addition, from Sect. 2, we know that $\pm i\omega ^0$ are the eigenvalues of $A(\tau ^0)$. Thus they are also the eigenvalues of $A^*$.

By direct computation, it can obtain that $q(\theta )=\Big (1,\,q_2\Big )e^{i\omega ^0\theta }$ is the eigenvector of $A(0)$ corresponding to $i\omega ^0$; and $q^*(s)=\bar{D}\Big (1,\,q_2^*\Big )^Te^{i\omega ^0 s}$

is the eigenvector $A^*$ corresponding to $-i\omega ^0$, where

$$\begin{aligned} \begin{array}{ll} q_2=-\frac{(i\omega ^0+P^*)(1+\gamma _1P^*)^2-\gamma _1P^*Z^*}{ P^*(1+\gamma _1P^*)},\quad q_2^*=\frac{ P^*}{(1+\gamma _1P^*)(i\omega ^0-\delta +\delta e^{i\omega ^0\tau ^0})}. \end{array} \end{aligned}$$

Moreover,

$$\begin{aligned} \langle q^*(s), q(\theta ) \rangle = 1 ,\quad \langle q^*(s),\bar{q} (\theta ) \rangle = 0 , \end{aligned}$$

where

$$\begin{aligned} \begin{array}{ll} D=\Big \{1+q_2\bar{q}_2^*\Big [1+\tau ^0\delta e^{-i\omega ^0\tau ^0}\Big ]+\tau ^0 e^{-(\delta +i\omega ^0)\tau ^0}\bar{q}_2^*\Big [\frac{\beta _1Z^*}{(1+\gamma _1P^*)^2}-\frac{\rho Z^*}{(1+\gamma _2P^*)^2}\Big ]\Big \}^{-1}. \end{array} \end{aligned}$$

Using the same notations as in [22], it can obtain

$$\begin{aligned} g_{20}\!&= \!2D\Big \{v_1-1-v_3q_2+\bar{q}_2^*e^{-(\delta +2i\omega ^0)\tau ^0}\Big [(\beta _1 v_3-v_4)q_2-\beta _1 v_1+v_2\Big ]\Big \},\\ g_{11}\!&= \!D\Big \{2( v_1\!-\!1)\!-\! v_3(q_2 \!+\! \bar{q}_2)\!+\!\bar{q}_2^*e^{-\delta \tau ^0}\Big [(\beta _1v_3\!-\!v_4)(q_2\!+\!\bar{q}_2)\!-\!2(v_1\!-\!v_2)\Big ]\Big \},\\ g_{02}\!&= \!2D\Big \{ v_1-1- v_3\bar{q}_2+\bar{q}_2^*e^{-(\delta -2i\omega ^0)\tau ^0}\Big [(\beta _1 v_3-v_4)\bar{q}_2-\beta _1 v_1+v_2\Big ]\Big \},\\ g_{21}\!&= \!2D\Big \{( v_1\!-\!1)\Big [2W_{11}^{(1)}(0)\!+\!W_{20}^{(1)}(0)\Big ]- v_3\Big [W_{11}^{(2)}(0)\!+\!\frac{1}{2}W_{20}^{(2)}(0) +\frac{1}{2}W_{20}^{(1)}(0)\bar{q}_2\\&+W_{11}^{(1)}(0)q_2\Big ]\!-\!3 v_5\!+\!\beta v_7(\bar{q}_2\!+\!2q_2) \!+\!\bar{q}_2^*\Big [e^{-\delta \tau ^0}(\beta _1v_3\!-\!v_4)(e^{-i\omega ^0\tau ^0}W_{11}^{(2)}(-\tau ^0)\\&+\frac{1}{2}e^{i\omega ^0\tau ^0}W_{20}^{(2)}(-\tau ^0) +\frac{1}{2}e^{i\omega ^0\tau ^0}W_{20}^{(1)}(-\tau ^0)\bar{q}_2 +e^{-i\omega ^0\tau ^0}W_{11}^{(1)}(-\tau ^0)q_2)\\&-\,e^{-\delta \tau ^0}(\beta _1v_1-v_2)(2e^{-i\omega ^0\tau ^0}W_{11}^{(1)}(-\tau ^0) +e^{i\omega ^0\tau ^0}W_{20}^{(1)}(-\tau ^0))\\&+\,3e^{-(\delta +i\omega ^0)\tau ^0}(\beta _1v_5-v_6) -e^{-(\delta +i\omega ^0)\tau ^0}(\beta _1v_7-v_8)(\bar{q}_2+2q_2)\Big ]\Big \}, \end{aligned}$$

where

$$\begin{aligned} \begin{array}{c} v_1=\frac{\gamma _1Z^*}{(1+\gamma _1P^*)^3}, v_2=\frac{\rho \gamma _2 Z^*}{(1+\gamma _2P^*)^3},v_3=\frac{1}{2(1+\gamma _1P^*)^2}, v_4=\frac{\rho }{2(1+\gamma _2P^*)^2}, \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{c} v_5=\frac{\gamma _1^2Z^*}{(1+\gamma _1P^*)^4}, v_6=\frac{\rho \gamma _2^2Z^*}{(1+\gamma _2P^*)^4}, v_7=\frac{\gamma _1}{3(1+\gamma _1P^*)^4}, v_8=\frac{\rho \gamma _2}{3(1+\gamma _2P^*)^4}, \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{c} W_{20}(\theta )=\frac{ig_{20}}{\omega ^0}q(0)e^{i\omega ^0\theta } +\frac{i\bar{g}_{20}}{3\omega ^0}\bar{q}(0)e^{-i\omega ^0\theta } +E_1e^{2i\omega ^0\theta }, \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{c} W_{11}(\theta )=\frac{-ig_{11}}{\omega ^0}q(0)e^{i\omega ^0\theta } +\frac{i\bar{g}_{11}}{\omega ^0}\bar{q}(0)e^{-i\omega ^0\theta } +E_2, \end{array} \end{aligned}$$

with

$$\begin{aligned} E_1&= \left( \begin{array}{lc} 2i\omega ^0+P^*-\frac{\gamma _1P^*Z^*}{(1+\gamma _1P^*)^2}&{} \frac{ P^*}{1+\gamma P^*}\\ \;\\ -\Big [\frac{\beta _1Z^*}{(1+\gamma _1P^*)^2}-\frac{\rho Z^*}{(1+\gamma _2 P^*)^2}\Big ]e^{-(\delta +2i\omega ^0)\tau ^0} &{}\, 2i\omega ^0+\delta -\delta e^{-(\delta +2i\omega ^0)\tau ^0} \end{array} \right) ^{-1}\\&\quad \times \left( \begin{array}{c} v_1-1-\beta v_3 q_2\\ \;\\ \Big [(\beta _1 v_3-v_4)q_2-\beta _1 v_1+v_2\Big ] e^{-(\delta +2i\omega ^0)\tau ^0} \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} E_2&= \left( \begin{array}{lc} -P^*+\frac{\gamma _1P^*Z^*}{(1+\gamma _1 P^*)^2} &{} -\frac{ P^*}{1+\gamma _1P^*}\\ \;\\ \Big [\frac{\beta _1Z^*}{(1+\gamma _1P^*)^2}-\frac{\rho Z^*}{(1+\gamma _2 P^*)^2}\Big ] e^{-\delta \tau ^0}&{} 0 \end{array} \right) ^{-1}\\&\quad \times \left( \begin{array}{l} 2(1-v_1)+ v_3(q_2+\bar{q}_2)\\ \;\\ e^{-\delta \tau ^0}\Big [2(\beta _1v_1-v_2)-(\beta _1v_3-v_4)(q_2+\bar{q}_2)\Big ] \end{array} \right) . \end{aligned}$$

Then $g_{21}$ can be expressed by the parameters. Based on the above analysis, we can see that each $g_{ij}$ can be determined by the parameters. Thus it can compute the following quantities:

$$\begin{aligned} \begin{array}{ll} C_1(0)= \frac{i}{2\omega ^0}(g_{20}g_{11}-2|g_{11}|^2-\frac{1}{3}|g_{02}|^2) +\frac{g_{21}}{2},\\ \;\\ \mu _2 =-\frac{\text {Re}\{C_1(0)\}}{\text {Re}\lambda '(0)},T_2=-\frac{\text {Im}\{C_1(0)\}+\mu _2\text {Im}\lambda '(0)}{\omega ^0},\\ \;\\ \beta _2=2\text {Re}\{C_1(0)\}. \end{array} \end{aligned}$$

Hence it has the following theorem.

Theorem 6.1

$\mu _2$ determines the directions of the Hopf bifurcation: if $\mu _2>0(<0)$, the Hopf bifurcation is supercritical (subcritical); $\beta _2$ determines the stability of the bifurcation periodic solutions: the bifurcation periodic solutions are orbitally stable (unstable) if $\beta _2<0(>0)$; and $T_2$ determines the period of the bifurcating periodic solutions: the period increase (decrease) if $T_2>0(<0)$.