1 Introduction

Traction is the resistive force generated during an interaction between studded footwear, for instance a football boot, and a penetrable surface, such as artificial turf [1]. Traction is essential for movements on artificial turf involving changes in velocity, such as accelerations, pivoting movements, or cutting motions [2,3,4]. Rotational traction is a key criterion tested to ensure the safety and performance of artificial turf surfaces, published in the Federation Internationale de Football (FIFA) standards for artificial turf [5]. Governing bodies, such as FIFA and World Rugby, measure rotational traction using a rotational traction tester (RTT) [5, 6]. The RTT contains a studded test foot loaded by freely rotating masses (46 kg). A torque wrench measures the peak torque achieved during manual rotation of the test foot. In 2019, FIFA introduced a lightweight rotational traction tester (LRTT) as an alternative method for measuring rotational traction, to improve the ergonomics and portability of testing. The LRTT uses the operator’s bodyweight to apply normal load through the test foot to the surface. Like the RTT, a torque wrench measures the peak torque generated during manual rotation of the test foot [5]. The LRTT is the primary tester used during on-site field testing, due to its improved portability compared to the RTT [7].

The interaction between boot and surface is complex with twenty-five variables from the surface, footwear, and athlete suggested to contribute to the development of traction forces [4, 8]. Variables, such as infill depth, infill net bulk density, fiber density, and normal load, are known to influence the traction forces generated during a rotational traction test [2, 9,10,11,12,13,14]. Variability in testing results originates from two sources, the turf, and the manual operation of the test device. To date, no study has attempted to quantify the individual contributions of the turf and manual operation to the total variability of test measurements. Previously, the RTT has showed poor reliability in peak torque measurements between trained operators [15]. Past studies have used bespoke automated rotational traction test devices [16,17,18,19]. However, only one study, by Twomey et al., has compared the variability in peak torque measurements between manual and automated test devices [19]. The study comprised ten inexperienced operators who measured the peak torque of an artificial turf surface ten times using both manual and automated test devices. Infill depths were measured before each trial, but not reported. The study omitted the magnitude of reduction in variability caused by automation, choosing to subjectively analyze the spread of results using box and whisker plots [19]. The results showed automation of the test device reduced the spread in mean peak torque measurements between operators compared to a manual device, while the variability in a single operator’s 10 trials showed little difference between devices. Notably, the variability of the test devices used during pitch certification testing remains unknown [5]. Likewise, no study has attempted to quantify the individual contributions to variability from the turf system and from the manual operation of test devices. These represent key gaps in knowledge, given each year operators and test devices from commercial test houses undergo an approval process at a “round robin” test event, where rotational traction results are compared at a carefully prepared outdoor venue.

The primary aim of this study was to estimate the contributions from the turf system and from the manual operation of the test devices to variability in peak torque measurements. Analyzing variability may indicate whether turf research institutes, or standards testing by governing bodies, should use automated devices to better understand the surface properties. The secondary aim was to explore the effects of individual operators and measurement devices on the variability of peak torque measurements. With the use of styrene–butadiene rubber (SBR) as a performance infill becoming more tightly controlled, [20] the inclusion of natural infilled, and non-filled artificial turf surfaces ensured the findings from the study remain relevant for future artificial turf systems.

2 Methodology

2.1 Equipment

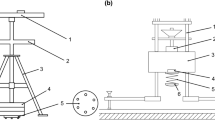
Three different devices measured rotational traction. Two manually operated devices commonly used in pitch certification testing: the RTT and LRTT [5]; and one automated rotational traction tester (ARTT), designed and purpose-built at Loughborough University to enhance artificial turf research (Fig. 1).

Fig. 1
figure 1

Schematic diagrams of the a RTT, b LRTT, and c ARTT

Full size image

Both manually operated test devices complied with the specifications in FIFA’s Quality Programme for Football Turf [5]. The LRTT and RTT are taken as equivalent when measuring rotational traction, however key differences exist between the devices. The RTT test foot is loaded with 46 kg of static mass, giving an overall device mass of approximately 50 kg. The operator stands on the device’s stabilizing frame and rotates a two-handed torque wrench, positioned at a height of 1 m, through at least 45° of rotation at a rate of 72°/s. Conversely, the LRTT is loaded using the operator’s bodyweight, making the device much lighter at approximately 5 kg, improving portability [7]. A spring ensures a load of 450 ± 20 N is applied to the surface through the test foot when the operator stands on the device’s footplate. A single-armed torque wrench, positioned at a height of 0.6 m, is rotated a minimum of 120° at a rate of approximately 30°/s [5].

Additional instrumentation enabled torque and angle of rotation data to be collected throughout each test [8, 9]. For the RTT, a digital torque calibration analyzer (Gedore Torque Ltd, Guildford, The United Kingdom) calibrated a strain gage torque sensor with a resolution of 0.01 Nm and accuracy of ± 0.1 Nm. A Hall effect sensor potentiometer, calibrated to the manufacturer’s specifications, recorded changes in angle, with a resolution of 0.5° and accuracy of ± 1.0°. For the LRTT, a rotary torque/angle sensor (ng-TTR20000-qi, n-gineric gmbh, Villingen-Schwenningen, Germany) measured torque and angle data throughout the rotation; torque with a resolution of 0.01 Nm, accuracy of ± 0.1%, and angle with a resolution of 0.1°, accuracy of ± 0.5°.

The ARTT followed the same test procedure as the RTT [5]; the only difference being an electric motor drove the rotation of the test foot instead of manually rotating a torque wrench. The ARTT is a research tool developed at Loughborough University, for use in the laboratory. At present, the device is not readily portable and unsuited to field testing. Main electricity is required to power the motor, the device has dimensions of 1400 mm × 380 mm × 1000 mm, and a total mass of ~ 60 kg when the standard 46 kg weights are applied. The ARTT’s motor enabled velocities in the range of 0–225°/s and rotational acceleration/decelerations in the range of 0–4000 °/s2. Height adjustable electromagnets suspended the loaded test foot 60 ± 5 mm above the surface before each vertical drop onto the surface. The loaded test foot was then rotated on the surface before being returned to its suspended position. Before the study, a force plate (9287BA, Kistler, Winterthur, Switzerland) confirmed the normal load applied through the test foot as 450.3 ± 19.6 N. A strain gage torque transducer measured the torque throughout a rotation, while a potentiometer measured the angle, comparable to the instrumentation of the RTT. Details of each traction testers design and operating procedure are shown in Table 1.

Table 1 Summary of the test set ups used for the RTT, LRTT and ARTT
Full size table

All three test devices sampled torque and angle data at 250 Hz throughout the rotation. The RTT and ARTT used the same LabVIEW (National Instruments, Austin, USA) program for data collection; the LRTT used n-quirer TT V3.07 software (n-gineric gmbh, Villingen-Schwenningen, Germany).

2.2 Surface systems

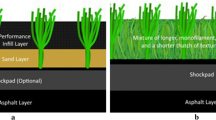
The study included three infilled artificial turf surfaces, and one non-filled surface (Table 2). The wood (BrockFILL), ethylene propylene diene monomer (EPDM), and styrene-butadiene rubber (SBR) infilled surfaces were all 1 m2; the non-filled was a 5 × 1 m section of carpet. All surfaces were constructed to the manufacturer’s specifications and preparation of the surfaces followed the FIFA Quality Programme requirements [5]. The surfaces were prepared and tested at Loughborough University. Once prepared, the infilled surfaces were raked and rolled 50 times with a studded roller. Infill depth was measured at nine locations on the surface using an infill depth gage. The non-filled surface was only raked. Throughout the study, infill depths decreased due to reconditioning, rolling, moving, and testing of the surfaces. Manufacturer’s specifications do not include a tolerance for infill depth; therefore, when a surface’s mean infill depth decreased by 3 mm from the initial mean infill depth (approximately 10% of the infill depth of the lowest filled surface), further infill was added. The reconditioning and infill depth measurements aimed to ensure that each surface remained as close as possible to its original state throughout testing.

Table 2 Summary specifications of each turf system used
Full size table

Pre- and post-study, measurements of rotational traction, shock absorption and vertical deformation were recorded to assess any changes in the surfaces during testing. The ARTT recorded measurements of rotational traction for each surface, while shock absorption and vertical deformation were measured using an Advanced Artificial Athlete (AAA) [5]. The AAA is a mechanical test device which mimics the vertical loading of a human foot strike by dropping a convex test foot onto the surface [21]. Testing with the AAA followed the procedure detailed in the FIFA standards [5]. Shock absorption was calculated using Eq. (1).

$${\text{Shock}}\;{\text{ Absorption}} = \left( {1 - \frac{{F_{\max } }}{{F_{{{\text{ref}}}} }}} \right) \times 100$$
(1)

where Fmax is the peak force during impact, given by Eq. (2), and Fref is a reference force fixed to 6760 N, representing the theoretical force calculated for an impact onto a concrete floor [5].

$$F_{\max } \; = \; m \times a_{\max } - m \times g$$
(2)

where m is the combined mass of the AAA’s falling mass, spring, test foot and accelerometer, g is acceleration due to gravity (− 9.81 m/s2) and amax is the peak deceleration during impact, expressed in m/s2.

2.3 Participants

Five male operators (mean age: 24 years, range: 20–29 years; mean height: 180.0 cm, range: 171.5–190.0 cm; mean body mass: 80 kg, range: 70–90 kg) volunteered to participate in the study. Selection criterion for participation was experience in testing with the RTT, where “experience” was defined as having completed at least 100 supervised laboratory trials with the device.

Only one operator had experience with the LRTT. Therefore, the remaining four operators received training with this device prior to data capture. Clearance from the local ethics committee was gained prior to the study commencing (Review Reference: 2022-8063-9507).

2.4 Data collection

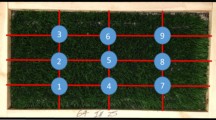
One of each traction tester was used during the study, with each allocated a half-day session per operator. For the RTT, each operator practiced with the device for 10 min prior to testing commencing, focusing on technique, and achieving the desired target velocity. Each operator recorded five trials on a surface before moving to the next. After five trials, each surface was reconditioned (re-raked, rolled 50 times with a studded roller) and nine infill depth measurements were taken, ensuring consistency throughout testing. The same researcher was responsible for all reconditioning and infill depth measurements during the study. This process was repeated until 15 trials had been completed on each of the four surfaces. Individual trials were located consistently on each surface throughout testing; one trial in the center of the surface, and one near each corner. The study followed FIFA’s procedure for laboratory testing, ensuring that the outside edge of the test foot position was 100 mm from a previous test foot location, and 100 mm from the edge of the turf surface [5]. For each half-day session, an online calculator randomized the order of surfaces tested [22].

For the LRTT, the experienced user trained each operator before testing commenced. In brief, the instructions were to load the footplate to ensure full stud penetration into the surface, position their body weight over the test foot to provide the required load, and to rotate the torque wrench 120° over 4 s. The experienced operator analyzed trainee technique during a twenty-minute period on a separate, non-filled artificial turf sample; operators then measured the peak torque twenty times on this sample. The operators were deemed trained if their mean peak torque values were within 5% (approximately ± 1.5 Nm) of that achieved by the experienced tester. Thereafter, the 15 trials on each test surface followed the same procedure as for the RTT.

The ARTT has no operator influence due to its automated rotation, and therefore, only one trained operator used the device. The ARTT recorded two sets of 15 trials to match the FIFA specified rotational velocities for the RTT and LRTT (72 and 30°/s respectively) [5]. Recording at the target velocities of each FIFA device allowed a direct comparison between automated and manual device mean peak torques and negates any velocity influence. Testing with the ARTT used the same trial locations, reconditioning process and surface randomization as previously described for the RTT.

2.5 Data processing

Data from all three devices was stored as.csv files and input into a custom MATLAB (R2021b, The MathWorks, Natick, NJ) script. A 2nd-order, low-pass Butterworth filter (20 Hz) processed the raw data from each trial. A value of 20 Hz was selected using a power spectrum analysis. The power spectrum was visually analyzed to identify the filter frequency which retained the dominant frequencies present in the signal but cut off the frequencies higher than these. A Butterworth filter was selected to preserve the key features of the signal, such as peak torque, while removing high frequency noise. The key outputs of peak torque and angle of peak torque were determined for each trial. Mean speed to peak torque was calculated by numerical differentiation of the angle data with respect to time. The script collated the outputs for each operator into a single excel document.

2.6 Statistical analysis

All statistical analyses were conducted in Microsoft Excel. To evaluate how the surface systems changed during the study, the pre- and post-study mean peak torque, shock absorption, and vertical deformation values for each system were compared using a paired t-test. To assess the consistency of each surface, across each participant’s set of 15 trials (3 sets of 5 trials with reconditioning between each set), a single-factor ANOVA was performed to compare the peak torque values between each set of five trials.

To determine whether differences exist between the peak torque measurements of the RTT, LRTT and ARTT, two different t-tests were conducted. To compare the LRTT and RTT, a paired t-test analyzed differences in the peak torque measurements for every trial completed by the five operators. Due to the difference in sample number between the manual and automated test devices (75 samples for manual test devices, 15 for the automated test device), a Welch’s t-test [23] was conducted to analyze whether differences exist between the RTT and ARTT, and LRTT and ARTT. The rotational velocities of both datasets were matched for this analysis.

Agreement between test devices was further analyzed using Bland–Altman limits of agreement, based on the mean peak torque for each operator, surface and device [24]. The statistical significance of the systematic bias found between devices was analyzed using paired t-tests. Devices producing the same mean peak torque values would generate differences in peak torque measurements of 0 Nm. Therefore, significance was assessed by comparing the calculated statistical bias between the test devices and 0 Nm. Effect size was calculated using pooled standard deviations, due to the datasets having unequal variance, shown in Eq. (3) [25]. For all statistical analyses, alpha level of significance was set at 0.05.

$$d = \frac{{\overline{x}_{1} + \overline{x}_{2} }}{{\sqrt {\frac{{\sigma_{1}^{2} + \sigma_{2}^{2} }}{2}} }}$$
(3)

where d = Cohen’s effect size, \(\overline{x}_{1} \; {\text{and}}\; \overline{x}_{2}\) are the mean of their respective samples, and \(\sigma_{1}\) and \(\sigma_{2}\) are the standard deviations of each respective sample.

Within- or (intra-)operator coefficient of variation (CoVOPERATOR) for the 15 trials of given operator, surface, and device was determined using Eq. (4). The overall within-operator coefficient of variation for each test device (CoVWITHIN) was calculated as the mean CoVOPERATOR across the five operators, given by Eq. (5). The ARTT within-operator CoV was calculated over 15 trials according to Eq. (4).

$${\text{CoV}}_{{\text{OPERATOR }}} = \frac{{{\text{ SD}}_{{\text{ 15TRIALS}}} }}{{\text{Mean Peak Torque }}} \times 100 \%$$
(4)
$${\text{CoV}}_{{{\text{WITHIN}}}} { = }\frac{{{\text{CoV}}_{{\text{OPERATOR 1}}} {\text{ + CoV}}_{{\text{OPERATOR 2}}} {\text{ + CoV}}_{{\text{OPERATOR 3}}} {\text{ + CoV}}_{{\text{OPERATOR 4}}} {\text{ + CoV}}_{{\text{OPERATOR 5}}} }}{{5 }}$$
(5)

Between- or (inter-)operator coefficient of variation (CoVBETWEEN) for each manual test device was calculated as the CoV of the five operator’s mean peak torque measurements for a given device and surface, given by Eq. (6). As only one operator recorded data with the ARTT, an investigation of between-operator variability for the automated test device was not possible.

$${\text{CoV}}_{{{\text{BETWEEN}}}} { = }\frac{{{\text{ SD}}_{{\text{ OPERATOR MEAN PEAK TORQUES}}} }}{{{\text{Overall }}\;{\text{Mean }}\;{\text{Peak }}\;{\text{Torque }}}} \times {\text{ 100 \% }}$$
(6)

By combining the data sets for each testing device, it was possible to estimate the individual contributions of the turf and manual operation to the total variability obtained during testing. Each operator completed 15 trials on a surface, from which the standard deviation in peak torque was calculated (SD15TRIALS). The mean of the five operators SD15TRIALS was calculated as the total variability during rotational testing (SDMANUAL). Automation removes the variability from manual operation. Therefore, the standard deviation of the automated device’s 15 trials comprised variability from the turf only (SDAUTOMATED). By combining these two values, the contributions of the turf and manual operation to total variability were calculated using Eqs. (7) and (8). This process was repeated for both manually operated test devices.

$${\text{\% Manual }}\;{\text{Operation}}\;{\text{ Variability = }}\frac{{{\text{SD}}_{{{\text{MANUAL}}}} - {\text{ SD}}_{{{\text{AUTOMATED}}}} }}{{{\text{SD}}_{{{\text{MANUAL}}}} }} \times 100 \%$$
(7)
$$\% {\text{Turf }}\;{\text{Variability }}\;{ = }\;\frac{{{\text{ SD}}_{{{\text{AUTOMATED}}}} }}{{{\text{SD}}_{{{\text{MANUAL}}}} }} \times {\text{100\% }}$$
(8)

The relationship between the mean peak torque of each surface, measured using the two manually operated devices, and operator anthropometrics was assessed using Pearson’s Correlation Coefficients. Level of significance was again set at the 0.05.

3 Results

For each of the three infilled surfaces, mean infill depths remained consistent throughout testing (Fig. 2). The SBR surface required two top-ups (when mean infill depth had decreased by more than 3 mm from the initial mean infill depth) to maintain infill depth whereas EPDM and BrockFILL surfaces required only one each.

Fig. 2
figure 2

Mean (± standard deviation) infill depths for each of the infilled surfaces, recorded after each surface reconditioning which followed five trials on the surface

Full size image

The key outputs for each surface are shown in Tables 3, 4. Pre- and post-study measurements of peak torque, shock absorption, and vertical deformation are shown in Table 3. While raking and rolling aimed to ensure consistency of the surfaces during testing, it is apparent that the surfaces changed over time. The peak torque increased on all surfaces except the SBR. The BrockFILL and non-filled surfaces were more compliant post-testing. However, the SBR and EPDM surfaces were stiffer, shown by the changes in shock absorption and vertical deformation. These results generally support the overall changes in infill depth. The peak torque, angle of peak torque, and velocity to peak torque measurement for all devices, on all four surfaces are shown in Table 4. All three devices recorded consistent measures for peak torque. The angle of peak torque tended to be slightly lower on the non-filled surface (31°–34°) compared to the infilled surfaces (36°–40°). As expected, rotational velocities for the ARTT matched the FIFA specifications; for both manual devices, the rotational velocities fell below the specification, more so for the RTT compared to the LRTT.

Table 3 Mean (± standard deviation) peak torque, shock absorption and vertical deformation measured pre- and post-study
Full size table
Table 4 Mean (± standard deviation) peak torque, angle of peak torque and velocity to peak torque measured for each surface, test device and operator.
Full size table

The relationships between peak torque measurements from the three traction testers are shown in Fig. 3. The ARTT and RTT produced a small negative systematic bias (− 0.6 Nm, p = 0.23, d = − 0.40), whereas a small positive bias was found between the ARTT and LRTT (0.5 Nm, p = 0.52, d = 0.21). The RTT and LRTT produced a larger, significant systematic bias (2.2 Nm, p = 0.002, d = 1.21). The random bias from the ARTT and LRTT was greater than that for the RTT and RTT, shown by the wider limits of agreement in Fig. 3b (7.1 Nm, − 6.1 Nm, versus 3.7 Nm, − 4.9 Nm). However, this result appears to be due to the changing systematic bias with peak torque for the ARTT and LRTT. On higher peak torque surfaces (BrockFILL), the LRTT under-read the ARTT for all operators, whereas on lower peak torque surfaces (Non-Filled), the LRTT overread the ARTT. No surface torque effects on the systematic bias were visible when comparing the RTT and ARTT, or the RTT and LRTT.

Fig. 3
figure 3

Bland–Altman plots for a ARTT vs RTT; b ARTT vs LRTT; c RTT vs LRTT. The solid black line and adjacent value indicates the systematic bias, and the dashed black lines and adjacent values indicate the 95% limits of agreement

Full size image

Within-operator variability for each device is shown in Fig. 4. Reduced variability in peak torque measurements was found when using the ARTT compared to either manual device. The mean within-operator coefficient of variation when using the ARTT was similar across speeds (4.9% at 72°/s; 5.5% at 30°/s). When comparing manual devices, the LRTT produced lower or equal within-operator variability on all four surfaces compared to the RTT; the LRTT within-operator average variability was 6.1%, compared to 6.8% for the RTT.

Fig. 4
figure 4

Within-operator coefficient of variation for the a RTT (mean ± SD of five operators) and ARTT (72 /s) and b LRTT (mean ± SD of five operators) and ARTT (30°/s)

Full size image

The contribution of the turf system and the manual operation of test devices to the total variability during rotational traction testing were estimated using the within-operator variability (Fig. 5). For both devices, the turf contributed more to the total variability than the manual operation of the device. Manual operation of the RTT, on average, contributed to 28.3% of the total variability (Fig. 5a), whereas manual operation of the LRTT contributed only 11.3% (Fig. 5b).

Fig. 5
figure 5

The estimated contribution to variability from the manual operation and from the turf system for the a RTT and b LRTT

Full size image

The between-operator variability for the RTT and LRTT is shown in Fig. 6. The RTT was less variable between operators compared to the LRTT, with a mean CoVBETWEEN of 3.9% compared to 5.2% for the LRTT. The RTT recorded lower between-operator variability on the three infilled surfaces.

Fig. 6
figure 6

Between-operator coefficient of variation for the RTT and LRTT

Full size image

The effect of operator body mass and height on overall peak torque (averaged over all four surfaces) for both manually operated devices is shown in Fig. 7. Only operator height versus peak torque recorded using the LRTT showed a significant correlation (r = − 0.93, p = 0.02), with taller operators recording lower peak torques on average.

Fig. 7
figure 7

Overall peak torque (averaged over all four surfaces) for each operator plotted against a operator height using the RTT, b operator height using the LRTT, c operator body mass using the RTT, d operator body mass using the LRTT

Full size image

4 Discussion

The results showed the turf consistently contributed over 50% of the total variability during testing for both manual devices, indicating the artificial turf system is the primary contributor to variability during rotational traction testing, not the manual operation of the test devices. Automating the rotation of the test foot reduced the variability in peak torque measurements by providing more consistent and controlled rotations in comparison to the RTT and LRTT. The mean reduction in peak torque variability generated by the ARTT was 28.3% when compared to the RTT, and only 11.3% in comparison to the LRTT; inconsistencies in the turf contribute the remaining variability.

The study suggests that differences in variability exist between the two manually operated devices. The lower within-operator coefficient of variation for the LRTT represents greater repeatability for a single operator’s 15 peak torque measurements. The increased between-operator coefficient of variation for the LRTT indicates that multiple operators report a wider spread of mean peak torque measurements compared to the RTT. Operators’ influence on peak torque measurement was also analyzed; for the LRTT, a significant, strong negative correlation (r = − 0.93, p = 0.02) was found between-operator height and mean peak torque measurements across all surfaces, with taller operators recording lower peak torque values. No correlation was found between mean peak torque and operator height using the RTT, or for operator body mass for either device.

Twomey et al. [19] observed little difference in within-operator variability when comparing an automated and a manual test device. The study implied that for both devices, the variability in peak torque measurements occurs predominantly due to inconsistencies in the turf, agreeing with the results of this study. The current study extends the findings of Twomey et al. [19] using four different turf systems and two different manually rotated test devices. Furthermore, this study has quantified the between-operator variability for the RTT and LRTT, and within-operator variability of all the devices used; enabling the contribution of the turf system, and the manual operation of test devices, to the total variability in peak torque measurements to be estimated. This detailed investigation and analysis into traction measurement variability is the first in literature and highlights important considerations for commercial testing and research. The results show the need to carefully construct and maintain surface systems throughout a study to minimize the variability during testing. Furthermore, there is a need to report the artificial turf system design, maintenance, and reconditioning procedures in published literature to demonstrate rigor and provide comparability for related studies.

The primary contributor to variability in peak torque measurements was the turf system, thought to be caused by inconsistencies around individual studs, and in the contact between the test foot and surface. Mean infill depths were recorded using an infill depth gage and remained consistent throughout testing; however, localized infill depths varied across the surface. Furthermore, as fibers spread randomly from their tufted origin in the carpet backing, localized differences in fiber density are created throughout the surface which can affect infill mobility [14]. Fiber density, infill depth, and infill bulk density all affect the traction recorded on a surface [2, 12,13,14]. Therefore, it is logical to assume that the variability in peak torque across the surface is a result of differences in these variables. The individual mechanisms generating traction require further, detailed research to help understand how the turf and test device interact to affect the traction measured on a surface [3].

Both manual devices are subject to operator-related variability, due to inconsistencies during rotation. Normal load influences traction on artificial turf surfaces, with increased loading causing increases in peak torque [2, 4, 10, 11, 17, 18]. Inconsistent loading may be a problem for the LRTT, due to loading through the operator’s body mass. Incorrect body positioning moves the operator’s center of mass away from the test foot, generating non-uniform load distributions through the test foot. Thus, the load applied to the surface can vary between operators depending on their body positioning. The RTT does not experience such effects as static masses ensure a constant, vertical load throughout the rotation. The differences in loading are likely responsible for the increased between-operator variability found for the LRTT.

Minimal systematic bias was found between the LRTT and ARTT (on average, the LRTT mean peak torque was 0.5 Nm lower than the ARTT mean peak torque (1.2%)); however, this appeared dependent on the surface being tested (Fig. 3b). On the BrockFILL surface, which had the highest mean peak torque values, the LRTT recorded mean peak torque values 4.5 Nm lower than the ARTT. On the non-filled surface, which had the lowest mean peak torque values, the LRTT recorded mean peak torque values 2.6 Nm higher than the ARTT. For the two polymeric infilled surfaces EPDM and SBR, the mean difference in peak torque between the LRTT and ARTT was 0.0 Nm and 0.1 Nm, respectively. The reason for the changing systematic bias is unclear and requires further exploration; anecdotally, the lead author noted that operators struggled to maintain their initial body position while completing trials on the high torque BrockFILL surface. The systematic bias between the ARTT and LRTT, and between the LRTT and RTT, was not dependent on the surface being tested (Fig. 3a and c). The LRTT recorded mean peak torque values 2.2 Nm lower than the RTT (Fig. 3c). A potential reason for this is the difference in target rotational velocity between the manually operated devices. It is currently unknown how rate of rotation affects peak torque measurements [26]. Given polymeric infill materials such as SBR are strain rate-dependent [27], it is plausible that this systematic difference is caused by the difference in target rotational velocity (30°/s for the LRTT and 72°/s for the RTT); however, this also requires further research.

The within-operator coefficient of variation was lower for the LRTT. The lower within-operator variability is potentially a result of the LRTT’s ease of use compared to the RTT. The operators achieved rotational velocities closer to the targets specified in the FIFA Handbook [5] when operating the LRTT compared to the RTT (Table 4). Furthermore, the range of rotational velocities was smaller for the LRTT, shown by the smaller standard deviation values compared to the RTT. This indicates that operators were able to produce more consistent rotations with the LRTT, which may have contributed to the reduced within-operator variability.

Taller operators generated lower peak torque values using the LRTT. The reason for this is unclear; one hypothesis relates again to operator body positioning. The torque wrench for the LRTT is located 0.6 m above the surface (Fig. 1a). Taller operators may struggle to position their center of mass over the test foot as they need to manipulate their body position more to reach and rotate the LRTT’s torque wrench. This potentially leads to non-normal or lower loading through the test foot, causing lower peak torque values [10, 11]. The relationship between-operator height and peak torque found in this study is only valid for the range of operators investigated. Access to experienced operators was limited in this study. Ideally, the study would have accommodated a greater range of operator heights, body masses, and genders to better represent the population of testers in industry; however, operator availability meant this was not possible. While peak torque measured using the LRTT and operator height showed correlation, other anthropometric data was not measured during this study. Measurements, such as torso, arm, and leg length, may also influence peak torque; hence, there is a need to further investigate the relationship between peak torque values measured using the LRTT, torque wrench height and operator anthropometrics.

The findings from this study, combined with previous research, demonstrate that the surface is the primary contributor to the variability in peak torque measurements during rotational traction testing. Despite the automation of testing reducing the variability in peak torque measurements, the evidence suggests that manual operation is not the main cause of variability during rotational traction testing. While automated testing enhances research capabilities and improves data reliability, from this work, it is not considered necessary for commercial laboratory and field testing. Future studies utilizing the ARTT should aim to better understand traction mechanisms [3], and the influence of the variables at the boot-surface interface on the traction forces produced.

Also apparent from this study is the need to better understand the test devices specified in the FIFA Handbook of Test Methods [5]; particularly the LRTT. The LRTT is predominantly used during field testing, due to its increased portability. The increased between-operator variability means surfaces falling close to the upper or lower limit of traction are more dependent on the operator conducting the testing to gain certification. Conversely, the RTT is primarily used during laboratory testing. FIFA specifies that laboratory testing should consist of five trials on a surface; however, the increased within-operator variability of the RTT may indicate a need to increase the number of trials to obtain a better estimate of the true peak torque for that surface.

Key assumptions were made in the results of this study; the first being that the surface variability remained consistent throughout testing. Recording infill depth measurements, reconditioning, and topping up of performance infill levels throughout study aimed to ensure the surface properties remained consistent. Testing the surfaces in a randomized order aimed to remove biases. Furthermore, the surfaces were tested pre- and post-study to assess how much they had changed over the duration of data collection. The results of this study emphasize the need for future researchers to publish the methodologies used to maintain consistent surface properties throughout a study. The second assumption was that the variability in automated testing was entirely from the surface. A small portion of the variability may have originated from the operation of the ARTT. Prior to the study commencing, the authors calibrated the ARTT’s torque measurements, normal load, and rotational accelerations and velocities; the error in these measurements has been reported.

A further observation was that the diameter of the ARTT’s test foot was 2 mm larger (150 mm) than that for both the LRTT and RTT (both 148 mm). All three devices complied with the FIFA Handbook of Test Methods, which states the test foot diameter must be 150 ± 2 mm [5]. A larger test foot applies a lower normal stress to the surface for a given load, due to the greater surface area. For a normal load of 450 N, the decrease in normal stress due to the ARTT’s test foot is 0.7 kPa or 2.7%. While no literature could be found to accurately determine the effect of such a decrease in normal stress, published studies have investigated the effect of normal load on peak torque. Severn et al., found that an increase in normal load from 443 to 543 N (a 22.5% increase) equated to an increase in peak torque of approximately 5 Nm [2]. The percentage difference in normal stress in this study was almost 10 times smaller than that used by Severn et al., suggesting that the effect of the ARTT’s larger test foot on the peak torques generated is likely to have been small.

5 Conclusions

The automation of rotational traction testing reduced variability in peak torque measurements compared to manually operated devices. However, over 50% of the total variability in peak torque for both manually operated devices emanated from the turf. Variability from the turf is considered to originate from localized inconsistencies under the test foot and surrounding the studs, influencing the traction mechanisms. Peak torque measurements with the lightweight rotational traction tester (LRTT) were found to be less variable for a single operator, but more variable between operators compared to the conventional traction tester (RTT).