1 Introduction

One of the main goals for the theory of skiing is to describe the dynamics of skiing turns. The generic ski turn on compacted snow is hybrid in nature. It starts as side-slipping (skidding), where the turning force is likely to originate from the machining (or cutting) of snow, and finishes with carving where the turning force is a component of the normal reaction force originated at the curved platform carved in the snow by the ski. (At the two extremes of this generic turn, we find a purely skidded turn and a purely carved turn, which is initiated by rolling skis from one edge to another.) Hence, understanding of snow machining is an important part of the skiing science.

Lieu and Mote [1] carried out an experimental study into orthogonal machining of ice at rake angles relevant to skiing (negative rake angles). Later they arrived with empirical expressions for the ice-reaction forces as functions of the rake angle and ice penetration (cutting) depth, and used a scaled version of these functions to model ski-snow interaction in skiing turns [2]. A similar study of ice machining, including the oblique case, was carried out by Tada and Hirano [3]. Their findings agreed with [1]. Tada and Hirano [4] and Tada and Kobayashi [5] carried out an experimental study of both orthogonal and oblique machining of compacted snow. In the orthogonal case the relative velocity is orthogonal to the ski longitudinal axis, whereas in the oblique case the angle between the two, the angle of attack, is below \(90^\circ\). Their results could not be fitted by the empirical functions derived in [2], especially at small edge angles (\(< 30^\circ\) ), so they came up with their own empirical functions for the snow reaction forces and used them to model skidded skiing turns.

Brown [6] proposed that snow cutting can be described by the theory of metal machining developed in [7] for the case of continuous (type 2) chip. However, snow and ice are highly brittle materials, and instead of continuous chip their machining normally results in a spray of ice particles. Moreover, in contrast to the large friction between tool and chip in metal machining, the friction between snow and ski is quite low.

In this paper, we describe an attempt to capitalise on the special properties of ice and snow and build a simple approximate model for their machining. Our main hypothesis is that we may neglect the friction between the ski and the spray of ice particles without great loss of accuracy. We check this model against the data of previous laboratory studies and find the results satisfactory. Model that could be easily incorporated into the theory of skiing turns.

2 Materials and methods

In machining of metal, a tool with flat rake face and straight sharp edge moves over a fixed workpiece with its edge lowered down to a fixed cutting depth D. It separates from the workpiece its upper layer as a chip, and this chip works as a link between the uncut metal and the tool (see Fig. 1). The angle \(\varPsi\) between the rake face and the workpiece surface on the chip side can be both above and below \(90^\circ\). The complementary angle \(\alpha _{\text{ r }}=\varPsi - 90^\circ\) is traditionally called the rake angle. In application to skiing, only the case with negative rake angle is relevant, and here we consider only this case. Based on the angle \(\gamma\) between the tool velocity and its edge, one can distinguish the case of orthogonal machining, where \(\gamma =90^\circ\) and the case of oblique machining, where \(\gamma <90^\circ\). In skiing, \(\gamma\) is known as the angle of attack and \(\varPsi\) as the edge angle.

A typical experimental study in industrial machining reduces to determining the forces experienced by the tool as functions of the cutting depth, tool speed, rake angle, angle of attack and other parameters of the tool and the workpiece.

Fig. 1
figure 1

Left panel: interaction of a ski with hard compacted snow as orthogonal machining at negative rake angle \(\alpha =\varPsi -90^\circ\). The sketch shows a cross section of the ski as it skids sideways from right to left. Right panel: Separation of the total reaction force \({\varvec{F}}_{\text{ r }}\) into mutually orthogonal pairs \(\{{\varvec{F}}_{\text{ n }},{\varvec{F}}_{\text{ f }}\}\) and \(\{{\varvec{F}}_{\text{ c }},{\varvec{N}}\}\) in the theory of orthogonal machining [8], where the edge force \({\varvec{F}}_{\text{ e }}\) is not included

Full size image

2.1 Orthogonal machining

The total reaction force \({\varvec{F}}_{\text{ r }}\) applied to the tool by the chip and the workpiece has three main contributors:

$$\begin{aligned} {\varvec{F}}_{\text{ r }}={\varvec{F}}_{\text{ n }}+{\varvec{F}}_{\text{ f }}+{\varvec{F}}_{\text{ e }} \,, \end{aligned}$$
(1)

where \({\varvec{F}}_{\text{ n }}\) is the normal force applied to the tool by the chip at the rake face, \({\varvec{F}}_{\text{ f }}\) is the friction force force emerging at this face (see Fig. 1), and \({\varvec{F}}_{\text{ e }}\) is the force emerging at the edge of the tool [9,10,11]. The edge force is also referred to as a “ploughing”, “parasitic”, and “zero-feed force”, as it remains finite in the limit of vanishing chip thickness. This force emerges because the cutting edge of a real tool is never a perfectly sharp corner but more like a rounded transition zone between the tool faces. Like the force emerging at the rake face, the edge force can be separated into the normal reaction and friction components. However, the local direction of these components varies along the edge surface, and hence the total edge force depends both on the actual size and shape of the edge. The edge can interact both with the chip and with the workpiece material passing under the edge (see Fig. 2). Provided the edge shape is sufficiently close to a cylinder, it can described by just one parameter, the edge radius \(R_\mathrm{{e}}\). The experimental studies show that edge force is substantial only when the cutting depth is small, \(D\lesssim R_\mathrm{{e}}\) [e.g., 10]. In reality, the edge shape can be more complex, and its microscopic scale makes it difficult to measure and control.

Fig. 2
figure 2

Origin of the edge force. \(F_\mathrm{{n}}\) and \(F_\mathrm{{f}}\) are the normal and frictional components of the interaction with the chip at the flat rake face of the tool (e.g. ski base) respectively. \({\varvec{F}}_{\text{ e,n }}\) and \({\varvec{F}}_{\text{ e,f }}\) are the corresponding local components of the interaction at the rounded edge of the tool. The dashed lines show the flow of the workpiece material (e.g. snow) in the rest frame of the tool

Full size image

Geometrically, the resultant force can be split into the component normal to the uncut workpiece surface, \({\varvec{N}}\), known as the “feed” or “thrust” force, and the component aligned with this surface, \({\varvec{F}}_{\text{ c }}\), known as the “cutting force”. In skiing, \({\varvec{N}}\) mostly balances the component of Earth’s gravity that pushes the skier against the ski slope. Hence, at first approximation, \({\varvec{N}}\) can be considered as fixed. The cutting component resists to skier’s skidding and depends not only on their state of motion but also on the condition of their skis. For example, in machining of metals, the cutting force may increase rapidly with the reduction of \(R_e\), as can be seen in Fig. 5 in [10]. The same is likely to be true for machining of snow and ice. The importance of keeping ski edges sharp is well known to ski racers, who regularly ski on hard icy show that allows only shallow penetration by the ski edge. It is natural to assume that sharping ski edges allows to reduce the parasitic edge force.

If the edge force is negligibly small, then from the basic geometry of the problem (see Fig. 1), it follows that in orthogonal machining:

$$\begin{aligned} F_{\text{ c }} = N \tan (\varPsi -\tau )\,, \end{aligned}$$
(2)

where \(\tau =\arctan \mu\) is called the friction angle and \(\mu\) is the kinetic coefficient of friction [8]. This result should be compared to the Coulomb law of friction:

$$\begin{aligned} F_{\text{ Cf }} = \mu N \,. \end{aligned}$$
(3)

While in both cases, the forces are proportional to N and do not depend on speed, the cutting force is determined largely by the edge angle and its dependence on the coefficient of friction is rather different. In particular, the friction between the chip and the rake face does not oppose the tool motion but supports it instead. This somewhat peculiar property emerges because the chip escapes in the general direction of tool motion (see Fig. 1).

This force vanishes when \(\varPsi = \tau\) and even changes its direction to the opposite when \(\varPsi <\tau\). This implies that the workpiece does no longer resists its machining, which is unrealistic, and suggests that Eq. (2) becomes inapplicable at such small edge angles. Presumably, the chip is no longer formed, the tool just slides over the workpiece, and the cutting force is replaced by Coulomb friction.

In the case of metals, \(\mu\) can be high. For example, for clean and dry steel surfaces \(\mu =0.5-0.8\) [12], leading to the friction angle \(\tau =26-39^\circ\). In contrast, ice and compacted snow are very slippery and characterised by much lower values of \(\mu\) [e.g. 13, 14]. In gliding experiments, the value typical for properly prepared skis is \(\mu \le 0.04\), and the corresponding friction angle is below \(2.3^\circ\). Such a low value of \(\mu\) not only suggests that Eq. (2) is accurate most of the time, but also that it can be replaced with a simpler version:

$$\begin{aligned} F_c = N \tan \varPsi \,, \end{aligned}$$
(4)

where the snow friction is completely ignored.

Ice and compacted snow are extremely brittle and easily disintegrate into individual grains under sufficiently high strain rate, with very low energy consumption compared to other materials [e.g., 15, 16, 4]. As a result, instead of a continuous chip, a spray of pulverised snow is formed. The process of snow/ice crushing is likely to proceed in a quasi-periodic fashion: a snow crushing event is followed by an ejection of pulverised snow, contact of the ski edge with yet untouched snow, and then next crushing event. Due to its fluidity, the friction between the spray and the ski base may be even lower than the friction between the ski base and uncrushed snow.

Another important difference between machining of materials in typical industrial (and laboratory) settings and skiing is in the general problem setup. In industrial setup, the cutting depth is predetermined by the way the tool is fixed in the cutting machine. Hence the depth is considered as free parameter. Both the feed and the cutting forces emerge as responses to the preset cutting depth (and other machining parameters). In skiing, one cannot set the cutting depth at will, obviously. Moreover, the feed force \({\varvec{N}}\) is set by the need to balance the component of the gravity force that pushes the skier against the ski slope. Hence it is largely predetermined by skier’s mass and the gradient of ski slopeFootnote 1. On the other hand, the cutting depth, and hence the cutting force becomes a variable response to the applied pressure (and other machining parameters). Moreover, equations like (2) and (4) allow to completely bypass the cutting depth in determining the cutting force.

Fig. 3
figure 3

Separation of the cutting force \({\varvec{F}}_{\text{ c }}\) into braking \({\varvec{F}}_{\text{ b }}\) and turning \({\varvec{F}}_{\text{ t }}\) components. \(\hat{{\varvec{s}}}\) is the unit vector aligned with the ski, \(\hat{{\varvec{m}}}\) is the unit vector in the direction of motion on the snow, \(\hat{{\varvec{n}}}_{\text{ s }}\) is the unit vector orthogonal to \(\hat{{\varvec{s}}}\) as described by Eq. (7), and \(\gamma\) is the angle of attack

Full size image

2.2 Oblique machining

In oblique machining, the tool edge is no longer orthogonal to the relative velocity between the tool and the workpiece. As a result, the relative velocity of the chip has a component aligned with the edge direction and so does the friction force between the chip and the rake face. This make oblique machining more complex. If however the friction force is negligibly small, this difference is of no importance, and the snow reaction is still dominated by normal reaction force at the rake face (\({\varvec{F}}_{\text{ n }}\)). Hence, for machining of ice and snow we may still write

$$\begin{aligned} {\varvec{F}}_{\text{ r }} = {\varvec{N}}+ {\varvec{F}}_{\text{ c }}, \end{aligned}$$
(5)

and

$$\begin{aligned} {\varvec{F}}_{\text{ c }} = F_{\text{ c }} \hat{{\varvec{n}}}_{\text{ s }}, \end{aligned}$$
(6)

where \(F_c\) is the same as in the case of orthogonal machining (Eq.  4) and \(\hat{{\varvec{n}}}_{\text{ s }}\) is the unit vector in the workpiece plane that is orthogonal to the tool edge and points away from the uncut side of the workpiece. If \(\hat{{\varvec{s}}}\) is the unit vector aligned with the tool edge and \(\hat{{\varvec{m}}}\) is the unit vector in the direction of the relative motion, then

$$\begin{aligned} \hat{{\varvec{n}}}_{\text{ s }} = \frac{({\varvec{\hat{{\varvec{m}}}}} \!\times \! {\varvec{\hat{{\varvec{s}}}}})\times \hat{{\varvec{s}}}}{|{\varvec{\hat{{\varvec{m}}}}} \!\times \! {\varvec{\hat{{\varvec{s}}}}}|} \,. \end{aligned}$$
(7)

Figure 3 shows these vectors in the context of skidding ski. These equations can be derived from the equations of oblique machining as given in [17] in the limit of vanishing friction between the tool and the chip. The effect of motion along the cutting edge was also ignored in [2].

In application to skiing, the component of \({\varvec{F}}_{\text{ c }}\) aligned with the relative velocity is responsible for braking and the component orthogonal to it is responsible for turning. Hence we denote these components as \(F_{\text{ b }}\) and \(F_{\text{ t }}\) respectively (see Fig.  3 ). Obviously

$$\begin{aligned} F_{\text{ b }} = F_{\text{ c }} \sin \gamma \quad \text{ and }\quad F_{\text{ t }} = F_{\text{ c }} \cos \gamma \,. \end{aligned}$$
(8)

Thus, the cutting force contributes mostly to braking at large angles of attack and mostly to turning at small angles of attack. (In the theory of machining, \({\varvec{F}}_{\text{ b }}\) is still called the cutting force and \({\varvec{F}}_{\text{ t }}\) is called the radial force.)

3 Results

3.1 Comparison with laboratory experiments in machining of ice and snow

There have been only a handful of laboratory studies into machining of ice and snow.

Lieu and Mote [1] experimented with orthogonal machining of ice using a flat-faced tool with sharp egde, positioned at negative rake angle. In their experiments, they varied the machining speed from 0.01 to 1 m/s, the cutting depth from 0.04 to 1.2 mm, the edge angle from \(30^\circ\) to \(75^\circ\). The total cutting force per unit edge length could reach 12 kN/m.

The dependence of both the feed and cutting components of the ice reaction force on the cutting depth, found in their experiment, shows a transition from a nonlinear growth at low depths to a linear one at high depths. Such a transition is also typical for machining of metals and occurs at \(D\approx R_e\). Unfortunately, Lieu and Mote [1] do not provide any quantitative measures for the edge sharpness of their tools.

They also found that in all cases the resultant ice reaction force was almost normal to the rake face, in agreement with Eq. (4). At the lower end of the cutting depth range, the chip was more or less continuous, but at the higher end it was in the form of spray of small ice particles. In the latter case, Lieu and Mote [1] observed a pronounced tool chatter and fluctuation of the cutting force at 10% level, as expected for quasi-periodic crushing of ice [15]. Later, Tada and Hirano [3] found a reasonable agreement with the results of [1] in their own experiments in ice machining.

Fig. 4
figure 4

Left panel: function F(x) given by Eq. 9 (dashed line) against \(\tan x\) (solid line). Right panel: the experimental points computed from the data of [4], against \(\tan \varPsi\) (dashed line) and \(1.45\tan \varPsi\) (solid line)

Full size image

Tada and Hirano [4] carried out similar experiments with orthogonal and oblique machining of compacted snow of density 383 kg/m\(^3\), at the cutting speed \(\approx 0.07\) m/s, and the edge angle in the range \(15^\circ \le \varPsi \le 90^\circ\). They found that all components of the snow reaction force were proportional to the cutting depth and used nonlinear regression to obtain empirical expressionsFootnote 2 for the components as functions \(\varPsi\) and \(\gamma\). According to their formulae, in the orthogonal case (\(\gamma =90^\circ\))

$$\begin{aligned} \frac{F_{\text{ c }}}{N} = A F(\varPsi )\,, \quad \text{ where }\quad F(\varPsi ) = \frac{\varPsi ^{3.993} (\tan \varPsi )^{0.0153}}{(\sin \varPsi )^{2.94}} \end{aligned}$$
(9)

where \(A=1.7\times 10^{-7}\). The function \(F(\varPsi )\) is quite close to \(\tan (\varPsi )\) for \(0^\circ < \varPsi \lesssim 70^\circ\) (see the left panel of Fig. 4), suggesting a good agreement with what was found for ice cutting in [1]. However, the value of A is unrealistic and presumably results from a typographical error. We used image manipulation program GIMP, to read the values of N and \(F_c\) from their regression curves (their figure 6), and hence to calculate \(F_c/N\) . The results are presented in the right panel of Fig. 4 and correspond to \(A=1.45\). Thus, the values of the cutting force predicted by Eq. (4) are about 30% lower than the values found in this experiment.Footnote 3 We also note that the dependence of \(F_{\text{ c }}\) on \(\varPsi\) reported in [4] is qualitatively different from that found in ice machining in [1], and later in snow machining in [5]—\(F_{\text{ c }}\) does not monotonically decrease but has a global maximum at \(\varPsi \approx 45^\circ\).

The empirical dependence of the snow reaction force on \(\gamma\) given in [4] is rather different from that given by Eq. (8). Unfortunately, they did not present any plots comparing this dependence with their experimental points, and hence it is impossible to tell how well they agree. It is also impossible to read with confidence the experimental data from the plots that are presented in the paper.

A similar experimental study in machining of snow was made by Tada and Kobayashi [5].Footnote 4 It involved a snow specimen of density \(550\,\) kg/m\(^3\) placed on a rotating table. This approach allowed to reach the cutting speed approaching the typical speed of skiing (2–5 m/s). The snow specimen was machined with cutting tools shaped in such a way that the angle of attack was the same at every position on the cutting edge. The paper does not tabulate the experimental data but presents them in the form of plots, including those showing the dependence of the snow reaction force on the angle of attack. Fortunately, the plots do not have many experimental points, which makes their identification unambiguous. Once again, we used the image manipulation program GIMP to convert the data into digital form and then to calculate the normalised braking and turning forces, \(F_{\text{ b }}/N\) and \(F_{\text{ t }}/N\).

Fig. 5
figure 5

Fitting of the experimental data of [5]. The filled circles are the experimental points for the normalised braking force \(F_{\text{ b }}/N\) and the squares are the experimental points for the normalised turning force \(F_{\text{ t }}/N\). The dashed lines correspond to \(F_{\text{ c }}=\tan \varPsi N\) and the solid lines correspond to \(F_{\text{ c }}=(\tan \varPsi +0.2)N\)

Full size image
Fig. 6
figure 6

Total normalised cutting force \(F_c/N\) in the experiment of [5] as function of the attack angle \(\gamma\). The dash horizontal line shows the value for orthogonal machining

Full size image

In Fig. 5, the experimental data obtained in this way (squares and circles) are compared against the theoretical predictions based on Eqs. (4) and (8) (dashed lines).Footnote 5 One can see that our model agrees quite well with the experimental data for oblique machining at the edge angle \(\varPsi =45^\circ\) (right panel), but gets worse for \(\varPsi =15^\circ\) (middle panel). Visual inspection of the data for orthogonal machining (left panel) suggests that the data points are shifted above the theoretical curve by about 0.2. So next we tried \(F_{\text{ c }}/N = \tan \varPsi + 0.2\). Using this modification we obtained the theoretical curves shown in Fig. 5 as solid lines. One can see a substantial improvement for the \(\varPsi =15^\circ\) case and some improvement for the \(\varPsi =45^\circ\) case as well. This suggests that the main reason for the disagreement is underestimation of the total cutting force. To verify this, we have computed \(F_\mathrm{{c}}/N\) for all the experimental points. The results are shown in Fig. 6. One can see that \(F_\mathrm{{c}}/N\) does not depend on the angle of attack, in agreement with Eq. (8).

3.2 Snow spaying in skiing and ice skating

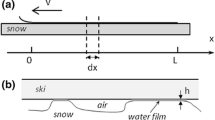
Side-slipping or skidding is a part of many ski turns. Some turns can be fully skidded, others are hybrid and have a skidded section followed by a carved one. At high speed, skidding is accompanied by sprays of snow. A similar phenomenon is observed in ice skating and in water skiing. Whereas water is a fluid and the physical mechanism of spraying can be described entirely by fluid dynamics, the ice and snow are solid, which implies a different mechanism. Following the study of ice-crushing by Jordaan and Timco [15], we propose the following model based on the extreme brittleness of ice and snow. When skis (skate blades) machine snow (ice) they crush small portions of this snow (ice) in its vicinity. In Fig. 7 this volume of crushed (pulverised) snow is represented by the parallelogram aligned with the ski base. Its horizontal width is denoted as W and its length along the ski base as L. After an event of snow crushing, the ski keeps its side-slipping with the mean speed \(V_\perp =V\sin \gamma\) and squeezes the snow powder produced during this event out of the crushed layer. Then the ski hits the wall of undisturbed snow and drives another snow crushing event, and so on. The process continues in a quasi-periodic fashion.

Treating the powder as incompressible fluid, we can estimate the normal to the slope component of the spray velocity \(V_{\text{ sp,n }}=V_{\text{ sp }}\sin \varPsi\) as

$$\begin{aligned} V_{\text{ sp,n }} = \frac{D}{W} V_\perp \,, \end{aligned}$$
(10)

where the cutting depth \(D=L\sin \varPsi\). In principle, this result can be tested in a laboratory experiment, but we are not aware of any such study. Let us use this equation to estimate the expected size of the crushed snow under the conditions typical for skiing.

This can be done based on the height h of the spray trail left by a skier. Once ejected, the ice particles move as projectiles and hence

$$\begin{aligned} h = \frac{V_{\text{ sp,n }}^2}{2 g} \,. \end{aligned}$$
(11)

Combining this result with (10), we obtain

$$\begin{aligned} \frac{D}{W} = \frac{\sqrt{2gh}}{V\sin \gamma } \,. \end{aligned}$$
(12)

Using \(V=15\,\)m/s and \(\gamma =10^\circ\), which are typical for competitive slalom [18], as well as the realistic value \(h=0.5\,\)m (see the image in Fig. 7), we obtain \(W/D=1.2\).

Fig. 7
figure 7

Left panel: squeezing pulverised snow out of the layer with the depth D and width W produced in the latest snow-crushing event. Right panel: the spay fan as seen at the \(90^\circ\) viewing angle to the ski

Full size image

In addition, one can use the observed values of \(\theta _{\text{ sp }}\), the observed opening angle of the spray fan in projection onto the plane defined by the ski and the normal to the slope. Since \(\tan \theta _{\text{ sp }}=V_{\text{ sp,n }}/V_{\parallel }\), where \(V_{\parallel }=V_\perp /\tan \gamma\), we have

$$\begin{aligned} V_{\text{ sp,n }} = V_\perp \frac{\tan \theta _{\text{ sp }}}{\tan \gamma } \,. \end{aligned}$$
(13)

Combining this result with (10), we obtain

$$\begin{aligned} \frac{D}{W} = \frac{\tan \theta _{\text{ sp }}}{\tan \gamma } \,. \end{aligned}$$
(14)

Our naked eye observation of numerous skiing videos suggest that \(\theta _{\text{ sp }}\approx \gamma\) and hence \(W \approx D\).

Thus, the transverse length scale of crushed snow is about the same as the cutting depth. For icy snowpack D cannot be more than several millimetres [19]. Under these conditions, the layers of pulverised snow are narrow and side slipping over a distance of one ski width is accompanied by numerous micro-events of snow crushing. Ice spraying in ice skating, e.g., during a hockey stop, should be of the same origin.

4 Discussion

In orthogonal machining (\(\gamma =90^\circ\)), the relation between \({\varvec{F}}_{\text{ c }}\) and \({\varvec{N}}\) is similar to Coulomb’s law of friction, \(F_c=\mu _{\text{ eff }}N\), with the effective kinetic friction coefficient \(\mu _{\text{ eff }}= \tan \varPsi\). This coefficient can become large for sufficiently high edge angles, e.g., \(\mu _{\text{ eff }}=1\) for \(\varPsi =45^\circ\), which is consistent with the very efficient braking during the so-called “hockey stop” manoeuvre.

For oblique machining, \({\varvec{F}}_{\text{ c }}\) is no longer counter-aligned with the velocity vector and can be split into the braking component \(F_{\text{ b }}=F_{\text{ c }}\sin \gamma\) (counter-aligned with the velocity) and the turning component \(F_{\text{ t }}=F_{\text{ c }}\cos \gamma\) (orthogonal to the velocity). Since the typical value of the attack angle in skiing turns is usually small, \(\lesssim 10\)–\(20^\circ\) [e.g. 18, 20], the braking component is much lower than in hockey stops, and the snow cutting force contributes mainly to turning. However, the braking component is still important, yielding the effective friction coefficient \(\mu _{\text{ eff }} \lesssim 0.18\)–0.36 for \(\varPsi =45^\circ\). This component of the cutting force may explain the abnormally high values of the kinetic friction coefficient obtained in several field studies of alpine skiing [20, 21].

Testing our theory against the data of laboratory experiments with ice and snow shows a good agreement, but also indicates that the theory may under-predict the strength of \({\varvec{F}}_{\text{ c }}\) for snow. It is not clear if the deviation is significant. Indeed, we find that for the data given in [4] the under-prediction increases with the edge angle, whereas for the data in [5] it decreases with the edge angle. Moreover, [4, 5] give qualitatively different results for \(F_{\text{ c }}(\varPsi )\), which we find difficult to explain.

If the under-prediction of cutting force is real, it may be due to the simplifications of the model. The main simplification is the neglect of the friction and edge forces. We think this simplification is unlikely to result in under-prediction. Indeed, incorporation of the friction force between the rake face and the snow chip would not increase but further reduce the cutting force (see the discussion after Eq. 2). The edge force is important only when the cutting depth D is less or comparable to the sharpness radius of the cutting edge \(R_{\text{ e }}\). Unfortunately, the value of \(R_{\text{ e }}\) in these experiments is unknown. The edge force may have been important in the ice experiments [1], as indicated by the non-linear behaviour of N(D) and \(F_{\text{ c }}(D)\) at \(D\lesssim 0.1\,\) mm, but their results agree well with our model anyway. In the snow experiments, the cutting depth was quite large, \(3 \, \text {mm} \le D\le 6 \, \text {mm}\) [4, 5] and hence much higher than \(R_{\text{ e }}\) for any reasonably sharpened tool. Moreover, the snow reaction force was found to be proportional to the cutting depth, which suggests the regime \(D\gg R_e\) where the edge force is relatively small [e.g., 10]. Further experiments are needed to resolve this issue.

The cutting tools used in the past laboratory studies of snow machining are rigid, whereas skis are flexible and skier’s weight (or load) distribution along the ski and hence the distribution of the cutting force are highly nonuniform [e.g., 22]. Finite torsional stiffness of skis means that the edge angle also varies along the ski edge. Finally, alpine skis, particularly the modern shaped skis, bend when put on edge, meaning that the angle of attack varies as well. All these factors are important for top performers, and particularly elite racers, for whom even minute improvements make a difference. However, they still seem secondary and we expect that essentials of many skiing manoeuvres can be captured using rather simple models.

We propose that crushing (or pulverising) of snow is a key component of snow machining in skiing due to the brittle nature of compacted dry snow and ice. This is supported by the observed ejection of snow plumes roughly in the plane of the ski base. Less pronounced, but still noticeable plumes are produced even in clean carving turns. This suggests that trenches made in the snow by a carving ski are also a result of snow crushing, rather than its elastic or plastic deformation [cf. 19, 23].

5 Conclusion

In this paper, we presented an approximate theory of snow machining by a side-slipping (skidding) ski. Ignoring the edge force and the friction between the snow chip and ski base, we derived simple equations relating the cutting component of the snow reaction force with its normal component, the tool edge angle, and the angle of attack \(\gamma\). The theory is consistent with the results of laboratory experiments in machining of ice and snow, but may under-predict the cutting force in the case of snow. New dedicated experiments are required to establish the accuracy of this theory.

In application to skiing, the theory leads to a simple model of skidding, that relates the turning and braking forces to the skier’s weight and the skis edge and attack angles. Our analysis shows that this model is capable of explaining the efficiency of hockey stop, the abnormal “friction” reported in several field studies of alpine skiing, and the parameters of snow plumes accompanying skidding. This model promises to evolve into a relatively simple model of skiing turns involving skidding phase.

The theory needs proper verification via experiments on ski slopes. We have already applied our model to one of the most basic skiing manoeuvres, straight-line traversing across ski slope. This manoeuvre would be impossible if the ski-snow interaction was governed by Coulomb’s friction. However, it is allowed by our model of skidding. The results of this study are being prepared for publication elsewhere.