1 Introduction

Pole vaulting is an astonishing sport where athletes use poles as an auxiliary equipment to clear the bar at heights of 5–6 m and more. Risen from a purpose driven technique, e.g., overcoming castle walls during siege, crossing irrigation ditches [1] and transport [2], pole vaulting has become one of the most spectacular and high-tech disciplines at the Olympic games. It is a dynamic, elegant and fascinating sport.

To clear the bar, pole vaulters need to transfer the kinetic energy of the approach into potential energy via the pole. Two factors determine the success of a vault: (1) physical abilities of the athlete (speed, strength and springiness) and (2) properties of the pole (low weight and ability to store and return energy in the most efficient way).

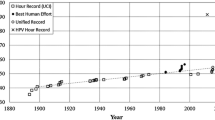
In times where the physical abilities of the athletes reach their limits, the pole and, thus, the material it is made of, becomes a key factor. Figure 1 depicts the development of the world record in pole vaulting over time.

Fig. 1
figure 1

World record in pole vaulting over time with different materials (data from Hirn [3])

Full size image

In the early 20th century, bamboo poles were utilized which are light but also very stiff and, thus, not able to transfer the kinetic energy from the approach in an efficient manner. In the 1940s, aluminum and steel led to new world records—however, these materials show high stiffness as well and therefore did not significantly improve the vaulting height. In the beginning of the 1960s, lightweight fiber-reinforced plastics (with lower bending stiffness) became increasingly popular. They allow large elastic deflections. As a consequence, they are able to transfer more energy resulting in a more pronounced catapult effect. In the following years, the world record steadily rose due to improved fiber arrangements and vaulting techniques. In the 1990s, a new plateau of nearly 6.15 m was reached. This indicates that human physiology and current materials may have reached a limit and enhancements of the pole’s material are necessary to further improve the world record. The aim of this work is to provide a finite element (FE) model allowing for simulation aided pole design.

2 Model specifications

FE simulations of the pole vaulting process were conducted with the commercial FE code abaqus 6.14. The initial boundary value problem of the dynamic equation of motion was solved with an implicit time integration method under consideration of finite deformations. Exemplary FE models of the pole and the vaulter were obtained and generated in abaqus/CAE. To capture the kinematics of the pole vault procedure, a setting was employed that couples pole and vaulter allowing for a relative motion.

2.1 Finite element model of the vaulter

A comprehensive overview of the mechanics of pole vaulting can be found in Frère et al. [4] describing the process in four steps: run-up, take-off, pole bending and pole straightening. A crucial part in the jumping process simulation is the description of the vaulter. Muscle work of the vaulter increases the performance [5, 6]. In addition, the moment exerted on the pole by the vaulter influences the vaulting performance [7]—elite vaulters bend the pole such that its effective lengthFootnote 1 relative to the original length is reduced by ca. 30% [8]. As stated by Ekevad and Lundberg [9], a modeling approach representing the vaulter by a point mass with a fixed position relative to the pole is not sufficient. The complex motion in combination with muscle work needs to be considered.

Hubbard [10] applied a model of the vaulter consisting of three rigid segments representing different parts of the body. Ekevad and Lundberg [11] extended this approach to six segments in a 2D setting, sequentially connected by joints: forearm, upper arm, head, trunk, thigh and shank (cf. Fig. 2).

Fig. 2
figure 2

Model of the vaulter based on Ekevad and Lundberg [11]

Full size image

The two arms and legs were represented by one equivalent segment. A summary of the properties of the segments is shown in Table  1. In this paper, we extend the approach of Ekevad and Lundberg [11] by additionally accounting for a joint at the neck.

Table 1 Properties of segments of vaulter model (data from [11])
Full size table

An exemplary motion of a vaulter was obtained by analyzing videos of a German elite pole vaulterFootnote 2. Specific frames of the video were taken to represent different phases of the vault process. With the aid of CAD software several measurements were taken for each phase to describe the position of the vaulter’s body segments. In accordance with the planar motion of the segments model, a side view was considered in the videosFootnote 3. The motion was described relative to the upper pole tip. Thus, it can be used in simulations with poles of different lengths. To do so, three coordinate systems were introduced as shown in Fig. 2. First, the global coordinate system x–y was fixed and located at the lower tip of the pole. Second, a relative coordinate system \(x_{1}\)–\(y_{1}\) was established at the upper tip of the pole. In addition, a relative coordinate system \(x_{2}\)–\(y_{2}\) was utilized with an origin coinciding with the previous one. This coordinate system rotates to maintain the \(x_{2}\)-axis tangential to the pole. The measured quantities are:

  • Angle \(\varphi\) between ground and a line connecting the tips of the pole,

  • Height \(h_{\mathrm {p}}\) of upper pole tip,

  • Angle \(\theta _{0}\) of the rotated coordinate system \(x_{2}\)–\(y_{2}\),

  • Angle \(\theta _{1}\) between the coordinate system \(x_{2}\)–\(y_{2}\) and segment A, and

  • Angles \(\theta _{2}\) to \(\theta _{6}\) between the segments A to F.

The angles \(\theta _{i}\) between the body segments of the reference pole vault over time are plotted in Fig. 3. A linear interpolation was performed between the discrete values.

Fig. 3
figure 3

Body segment angles in reference pole vault. Those are used as input during the FE simulations

Full size image

At a second stage, the body was reduced to a point mass (center of gravity) with m = 80 kg. Thus, the significant effort to control the individual segments of the vaulter with muscle torques is avoided allowing more computational time on material modeling. The position of the mass center \(\varvec{x}_{m}\) in the coordinate system \(x_{2}\)–\(y_{2}\) was calculated from the measured angles in each phase by

$$\begin{aligned} \varvec{x}_{m}= \begin{bmatrix} x_{m}\\ y_{m}\\ \end{bmatrix} =\frac{\sum _{i=\mathrm {A}}^{\mathrm {F}}\varvec{x}_{i}m_{i}}{\sum _{i=\mathrm {A}}^{\mathrm {F}}m_{i}}, \end{aligned}$$
(1)

where \(\varvec{x}_{i}\) is the position of the mass center of the ith segment of the body and \(m_{i}\) is the mass of the ith segment. The point mass moves relative to the pole in coordinate system \(x_{2}\)–\(y_{2}\) applying abaqus’ connector elements (cf. Sect. 2.3). The different phases of the vault and the position of the mass center (blue square) are illustrated in Fig. 4.

Fig. 4
figure 4

Positions of the vaulter’s body segments and mass center (blue square) during different phases of the pole vault. Coordinate system \(x_{1}\)–\(y_{1}\) is chosen for the presentation (color figure online)

Full size image

We employed two variables during the pole vault to trigger the relative motion of the point mass: the pole angle \(\varphi\) from take-off to the instance of maximum pole bending, and the relative height \(h_{m,\mathrm {rel}}\) of the point mass from maximum pole bending till pole releaseFootnote 4. This is due to motion of the point mass relative to the pole that cannot be implemented as time based. It depends on properties of the pole such as the pole’s length and stiffness—these properties, however, are to be varied during the simulations.

2.2 Finite element model of the pole

Modern, elite vaulting poles are manufactured out of lightweight materials consisting mainly of glass fiber-reinforced plastics. The fiberglass pole is rolled on a mandrel and, subsequently, wrapped to stiffen the pole. The perfect pole differs for athletes, depending on their physical properties, abilities and vaulting technique- and plays an essential role in the vaulter’s performance.

As a first step, an isotropic hyperelastic material model of Neo-Hookean type was applied with the strain–energy function

$$\begin{aligned} \Psi =\frac{\mu }{2}\left[ {I}_{1}(\hat{\varvec{b}})-3\right] +\frac{\kappa }{2}[J-1]^{2}, \end{aligned}$$
(2)

where \(\mu\) is the shear modulus, \({I}_{1}=\mathrm {tr}(\hat{\varvec{b}})\) is the first invariant of \(\hat{\varvec{b}}\), \(\hat{\varvec{b}}=J^{-2/3}\varvec{b}\) is the distortional component of the left Cauchy–Green strain tensor, \(\kappa\) is the bulk modulus and J is the determinant of the deformation gradient \(\varvec{F}\). Neo-Hookean hyperelasticity renders linear elasticity as long as it is valid but also allows for nonlinear behavior which occurs due to the large deflection of the pole. Therefore, it is the more general choice. The material density \(\rho\) and the Poisson’s ratio \(\nu\) were calculated with the rule of mixtures (following [13]) for a fiber volume fraction of 50% as in Davis and Kukureka [14]. The modulus of elasticity was obtained via a flex test simulationFootnote 5. This kind of test is used in the pole industry to classify the stiffness of a pole. The pole is pin-supported at both ends and loaded with a mass of 22.7 kg in the center. The deflection in cm gives the flex number (a relative stiffness number) of the pole. The assumed geometry of the equipment, namely the pole, is shown in Fig. 5. Table 2 summarizes the chosen properties. In the study on the pole stiffness (see Sect. 3), the elastic modulus is varied in the neighborhood of the previously calculated value of the flex test.

We discretized the pole with continuum elements as well as beam elements and compared the outcome. Continuum elements can represent arbitrary structures and bodies and can resolve complex three-dimensional stress states. Further, they allow for incorporating user defined material laws which might be desired when accounting for microstructure, for example. Structural elements such as beams rely on assumptions like slenderness simplifying the model to one predominant dimension. This leads to a reduced number of degrees of freedom and therefore, higher computational efficiency. abaqus’ Timoshenko beam elements capture large axial strains [15].

Fig. 5
figure 5

Dimensions of the pole: a tube like structure of length L featuring a hollow cross-section with radius R and wall thickness t

Full size image
Table 2 Summary of the properties of the pole
Full size table

2.3 Coupling of pole and vaulter

The point mass needs to be connected to the pole such that it can move relatively to the upper pole tip according to the vaulter’s motion in different phases of the vault. Moreover, the connection fails once the pole is stretched and the vaulter would release it to clear the bar. An IAAF requirement is that the vaulter must hold the pole in the grip area (no higher than 0.1524 m from the top of any pole or no lower than 0.4572 m from the top of the pole).

abaqus’ connector elements allow constraints involving relative motion of the connected parts via Lagrange multipliers as additional solution variables and also failure of the connection [15]. Through the connector element, a relative position of the point mass was given as a constraint on the upper tip of the pole. Moreover, the connector elements were employed as a sensor to measure the position \([x_{\mathrm {p}},y_{\mathrm {p}}]^{T}\) of the upper pole tip and the height \(h_{m}\) of the mass center. A user subroutine UAMP was used in each increment of the calculation to call the quantities measured by the sensors and enforce relative displacement components [16].

In the UAMP routine, the pole angle \(\varphi\) and the relative height \(h_{m,\mathrm {rel}}\) of the mass center were calculated via

$$\begin{aligned} \varphi =\arcsin \left( \frac{y_{\mathrm {p}}}{\sqrt{x_{\mathrm {p}}^{2}+y_{\mathrm {p}}^{2}}}\right) \quad \text {and}\quad h_{m,\mathrm {rel}}=\frac{h_{m}}{L}. \end{aligned}$$
(3)

As the sensor measurements are from the beginning of the time increment, the corresponding values of \(\varphi\) and \(h_{m,\mathrm {rel}}\) at the end of the time increment were extrapolated. Subsequently, the relative position of the point mass in coordinate system \(x_{2}\)–\(y_{2}\) in the next time step was determined as:

$$\begin{bmatrix} x_{m}\\ y_{m}\\ \end{bmatrix} = {\left\{ \begin{array}{ll} f(\varphi )\qquad &\text {if}\qquad \varphi \le {60^\circ }\\ f(h_{m,\mathrm {rel}})\qquad &\text {else}, \end{array}\right. }$$
(4)

depending on the simulation state being in the first or the second part of the vault. Here, f is a function that interpolates the relative position of the point mass from the discrete values of the different phases that were obtained in Sect. 2.1. The values calculated with Eq. (4) were further used as an input to feed-forward control the relative motion of the point mass. The UAMP was employed to enforce the relative motion of the point mass until a relative height \(h_{m,\mathrm {rel}}\) was reached, corresponding to the instance when the pole was completely recovered. Then, the connector fails corresponding to the vaulter releasing the pole. The push-off motion of the vaulter is negligible compared to the catapult effect of the pole [17]—regarding the current accuracy of the model. For a fully detailed model, the push-off angle of the vaulter should be taken into account. Eventually, the point mass moves freely under the influence of gravity only.

2.4 Initial and boundary conditions of pole vaulting

Regarding the boundary conditions of the simulation, the pole was supported at the lower end fixing all translational degrees of freedom. This represents the contact to the planting box. Furthermore, a gravitational acceleration of \(g=9.81\,\mathrm{m\,s}^{-2}\) was assumed.

The choice of the initial conditions is not trivial and has to be done carefully. Frequently reported in the literature, is the employment of only the take-off velocity \(v_{0}\) on the vaulter (see e.g., [9, 11, 18]), while no initial velocity was applied to the pole. The initial velocity of the vaulter is split into two components: one in the horizontal direction due to the approach speed and one in the vertical direction due to the jump. The components are calculated with the take-off angle \(\alpha\). Table 3 summarizes exemplary values for initial conditions according to Linthorne [18].

Table 3 Initial conditions of the simulations
Full size table

Due to the ‘hard contact’ boundary condition at the lower end, such an initial condition results in artificial oscillations of the pole with large amplitudes. All modes of the pole, which is initially at rest, are excited by the impulse. To circumvent these artificial oscillations, we started the simulation at the instance right after the pole was planted and when it started to bend as the vaulter’s mass compressed it. Then, in addition to the initial velocity of the point mass, also a velocity profile \(v_{0,\mathrm {pole}}\) on the pole was necessary that induced the bending. This profile was obtained from a preliminary simulation.

In this preliminary simulation, only the take-off velocity \(v_{0}\) of the point mass was applied as an initial condition and the density of the pole was artificially reduced by six orders of magnitude. Therefore, the oscillations still occurred in the beginning of the simulations but the amplitudes were small since the pole had nearly no inertia associated with it. In the following, the oscillations decayed quickly (approximately 0.01 s) and a homogeneous velocity profile developed in the pole (cf. Fig. 6).

Fig. 6
figure 6

Initial and boundary conditions of the simulation. The initial velocity profile is computed in a preliminary simulation

Full size image

The profile has velocity components in the horizontal and vertical directions and is not necessarily perpendicular to the pole. This profile was then extracted and employed as the initial condition for the simulation. The velocity profile’s shape resembles the bending of the pole in its first mode. Thus, an initial velocity profile initiates the real deformation. In the pole vaulting simulation, the profile was approximated with a third order polynomial along the pole length L requiring:

  1. 1.

    Zero velocity at the lower end,

  2. 2.

    Velocity at the upper tip equals the preliminary simulation,

  3. 3.

    Maximum velocity node position matches the preliminary simulation, and

  4. 4.

    Maximum velocity value equals the preliminary simulation.

3 Results and discussion

Figure 7 illustrates sequential frames of the pole vault simulation. We investigated the influence of the effective bending stiffness \(EI_\mathrm {eff}\) on the achievable vaulting height. The elastic modulus E was varied from 30 to 45 GPa (resulting in an effective bending stiffness range of 1822.42–2733.63 N \(\mathrm m^2\)) while all other material and geometry parameters of the pole were kept constant.

Fig. 7
figure 7

Deformation of the pole and motion of the point mass: The point mass is depicted by a blue square. The thin orange line indicates the coupling of the point mass to the pole via the connector element and, by that, its relative movement. The trajectory of the point mass is illustrated by the dotted line. After the pole is recovered and the vaulter releases the pole, only the point mass is shown (color figure online)

Full size image

IAAF [19] demands the crossbar, that needs to be cleared, to be straight above the planting box or up to 0.8 m behind it. Thus, in the x–y coordinate system from Fig. 2, the vault height \(h_{\mathrm {max}}\) should be attained at an x-position in the range of 0.0–0.8 m. Therefore, pole vault attempts, where the x-position of the vaulter at the vault height \(h_{\mathrm {max}}\) is negative, are considered to be a failed trial. Figure 8 depicts the maximum heights \(h_{\mathrm {max}}\) of the point mass depending on the effective bending stiffness \(EI_\mathrm {eff}\). Valid trials are indicated with a green square whereas failed trials are displayed with a red triangle. The general trend of a higher effective bending stiffness leading to an increased height is observable. However, if the pole is too stiff, the vaulter is not able to bend the pole in such a way that he is catapulted forward-leading to a failed approach. The x-position at the height is illustrated in addition to signify valid and failed trials. The maximum height that is achieved in a valid trial is \(h_{\mathrm {max}}={7.58}\,\mathrm{m}\) with an effective bending stiffness of the pole of \(EI_{\mathrm {eff}}={2218}\,\mathrm{N\,m^2}\), corresponding to an elastic modulus of \(E={36.52}\,\mathrm{GPa}\). Considering that only the vaulter’s body, but not his/her center of gravity, needs to pass the bar, slightly higher heights are possible. External circumstances as well as the fact that an athlete is never a perfect machine will decrease the realistic value. These results correspond well with world records. However, since dissipative effects are neglected, the computed height is slightly larger. The kinetic energy dissipated in the form of heat through the vaulter’s muscles significantly influences the maximum height \(h_{\mathrm {max}}\) [18]. In addition, the vaulter dissipates energy with impact when the pole is planted. The impact forces increase with higher pole stiffness. Since the simulation starts after the pole planting, this dissipation is as well neglected which especially influences the simulation outcome with poles of higher stiffness. Moreover, energy is dissipated due to friction at the planting box and the viscoelastic properties of the pole [20]. Further no force and momentum restrictions were considered for the relative movement of the mass point, meaning limits of human muscular strength are neglected at this stage. Essentially, computational simulations can compare different poles (i.e., different materials, lengths) as well as support the development of new poles.

Fig. 8
figure 8

Maximum height \(h_{\mathrm {max}}\) of point mass and corresponding x-position depending on the effective bending stiffness \(EI_{\mathrm {eff}}\) of the pole material

Full size image

The velocity of the point mass is displayed in Fig. 9. The velocity \(v_{x}\) in the horizontal direction decreases in the beginning as the kinetic energy of the approach is transferred into strain energy by deforming the pole. Subsequently, the velocity \(v_{y}\) in the vertical direction increases when the pole recovers to catapult the vaulter. After releasing the pole, the horizontal velocity \(v_{x}\) is constant since no forces act on the point mass in that direction. Contrary, the upward vertical velocity \(v_{y}\) of the vaulter decreases linearly under the effect of gravity. When the vertical velocity \(v_{y}\) decreases to zero, the maximum height \(h_{\mathrm {max}}\) and accordingly the maximum potential energy is reached. The energy transformations correspond well to the experimentally based descriptions of Dillmann and Nelson [21]. The simulated velocities correspond well in trend and magnitude to the measured ones of Frère et al. [4] and Angulo-Kinzler et al. [22].

3.1 Finite element choices: continuum vs. beam elements

The aim of this contribution was to allow for more detailed material models taking into account the heterogeneity of fiber-reinforced plastics. If the pole’s heterogeneous microstructure is to be taken into account, continuum elementsFootnote 6 need to be applied. They are computationally more costly, but distributions of field variables can be identified precisely and they allow to account for a sophisticated microstructured material model at a later stage.

If the underlying pole material is treated as a homogeneous continuum, the pole can be discretized with beam elementsFootnote 7. The use of beam elements is suitable since the pole has only one dominant dimension whereas the other two are relatively small. The advantage of this approach is its computational cheapness allowing fast model studies. Thus, beam elements were used for the simulations in the effective bending stiffness study performed in this work and the microstructure was neglected. For reasons of comparison, the performance of beam vs. continuum elements is illustrated exemplarily for one case in Fig. 9.

Fig. 9
figure 9

Velocity of point mass over time. Discretizations with (1) beam and (2) continuum elements

Full size image

4 Conclusion

This study provides a framework for FE simulations of pole vaulting, suitable for investigations on the pole’s material. The vaulter was accounted for as a point mass to save computational effort in control that was necessary in other studies. The motion of the vaulter relative to the pole was implemented with an algorithm based on a reference vault of an elite pole vaulter. The focus was on the proper choice of boundary and initial conditions to avoid unphysical oscillations. An initial velocity profile of the pole was determined by running a pre-simulation with reduced pole weight and overcomes unnatural simulation outcomes.

Beam elements as well as continuum elements can be used for the discretization of the pole yielding similar results. Continuum elements give a more detailed insight in distributions of field variables such as stresses and strains. Furthermore, they provide the option to study and incorporate complex computationally expensive material models considering the micromechanical structure of the pole.

The simulation results resemble measurements of the pole vault process in trend and magnitude. Additionally, we examined the influence of the effective bending stiffness of the pole on the achievable height in pole vaulting using an isotropic Neo-Hookean (continuum elements)/linear elastic (beam elements) material model and varying the elastic modulus. We observed that up to a certain stiffness, higher effective bending stiffness leads to higher pole vaulting heights. However, overly stiff poles would not bend enough to catapult the vaulter forward leading to failed vault attempts. This naturally occurring phenomenon is well reflected in our model.