Investigation of Spatial and Temporal Salinity Distribution in a River Dominated Delta through Idealized Numerical Modelling

Abstract

The world’s river deltas are increasingly vulnerable due to pressures from human activities and environmental change. In deltaic regions, the distribution of salinity controls the resourcing of fresh water for agriculture, aquaculture and human consumption; it also regulates the functioning of critical natural habitats. Despite numerous insightful studies, there are still significant uncertainties on the spatio-temporal patterns of salinity across deltaic systems. In particular, there is a need for a better understanding of the salinity distribution across deltas’ channels and for simple predictive relationships linking salinity to deltas’ characteristics and environmental conditions. We address this gap through idealized three-dimensional modelling of a typical river-dominated delta configuration and by investigating the relationship between salinity, river discharge and channels’ bifurcation order. Model results are then compared with real data from the Mississippi River Delta. Results demonstrate the existence of simple one-dimensional and analytical relationships describing the salinity field in a delta. Salinity and river discharge are exponentially and negatively correlated. The Strahler-Horton method for stream labelling of the delta channels was implemented. It was discovered that salinity increases with decreasing stream order. These useful relationships between salinity and deltas’ bulk features and geometry might be applied to real case scenarios to support the investigation of deltas vulnerability to environmental change and the management of deltaic ecosystems.

Introduction

Worldwide, half a billion people are currently dependant on deltaic ecosystems. Deltaic deposits are highly fertile regions, desirable sites to perform rural and agricultural activities as well as the centre of other numerous anthropogenic activities. River deltas are extremely vulnerable to both anthropogenic and natural changes such as sea level rise, variations in riverine flow, and changes in land-use practices (e.g., Paola et al. 2011; Syvitski et al. 2009; Fagherazzi et al. 2015). Continuous efforts are thus required to support the management and sustainability of these delicate ecosystems.

A possible direct consequence of environmental change is an increased salinity in deltaic regions. Increased salinity concentrations can have a severe impact on the anthropogenic activities taking place in river deltas and cause ecological degradation. For instance, increased salinity levels can damage soil cultivation, decrease the quality and availability of water for irrigation and human consumption (Lowell 1964; Smedema and Karim 2002), cause harmful algal blooms (Rosen et al. 2018), threaten livelihood, and compromise food security (Khanom 2016; Abedin Md et al. 2013). Increased salinity is currently endangering plant succession, wildlife, and fisheries dynamics in the Louisiana’s river deltas (Mississippi, Atchafalaya, and Wax Lake Deltas) (Holm and Sasser 2001), Ganges-Brahmaputra delta (Yang et al. 2005; Rahman Md et al. 2015; Karim et al. 1990; Mondal 1997) and in the Mekong Delta (CGIAR Research Centres in South East Asia 2016). Salinity distribution in coastal systems, including river deltas, depends on atmospheric, ocean and riverine forcing (Gong and Shen 2011). When fresh water from the upstream river mixes with the oceanic water downstream, the density differences in the water column induce a gravitational circulation. The competition between river discharge and ocean forcing determines whether mixing or stratification will prevail at different time scales. In the case of a river dominated system, the river flow has a dominant influence on the salinity (Valle-Levinson and Wilson 1994; Wong 1995; Monismith et al. 2002).

Concerns over water resources policy are one of the consequences of impacts of environmental and anthropogenic changes on deltaic systems, such as increased salinity. There is therefore a need for developing simple prognostic methods and tools to support decision and policy making. Even though the salinity field in estuarine systems has been extensively studied, relatively few studies have focused on the spatiotemporal distribution of salinity in river dominated deltas. The relationship between salinity and river flow has been studied indirectly by examining either the time lag of estuarine responses to river forcing (Kranenburg 1986; MacCready (1999, 2007); Chen et al. 2000; Hetland and Geyer 2004; Lerczak et al. 2009; Chen 2015) or the salt intrusion response to river flow changes (Monismith et al. 2002; Bowen and Geyer 2003; Gong et al. 2012). A direct negative correlation between salinity and river discharge has been demonstrated (e.g. Garvine et al. 1992; Denton and Sullivan 1993; Wong 1995; Peterson et al. 1996), but its applicability and validity have yet to be verified for deltaic systems. A major goal of the present study is to show that simple analytical solutions developed in the past to describe estuarine physics are also applicable to river-dominated deltas. A second objective is to support detection of delta areas at risk from salinisation using a channel classification based on stream orders, which has yet to be applied to the specific problem of salt distribution in delta channel networks.

The classification of channels in river networks by stream order was first introduced by Horton (1932, 1945) and revised later by Strahler (1952). It is a powerful technique that sets a hierarchy in branching networks with many tributaries. Despite the existence and development of other schemes such as Scheidegger-Shreve, Milton-Oiller and STORET (Ranalli and Scheidegger 1968; Gleyzer et al. 2004), it is usually preferred in hydrology and geomorphology studies (e.g. Beer and Borgas 1993; Tarboton 1996; Dodds 2000;Cole and Wells 2003; Raff et al. 2003; Reis 2006) because of its simplicity (Smart 1968; Moussa 2009). For example, many authors find it as a useful technique to be incorporated to the geomorphologic instantaneous unit hydrograph (GIUH), (Gupta et al. 1980; Rosso 1984; Gupta and Mesa 1988; Rinaldo et al. 1995; Rodriguez et al. 2005; Kumar et al. 2007; Lee et al. 2008; Moussa 2009). The Strahler-Horton method has also been implemented in many different areas such as statistics (Kovchegov and Zaliapin 2017, 2020; Yamamoto 2017), neuroscience (Pries and Secomb 2008), computer science (Kemp 1979;Devroye and Kruszewski 1994;Nebel 2000;Chunikhina 2018), biology (Borchert and Slade 1981) and social sciences (Arenas et al. 2004). In this work, an effort is done to adapt it for deltaic systems and test its application to the issue of salinisation of delta channel networks. Such an approach can be advantageous for many reasons. River deltas are subjected to tremendous dynamic changes under the influence of natural and human factors and undergo alterations across a wide range of spatial and temporal scales (Zhang et al. 2015; Passalacqua 2017). By implementing a hierarchy scheme to the treelike structure of a delta, scale-dependence can be overcome (Albrecht and Car 2004; Phillips 2016). For example, the Strahler-Horton scheme can summarize spatial and temporal variabilities in river basins despite variations in size (Rodriguez-Iturbe and Rinaldo 2001). A complex natural system (i.e. a system that exhibits structural and functional modularity) is usually hierarchically organized (Wu and David 2002). River deltas display great complexity in channel network structure (Sendrowski and Passalacqua 2017). The set of nodes and links connecting the channels of a network is termed as connectivity (Passalacqua 2017). Connectivity can become important when studying the complexity and evolution of landscapes and/or the interaction between external drivers and system’s variables (e.g.in this case, fresh water flow and salinity respectively) (Miller et al. 2012; Bracken et al. 2013; Sendrowski and Passalacqua 2017). This kind of analysis is considered a key element for water management decisions and hydrologic prediction (Western et al. 2001; Bracken et al. 2013; Passalacqua 2017). The stream order method that incorporates all these elements, can be thus extremely useful towards this direction.

In this study, we implement the DELFT3D modelling suite to numerically simulate hydrodynamics and the salinity field for an idealized river-dominated delta. The resulting model data are used to investigate and produce correlations between salinity and delta’s features. Field data from the Mississippi river enable a qualitative comparison with the model results.

Methods

DELFT3D (Deltares 2013) comprises a series of modules to carry out hydrodynamic, morphological, and water quality simulations. DELFT3D-FLOW solves the Navier-Stokes equations for an incompressible flow under the shallow-water and Boussinesq assumptions. Scalar transport (e.g. salinity or temperature) is calculated following an advection-diffusion equation:

$$ \frac{\partial S}{\partial t}+u\frac{\partial S}{\partial x}+v\frac{\partial S}{\partial y}+w\frac{\partial S}{\partial z}={K}_h\frac{\partial^2S}{{\partial x}^2}+{K}_h\frac{\partial^2S}{{\partial y}^2}+{K}_z\frac{\partial^2S}{{\partial z}^2}+ Ss $$

(1)

where K_h is the horizontal and K_z the vertical diffusion coefficient and Ss are source and sink terms.

In a 3D case, horizontal diffusion is resolved by the contribution of a 3D turbulence closure model and a user defined coefficient accounting for any unresolved horizontal mixing. In our model, this coefficient is constant and equal to its default value (10 m/s²) securing the model stability. The selected κ-ε turbulence closure scheme is a two-equation turbulence closure model in which the viscosity (and thus diffusivity) are determined from the turbulent kinetic energy κ and turbulence dissipation rate ε each calculated from a transport equation. The vertical diffusion is exclusively resolved by the turbulence closure model.

The Equation of State calculates the density ρ as a function of temperature and salinity. By default, DELFT3D uses the UNESCO formulation (UNESCO 1981). DELFT3D has been successfully implemented in the past for several applications including the modelling of river deltas, fresh water discharges in bays, stratified density flows and salt intrusion problems (de Nijs and Pietrzak 2012; Hu and Ding 2009; Elhakeem and Elshorbagy 2013; Martyr-Koller et al. 2017). For more details on the numerical model, a detailed description of DELFT3D can be found in the manual (Deltares 2013).

Model Setup

Model Bathymetric Setup

A morphological simulation was initially conducted to create an idealized river delta configuration. The morphology was then “frozen” and maintained constant during the investigation of the salinity field. The model domain has a rectangular grid of 4 km by 4 km. The grid resolution is 20 m in both x and y directions. A finer resolution of 10 m is adapted close to the inlet area to improve accuracy (Fig. 1). The river inlet is 400 m long and 200 m wide. The riverine input used for the creation of the morphology included both cohesive and non-cohesive material in equal percentages. Sediment characteristics and grain sizes were chosen according to findings from morphological studies with idealized modelling (Edmonds and Slingerland 2010; Caldwell and Edmonds 2014) so that a semi-circular delta shape was produced accompanied by a high bifurcation order. For this morphological simulation, the model was forced by a constant flow discharge of 900 m³/s. By setting a morphological factor equal to 70, the bathymetry in Fig. 1B is obtained after a simulation period of 5 days. The created morphology was then introduced as the input bathymetry for the salinity simulations.

Fig. 1

A) Model grid. The colours indicate grid cell area. The grid resolution becomes finer in the vicinity of the river inlet. White colour indicates inactive grid cells. X and Y are the coordinates of a Cartesian reference system. B) Bathymetry of the idealized river delta. Negative values in white colour denote land (inactive grid cells).The red line delineates the border between the delta and the ocean. It is defined as the line connecting interdistributary areas between channels with no branches where they meet the sea. Results analysis is done for the area upstream of this borderline. Semicircles S1, S2, S3 and S4 mark the areas where the salinity averaging is done in section 3.3. ϕ is the angle of the semicircles’ radius r with the horizontal r_o along the delta. A’ is the common centre of the semicircles colormap (Thyng et al. 2016) C) A sketch with the Strahler-Horton number assigned at each delta channel. Colours represent different stream order number. The stream order number decreases downstream with each channels bifurcation. Channels with no branches are 1st stream order. D) The flow hydrograph implemented in the model simulation. Vertical lines indicate the borders between the wet season and two dry seasons (one preceding and one succeeding). E) Monthly salt flux as calculated in section 3.1

Salinity Simulations Setup and Model Initialization

Four sigma layers in the vertical direction were used for the simulation of the hydrodynamic and salinity field. A sensitivity test on the number of sigma layers was done by implementing the model with 6 and 8 layers. Indicative numerical results are included in Appendix B and show that the impact of increased vertical resolution is small, probably due to the very shallow nature of the delta, and does not alter the overall conclusions of the study. Further taking into account computational resources required for a full year of simulation, we considered 4 vertical layers sufficient in the present case.

The flow hydrograph for the idealized model is constructed based on real data from the Mississippi River Delta. The Mississippi river daily discharge of the year 2017 (available on the usgs.gov website, station 07374000) is used. The Mississippi 2017 hydrograph displays an approximate Gaussian distribution with a peak in May. To remove wiggles and irregular fluctuations the beta (B) function is implemented in order to get a new distribution. The B function is given as (Yue et al. 2002):

$$ {\displaystyle \begin{array}{c}\mathrm{B}\ \left(\mathrm{a},\mathrm{b}\right)={\int}_0^1{\mathrm{x}}^{\mathrm{a}-1}\ {\left(1-\mathrm{x}\right)}^{\mathrm{b}-1}\mathrm{dx}\\ {}0<\mathrm{x}<1;\mathrm{a},\mathrm{b}>0.\end{array}} $$

(2)

where x is variable (the river discharge in this case) and a, b are parameters of the beta probability density function that determine the shape of the variable’s distribution. The distribution becomes Gaussian when the parameters are equal. The value of the coefficients determines the sharpness of the hydrograph’s peak which becomes sharper for high parameters values. The implementation of the B function ensures that the Gaussian hydrograph volume is equal to the Mississippi. However, this flow rate had to be scaled down to ensure the model’s stability. This is done by keeping the ratio of the flow rate to the channel’s cross-sectional area equal between the real and idealized delta. Fig. 1D shows the hydrograph implemented in the model. It is symmetric with a peak discharge between June and July and minimum values at the start and the end of the year. Note that the exact timing of the hydrograph within the calendar is arbitrary. The Gaussian function shape is desirable because of its simplicity. It provides a single high peak which allows easy distinction between wet and dry seasons. It might be easier then to detect correlations such as between the river discharge and salinity that would be difficult to discover when using a hydrograph of a more complicated shape. Nevertheless, it can be easily converted to other simple statistical distributions. Apart from the Mississippi river delta, normal flow distributions can be found in other real cases. The Yangtze River Delta (Chen et al. 2001; Lai et al. 2014) and the Swan Estuary in Australia (Kurup et al. 1998; Stephens and Imberger 1996) are examples of water systems demonstrating annual hydrographs often following normal distribution. A spin-up simulation is setup prior to the main one to get initial conditions. The minimum river discharge of Fig. 1D hydrograph is implemented in the model with the salinity set equal to 30PSU which is the typical offshore salinity in the Mississippi River Delta. A spin-up run for a period of one month was sufficient to achieve a salinity dynamic equilibrium under the influence of the minimum river discharge that remains constant in the model. The output is introduced as input for salinity initial conditions to the one year simulation.

Boundary Conditions

A constant water level is prescribed at the offshore boundary as the main focus of our model was to investigate the discharge-salinity relationship and the relationship between salinity and channel order for a river dominated case. For simplicity, the impact of tides and waves has been thus neglected. The offshore boundary is considered to be a sea boundary with salinity equal to 30 PSU. A Riemann condition is implemented at the lateral boundaries and free transport is allowed to let the model calculate its own hydrodynamic and transport values. The salinity at the river boundary is set to zero. The numerical simulations used to determine the salinity field do not include any mobile sediment input from either the river or the delta bed. The influence of sediments on the baroclinic flow is therefore neglected and the bathymetry is frozen during the simulation. The time step in the salinity simulation is chosen to be 1 min as the optimum value for both model stability and computational time.

Results

Salinity Distribution and Salt Fluxes

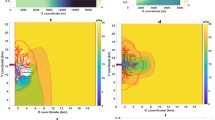
The salinity distribution computed by the model varies seasonally depending on the river discharge. Figure 2 presents maps of monthly averaged salinity field and flow vectors for the driest (December) and wettest (June) months, for both the top and bottom layers. The hydrograph is symmetrical, results for the first and second dry season are identical and here we only show results for the second dry season. Inside the delta, the mean top layer depth is 0.15 m and 0.5 m at the bottom layer. Maps for every month and all layers can be found in appendix A. The salinity maps highlight a fresh water area, the extent of which varies between dry and wet season on a monthly basis. In this paper, fresh water area refers to all areas where salinity is less than 2 PSU both in the delta channel network and offshore of the delta. Salinity equal to 2PSU is chosen as a threshold of impact to human activities and aquatic life following Kimmerer and Monismith 1993; Denton 1993; Andrews et al. 2017 (see also section 3.2). There are significant similarities between the fresh water area as defined in this paper and buoyant plume structures as defined in estuarine systems. However, the river input in the present setup flows first into a deltaic zone (see Fig. 1B), where fresh water movement and any plume development are strongly constrained by the complex bathymetry. Therefore, we choose to restrict the use of the term plume to the regions offshore of the delta. During the dry season (exemplified in Fig. 2A, C), fresh water (in dark blue colour) is restricted within a narrow area around the river inlet. Salt intrusion in the inlet is indicated by the upstream direction of the flow vectors and by the clustering of isohalines inside the river channel in Fig. 2C. In contrast, results for the wet season (Fig. 2B and D) clearly indicate the formation of an offshore buoyant plume: top layer salinities are reduced throughout most of the domain while bottom layer salinities still show a sharp horizontal gradient around the delta limit. In both cases, salinity in the delta is much lower than the high oceanic values observed offshore. The river flow maintains salinity inside the delta within a specific range. Especially during wet season, the salinity remains below the 2 PSU threshold in a large part of the delta.

Fig. 2

Monthly averaged salinity and flow vectors at (A) driest month at the surface (B) wettest month at the surface (C) driest month at the bottom and D) wettest month at the bottom. White areas indicate dry points and delineate the channels borders. The isohalines are at 1 psu salinity increment. Grid spacing for flow vectors is 10. colormap (Thyng et al. 2016)

Figure 2 also presents monthly-averaged flow vectors. The boundary conditions for water elevation, currents, and salinity help generate a baroclinic circulation pattern in the numerical domain: top layer flow vectors indicate an offshore directed flow while the bottom layer flow vectors indicate onshore directed flow. This circulation pattern remains present during both dry and wet periods but its strength appears to be modulated by the river discharge (stronger during wet season). This circulation is an important aspect of the modelling as it provides a critical mechanism for onshore salt flux.

The salt flux M_sin the model is calculated following Jia and Li (2012):

$$ {M}_s=\sum \limits_{i=1}^n{S}_i\ast {A}_i\ast {V}_i $$

(3)

with S, A and V the salinity, area and flow velocity respectively of grid cell i and n the total number of grid cells. Monthly salt flux values are presented in Fig. 1E. Negative flux values for the first six months indicate a loss of salt across the model domain. From January (start of the simulation) and until July, the flow rises continuously. As a result, the seaward advection increases causing a decrease of salinity concentrations. On the contrary, from July until the end of the year, the flow declines. As the salinity is constantly 30 PSU at the offshore boundary and because the lateral boundaries do not preclude salt flux, the salinity at this stage increases and its flux becomes positive. It can be seen that the biggest impact of the fresh water flow to the salt mass occurs during the transitional periods between dry and wet season. Salt fluxes are maximum in April (out flux) and September (influx) while they are minimal during the minimum discharges months (January and December).

Flushing Time

The system’s response to the fresh water influence is examined by calculating flushing times. Flushing time (FT) is usually defined as the time required to replace the fresh water volume of a water body (e.g. river delta, bay, and estuary) with the river discharge (Dyer 1973). The FT was calculated following (Sheldon and Alber 2002):

$$ FT=\frac{\sum \limits_{i\kern0.75em }^n\left(\frac{S_W-{S}_I}{S_W}\right){V}_I}{Q_F} $$

(4)

where V_Ithe grid cell volume, S_w is the seawater salinity at the offshore boundary (30 PSU), S_I is the salinity at each grid point and Q_F the fresh water flow averaged within a certain period. Equation 4 is implemented exclusively to the delta area in the model as defined by the red coloured borderline in Fig. 1B. In the absence of tides the FT variation depends on the fresh water flow fluctuation. In our test case, river discharge is highly variable ranging from periods of very low to periods of very high flows. As a result, the calculation of an instantaneous FT showed high variation during the simulation and could not give a reliable and indicative estimation of the time needed by the system to become fresh in dry and wet seasons. It is preferred then to average the river discharge over longer periods. The determination of the appropriate averaging period is usually an important and difficult issue when calculating FTs.

Various approaches exist for determining the fresh water flow or discharge from using mean monthly or seasonal discharges (e.g., Pilson 1985; Christian et al. 1991; Lebo et al. 1994), where the mean is taken from long-term records covering many years, to observational discharges, to discharges time-averaged over a user-defined recent past period (e.g. Balls 1994; Eyre and Twigg 1997). Here we investigate FTs for the two dry trimesters (January–March and October–December) and the two wet trimesters (April–June and July–September) so the average river discharge of each trimester is taken. A comparison was also done between dry and wet seasons preceding (1st semester) and succeeding (2nd semester) the peak flow. Results can be seen in the bar graph of Fig. 3. It was found that more than 2 days are needed for the river flow averaged during dry months to renew the waters while the same process is much faster during the wet months when the FT is less than 6 h (<0.25 days). Interestingly, the FT between the two dry periods (first and last trimester) is a bit smaller during the last trimester even though the discharge range between the two trimesters is the same. This drop may be due to an influence of antecedent flow since one of these trimesters is preceded by a wet period flushing completely the delta.

Fig. 3

Flushing times calculated with a trimester averaged river discharge

Because the use of an average discharge over a long period might be misleading, the date specific method (DSM) is implemented for comparison as introduced by Alber and Sheldon (1999). According to this, the discharge averaging period must be equal to the flushing time itself. An iterative process is then used that starts with a discharge that refers to a starting observation day. The FT calculation is then worked backwards until the averaging period is the closest to the flushing time.

We select two days to be our starting observation point. First, the day of the peak flow and then the day when the minimum flow occurs at the end of the simulation. After the determination of the averaging period, the FT is calculated for the mean and the median discharge for both cases. The mean and median FTs are equal for the maximum flow (0.13 days ~3 h) indicating that the process is very fast at the highest discharges. However, when the time of minimum flow is the starting point, these two numbers differ significantly. The mean flushing time is ten times smaller than the median (17 days and 168 days respectively) because it mitigates the influence of the very low discharges that are present at the end of the simulation. Table 1 shows results for the DSM.

Table 1 Flushing times (FT) of the Date Specific Method

The calculation of FT with the DSM indicates an underestimation of the dry period times and an overestimation of the wet period ones when averaging in trimesters. When the DSM is implemented for the peak discharge, the averaging period is only one day since the water can be renewed very fast in such high discharges. As a result, the median and mean FT with the DSM method are equal because the median and mean discharges for only one day are also equal. This FT was found to be approximately the half of the seasonal one.

The seasonal averaged method overestimates FT because it modulates the effect of the maximum discharges. DSM shows much higher mean and median FT when the minimum flow day is taken as a starting point to find the appropriate averaging period. Mean FT is ~7 times higher in this case because both the averaging period (< 90 days) and the discharges are much smaller compared to their mean trimester values. Likewise, the median FT with the DSM is excessively high as a result of the fact that the median value is closer to the very low discharges at the end of the simulation.

The results of the DSM might be more realistic. Considering that low river discharges can sometimes be equal or even smaller than 0.1 m³/s in the simulation, flushing times between 2 and 3 days that were found from the seasonal averaging seem to be very small.

In addition to the FT calculation, it is important from a management point of view to identify the time period that salinity inside the delta exceeds specific values. Threshold salinity values determine the safety limits for different activities. For instance, drinking water is usually considered potable when salinity <1 psu (Ahmed and Rahman (2000); de Vos et al. (2016); Dasgupta et al. (2014)) while irrigation water with salinity >4 psu can cause severe reduction of crop yields (Clarke et al. 2015). Marine species present in estuarine habitats have limited tolerance to salinity. The location of the 2-PSU bottom isohaline (commonly denoted in the literature as X2) is considered as an important habitat indicator. X2 has significant statistical relationships with many estuarine resources (e.g. phytoplankton, larvae fish, shrimps, smelt etc.) (Jassby et al. 1995, Hutton et al. 2015). It is alternatively often used as a salt intrusion measure (Schubel et al. 1992; Monismith et al. 2002; Andrews et al. 2017). In addition, 2 PSU is a threshold for fresh water wetlands conversion to brackish marsh (Conner et al. 1997; Wang et al. 2020). This is especially true for the Louisiana wetlands and the Mississippi River Delta (Visser et al. 2013) where the majority of vegetation species (e.g. Sagittaria latifolia, Sagittaria lancifolia, Phragmites australis) survive in conditions less than 2 psu (White et al. 2019).

A critical value of 2 PSU therefore appears to be a sensible threshold that represents requirements for many to most delta ecosystem services. Figure 4 shows an estimation of the time required for salinity to exceed 2 PSU. The time is counted from the moment of highest discharge (hydrograph peak in Fig. 1D) to investigate how long the system remains fresh after a wet period. It can be seen that the number of days to surpass the 2 PSU limit decreases seaward. The flushing time is always smaller than the simulation time left after the wet period (180 days left from the peak discharge). Inside the river inlet, the area from the river boundary up to ~100 m downstream from the river boundary is always fresh and never exceeds 2 PSU including the deeper portions of the channel. Salt intrusion inside the river inlet starts to develop after approximately 4 months from the wet period when dry conditions recur. Downstream of the river mouth, salinity exceeds 2 PSU within 80–90 days from the wet period and further offshore salinity exceeds 2 PSU much faster and within two months from the wet period.

Fig. 4

The time (in days) that is needed for salinity to exceed 2 psu after the peak discharge (day 181, 1st of July). The maximum number of days (dark red) corresponds to areas where the water remains always fresh and below 2 psu. The minimum number of days (dark blue) corresponds to areas where salinity is always above 2 psu. White areas indicate dry points

Correlations of Salinity with River Discharge and Distance from the River

The salinity response to river flow fluctuations is investigated by looking at the relationship between salinity and river discharge imposed at the river boundary (Fig. 1D). Salinity spreads by approximately following semi-circular isohalines (Fig. 2). Salinities increase horizontally with the distance r from the river mouth and the angle ϕ with the x axis (Fig. 1B). The variation with ϕ is influenced by channels characteristics (location, length and width) which also impact isohalines symmetry. To derive simple analytical relationships despite the complex morphology, the depth averaged salinity is averaged within points of equal distance from the river mouth (with the centre at point A’, Fig. 1B). These points belong to imaginary semicircles whose radius r represents the distance from the river mouth. We perform this averaging within grid points that are located along the semicircles S1, S2, S3 and S4 of Fig. 1B. These semicircles comprise points at a distance of 250 m, 500 m, 750 m and 1000 m from the mouth respectively. Figure 5 shows these averaged salinity values as a function of the daily flow (Fig. 1D). Dry points (white colour areas in the maps of Fig. 2) are not taken into account in the averaging. This means that the salinity is in fact averaged over a sum of arcs with equal distances from the mouth (see section 4.1).

Fig. 5

Daily averages along the four semicircles shown in Fig. 1B of the depth averaged salinity against the river flow. Each curve displays average values within points of distance 250 m, 500 m, 750 m and 1000 m from the river boundary. The fitting lines are added with black colour and the determination coefficient (R²) is included in the legend

A regression analysis of the results shows a negative and exponential correlation between salinity and river flow for each of the four distances. The highest salinity values are close to the delta border with the sea and lower values are close to the river mouth. At a distance of 250 m from the mouth, the water becomes fresh when the river discharge exceeds approximately 40% of its peak value. At a distance of 500 m, a higher discharge is needed that should exceed 50% of its peak value to make water fresh. For a distance from the river mouth higher than 500 m, salinity largely declines with increasing discharge but the water remains brackish and salinity never reaches the zero value. Fitting of the results in Fig. 5 gives an exponential equation in the following form:

$$ \mathrm{S}=\upalpha \ast {\mathrm{e}}^{-\upbeta \mathrm{Q}} $$

(5)

S is salinity and Q the river discharge from Fig. 1D. The coefficient α has salinity units and increases seaward while the coefficient ϐ decreases seaward. The parameters values of each semicircle can be seen in Table 2. The fitting lines for each curve are added in black colour in the figure. The fitting lines match extremely well the discrete numerical data at a distance of 750 m and 1000 m, but minor deviations are present between the fitting lines and the data at 250 m and 500 m. This may be attributed to the presence of dry points that reduce the number of wet points available for averaging. The fitting was very good for each curve with a coefficient of determination R² ~ 0.99.

Table 2 Values of α and ϐ coefficients of the exponential equation (eq.5) for each curve in Figure 5

According to Fig. 5, the salinity unsurprisingly increases with distance from the river for all discharges so throughout the year. Temporal (annual) averages of the salinity further elucidate the relationship between salinity and the distance r from the river. For this purpose, we considered 15 radial sections every 125 m between 250 m and 2 km from the river mouth. The salinity averaged over the depth and radially (cross-sectional radial average) and over the full year is plotted against the distance r from the river (Fig. 6). The complex bathymetry causes the annual salinity to be slightly lower in two specific sections (i.e. 625 m, 1500 m) compared to their upstream neighbour one. Despite this, the spatio-temporally averaged salinity increases with the distance following a curve close to sigmoid (see the fitting approximation in Fig. 6) which may also be related to exponential forms. It is reasonable then to assume that the regression analysis solution (eq. 5) incorporates both river discharge and distance.

Fig. 6

Annual averages of salinity over radial sections against the distance from the river mouth. The averaged values seem to belong in a sigmoid function approximated by the thick blue line

This is an important outcome as it can provide us with information of the expected salinity levels in a delta when the fresh water volume is known. This solution is valid only under certain assumptions because it refers to a non-rotating case and it does not include tides or wind/waves driven mixing. The physical meaning of this equation and the corresponding coefficients together with its limitations are discussed further in section 4.1.

Correlations with Channel Bifurcation Order

A stream order number is assigned to each delta channel following the Strahler-Horton method (Strahler 1952). According to this, first order channels are those with no tributaries at all and second stream order (SO) channels begin at the confluence of two first SO channels. SO increases by one if a channel receives two channels of the same order. When a stream of a given order receives a tributary of lower order, its order does not change. The latter rule though had to be overlooked in several instances, due to the complexity of the delta which includes a variety of formations like closed networks where the method cannot be accurately implemented. In these instances, the stream order number also considers the channel’s depth and the number of junctions with neighbours. In our idealized delta, there are 18 channels of first order, 8 of second order, 4 of third order, 2 of fourth order, and one of 5th order (Fig. 1C). Most of the first SO channels are located at the end of the delta and in shallow areas while higher stream order channels are usually closer to the river channel. Nevertheless, stream order number is irrelevant of a channel’s position in the network and does not necessarily reflect its relationship with channels in a similar location (Hodgkinson 2009).For example, it can be seen in Fig. 1C that the two channels separating at the river mouth are not of the same order. Although someone would expect these two neighbour channels to be of equal order and have similar characteristics because of their proximity, this is not the case. The importance of the stream order labelling lies on the fact that it takes into account the channels connectivity which is higher in the south part (four joints at the 5th SO channel) than in the north (only three joints at the 4th SO channel). Knowing that with each bifurcation both the depth and river discharge decrease (Olariu and Bhattacharya 2006), it is obvious that the two channels would exhibit differences in their salinity levels despite their locality. The temporal evolution of the depth-averaged salinity averaged within channels of the same SO is shown in Fig. 7A. As expected, the time evolution is opposite to the hydrograph for every SO. Salinity increases as the channel stream order decreases and so higher salinity values are present in lower stream order channels. Second and third order channels have an equal minimum because of their geographical proximity. There is also a spatial trend for the duration that the water remains fresh. This amount of time is minimum in first order channels (~1.5 months) and increases upstream with the increase of the stream order number reaching a maximum of 5 months for the 5th stream order. Dry points (land) interfere with channels of 2nd, 3rd and 4th order. Some of them remain submerged after the wet period. This causes a small increase of salinity there during the second semester when a wet period has preceded.

Fig. 7

A) The evolution in time of the mean over depth salinity averaged within channels of the same stream order. B) The evolution in time of the potential energy anomaly (PEA) averaged within channels of the same stream order

Another important aspect to consider is stratification as it can act as a control on the dynamic evolution of salt intrusion. For example, an increase in river discharge can lead to increased stratification, which in turn may increase residual circulation and near-bed salt intrusion, thus weakening the relationship between salt intrusion and river discharge (e.g., Monismith et al. 2002; Ralston et al. 2008; Lerczak et al. 2009). Therefore, the stream order analysis is extended to include information on stratification. This is achieved by calculating the potential energy anomaly (PEA), which is the energy required to instantaneously homogenize the water column for a given density stratification (Simpson 1981; Burchard and Hofmeister 2008). According to this definition potential energy anomaly ɸ is equal to (Simpson 1981):

$$ \upphi =-\frac{1}{D}{\int}_{-H}^{\eta } gz\left(\overline{\rho}-\rho \right) dz $$

(6)

where $\overline{\rho}$ is the depth-averaged density, ρ is the depth-dependent density, H the mean water mean depth, η the surface water elevation, D the total water depth, g gravitational acceleration and z the vertical coordinate.

Figure 7B shows the PEA level when averaged within channels of the same stream order (SO) for the whole simulation period. During the dry season, PEA increases with the decrease of the SO and thus landward, which is related to the increase of channel depth with SO, since deeper channels are more likely to be stratified. The only source of energy to mix the water column in the present numerical setup is the river flow (in absence of ocean and atmospheric forcing), so it is not very surprising that the stratification levels overall decrease with increasing river flow. Increases in river flow also shift the position of the salt intrusion front (see Fig. 2) thus explaining some of the behaviour shown in Fig. 7B where stratified regions move seaward (decrease in SO). This leads to maximum PEA for small SO during the wet season.

There appears to be an important shift in the response of salinity and stratification to variable river flow between channels with SO 3 and above versus channel with S0 1 and 2. The increase in river flow is sufficient to completely mix channels with SO3, 4, 5 and result in constant salinity values over (most of) the wet period. In contrast, for channels with SO 1, 2, the increase in river results in an initial increase of stratification, consistent with many estuarine studies (Monismith et al. 2002;MacCready 2004; Ralston et al. 2008; Lerczak et al. 2009; Wei et al. 2017), before reaching a stage where the river flow is sufficiently high to mix the channels. However, in these two cases, the channels are also too far downstream for the river discharge to completely mix the water column and result in a constant salinity (not dependent of river discharge anymore).

Time averages of salinity curves in Fig. 7A produce annual averages per stream order which are presented in Fig. 8. The error bars denote the standard deviation due to the overall spatial variability of salinity in channels of equal order. As the SO decreases, the number of channels per SO increases. It would be expected then that higher SO values would exhibit lower standard deviation. However, the spatial variability of SO averaged salinity can be affected by the length and width of channels. This explains the larger variability for SO = 3 than for SO = 2, due to third order channels being longer (and in some cases even wider) than the second order channels (Fig. 1C). Even though the relationship portrayed in Fig. 8 appears to be consistent with an exponential function, the small number of stream orders (five in this case) makes a quantitative and conclusive regression difficult. Further considering bifurcation orders in natural systems (e.g. only three orders were identified in the Mississippi Delta, see section 3.5), it appears unlikely that a quantitative relationship would be meaningful and representative for a large number of real deltas. Instead, the main result ought to focus on the qualitative relationship that salinity increases with decreasing stream order.

Fig. 8

Annual salinity values averaged per stream order. The error bars indicate the standard deviation due to the spatial variability in annual salinities

Comparison with Real Data

In order to gain confidence in the veracity of the idealized numerical results we have presented, we compare them with real data available from the Mississippi River Delta and examine if similar trends exist in nature. The Mississippi River Delta is chosen for comparison because it is generally classified as a river dominated delta. We used maps with time-series of isohalines every fortnight and with step of 1 psu corresponding to measurements from 2017. These maps are provided by the Lake Pontchartrain Basin Foundation https://saveourlake.org/ within the purposes of the Hydrocoast Program. The Mississippi Delta channels were classified in three stream orders following again the Strahler-Horton method. The maps resolution allows us to identify and name 18 channels as it can be seen in Fig. 9. A mean salinity is assigned at every channel calculated as the average value of all the isohalines crossing through a channel for every fortnight (24 values per year). Monthly values are obtained then and salinity is again averaged within channels of the same SO as is done in section 3.4. Then, model results of Fig. 7A are also monthly averaged to make the comparison with the Mississippi data. The comparison can only be done for SO 1 to 3 as the bifurcation is lower compared to the idealized model. Figure 10A shows the monthly averaged model results for SO 1 to 3. Figure 10B presents the monthly averaged Mississippi data results for SO 1 to 3. The salinity has been normalized in both cases by dividing by its maximum value. The qualitative comparison with results from the idealized modelling is good since salinity increases with decreasing stream order in both cases. Salinity data is then processed in a manner consistent with the averaging undertaken previously to present the relationship between salinity and stream order: i.e. salinity values are time averaged over a year and spatially averaged to result in an annual salinity value for each stream order in the Mississippi (Fig. 11). The error bars indicate the standard deviation due to the spatial variability in annual salinities. The qualitative comparison with the results of the idealized model is once again satisfactory with stream order averaged salinity (and standard deviations) increasing (decreasing) with decreasing (increasing) stream order.

Fig. 9

Planar view of the Mississippi River Delta (Courtesy of https://www.google.com/maps/). The capital letters name the channels for which there is available data. Red colour classifies first stream order (SO), blue colour second SO and green colour third SO. The black circles are the reference points to measure distance from the river for every channel at each subdelta

Fig. 10

Monthly salinity values averaged within channels of the same stream order (SO) and normalized by their maximum in the A) idealized model and B) Mississippi Delta in 2017

Fig. 11

Mean annual salinity averaged within channels of equal order in the Mississippi Delta. Error bars indicate the standard deviation due to the spatial variability

The methods of section 3.3 are adapted to the Mississippi data and similar plots are reproduced. At first, the salinity is averaged in distances of 5 km, 10 km, 15 km and 20 km from the river. The distance is measured from the three black dots drawn in the main river branch in Fig. 9 for each one of the three Mississippi subdeltas. If there is no isohaline crossing exactly at some of these distances, then an interpolation is done between the first upstream and the first downstream isohaline with respect to that distance. Figure 12 presents the salinity-river discharge correlation at each distance from the river (i.e. 5 km, 10 km, 15 km and 20 km) for 2017. The averaged per distance salinity is plotted against the river discharge in Mississippi (available on the usgs.gov website, station 07374000). The river discharge measurements are time averaged to match the number of available salinity observations. These are 25 in total for 2017 (typically two per month but three for July). An exponential regression analysis is done and the R² coefficients are shown in Fig. 12. The goodness of fit for an exponential correlation is tested by implementing the Kolmogorov – Smirnov test. For a number of 25 samples, as is the number of observations here, the critical value for this test is 0.264 with a 5% uncertainty. If the test-value is below this threshold then the hypothesis that the data follow an exponential relationship can be accepted. An exponential relationship between salinity and river discharge is supported by the test values per curve (reported as ks in Fig. 12) for the data at 5 km. An exponential relationship is also supported for the 10 km data, but in this cases at a 10% uncertainty level (critical l value equal to 0.3165).

Fig. 12

Salinity observations of year 2017 in the Mississippi Delta against river discharge measurements of the same period. The observations are groupped and averaged within distances of 5 km, 10 km,15 km and 20 km from the river, denoted in the graph with different colour. The fitting lines of an exponential regression analysis are added.The determination coefficients (R²) for each case are included in the legend together with the kolmogorov – Smirnov statistical values (ks) per case. Note that the critical value for a number of 25 samples is 0.264 for a 5% uncertainty and 0.3165 for 10% uncertainty

It can be seen in Fig. 12 that the ks values increase with the distance. This expresses the decrease of the river influence with the distance and thus the decrease of the probability for an exponential relationship. In every case, the exponential fitting is weaker in the Mississippi Delta than in the idealized one. This discrepancy is not unexpected considering the numerous differences between the two systems. In the idealized model, we purposefully neglected the impact of tides and other hydrodynamic forcing (waves, storm surge etc.). Even though tidal forcing is weak in the river dominated Mississippi delta, it may still act as a mixing factor, thus weakening the river discharge influence on the most distant channels (usually of 1st stream order). In addition, the response of salinity to river discharge is likely to be affected by time lag and the system’s flow history (e.g. antecedent flow, Denton and Sullivan 1993; Andrews et al. 2017). It should also be noted that the Mississippi maps do not present information of salinity’s vertical distribution whereas the analysis with our model results is done for depth averaged salinity. The lack of salinity data in the vertical does not allow a PEA analysis for the Mississippi observations. A more detailed discussion for the inconsistencies between model and real data results for this case can be found in section 4.1.

Discussion

Salinity-River Discharge Relationship

The idealized model simulates the full three-dimensional baroclinic flow for a typical configuration where there is an upstream river boundary with a varying fresh water inflow and a constant sea boundary condition. In spite of a number of complex processes being accounted for in the idealized numerical model (e.g. complex delta morphology, dynamic flow variability, stratification), the numerical results are well approximated by an exponential relationship between salinity (depth averaged and averaged over arcs) and river discharge (i.e. equation 5).

Denton and Sullivan (1993) developed empirical antecedent flow-salinity relations which are similar to eq. 5. The exponential form arises from the solutions of 1D advection-diffusion equations for salt conservation under certain assumptions, initial conditions, and boundary conditions (Crank 1975; Fischer et al. 1979; Zimmerman 1988). In particular, solutions similar to eq. 5 are found under steady state conditions, for constant cross-sectional area, and for constant dispersion coefficient.

Our delta situation presents similarities and differences with such a simple case. The numerical model does use a constant horizontal diffusion equal to 10 m²/s, but the other two key assumptions are not a priori satisfied. That the numerical results remain well approximated by eq. 5 would seem to indicate that the system remains close to steady state, and therefore that the fresh-water discharge only varies slowly compared to the intrinsic salinity adjustment time scale of the system. The cross-section A used to average results is not constant, and does not vary monotonously with distance from the river because of the complex bathymetry and geometry of the delta. Nevertheless, the numerically derived flow-salinity relationship remains a good fit to an exponential. Such exponential solutions of the advection-diffusion equation have been presented even for non-steady and/or variable coefficients (and thus cross-sections).

For example, Phillip (1994) provided exponential solutions of the advection-diffusion equation in two and three dimensions for a radial flow in the case of variant diffusion coefficient and time-varying flow. Zoppou and Knight (1999) derived exponential solutions to the advection-diffusion equation for spatially variable diffusion and velocity coefficients. In both studies, analytical solutions are expressed only using constant coefficients terms after a series of mathematical transformations of the varying coefficients. It thus seems reasonable to pursue an analogy to the steady state, constant cross-sectional area, and constant dispersion coefficient case for explanatory purposes.

Following from our results, including the different values for the parameters in eq. 5 (Table 2), eq. (5) can then be rewritten as follows:

$$ \overline{S\left(r,t\right)}=\overline{S_{max}(r)}\ast {e}^{-\beta (r)Q(t)} $$

(7)

Where S the cross-sectional averaged salinity and the overbar denotes depth averaged values. The coefficient α corresponds to the maximum salinity when Q = 0. In other words, α is the maximum averaged salinity (S_max) in a distance r. In our specific case, the maximum salinity is also the initial one, since Q has values very close to zero at the start of the simulation according to the hydrograph (Fig. 1D). It is logical then that α increases as the radial distance from the mouth increases (Table 2). The coefficient β expresses the effect of distance on the river flow influence which explains why its values decrease as r increases (Table 2).

It is inferred then, that in a river dominated delta, the salinity at a certain distance from the river could be determined based on river discharge charts as Denton and Sullivan (1993) did for the San Francisco Bay, even in non-steady systems and for varying in space cross-sections. It is interesting that despite the non-uniform bathymetry and the unsteady conditions, the problem is successfully approximated with the above method. Since the results in section 3.3 take into account the full range of river discharges over the year, this approach remains valid for the entire simulation period even though the dynamics vary significantly due to significant variations in the fresh water discharge.

The domain undergoes important dynamical changes in time under the influence of the river discharge’s high variability in time. The Peclet (Pe) number is a non-dimensional parameter that can be used to monitor the time scales of advective and diffusive processes inside the delta. For a considered length scale λ, Pe can be calculated as:

$$ Pe=\frac{U\lambda}{K} $$

(8)

Where U is the fresh water velocity through the river boundary cross-section, λ the length of the inlet (400 m) and K the diffusion coefficient (10m²/s here). Figure 13 shows the Pe evolution in time during the simulation. For Pe values less than 1, transport is mainly the result of diffusive processes. This is the case during dry seasons. The horizontal dashed line in Fig. 13 marks the threshold of Pe = 1. The curve crosses the threshold for the first time approximately 90 days after the start of the simulation and again 90 days before its end. These two periods of 90 days with Pe < 1 correspond to the two trimesters of dry season (see also Fig. 1D). In between these two periods, Pe is larger than 1 which means that advection prevails inside the delta and diffusion becomes less important. This describes the conditions in the delta during the six months period of wet season.

Fig. 13

The Peclet (Pe) number evolution in time for a length scale λ equal to the river inlet length. The horizontal dashed line marks the limit between diffusion and advection dominated periods when Pe = 1. The vertical lines indicate the times when Pe surpasses or falls below 1 which corresponds to the start of the wet and the dry season respectively

Several past studies have pointed out the influence that lateral variations of depth, present in our model, have on the longitudinal salinity gradients (Li and O’Donnell 1997; Li et al. 1998; Uncles 2002). This is usually presented as an uneven distribution of vertical mixing causing significant lateral and vertical circulation (Dyer 1977; Valle-Levinson and O'Donnell 1996; Li and O’Donnell 1997). The impact of secondary flows on the along delta salt transport seems to be well incorporated in eq. 7 by the depth and radial averaging.

As noted previously, an exponential flow-salinity relationship is much less satisfactory for the Mississippi delta, which should not be entirely surprising given that the assumptions behind eq. 7 are far less likely to be valid in natural systems. A critical one is the constant dispersion coefficient (K) which is not a realistic assumption for natural systems. For example, K values in the San Francisco and Willapa bay vary in a range between 10 m²/s and 1000 m²/s (Monismith et al. 2002; Banas et al. 2004) while Fischer et al. (1979) summarize its range between 100 and 300 m²/s based on data from a series of estuaries. Monismith (2010) presents a list of mechanisms for predicting K values in real systems from observations. However, the assumption for a constant diffusion coefficient is a common practice in modelling studies. In their work for investigation of the dependence of the longitudinal salinity gradient on channel contraction and/or expansion, Gay and O’Donnel (2007) comment on the lack of theoretical reason for implementation of varying K in their model. Moreover, Lewis and Uncles (2002) found better agreement between their model and salinity observations with a constant rather than a varying K.

The uncertainty on the diffusion’s magnitude in a real system in addition to the external forcing present in the Mississippi delta could partly justify the weaker exponential fitting (Fig. 12).Furthermore, the eq. 7 describes a spatio-temporal salinity-flow distribution under important limitations. The exponential correlation is a direct outcome of the dominant role the river flow plays in the modelled case. The presence of other additional forcing mechanisms (i.e. wind, waves, along-shore transport) could alter this correlation because of the changes it would cause to the river flow direction and the fresh water layer shape, thickness and vertical structure. For instance, waves change the flow jet direction from the river mouth and affect its spreading. If the angle between the waves and the shore is high then it causes a deflection of the jet flow downdrift (Nardin and Fagherazzi 2012). Moreover, wave-induced transport causes changes to horizontal salinity gradients and may modify estuarine circulation (Schloen et al. 2017). Consequently, the isohalines would not exhibit symmetric and semi-circular shapes as they do in our model results (Fig. 2). A flow asymmetry would determine different fresh water areas modifying the results from averaging salinity in Fig. 5. We would expect differences to be more pronounced during dry seasons because wet seasons showed river-induced mixing conditions leading to zero salinities inside the delta irrelevant to flow direction (Fig. 2B and D).

Deviations from the simple exponential relationship may also arise from wind forcing intermittently impacting the baroclinic response of the system. For example, down-welling favourable winds constrain fresh waters onshore and increase plume thickness, while upwelling favourable winds tend to promote offshore spreading of fresh water and plume thinning (Barlow 1956; Pullen and Allen 2000; Fong and Geyer 2001; Whitney and Garvine 2005; Choi and Wilkin 2007). Wind forcing also impacts dynamics in estuaries modifying circulation and salt transport (e.g., Scully et al. 2005; Chen and Sanford 2009; Bolaños et al. 2013). Vertical mixing processes affect fresh water thickness too. For example, wave breaking at the surface leads to enhance mixing and more homogeneous plumes (Gerbi et al. 2013; Gong et al. 2018), while wave-induced circulation usually traps fresh water landward, reducing the surface salinity and increasing the fresh water thickness (Delpey et al. 2014; Rong et al. 2014).

Bifurcation Correlations

Channels classification schemes, such as the Strahler-Horton method implemented here, can be successfully used to relate the salinity with channels hierarchy: salinity increases seaward as the stream order number decreases. Lower salinity should be expected in parts of the delta with higher number of channels junctions which are usually located closer to the fresh water source. Both river discharge and channels depth typically decrease with each bifurcation (Olariu and Bhattacharya 2006) and so it is reasonable that salinity becomes higher downstream when the flow influence has weakened and where shallower areas are present. In the idealized model, salinity averaged over time and spatially correlates with stream order number. However, this link can be modulated by the length or the width of the channels, which can vary significantly between different orders. The analysis of the Mississippi data yields similar trends between salinity and stream order, and thus supports the conclusions from the idealized model. Nevertheless, the limited number of stream orders in both the Mississippi and idealized deltas limits a fully quantitative regression and the generalization of salinity stream order relationships to other natural systems.

Our results also indicate that changes in stratification between different dynamic conditions might also be related to the channels classification. There is a shift in the PEA magnitude inside channels of the same SO number for different flow stages. When dispersion prevails (dry periods), the PEA was found to decrease with the decrease of the SO. In this case, the deeper channels of high SO are more stratified than the others. When advection is dominant (wet period), the most proximal to the river channels are well mixed with PEA becoming zero while channels of low SO order remain partially mixed.

Conclusions

We used an idealized numerical model to investigate the salinity field in a river dominated delta. We modelled salinity variations under the influence of an annual symmetric flow and determined and classified the spatial distribution of salinity during wet and dry seasons, mass balance and flushing time.

Model results indicated that salinity averaged over delta cross-sections decreases exponentially with river discharge. This relationship appears similar to the simple theoretical solution of the 1D advection-diffusion equation under steady conditions and constant diffusion and cross-sectional area.

The implementation of the same methods on salinity-flow data from the Mississippi River Delta showed a weaker exponential correlation between salinity and river discharge. Considering the deviations from the classical assumptions required (i.e. steady-state flow, constant cross-section and diffusion coefficient) and that external forcing not included in our model (e.g. waves, wind etc.) might be present, this is somewhat expected. In spite of this, our analytical expression could work as a best alternative for a first estimation of salinity values when there is lack of data. It provides the opportunity to estimate salinity levels at a certain time and location with respect to the river channel for a known river discharge. This significant outcome could be extremely useful for water management and local authorities. River diversions, dam construction, sea level rise, limited fresh water inflows and prolonged drought periods are a challenge for water supply policies.

Secondly, the Strahler-Horton stream labelling method was introduced and adapted for deltaic systems to achieve a delta channels classification based on their connectivity. A relationship was found to exist between the salinity level and the system’s bifurcation. Salinity generally increases as the stream order decreases. Channels of low connectivity (i.e. low number of junctions and nodes) are exposed to high oceanic salinity since they are the farthest from the river. The stream order number method is a scale-independent method that can be easily implemented to other real deltas. The same analysis done with observations from the Mississippi delta agreed with our model results. Therefore, the number of channel branches can be another indicator of high or low salinity in addition to the distance from the river. In the absence of field data, this outcome can be useful for an estimation of delta areas which are more prone to high salinity. Furthermore, the stream order number can be connected to the potential energy anomaly which is used as a measure of stratification. It identifies stratified areas close to the river in dry seasons and far from the river in wet seasons. It should be noted though, that these conclusions are valid only for a river dominated system. The validation of these methods applicability in cases including the impact of tides, waves and different bathymetric conditions will be the topic of a future work.

APPENDIX

Map Plots with Salinity Contours and Flow Vectors

Fig. 14

Monthly averaged salinity and flow vectors at every layer and each month. Number 1 corresponds to surface and number 4 to bottom layer. Colormap (Thyng et al.2016)

SENSITIVITY TEST ON THE NUMBER OF VERTICAL LAYERS.

We present here the results of the sensitivity test on the number of vertical sigma layers. The model was run with 4, 6, and 8 sigma layers and results are summarized into percentage increase of the top-bottom salinity difference (Fig. 13) and the impact on the potential energy anomaly averaged within channels of the same stream order (Fig. 14). The delta area remains largely unaffected both during the dry season when the largest differences are mainly observed inside the deep river inlet and during the wet season when the largest difference are observed offshore while fresh and well mixed conditions prevail in the delta (see section 3.1). Even though the number of vertical layers does change the magnitude of PEA in Fig. 14, it does not affect the qualitative dependence of PEA on stream-order.

Fig. 15

The percentage increase with respect to the simulation of 4 vertical layers in the top to bottom layer salinity differences in the case of A) six layers in the dry season B) eight layers in the dry season C) six layers in the wet season and D) eight layers in the wet season

Fig. 16

The evolution in time of the potential energy anomaly (PEA) averaged within channels of the same stream order in a simulation with A) four B) six and C) eight vertical layers