How cost-efficient is energy efficiency in buildings? A comparison of building shell efficiency and heating system change in the European building stock

Abstract

Mitigating CO₂ emissions for space heating (SH) and hot water (HW) preparation in buildings is key to reaching climate protection targets. In this context, it is important to understand meaningful balances between CO₂ reduction through thermal renovation activities and the change of heating systems. In this work, we develop cost-optimal balances for different system settings with the Invert/Opt model. This model optimises the measures applied in each building so that the system costs for SH and HW preparation are minimised under given constraints for a given country. About 500–1000 options are considered for each building. We calculate scenarios and sensitivities for all countries of EU-27, reflecting a 95% reduction in CO₂ emissions for SH and HW with a mix of direct and indirect RES technologies. These differ in the settings related to the applicability and costs of building-shell-related measures and the costs and availability of resource potentials. The results show that probably a high share of thermal renovation on total upcoming refurbishment activities until 2050 is cost-efficient to reach a 95% CO₂ reduction in the EU-27 building stocks. Assuming that up to 90% of the buildings in each EU-27 country is applicable for a thermal renovation in case a refurbishment activity is needed leads to around 4% lower system costs by 2050 (13 billion EUR/year) compared to assuming a maximum share of 35%. Energy needs are reduced on average more in older buildings than in newer buildings. Nonetheless, a combination of thermal renovation and heating system change is often the most cost-effective option to reduce system-wide CO₂ emissions also in more recent buildings. The calculations lead to cost-optimal savings in final energy demand in the range of 29–47% between 2019 and 2050. Assuming less favourable conditions for thermal renovation (high capital recovery expectations, additional technical barriers and high availability of cheap fuels) the cost-optimal level of heat savings in buildings for overall EU-27 could be suspected at around 1/3 down to 1/4 of current final energy demand.

Introduction

In December 2018, the European Parliament and the Council adopted Regulation (EU) 2018/1999 on the Governance of the Energy Union and Climate Action (EP, 2018a). The aim was to set common rules for planning, reporting and monitoring the track towards reaching the goals of the Paris Agreement. Furthermore, in Article 2 (18), the energy efficiency first principle is introduced: “‘energy efficiency first’ means taking utmost account in energy planning, and in policy and investment decisions, of alternative cost-efficient energy efficiency measures to make energy demand and energy supply more efficient, in particular by means of cost-effective end-use energy savings, demand response initiatives and more efficient conversion, transmission and distribution of energy, whilst still achieving the objectives of those decisions”. A year later, in December 2019, the European Commission launched the European Green Deal. It is a set of policy initiatives to transform the EU to carbon neutrality until 2050. In the European Green Deal presentation, the Commission already made clear that “energy efficiency must be prioritised”. Specifically for the building sector, accounting for around 40% of energy consumption, the announced ‘renovation wave’ and a recast of the Energy Performance of Buildings Directive (EPBD) aim to at least double the current renovation rates of 0.4–1.2% per year (COM, 2019). The latest version of the EPBD published in 2018 (Directive 2018/844/EU) stated that “Member States should seek a cost-efficient equilibrium between decarbonising energy supplies and reducing final energy consumption.” (EP, 2018b). In summary, the EU has agreed to emphasise energy efficiency and integrate it into all energy-related considerations, seeking at the same time cost-efficient balances between efficiency increase and decarbonised supply. But how do such balances look like in the building sector?

Obviously, finding cost-optimal equilibria between efficiency increase and decarbonised supply is highly relevant for identifying feasible pathways towards decarbonisation. In the context of decarbonising energy demand in buildings, the adoption of the recast of the EPBD in 2010 (Directive 2010/31/EU) marked a milestone in increasing the efforts to find concrete answers to this search. In (10), the Directive 2010/31/EU requires “Member States to set minimum requirements for the energy performance of buildings …”, “… [t]hose requirements should be set with a view to achieving the cost-optimal balance between the investments involved and the energy costs saved throughout the lifecycle of the building.” (EP, 2010). This triggered a remarkable number of studies and analyses to identify cost-optimal levels of energy savings in European buildings.

On the one hand, as required by the EPBD, Member States (MSs) had to define minimum requirements for the energy performance of buildings based on cost-optimality calculations. With the COMMISSION DELEGATED REGULATION (EU) No 244/2012 (COM, 2012a) and the accompanying guidelines to that regulation (COM, 2012b), the COM provided a framework for these analyses. Based on these, the MSs performed cost optimality calculations at national or regional levels and delivered them to the COM by 2013. Evaluations of this first round of cost-optimality calculations by the MSs showed remarkable gaps between the calculated cost-optimal levels for different building types and the minimum performance requirements defined by the national standards (Boermans et al., 2015). In most cases, they found that cost-optimal levels lie below the requirements, differing between the type of building and the type of action (new construction vs renovation). The evaluation of (Zirngibl & Bendžalová, 2015) finds that not all MSs have a complete set of calculation methods, mainly due to missing coverage of certain building categories or building stages, most often related to non-residential renovated buildings. A profound study by Paolo Zangheri et al. (2018) proposes an additional method to calculate cost-optimal levels of building renovation consistent with the framework set out by the EU (COM, 2012a). This method should improve shortcomings identified in the first round of national cost-optimality calculations and in previous analyses applying the European comparative approach proposed in the EPBD. With the proposed method, Zangheri et al. (2018) calculate primary energy savings and related costs for the renovation of 4 reference building types (2 residential and 2 non-residential) built between the 1960s and 1970s in 10 different climates in Europe. Various measures were considered for renovating the building envelope as well as for changing the energy supply system. They found a very relevant energy saving potential for all analysed cost-optimal targets between 36 and 88% in terms of net primary energy. Also, they conclude that the compilation of consistent and reliable data for the costs of renovation activities is the most critical step in such an analysis.

Apart from Zangheri et al. (2018), numerous studies were performed to identify cost-optimal levels of renovation of single buildings or building archetypes. Some of these studies analyse individual real existing buildings: an apartment building in Bilbao (Iturriaga et al., 2018); a multi-family building from 1961 in Lingköping, Sweden (La Fleur et al., 2019); a single-family building in the region of Rhone-Alpes (Ferrara et al., 2015); a public administration building in Aachen (Kumbaroğlu & Madlener, 2012); a social housing building in Italy (Carpino et al., 2020). Other studies, like also Zangheri et al. (2018), focus on selected typical or reference buildings: Corrado et al. (2014) on apartment buildings in Italy built between 1946 and 1960, Kuusk et al. (2014) on brick apartment buildings in Estonia built between 1960 and 1990, Niemelä et al. (2017) on large panel apartment buildings in Finland built between 1960 and 1990, and Sağlam et al. (2017) who focus on high-rise apartment blocks in Turkey. All these studies, analysing single or typical buildings, use a detailed modelling framework to represent the building physics and the related energy need and demand. Often, a remarkable number of refurbishment and heating system change options are also considered. At the same time, taking into account resource restrictions as well as interactions in the entire energy system is not possible at this analysis level. Therefore, it is not possible to upscale the results of the cost-optimality calculations for single buildings or building types to the national or EU level to understand cost-optimal saving levels.

Also, studies were performed at the city or regional level to identify cost-optimal levels of heat savings in buildings.

Ben Amer-Allam et al. (2017) and Büchele et al. (2019) study how to identify cost-optimal mixes between district heating, individual heating and heat savings for the municipality of Helsingor in Denmark and the city of Brasov in Romania, respectively. Both analyses integrate the area’s building stock via archetype buildings and related heat-saving measures, distinguishing between areas of the city that are more or less feasible for DH. Cost-optimal mixes of different levels of heat savings and different heat supply technologies are then identified for each area more or less feasible for DH. For Helsingor, cost-optimal savings are calculated to be 20–39%, mainly depending on the economic perspective (simple socio-economic vs private-economic) and less on the assumed technology mix in the DH system. Büchele et al. (2019) calculate a cost-optimal level of heat savings in Brasov to 64% over the entire stock until 2050, which is equal to the overall identified technical heat-saving potential with very ambitious measures. This is generally explained by relatively low renovation costs compared to the heat supply costs, as well as the analysis method. In the studies of Prohaska et al. (2020), Simon et al. (2020) and Martinez et al. (2020), future scenarios of heat demand and supply with the aim of nearly full decarbonisation were developed for the cities of Frankfurt, Bistrita and San Sebastian. The building stocks of the cities were considered via 70 building archetypes geolocated over the cities. Various heat-saving measures were developed for each archetype. Scenarios for the entire city were derived via sequential analysis of heat savings, DH expansion, DH supply and individual supply, and combining meaningful variations of these. The calculated scenarios indicate economically interesting heat-saving levels between 24% (San Sebastian), 36% (Bistrita) and 53% (Frankfurt). Also, the studies clearly show that the economically interesting heat-saving level is remarkably influenced by the assumptions on the availability of local resources for carbon–neutral heat supply. Although these studies show a range of relative heat savings that seem to be cost-efficient at city level, it is again not possible to upscale the results of these studies to the national nor EU level.

Inspired by the German energy transition and the concern about the cost of future energy systems solely based on renewable energy, Henning and Palzer (2014) developed the REMod-D model for optimising energy systems at the national level. The model is based on an hourly energy balance approach for both the electricity and the heating sector and applies a mathematical–numerical optimiser to identify system configurations with minimal overall annual costs. Besides various heat and electricity supply options, building retrofit measures are integrated into the model via one cost-potential curve for savings in all buildings. Palzer and Henning (2014) present an application of the model by calculating three main scenarios and various sensitivity runs for Germany’s 100% renewable heat and electricity systems in 2050. They calculate a cost-optimal saving level of countrywide heat demand between 2010 and 2050 to be 31.8%. A variation of the assumed costs for heat savings shows that the total system costs do increase much less in relative terms compared to the increased saving costs. However, the exploitation of technical resource potentials strongly increases with increased saving costs. Thus, they conclude that ambitious levels of heat savings in building retrofitting will be needed to reach 100% renewable energy in heat and electricity use, considering that full exploitation of technical resource potentials will most probably not be possible.

Zvingilaite and Balyk (2014) analyse feasible levels of heat savings in future 100% renewable heat and power systems in Denmark at different shares of district heating using the optimisation model Balmorel. Heat savings are integrated into the model via cost-potential curves for different types of measures on the wall, floor, roof, windows and ventilation systems with heat recovery over the entire building stock. Scenarios are calculated for the year 2050 with differing district heating expansion and resource availability. The calculations result in cost-optimal saving levels in the range of 12–17%, depending on the scenario. Although the cost-optimal savings are relatively low compared to other studies discussed before, a remarkable effect of reduced resource potentials is visible. Heat savings are mainly achieved through windows upgrade and roof insulation in scenarios with lower resource availability, but scenarios resulting in higher optimal saving levels also consider ventilation with heat recovery. Zvingilaite & Balyk, 2014) also show that heat savings are more cost-effective in buildings with individual heat supply than in buildings connected to district heating and conclude that it is important to consider heat generation systems and technologies in assessing heat-saving options instead of using one assumed future energy price.

The Heat Roadmap Europe (HRE) initiative studied cost-optimal levels of heat savings in buildings at transnational and European levels (Mathiesen et al., 2019). The third of four HRE studies developed low-carbon heating and cooling strategies for five MSs, using the energy system model EnergyPLAN. Costs and effects of heat savings in buildings were integrated into the analyses based on cost-potential curves developed for the entire building stocks. Different levels of demand reduction were then integrated into the EnergyPLAN calculations, and the costs for heat savings were taken into account in calculating overall system costs. Based on the developed data and calculations, Hansen et al. (2016) tried to understand cost-optimal heat saving levels at the national level, including differences between countries. They find heat savings of 30–50% of projected heat demands in 2050, and supplying the remaining heat demand with sustainable heat sources could avoid overinvestments in the heating demand and supply systems. They identify factors largely influencing the cost-optimal heat saving levels to be the current state of the building stock, the overall level of specific heat demands, the heat supply costs and the technical heat saving potential up to 2050. The fourth HRE study developed integrated low-carbon heating and cooling strategies for 14 MSs, again analysing different levels of heat savings and supply structures, and again using the same modelling approach as in the HRE third study, although using different data for calculating costs and potentials for heat savings. The calculations confirm the findings of HRE 3: cost-optimal levels lie in the range of 30–50% heat savings by 2050, and differences between the countries are remarkable. Also, due to high shares of district heating of 30–50% leading to the lowest overall system costs in the analyses with EnergyPLAN, they conclude that there is likely a synergetic effect between heat savings and district heating in the residential sector (Mathiesen et al., 2019).

To improve the information basis for designing policies targeting the decarbonisation of space and water heating in Europe, the EU COM ordered a study to collect the status-quo of consumption and technology data as well as the regulatory framework (EC DG-ENER et al., 2022). Furthermore, different technology pathways for fully decarbonising the EU space and water heating were modelled to understand long-term perspectives and related costs. To derive the technology pathway scenarios two models were linked, the Enertile model of Fraunhofer ISI for calculating the generation of electricity, liquid and gaseous e-fuels and district heating from renewable sources, and the Invert model from TU Wien and e-think to calculate cost-optimal balances between thermal renovation and heating system change for decarbonising space and water heating in buildings. With this model setting 6 technology pathway scenarios were calculated assuming different constraints for the usability of technologies and resources: direct RES-H (focusing on individual supply options), electrification, e-fuels, hydrogen, district heating and one so-called ‘best-case’ scenario. Due to relatively small differences in the resulting system and transaction costs between the different scenarios, the authors concluded that the costs do not deliver a clear criterion for deciding which technology pathway should be followed. At the same time, several results were similar in the different scenarios and indicate decarbonisation options that should be strongly considered: a high level of thermal building renovation, a high diffusion of heat pumps and a high diffusion of district heating in suitable areas. Overall, cost-efficient savings in final energy demand between 2017 and 2050 of 45–47% were calculated for the scenarios reaching a 95% reduction in CO₂ emissions.

In summary, cost-optimal heat savings levels at national and EU-wide level seem to be in the range of 30–50% and depend largely on the current state of the building(s) (stocks), the assumed resource availability and prices as well as the underlying costs and characteristics of renovation measures. However, it is unclear how far different non-economic barriers and drivers for thermal renovation affect cost-optimal levels of heat savings versus low-carbon heat supply and how sensitive cost-optimal heat saving levels are in relation to different cost levels of renovation measures and resource prices and availabilities. Therefore, this analysis aims to quantify cost-optimal levels of heat savings versus low-carbon heat supply in the EU-27 building stock under differing assumptions related to possible limitations of the share of thermal renovation on total refurbishment activities, the length of renovation cycles, the potential level of renovation costs, assumptions on additional non-economic barriers to thermal renovation as well as to the price and availability of gaseous and liquid low-carbon fuels. A pre-condition is a 95% reduction in CO₂ emissions between 2019 and 2050. The analysis should be done with a high level of detail on the EU building stock and potential differences in decision options. For this purpose, a newly developed optimisation variant of the well-established building stock model Invert is used. This considers all residential and service buildings in the EU-27, a broad set of passive (refurbishment) and active (heating system change) measures to decrease CO₂ emissions and takes into account rebound effect and user behaviour in the calculation of energy needs as well as resource restrictions for low-carbon heat supply options.

Methodology and input data

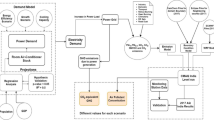
For the analysis in this work, we use the optimisation model Invert/Opt. The Invert/Opt model is a recent development to add an optimisation model to the Invert model family.¹ It applies a mixed-integer linear programming (MILP) algorithm for finding cost-optimal combinations of renovation and supply options under given constraints. In addition to Invert/Opt, the Invert model family also consists of Invert/EE-Lab, applying a simulation approach, Invert/Acc applying an accounting approach and Invert/CC deriving energy saving (and supply) cost curves. All Invert models are based on a detailed representation of the existing building stocks at the national (or local) level via building archetypes, various potential options for renovation and available heat supply technologies for each archetype. All models access the same input databases when calculating for the same region. In the further description, we call them collectively ‘Invert database’. The following Fig. 1 shows an overview of the data input and output as well as the calculation logic of the Invert/Opt model.

Fig. 1

Method and input data of the Invert/Opt model

In the following subsections, we first describe the databases of existing buildings stocks, heating and hot water supply technologies, and building refurbishment options. This is followed by a presentation of the objective function and the applied constraints in the Invert/Opt model. Finally, the assumptions on energy carrier potentials and prices and the settings of the calculated scenarios are described.

The databases of building stocks, heat supply technologies and refurbishment options

The Invert/Opt model builds on three input databases for each analysed country: a database of the existing building stocks, a database of heating and hot water supply technologies, and a database of refurbishment options. In the database of the existing buildings, the building stocks are described via different typical buildings. The following properties distinguish these typical buildings: geometry and physical properties of the building shell (u-values and thermal capacity of different components, share and orientation of windows, shading installations), type of use and related occupancy profiles, construction period, region of location relevant for climate and energy carrier availability, status and period of the last renovation if already renovated, and installed heating system together with the installation period. In the description of this work, we apply the following nomenclature related to the typical buildings: a building archetype includes all stated properties apart from the heating system. We call a building archetype with a certain heating system a building segment. Depending on the level of detail of available data in the different countries, we distinguish between 18,660 and 296,529 different building segments for the analysed countries.

The Invert database on existing building stocks was compiled over the last decade in the course of numerous projects. An important data source for residential buildings is the Tabula/Episcope building stock database for residential buildings, described e.g. in Loga et al. (2016). Physical properties of the buildings like thermal capacity, infiltration, natural ventilation as well as occupancy profiles were taken from EN ISO 13790:2008 (CEN, 2008). Furthermore, national and EU-wide statistical data and publications were used to define number of buildings, gross floor area and u-values for different building types and construction periods, as well as demand for energy carriers for space heating and hot water. ENTRANZE (2014), ZEBRA2020 (2015) and CommONEnergy (2017) offer a representation of the data contained in the Invert database on existing building stocks; EUROSTAT (2022a) and EUROSTAT (2022b) were used to calibrate the energy demand in the base year 2019 used in this study. Additional details and data are presented in Müller (2015).

In the Invert database of heating and hot water supply technologies, we compile data on efficiency, investment costs, operation and maintenance (O&M) costs, energy carriers used as well as lifetime of different technologies, including photovoltaic (PV) systems for on-site electricity generation. In the database, we distinguish these data between the different countries, take into account technological learning in the development of efficiency and investment costs, and apply economies of scale for different system sizes. The main data sources for heating and hot water supply technologies in the Invert database are Danish Technology Catalogue (DTC) (DEA, 2021) and other national data sources for selected countries. Data from the DTC were recalculated for other countries using the construction cost indices.

Finally, the Invert database of refurbishment options contains data on various refurbishment activities tailored to each building archetype in the building stock database. Two types of refurbishment activities are defined for each building archetype: a maintenance activity and several thermal renovation activities. Maintenance increases the lifetime of the building components but does not decrease the heat demand of the buildings. Thermal renovation instead increases the lifetime of the building components and reduces the demand for space heating in the buildings. For each building archetype, several thermal renovation packages are contained in the database consisting of combinations of single measures like the change of windows, insulation of exterior walls, roofs, attics or basements, as well as ventilation systems with heat recovery. These packages reflect the cheapest combination of single measures for reaching a predefined saving target. A more detailed description of the applied method for deriving these thermal renovation packages, as well as the data sources used for the costs of the refurbishment options, is provided in Hummel et al. (2020). For each refurbishment activity, the database contains investment costs and resulting u-values of the different building components.

The optimisation model Invert/Opt

Calculation of energy needs for space heating and hot water generation

Energy needs and delivered energy for space heating and hot water generation are calculated using the described databases of building stocks, supply technologies and refurbishment options, together with data on climate (monthly mean temperatures, solar irradiation) and user behaviour (time of use, indoor set temperatures). Calculations are performed according to the quasi-steady-state monthly energy balancing method defined in EN ISO 13790:2008 (CEN, 2008), applying a single-zone model. In comparison with more detailed methods (e.g. dynamic multi-zone models), the Invert model leads to sufficiently accurate results for a wide range of buildings and climate regions (Zangheri et al., 2014).

Climate data are taken from the EnergyPlus Weather Converter V7, with the exception of Spain and Italy, where we used the climate of important cities: Italy and Spain have been split into three climate zones (Palermo, Rome and Milan as well as Sevilla, Barcelona and Madrid). Considering that the climate data retrieved from the EnergyPlus Weather Converter represent the long-term climate conditions, the current and future climate has been adopted based on the historical development of the national heating degree days (HDD) as provided by EUROSTAT (2021) and the extrapolation of the observed trend. The resulting reduction in annual HDD between 2020 and 2050 ranges from ~ 20% in warmer countries such as Cyprus, ~ 10% in Spain, ~ 7.5% in Germany and about 5% in Finland. While HDD and climate data change over time to represent climate change in the analysis, potential effects of social and demographic change on e.g. the occupancy profiles in the different buildings are not considered. Various behavioural aspects supplement the calculation procedure to account for the observed differences between measured energy consumption and demand derived according to the standard calculation. Several factors affect the indoor set temperature and the heated area in a building, like the HDD, the type of heating system, the running costs and the household income. These factors not only allow for considering the observed difference between measured consumption and calculated demand, but also allow for integrating the rebound effect after thermal renovation as well as differences in thermal comfort due to income, selected heating system and energy carrier prices. Müller (2015) describes further details on these calculations of the energy needs and the final energy demand.

Calculation of delivered energy, costs and emissions for possible options

In the model, the resulting energy demand parameters, costs and emissions of all possible combinations of supply systems and refurbishment options in the different building segments of the analysed countries are calculated. About 500–1000 options for each building segment are considered: 4 (+ 1) refurbishment options (one maintenance, three thermal renovation options and no activity), 15–20 heating systems, 2 (+ 1) solar thermal systems (6 or 15 m² collector area per household,² no solar thermal system) and 2 (+ 1) PV systems (40 or 90% of solar suitable roof area, no PV system).

To calculate the delivered energy for most technologies, the system efficiency together with a system-specific service factor is applied, the latter representing different shares of floor area being heated for different types of technologies (single vs. central systems). For solar thermal systems, a defined yearly heat generation per square meter of collector area is used. In case of PV systems, the calculation is more complex. Generally, the use of electricity generated by PV to supply electricity demand from appliances in the buildings is prioritized in the model. Hourly profiles of solar irradiation and electricity load for appliances are used to calculate the amount of electricity potentially available for heating or for export to the grid. Standard load profiles from ENB (2021) for different types of buildings are used as a basis and superimposed by an hourly oscillation with the factors 1.2/1.3/2 and 0.83/0.76/0.5 depending on the type of building. If the on-site PV production in any given hour exceeds the electricity load, the model chooses whether to use the electricity for heating purposes (direct electric resistance heating or as electricity input for heat pumps) or to feed into the grid. The decision parameters are the feed-in tariffs as compared to the price of the energy carrier used to produce heat (along with the efficiency of the boiler) and the daily heat demand for domestic hot water preparation and space heating.

The share of buildings in each building segment implementing a refurbishment option and/or a replacement of the heating system between the start year and the target year of the analysis is endogenously determined by the model. This is based on distributions of moments of construction, past renovation and heating system installation, together with Weibull distributions of the lifetime of the components. The lifetime of the building shell components is defined between 45 and 60 years depending on the age of the buildings (old buildings usually show longer refurbishment cycles). It is assumed that the lifetimes are the same in all countries. In case a building segment implements a refurbishment activity, all building shell components are treated, whether with a thermal renovation or a maintenance activity. Thus, after implementing a refurbishment activity, all components have the same moment of activity and lifetime (see also Hummel et al., 2020). The calculated properties of all possible options in all building segments together with several restrictions and constraints form the input for the upcoming optimisation part of the model.

Identification of activities in all buildings to reach targets at given constraints

For each country, the optimisation module of Invert/Opt identifies the combination of refurbishment option k and supply system change j in each building segment i that leads to the lowest overall system costs at a given time in the future starting from the currently existing status:

$$\begin{array}{c}min\sum_i\sum_{j,k}\left(C_{supply,j,i}+C_{refurb,k,i}\right)\\C_{supply,j,i}=C_{invest,j,i}\cdot{CRF}_j+C_{O\&M,j,i}+C_{energy,j,i}\\C_{refurb,k,i}=C_{invest,k,i}\cdot{CRF}_k\end{array}$$

The system costs C are calculated as annualised investment costs in supply systems C_invest,j,i and refurbishment options C_refurb,k,i using respective capital recovery factors (CRF) plus yearly O&M and energy costs for the supply systems. In each building segment hereby, various combinations of supply system changes and refurbishment options might be contained in the optimal solution. This is due to the considered constraints. In the following, we describe these constraints according to the level at which they are applied in the model. The share of buildings hereby always refers to share in terms of gross floor area (GFA), not of number of buildings. As described before, the model optimises all investment decisions taking place between the start year and the end year of the analysis period. Therefore, also the defined constraints apply for the entire analysis period.

• Constraints at the level of building segments:

  • The share of buildings that install a solar thermal system must be below a defined threshold.

  • The share of buildings that install a PV system must be below a defined threshold.

  • The share of buildings that install a solar thermal system, a PV system or both must be below a defined threshold.

  • The share of buildings using a certain energy carrier must be between defined minimum and maximum values. This is defined for each energy carrier in each building segment and reflects overall energy carrier potentials on the one hand and the inertia of changing from certain energy carriers to others like for district heating or gas systems on the other hand.

  • The share of buildings implementing a maintenance action must be between defined minimum and maximum values. The minimum share of maintenance reflects that not all constraints to thermal renovation are explicitly included in the model, like construction details leading to a remarkable increase in renovation costs making it uneconomic, even if the model considers thermal renovation the cheapest option. On the other hand, the maximum share of maintenance reflects the situation where thermal renovation measures are implemented, even though it would be the cheapest option to perform maintenance on the building shell, which might be the case for people willing to save energy.

• Constraints at the level of energy carrier (groups):

  • For several energy carriers, a cost-potential curve is implemented in the model, i.e. the absolute amounts of the different energy carriers available at different prices are set in the input data. This applies to all biogenic energy carriers.

  • For each energy carrier, a diffusion restriction is implemented in the model, limiting the yearly increase in the use of the energy carrier.

  • For similar energy carriers, groups are defined: biomass, oil, gas, coal, district heating and electricity. The share of buildings using energy carriers of a certain group must be between defined minimum and maximum values.

• Constraints at the country level:

  • The overall CO₂ emissions of heat and hot water supply in all buildings in a country must be below a defined threshold. This threshold is defined in two ways: (1) in terms of relative savings compared to the current state and (2) in terms of CO₂ emissions per GFA. In case the relative savings cannot be reached with the given technology and renovation options, the definition in terms of emissions per GFA is applied by the model.

  • The share of buildings implementing a maintenance action must be between defined minimum and maximum values. Similar to the minimum and maximum shares of maintenance defined at the building segment level, these constraints at the country level reflect constraints to thermal renovation or maintenance that are not explicitly integrated into the model.

Energy carrier potentials and prices

Important inputs to the model and the related scenarios are the settings for the energy carriers to be used in the buildings. This concerns the availability of resource potentials and the related prices of energy carriers both for decentral and grid-associated utilisation. In the following sections, the general approach to deriving available resource potentials and related prices is described, and then additional details for specific energy carriers are presented.

General approach

With regard to the resource potentials, different constraints are implemented in the model. First, the maximum potentials of heated gross floor area that can be supplied by a certain energy carrier or a certain technology are defined for each country. Further on, these are called saturation constraints. On the one hand, they reflect technical restrictions like the fact that a gas network must be available for the widespread use of gaseous fuels or that corresponding heat densities must be available for the efficient and competitive use of district heating. On the other hand, they reflect socio-economic restrictions like the limited acceptance of biomass-based decentral boilers in urban areas due to local emissions. To define the saturation constraints for each energy carrier in each country, we first split the building stock in each country into a rural and an urban part of the stock using Eurostat statistics. The use of biomass technologies in urban buildings is then extremely restricted, while especially in small rural buildings these technologies are nearly unrestricted. Air-source heat pumps in rural areas are nearly not restricted in the model; in urban areas they are. Ground-source heat pumps are extremely restricted especially in existing urban buildings. More details on setting the restrictions are described in Fleiter et al. (2016). To define the maximum shares of district heating in each country, we analysed data regarding heat demand densities (Müller et al., 2019), defined a maximum expansion velocity and allocated the resulting gross floor areas to building types according to their shares in rural and urban areas. For setting the maximum shares of heated gross floor area potentially supplied with natural gas, we analysed the locations of the transmission pipelines and the geographic distribution of the gross floor areas. Assuming a decreasing probability of an existing gas distribution grid with increasing distance to the transmission grid as well as full availability in large cities leads to maximum shares of heated gross floor area with gas systems (Schremmer et al., 2018). The resulting maximum shares of heated gross floor area, where a certain space heating technology can be applied, are shown in Table 1.

Table 1 Maximum shares of heated gross floor area where a certain space heating technology can be applied—saturation constraints

While the saturation constraints reflect the maximum potentials for given technical and socio-economic restrictions, additional limitations might exist due to policy measures focusing on certain technologies. Thus, on top of the saturation constraints, we integrate diffusion constraints specific for each energy carrier or technology to reflect a general focus on certain technology pathways. In the scenarios presented in this work, these diffusion constraints are set the same for all countries and focus on the direct use of renewable energy in the buildings: solar thermal, PV and direct use of biomass resources in the buildings are not further restricted, for gas-based technologies (boilers, CHPs and heat pumps), electricity-based technologies (heat pumps and direct electric heaters) and for district heating the diffusion constraint until 2050 is set to 50% of the saturation constraint, and for oil-based boilers, the diffusion constraint is set to 25%. In addition, an absolute resource restriction is defined at the country level for decentral biomass utilisation. The following section describes more details of this restriction.

The prices for most energy carriers are calculated with the Enertile model,³ developed and run by Fraunhofer ISI. The model determines the optimal portfolio and its dispatch for the supply of electricity, district heat, hydrogen and e-fuels to reach the lowest system costs. The demand is hereby defined for each hour of a certain year for each country, and the resource and generation potentials are partly defined at a higher spatial resolution, whether in the form of raster data for wind and solar technologies or point data for larger plants. While the price development for fossil fuels is an input to the model, the prices for hydrogen, synthetic methane, bio-liquids, e-liquids, electricity and district heat are output from the model. These outputs are then used in the Invert/Opt model for the calculation of the scenarios presented in this paper. Hereby, Enertile yields wholesale prices of these energy carriers and Invert/Opt calculations are based on retail prices. To convert wholesale prices to retail prices, company markup, taxes (energy and VAT⁴) and grid charges must be added. While the company markup and the taxes are assumed to stay constant for each country’s residential and service sectors, grid charges are assumed to change due to remarkable changes in the grid infrastructures. The assumptions related to these changes are described in the next section.

The fossil fuel price development is based on the IEA sustainable development scenario (SDS) in the World Energy Outlook 2019 (IEA, 2019). In this scenario, crude oil, natural gas and steam coal prices remain roughly at today’s level with a slight decline. However, for the supply of electricity, district heat (in Enertile) and decentral use in buildings (in Invert/Opt), only minor amounts of fossil gas, oil and coal remain in the supply mixes. Exogenous assumptions were made for the share of different components in the gaseous and liquid fuels directly used in the buildings. Details are described in the next section. In the calculations with Enertile, a limited carbon budget is applied. It reflects nearly full decarbonisation of electricity and district heating supply in 2050 with a total budget of 5 Mt CO₂ for the sum of emissions of these two sectors from all EU countries. Compared to the emissions in these sectors in 1990 of 1500 Mt CO₂, this reflects a 99.67% reduction.

In the calculation of optimal portfolios and dispatch for hydrogen, synthetic methane, e-liquids, electricity and district heat, the demand for these energy carriers in buildings, industry and transport is a basic input. Enertile hereby considers the demand for these energy carriers from all sectors. In the current analysis, the demand for these energy carriers was taken into account in two different ways: (1) The demand from space heating and hot water generation in buildings calculated by Invert/Opt is used as direct input to the Enertile calculations. Since Invert/Opt, on the other hand, uses the energy carrier prices calculated by Enertile, an iterative calculation procedure between both models was applied. (2) The demand for these energy carriers from all other sectors is defined as exogenous input to the Enertile model. Hereby, the EU-wide demand for these energy carriers in 2050 from the 1.5TECH scenario from the European Commission (COM, 2018) was used and broken down to country level and back to 2030 and 2040 using the national distributions and developments over time as calculated in the SET-Nav pathway ‘Diversification’ (Hartner et al., 2019; Sensfuß et al., 2019). This leads to an EU-wide energy demand from all sectors except buildings and district heating of 4144 TWh electricity (whereof 15% results from transport purposes), 473 TWh e-liquids, 266 TWh synthetic methane and 707 TWh hydrogen. With the Enertile model, it is furthermore assumed that carbon capture and storage (CCS) is not available for fossil-fuel-based electricity generation.

As explained, the Enertile model optimises the generation of electricity, hydrogen, synthetic methane, e-liquids and district heating based on available resource potentials, demand for these energy carriers in different sectors as well as the settings described before. Clearly, the resulting wholesale prices for the stated energy carriers depend on the demand for these energy carriers in the different sectors. Within the study ‘Renewable Space Heating under the Revised Renewable Energy Directive’ for the European Commission, various technology pathway scenarios have been analysed (EC DG-ENER et al., 2022).⁵ For the analyses within this paper, the diversified technology pathway scenario has been selected as the base scenario (in the report called ‘Direct RES-H’). In this scenario, no strong preference of any technology pathway was assumed, rather a diverse mix of different technology options in the buildings and district heating portfolios. More details on the method and the assumptions in the Enertile model can be found in the final report of the respective study (EC DG-ENER et al., 2022).

Details for selected energy carriers

Biomass is a restricted resource, heavily demanded as energy and material in various sectors. As we do not explicitly model the competition between the different potential biomass uses, we consider an absolute potential restriction for solid, gaseous and liquid biomass resources to be used for space heating and hot water generation. To define the potentials of solid biomass resources for decentral use, we orient on ongoing discussions and statements from the EU Commission targeting a reduction of overall biomass use for heating of buildings in the EU of around 10%. To define resource potentials at national levels, we apply the following simplified approach: the share of solid biomass on the final energy demand for space heating and hot water generation in buildings in a country can increase up to 15 percentage points compared to the base year if the energy demand at the same time decreases by 50%. In addition, the maximum share is defined as 33%.⁶ In total, this leads to a resource potential for decentral solid biomass utilisation of 468 TWh for all EU-27 countries corresponding to 91% of the amount used in 2019, i.e. a 9% reduction compared to current levels (see Table 2). This approach is a remarkable simplification, at the same time it is transparent and considers that solid biomass is tradeable and does not necessarily need to be consumed in the country of origin. The prices for the solid biomass energy carriers, wood logs, wood chips and pellets we assume to stay at today’s levels.

Table 2 Resource restriction for decentral biomass utilisation

Gaseous fuels in buildings are mainly consumed in connection with a gas distribution grid. For the gas distributed in the grids, the following composition is defined: 3% fossil natural gas, 10% synthetic methane, 10% hydrogen and the rest biomethane (see also Table 3). The average composition of liquid fuels is defined as 5% fossil heating oil, 10% e-liquids and 85% bio-oil. These assumptions are mainly driven by CO₂-reduction targets, technical limitations for hydrogen in distribution grids and estimated potentials as well as generation costs for synthetic methane and bio-oil. Nuffel et al. (2020) estimate the overall technical biomethane potential from different feedstocks in 2050 for each country of the EU. According to Peters et al. (2020), which developed a “decarbonisation pathway towards an optimal role for gas in a net-zero emissions energy system” for the EU, roughly 19% of the entire biomethane could be used in buildings. To set the potential restrictions for biomethane and bio-oil in this analysis, we take the identified technical biomethane potentials for buildings and distribute them to biomethane and bio-oil, applying the following logic: the same feedstocks can be used to either produce biomethane or bio-oil; the production of bio-oil is around 20% less efficient than the production of biomethane; Thus, correspondingly more resources are needed for bio-oil production; the potential is allocated to biomethane as well as to bio-oil according to areas where a gas grid is available and where no gas grid is available (see Table 1) hereby allocating twice as much to gas regions as to non-gas regions. This logic, together with the presented assumptions of the shares of different components in the gas and oil mixes, determines the upper limit of using gaseous and liquid fuels for space heating and hot water generation in buildings in different countries (see Table 2).

Table 3 Whole sale prices for electricity and gas mix in the distribution grid in 2050 in EUR₂₀₁₉/MWh applied in the modelling (see also EC DG-ENER et al., 2022)

As written before, the wholesale prices for synthetic methane and for hydrogen are calculated with the Enertile model and the wholesale price for natural gas and fossil heating oil is taken from the IEA (2019) SDS. For biomethane, we use production, upgrade and injection costs for the different countries as stated in Nuffel et al. (2020). We assume that the price for bio-oil is 25% higher than the price for biomethane, and the price for e-liquids is 10% above synthetic methane. The gas grid charge is assumed to increase with a decreasing gas consumption: a third of the price scales indirectly proportionally to the decrease rate. On top of that, a 5% increase of the grid charge is added, assuming additional costs for parallel transport infrastructure, one for methane and one for hydrogen. Overall, this leads to a remarkable increase in gas prices compared to the current levels ranging between 7 and 209% in the different countries with an EU-27 average (and median) of 119%.

As described in ‘General approach’ section, the saturation constraints for district heat are oriented on an analysis of heat demand densities in the different countries, and the diffusion constraint is set to 50%. The latter reflects a low level of accepted heat distribution costs. As also already described in ‘General approach’ section, the wholesale prices for district heat are calculated with Enertile. Hereby, it is assumed that large shares of DH are generated out of solar thermal and geothermal energy. To determine the retail prices for district heat in 2050, we assume that the difference between current levels and 2050 derives from differences in the wholesale prices times a factor of 1.2 plus VAT. Since no consistent information on current wholesale prices for district heating is available, we use the difference in modelled wholesale prices for 2030 and 2050 and apply this to current retail prices for district heat in the different countries in Werner (2016). For retail electricity prices, we apply the same approach with the only difference that current wholesale prices are used since they are publicly available. The wholesale prices for electricity (hourly price weighted with the hourly heat demand in buildings) as well as for the gas mix in the distribution grid together with its four components are presented in Table 3, and the retail prices for the different energy carriers finally applied in the calculations are shown in Tables 4. Figure 2 then shows a decomposition of the retail prices for gaseous fuels in the distribution grid for 2019, the default setting for 2050 according to the description before as well as for a low gas price sensitivity for 2050. In the low gas and liquid price sensitivity, we assume a wholesale gas price of 55 EUR/MWh in all countries. The decomposition shows the assumed transmission and distribution grid fees, the energy taxes and the VAT, as well as a mark-up reflecting the not explainable residuum between the before mentioned components.

Table 4 Retail prices for energy carriers in 2050 in EUR₂₀₁₉/MWh applied in the modelling

Fig. 2

Decomposition of the retail prices for gaseous fuel in the distribution grid for 2017, 2050 and 2050-low price (lp) sensitivity for the analysed countries

Several potential restrictions are applied in the modelling for solar thermal and PV. First, the share of buildings that can install a solar thermal or PV system is restricted in the form of saturation constraints, as shown in Table 1. Hereby, higher shares are considered for southern countries and lower shares for northern countries, reflecting barriers or drivers not included in costs or radiation. A second restriction considers that only a certain share of the roof can be used to install solar thermal or PV systems. Hereby, we assume that 40% of the horizontal projection of the roof of an individual building is usable in case either solar thermal or PV is installed and that 60% is usable in case both technologies are installed on the same building.

Scenario and sensitivity settings

In this work, four different scenarios as well as seven sensitivity runs are presented. In all calculations, the direct CO₂ emissions from the supply of space heating and hot water in the buildings of each country must be reduced by 95% for the period between 2019 (the start year of the calculations) and 2050. Biogenic resources are hereby assumed to be carbon neutral.

The four scenarios only differ in their settings on three parameters related to refurbishment activities: the defined minimum and maximum share of maintenance on all refurbishment activities (a) in the entire building stock of a country, (b) in individual building segments in a country and (c) the average length of refurbishment cycles of building shell elements. The refurbishment cycles in Invert/Opt are hereby endogenously calculated based on distributions of moment of construction or past renovation using Weibull distributions of the lifetime of the components (see also ‘Calculation of delivered energy, costs and emissions for possible options’ section). In a first scenario (‘Diversified’) we define low to medium shares of maintenance on total refurbishment activities in the entire stock of the countries (20–50%). Assuming an average length of refurbishment cycles of 45 years and a share of 50% of maintenance on total refurbishment activities (defined maximum for this scenario) leads to around 1.1% yearly thermal renovation rate. According to EC DG-ENER et al. (2019), this, on average, reflects the current situation in Europe. In a second scenario (‘Low efficiency’), we define medium to high shares of maintenance on total refurbishment activities (65–90%). This reflects a maximum yearly thermal renovation rate of 0.77% at country level, which is on the lower end of what is currently observed in EU-27 countries. At individual building segments, level shares of 25 to 100% of maintenance on total refurbishment activities are possible, i.e. if thermal renovation is not at all economically feasible in a building segment, no buildings perform thermal renovation, and even in segments with high economic feasibility, at least 25% implement a maintenance activity. This reflect high barriers against thermal renovation. In a third scenario (‘Low restrictions’), we define a broad range in these parameters as being possible. In a fourth scenario, these low restrictions are kept, and the length of refurbishment cycles is reduced (‘Increased renovation’). This reflects an increase in refurbishment activities over the scenario period. Table 5 shows the defined settings for the different scenarios.

Table 5 Differences in the settings for the calculated scenarios

The scenarios are calculated with a 2% interest rate, following the assumption that the current low-interest rate in the Euro area will continue for a longer period and with a depreciation time of 30 years for refurbishment activities and 20 years for heating systems.

Besides the four main scenarios, we also calculate seven sensitivity runs based on the ‘Diversified’ scenario. These include increased capital recovery factors (CRFs) for refurbishment activities, additional renovation barriers focusing on the share building surface with improved thermal properties, gas and liquid fuel potential restrictions and prices as well as the potential availability of solar thermal collectors. Table 6 shows the names of the sensitivity runs together with a description of which parameters have been varied.

Table 6 Description of calculated sensitivities based on the ‘Diversified’ scenario

In general, the defined scenario and sensitivity settings are the same in all countries. The only exception are the prices for gas and liquids, which differs from country to country (see Fig. 2).

Results

For the four scenarios and seven sensitivities calculated in this work, various parameters were analysed and are presented in this section. This includes total system costs, final energy demand, the share of thermal renovation on total refurbishment activity changes in energy needs per gross floor area and in u-values of different components, as well as the utilisation of roof area for solar thermal collectors and PV. These are presented and discussed separately in the following subsections.

Total system costs

The total system costs considered in this work are the sum of the capital costs for refurbishment activities, the capital costs for heating systems and the running costs for heating systems in all residential and service buildings of all countries of EU-27 over a defined period. The running costs are hereby made up of O&M and energy costs (see also ‘The optimisation model Invert/Opt’ section). The following Fig. 3 shows these costs calculated for the four scenarios for the entire EU-27 for three different periods, 2021–2030, 2021–2040 and 2021–2050.

Fig. 3

Total system costs for space heating and hot water generation in buildings, including refurbishment activities over different time periods for EU-27 for the calculated scenarios

Total system costs for space heating and hot water generation in residential and service buildings in EU-27 over the period from 2021 to 2050 are calculated to be in the range of €11,400 to €11,800 billion for the different scenarios. The ‘Low restrictions’ scenario hereby results in the lowest total costs, which is logical given the objective function of the calculations. At the same time, the ‘Low efficiency’ scenario, which enforces a high share of maintenance on the total refurbishment activities, leads to the highest total system costs. The difference between both scenarios is around 4%. Interestingly, even the ‘Increased renovation’ scenario, which enforces a remarkable increase in refurbishment activities, leads to lower total system costs compared to the ‘Low efficiency’ scenario. Looking at the results at the country level, it turns out that not in all countries the ‘Low restrictions’ scenario is the cheapest. In HR, HU, MT and RO, the ‘Increased renovation’ scenario leads to even lower total system costs compared to all other scenarios. This is due to comparably low costs for thermal renovation in combination with comparably high saving potentials in terms of running costs. In contrast, PT is the only country in which the ‘Low efficiency’ scenario leads to the lowest total system costs. This is due to a comparably lower share of running costs on total systems costs combined with very low saving potentials in terms of running costs.

Final energy demand

The four calculated scenarios obviously lead to differences in the resulting final energy demand for space heating and hot water generation (see Fig. 4). Even the ‘Low efficiency’ scenario results in a remarkable reduction in final energy demand of 29% between 2019 and 2050. The ‘Increased renovation’ scenario shows the highest reduction of 47%. This is due to a higher share of thermal renovation on total refurbishment activities (see also ‘Share of thermal renovation on refurbishment activities’ section) combined with an increased number of refurbishment activities over the simulation period. Also, in the ‘Low restriction’ scenario, remarkable savings of 44% are reached. In terms of energy carriers, the share of district heating and electricity decreases with decreasing final energy demand in the scenarios. The opposite is the case for solar heat and biomass. Solar heat hereby includes heat generation from solar thermal systems as well as from PV systems. This trend is generally similar in all large countries and can be explained in the following relationships: rooftop solar thermal systems on buildings are limited in size and potential heat generation per building. Therefore, with reduced heat demand in the buildings, the share that can be supplied by solar thermal systems increases. Biomass resources are foreseen to be scarcely available for space heating and hot water generation in the future and, therefore, severely restricted in the modelling. At the same time, heat supply from biomass is a comparably cheap option. Therefore, the absolute amounts of biomass used in the different scenarios in the different countries are similar, but with decreasing energy demand for space heating, the share of biomass in the overall heat supply increases.

Fig. 4

Final energy demand for space heating and hot water generation in buildings for EU-27 for the calculated scenarios

The final energy demand for space heating and hot water generation in EU-27 buildings in 2050 calculated for the seven sensitivities compared to the diverse scenario is shown in Fig. 5. It can be observed that with higher CRF of refurbishment activities, the final energy demand increases. This is logical because refurbishment activities become less cost-efficient compared to changes in the heat supply systems. A double CRF leads to reduced savings of nearly 6 percentage points (from 41 to 35%). An even stronger reduction of savings of around 7 percentage points is calculated in the sensitivity ‘add renov barriers’. The sensitivities related to the prices and availability of gaseous and liquid fuels show a low impact on the thermal renovation activities (see also ‘Share of thermal renovation on refurbishment activities’ section) and thus also on the resulting final energy demand. However, the split of energy carriers used for space heating and hot water generation changes. Without restrictions on liquid and gaseous fuels and same prices as in the other scenarios and sensitivities, more liquid fuels are used. With also lowered prices, gas becomes more competitive and partly replaces liquid fuels, district heating, electricity and heat pumps, and small amounts of biomass. The ‘no solar thermal’ sensitivity shows a higher reduction in final energy demand compared to the diverse scenario and a remarkable shift from solar thermal to electricity and heat pump use. Here, several effects can be observed: (a) the energy needs calculated in the model also depend on the energy consumption costs (see also ‘Calculation of energy needs for space heating and hot water generation’ section), thus, houses which need to buy the energy tend to have a lower calculated energy need than those which have a system with high investment but low running costs like solar thermal systems; (b) the energy losses of solar thermal hot water generation are larger than those of heat pumps due to the larger hot water storage tank; (c) more roof area is available for PV, thus, more PV electricity replaces other heat generation technologies with lower efficiencies.

Fig. 5

Final energy demand for space heating and hot water generation in buildings for EU-27 in 2050 in the sensitivities

Share of thermal renovation on refurbishment activities

Figure 6 shows the share of thermal renovation on the total number of refurbishment activities within the different calculated scenarios for each EU-27 country. In the ‘low_eff’ scenario, this share is exactly 35%, as is the exogenously defined maximum share for this scenario (see Table 5). In the ‘diverse’ scenario, this exogenously defined maximum share is 80%. As can be seen in the figure, nearly all EU-27 countries show this maximum share in the ‘diverse’ scenario: only AUT, MLT and SWE have shares slightly below 80%. This is because, in these countries, in some building segments, avoiding CO₂ emissions only via heating system change is more cost-efficient than any combination of heating system change and thermal renovation. In the ‘low_restric’ scenario, a higher share of thermal renovation is calculated in all countries compared to the ‘diverse’ scenario. This also applies to those countries that did not fully exploit the upper limit of thermal renovation in the ‘diverse’ scenario (AUT, MLT and SWE). The reason is that in those building segments that fully exploited the maximum share in the ‘diverse’ scenario, an even higher share of thermal renovation is economically feasible for avoiding CO₂ emissions. In 20 out of the EU-27 countries, this share is again equal to the exogenously defined maximum share of thermal renovation of 90%. This reflects a high economic potential of thermal renovation for avoiding CO₂ emissions compared to the change of the source and technology for heat supply. In the ‘inc_renov’ scenario, the length of the refurbishment cycles for building shell components is reduced by 1/1.4. This leads to increased refurbishment activities in the scenario time frame between 2019 and 2050. In other words, even currently (in 2019), relatively newly constructed buildings or recently refurbished buildings must be refurbished (again) until 2050. Nevertheless, very high shares of thermal renovation on total refurbishment activities are calculated for this scenario in many countries: 19 countries show a share of 90%, which is again the exogenously defined maximum, and 8 countries show a share above 80.

Fig. 6

Share of thermal renovation on refurbishment activities for the different countries in the period between 2019 and 2050 in the calculated scenarios

A comparison of the average share of thermal renovation on total refurbishment activities at EU-27 level for all scenarios and sensitivities is represented in Fig. 7. In addition, the figure shows the exogenously defined maximum shares (see also Table 5) and the annual thermal renovation rates. It can be observed that for most scenarios and sensitivities, the defined maximum shares of thermal renovation on total refurbishment activities are implemented. The sensitivities related to the capital recovery factor (crf + x%) and the additional renovation barriers form the exception here. In those, a slightly lower share of thermal renovation is calculated as cost-optimal by the model due to the applied changes in input parameters. The figure also clearly shows that the share of thermal renovation activities and the annual thermal renovation rates are directly proportional; the exception here is the ‘inc_renov’ scenario, in which a higher annual thermal renovation rate is triggered by the exogenously decreased length of refurbishment cycles.

Fig. 7

Share of thermal renovation on refurbishment activities and annual thermal renovation rate for entire EU-27 in the period between 2019 and 2050 in the calculated scenarios and sensitivities

Energy needs per gross floor area

The effects of the different scenario settings on the energy needs per gross floor area, including user behaviour,⁷ in the different building segments in Austria, are shown in Fig. 8. The figure shows the specific energy needs of each building segment on the y-axis and the size of the building segments in terms of heated gross floor area on the x-axis. The red area on the right side of the figure for each scenario reflects the building segments newly constructed during the scenario time frame. As expected, the scenario settings have no effect on these building segments, and the red area is the same for all scenarios. The black bars on the left side of each scenario diagram reflect the building segments that are not refurbished during the scenario time frame. As can be seen in the figure, these have the same size in all scenarios except the ‘inc_renov’ scenario. In the latter scenario, also the buildings that do not undergo refurbishment in the other three scenarios have to be refurbished and can be found whether in the grey or blue bars. The grey and blue bars reflect those buildings that are not demolished and are refurbished during the scenario time frame. Buildings in grey are those undergoing a maintenance activity, and buildings in blue are those undergoing a thermal renovation. The bright green part on top of the blue bars reflects the energy needs saved through the thermal renovation activities. It can be observed that the blue area in the ‘low_eff’ scenario is smaller than the grey area. This results from the defined constraints on the share of thermal renovation on total refurbishment activities (see Table 5). In all other scenarios, the share of blue bars is remarkably higher than the share of grey bars due to lowered restrictions on the share of thermal renovation. As discussed with regards to the previous figure, here, the difference between the share of blue bars and grey bars in the ‘diverse’ and the ‘low_restric’ scenario can be interpreted as the cost-efficient shift from maintenance to thermal renovation visible due to lowered restrictions.

Fig. 8

Specific energy needs for heating considering user behaviour (y-axis) over heated gross floor area of the building stock (x-axis) distinguishing no action, maintenance, thermal renovation and new construction for Austria for the calculated scenarios and two sensitivities

The same graphs as shown for Austria for different scenarios and sensitivities in Fig. 8 are shown for various countries for the ‘diverse’ scenario in Fig. 9. Differences between the countries can be observed: in SE, PL and FR, a remarkable increase in gross floor area between 2019 and 2050 is assumed in the scenarios (visible by the difference of total gross floor area and the end of the black continuous line), while in DE and especially IT and BG, much lower to nearly no increase is assumed. This leads to different shares of new buildings (in red) on the overall building stock. The difference between the black continuous line and the black dashed line shows the reduced demand from the buildings already existing in 2019. The shape of the lines is somewhat similar in the different countries; SE, however, shows a lower difference compared the other countries. This can be explained by lower technical heat-saving potentials due to already more efficient building stocks together with lower differences in heat saving and heat supply costs. In contrast, DE and FR show high economic saving potentials represented also in the size of the green bars.

Fig. 9

Specific energy needs for heating considering user behaviour (y-axis) over heated gross floor area of the building stock (x-axis) distinguishing no action, maintenance, thermal renovation and new construction for ‘diverse’ scenario for the countries SE, PL, DE, FR and BG

Figure 10 then shows the changes in energy needs per gross floor area split up between different construction periods of the buildings for the four calculated scenarios compared to the base year of the calculations. It can be observed that older buildings show higher energy needs per gross floor area in the base year as well as higher relative and absolute savings in the different scenarios. As expected, energy needs decrease most in the ‘Inc_renov’ scenario, second most in the ‘low_restric’ scenario, third most in the ‘diverse’ scenario and the least for the ‘low_eff’ scenario. These developments are similar in all construction periods.

Fig. 10

Changes in specific energy needs considering user behaviour for heating in buildings from different construction periods between the base year and 2050 for all EU-27 buildings in the calculated scenarios

U-values

Thermal renovation measures mainly aim at reducing the thermal transmittance of the building shell quantified via the u-values of their different components. Figure 11 shows the changes in the u-values in the different components, scenarios and construction periods in the form of a boxplot. The boxplot looks similar to the boxplot of the energy needs for heating in Fig. 10. Older construction periods start at higher u-values and show a larger decrease in absolute and relative terms compared to newer construction periods. The most significant decrease in absolute terms can be observed for windows upgrades. In contrast, basement insulation is performed less often (or the least).

Fig. 11

Changes in u-values in buildings from different construction periods between the base year and 2050 for all EU-27 buildings in the calculated scenarios

Utilisation of roof area for solar thermal collectors and PV

As described in ‘Calculation of delivered energy, costs and emissions for possible options’ section, the model Invert/Opt also considers solar thermal collectors and PV systems installed on the buildings’ roofs. The following Fig. 12 depicts utilisation of roof area for solar thermal collectors and PV systems in ES and DK for the ‘diverse’ and ‘low_restric’ scenarios and for the ‘no solar thermal’ sensitivity. On the x-axis, the figure shows the share of buildings that install a solar thermal and/or PV system in the country in the scenario; on the y-axis, the figure shows the share of the roof area of the individual buildings that install whether a solar thermal, a PV or both systems. The arrangement of the buildings from left to right follows the following logic: first buildings without a solar system are shown, second buildings with higher shares of solar thermal than PV and third buildings with higher shares of PV than solar thermal are shown. The figure shows that in all scenarios and sensitivities (shown in the figure) the share of roof area with PV systems installed is higher than the share roof area with solar thermal systems. In some cases, the share of roof area on individual buildings for solar thermal collectors is higher than PV, in ES around 15% of buildings, in DK less than 5%. We further see in the figure that the difference between the ‘diverse’ and the ‘low_restric’ scenarios in terms of utilisation of roof area for solar technologies is neglectable in both countries. In the ‘no solar thermal’ sensitivity, obviously no solar thermal systems are installed. At the same time, the full technical potential of PV systems is exploited in both countries. In the ‘diverse’ scenario in ES, around 83 TWh of electricity is generated by PV, of which 43% is used in appliances in the buildings, 38% exported to the grid and 19% used for heat generation in the buildings. In DK, 8 TWh of electricity is generated by rooftop PV, 39% used in appliances in the buildings, 25% exported to the grid and 36% used for heat generation in the buildings.

Fig. 12

Utilisation of roof area for solar thermal collectors (green) and PV (red) for Spain and Denmark in the ‘diverse’ scenario, the ‘low_restric’ scenario and the ‘no_solar_thermal’ sensitivity run

Discussion, conclusions and outlook

For a drastic reduction of carbon emissions from heat supply in buildings, many currently installed supply systems must be changed, and the energy needs must be reduced. However, it is not straightforward to identify which technologies should be used and how much energy needs should be reduced in different building archetypes and building segments to avoid carbon emissions until 2050 at the lowest possible costs. The existing building stocks in Europe are heterogenous, and demand characteristics are still not fully understood. There exists a variety of options for a drastic reduction of carbon emissions from heat supply in buildings, both for low carbon heat supply and for reducing energy needs. Also, carbon–neutral resource potentials are restricted, and available amounts and related prices have complex interrelationships with each other and are subject to uncertainties.

This study contributes to a better understanding of meaningful combinations of heating system change and thermal renovation by calculating the effects of different restrictions for refurbishment activities as well as several sensitivities on refurbishment barriers and resource potentials with a bottom-up building stock model minimising overall system costs. Special features of this study are the representation of residential and service buildings of all EU-27 countries with a remarkable number of different building archetypes and segments in each country, the consideration of a broad set of passive (refurbishment) and active (heating system change) measures to reduce carbon emissions, and the identification of that combination of active and passive measures in each building segment that leads to lowest system costs while taking into account countrywide resource restrictions.

The calculated scenarios reveal the following result: strongly restricting the share of buildings that are allowed to implement a thermal renovation when the lifetime of the building shell is reached leads to higher system costs compared to relaxed restrictions. Allowing 90% of the buildings in the stock of each EU-27 country to implement a thermal renovation (‘Low restrictions’ scenario) leads to around 4% lower system costs until 2050 compared to restricting the share of thermal renovation to a maximum of 35% (‘Low Efficiency’ scenario). These 4% equal around 400 billion EUR in the 30-year period between 2021 and 2050 or around 13 billion EUR per year. Especially in older buildings, a combination of heating system change and thermal renovation is cheaper compared to only replacing the heating system to avoid CO₂ emissions. However, also in newer buildings, the implementation of a thermal renovation is often cost-efficient. If the model allows it (in the ‘Low restrictions’ scenario), a remarkable share of buildings constructed after 2000 implement a thermal renovation. This share even increases when shortening the refurbishment cycles (in the ‘Increased renovation’ scenario) and thus forcing a larger share of newer buildings to implement any form of thermal renovation activity on the building shell. In many cases, at least the windows are exchanged for windows with lower u-values.

Furthermore, the calculations show that the final energy demand for certain energy carriers decreases with decreasing restrictions on thermal renovation, while for others, this is not the case. Especially the final energy demand for district heating decreases in absolute as well as in relative terms in the scenarios with lower restrictions on thermal renovation. This shows that a thermal renovation, in many cases, is cost-efficient if the building is connected to a district heating system. Solid biogenic energy carriers instead are used as much as they are available in many countries, no matter which restrictions are set for thermal renovation. The reason is that they provide cheap decarbonisation options via different technologies and that they can be used in more buildings than is possible to supply due to the assumed resource restrictions. Also, solar thermal collectors and PV systems are installed to a remarkable extent in all scenarios. Like biogenic energy carriers, the share of solar energy on the final energy demand increases with decreasing final energy demand. The reason is the constant size of the systems on the rooftop leading to larger shares of heat demand covered by solar thermal with reduced heat demands.

Overall, the calculations indicate that under the assumed price developments and resource potentials for energy carriers, the assumed costs for supply technologies and for refurbishment as well as thermal renovation measures, a high share of thermal renovation measures is cost-efficient to reach a 95% reduction in direct CO₂ emissions for space heating and hot water preparation in the EU-27 building stocks. At the same time, the calculations are, of course, subject to various uncertainties. The greatest uncertainties in the calculations are assumed to be in energy carriers’ prices and the calculated costs and effects of thermal renovations. Besides the assumption of unchanged district heating prices between current levels and 2050, as mentioned before, the prices for the grid-based energy carriers gas and electricity might also deviate remarkably from the assumed prices. For both energy carriers, it is rather uncertain in which order of magnitude the grid fees will develop, and the assumed grid fees are expected to be on the lower end of potential developments. Both the simplification of district heating price evolution as well as the low estimated grid fee developments are expected to lead to an increased cost-efficiency of thermal renovation in the current calculations, i.e. thermal renovation might be even more beneficial than in the presented calculations when considering these uncertainties. At the same time, the wholesale prices for liquid and gaseous fuels could be lower and the available resource potentials could be higher than assumed in the scenarios and lead to lower cost-efficiency of thermal renovation measures. However, the calculated sensitivities show that unlimited availability of liquid and gaseous fuels and remarkably lowered prices does not affect the cost-efficient share of thermal renovation.

The uncertainties related to the calculated costs and effects of thermal renovation are expected to decrease the cost-efficiency of thermal renovation in the model runs. Even though the level of detail in the thermal renovation options considered in this study is comparably high, the considered renovation options are still a simplification of reality. In a sensitivity run, additional renovation barriers were taken into account, resulting from monument protection in older buildings, extraordinary exterior surfaces like stucco or bricks, and from the fact that thermal renovations are often not implemented as planned. All this leads to lower shares of surface area that is treated or treated with the same measure, and potentially that thermal bridges are overlooked. This leads to lower saving effects and higher costs. The related sensitivity run showed a decrease of cost-efficient savings around 7 percentage points. Furthermore, in the scenarios we calculated with 2% interest rate and 30 years of lifetime for refurbishment activities. Sensitivity runs increasing the capital recovery factor up to 100% also showed remarkable effects on the cost-efficient saving levels up to minus 5 percentage points. At the same time, it also must be noted that a thermal renovation of an existing building not only decreased energy demand and resulting energy expenditures. It also increases the comfort for the users and the value for the owners. Both the rent as well as the selling price of renovated buildings tend to be higher than those for not renovated buildings. Such revenues for thermal renovation activities are not taken into account in the analysis and would increase the economic viability of thermal renovation compared to heating system change.

In addition, also the estimation of the current energy needs for space heating and hot water generation in buildings according to EN ISO 13790 (CEN, 2008) are remarkably uncertain, even though user behaviour and rebound effects are integrated into the Invert/Opt model. Recent comparisons of calculated demand, literature values and measured consumption for local building stocks indicate that the current energy needs in older buildings might be overestimated and in newer buildings might be underestimated. Thus, potentially the economic heat-saving potential in older buildings is overestimated, while for newer buildings, it might be underestimated. The overall effects on the countrywide calculations are difficult to predict. Thus, it is of high importance to further investigate the difference between calculated and measured energy demand in the buildings to improve the understanding of potential costs and effects of thermal renovation interventions. This should also consider socio-cultural characteristics of users and their behaviour to better understand potential future changes due to demographic change like changes in the age structure or the level of education.

Overall, the calculations show that assuming low technical restrictions and low capital recovery expectations for refurbishment activities together with shortened length of refurbishment cycles would lead to cost-efficient savings of up to 47% of final energy demand between 2019 and 2050. Assuming less favourable conditions for thermal renovation, the cost-optimal level of heat savings in buildings for overall EU-27 could be suspected at around 1/3 of final energy demand. With several unfavourable conditions occurring together, cost-optimal saving levels could even be suspected at around 1/4 of current final energy demand. However, strong and coherent policy measures are needed to drive the implementation of the transformation. Among other measures, fossil energy carriers must be banned or imposed with a strong carbon price to avoid their utilisation and availability on the market or in the grids. Financing and subsidising investments in thermal renovation are key to overcome the high upfront investments and allow for higher expectations on the CRF. Also, many more craftsmen able to implement thermal renovation activities are needed and must be trained.