Introduction

The crystallization behavior of mold slags plays an important role in the continuous casting of liquid steel. The mold powder is added to the top of the liquid steel in the mold and is liquefied. The slag is subsequently trapped in the gap between the strand and the water-cooled copper mold and solidifies. A glassy layer appears and is in contact with the mold, and a liquid slag layer is in contact with the strand. In between these layers, a crystallized layer with various crystals is formed. The sizes, shapes, and quantities of these crystals vary depending on the mold slag itself and other conditions such as the temperature gradient of the slag film or the position within the layer. To investigate the crystallization behavior of mold slags at near-service conditions, the double hot thermocouple technique (DHTT) was developed. In this technique, the liquid slag is stretched between two platinum wires that are heated to different temperatures.[1,2] The equipment consists of the experimental unit, the hot thermocouple drivers, and a video capture system. The experimental unit is a housing chamber for the wires, or it can act as a vacuum chamber.[3,4] Other devices, include a supplemental heater, located in the chamber at the bottom[1,2] or surrounding the sample to reduce heat loss from the sample surface into the ambient environment (Figure 1(a)). Two heating wires made from type-B thermocouples welded without a bead are situated close to the heater. The hot thermocouple driver enables simultaneous measurement of the temperature, while the thermocouple is heated. For this purpose, the electric current is rectified into a half-wave using a silicon-controlled rectifier. One half-period is used in the heating cycle, and only 1/3 of the following period is used in the temperature measurement to reduce the sampling noise.[1,2] In certain cases, the equipment includes an air-cooling device to support the high cooling rates of the sample for isothermal experiments (see below).[4,5]

Fig. 1
figure 1

Schematic illustration of the DHTT set up according to (a) the literature[9] and to (b) the newly developed equipment with (c) the related stretching devices: (1) U-shaped B-type thermocouple, (2) slag film, (3) additional heater, (4) ceramic rod of the stretching device, (5) furnace chamber, (6) opening for observation, (7) H-shaped platinum wire with additional B-type thermocouple, (8) leg of the H-shaped platinum wire, (9) U-shaped platinum wire with additional B-type thermocouple, (10) refractory lining, and (11) Type S thermocouple

Full size image

The crystallization behavior can be investigated via 3 different experimental procedures.[6] For isothermal experiments, the sample is liquefied between the thermocouples and quenched to the desired temperatures to investigate crystallization. Subsequently, the images are evaluated to create time–temperature–transformation (TTT) diagrams for defined crystallinities. For the continuous cooling experiments, the sample is cooled between both thermocouples with defined cooling rates after liquefaction, and additional continuous cooling transformation (CCT) diagrams can be created to show the beginning and end of the crystallization. For continuous cooling experiments with different thermal gradients, the sample is heated to a maximum temperature (e.g., 1500 °C) between both thermocouples. One side is quenched to 600 °C, and the other is cooled at a predefined cooling rate. The resulting pictures are evaluated by partitioning the slag into areas defined by the morphology of the crystals.

Many authors have used the DHTT equipment to characterize the melting[6,7,8,9] and crystallization behaviors of different slags via TTT and/or CCT diagrams.[6,7,9,10,11,12,13,14] Furthermore, this device is used to observe the crystallization that occurs when the slag is exposed to selected temperature gradients[3,15,16] and to investigate the effect of water vapor.[14,17] This method has also been applied to measure the heat transfer of a completely glassy and crystalline slag[18] through slag films and the effective thermal diffusivity of molten slags.[19,20] Furthermore, an external potential has been applied to a liquid oxide to study the effect of different electrical potentials[21] on the formation of bubbles and their subsequent dissolution in liquid silicates.

Currently, the DHTT equipment and data evaluation suffer from certain deficiencies. Thermal calculations of the temperature profile of a mold slag during an experiment with a temperature gradient showed that the minimum temperature is expected to occur within the sample due to heat loss to the environment from the sample’s surface. Nevertheless, the minimum is intended to be at the colder wire.[22] Another disadvantage is the design of the thermocouples. The common U-shaped thermocouples do not ensure sufficient stretching of the liquid slag and lead to the formation of a droplet between the platinum wires in most cases. This situation impedes the observation of the crystallization behavior of slags with a certain content of coloring oxides. Furthermore, only pictures or videos have been used thus far to represent the results of these investigations, which do not allow for a simple comparison of the crystallization behavior of different slags.

Based on the state-of-the-art technology described above, the following objectives were chosen for this research work. The heat loss of the slag film should be decreased to ensure a continuous temperature decrease from the hot to the cold wire without an intermediate minimum. Further measures should be taken to enable the creation of a slag film with a uniform thickness and a defined rectangular shape. Finally, measurements with the modified equipment should be represented and evaluated in a manner that supports reasonable characterization and comparison of different slags. Therefore, the set up of the equipment, the data evaluation, and the result display have been modified to allow for conclusions based on the applicability of the technique for newly developed slags under near-service conditions.

Experimental

Setup of the Developed DHTT Device

Based on the device mentioned previously,[1,2] the DHTT equipment was modified. The new apparatus included a furnace chamber with heating units, a stand with a camera and objective, a controller, and an image-recording device (Figure 2). The numbers given in round brackets within this subchapter refer to the respective components given in Figures 1(b) and (c). The furnace (5) consisted of a steel shell lined with an alumina silicate insulating refractory (10). The furnace chamber had a cylindrical shape with a 30 mm diameter and 50 mm height. Two lateral holes located opposite each other allowed the two components ((4) with (7) or (9), respectively) used in the heating and stretching of the specimen to enter, and these components are further explained below. An additional opening for loading the furnace with the specimen was situated at the top and could be closed by a special cover plate (6) made of the same refractory material as the furnace to reduce heat loss. Observation was possible through a hole in the lid, which was covered by a quartz window to protect the objective. A small resistance heater (3) made of a corundum tube with wire winding was placed at the bottom to heat the entire chamber to the lower desired temperature.

Fig. 2
figure 2

Setup of the DHTT-equipment: (1) furnace with heating device, (2) height-adjustable stand with camera and objective, (3) temperature control PC monitor, (4) control unit for the furnace, (5) control unit for the heating device, and (6) PC for data storage and visualization

Full size image

The heating unit (left-hand-side illustration in Figure 1(c)) inserted into the opening on one side of the furnace was composed of an H-shaped platinum/rhodium wire (Pt/Rh 70/30) with a diameter of 0.5 mm. The H-shaped heating wire (7) was fixed to two copper rods housed in a ceramic body (4). The outer ends of these copper rods were connected to the power supply via banana plugs. In contrast to the equipment mentioned previously,[1,2] the thermocouple was not applied for heating. Instead, a Type-S thermocouple was welded (11) to the heating wire at a position in direct contact with the molten slag during the experiment. The tails of the thermocouple were fed out of the furnace via two further holes in the ceramic body and connected to the associated interface. A so-called stretching device ((4) with (9)) served to mount the slag film between itself and the H-shaped platinum wire. This device represented the cold boundary, and the hot boundary was the horizontal bar of the H ((4) with (7)). The stretching device was made of a 0.5 mm loop-shaped platinum/rhodium wire (Pt/Rh 70/30) (9) mounted to a corundum rod (4). This wire was inserted laterally opposite the inlet of the H-shaped wire (7) and was clamped to a bracket outside the furnace chamber that could be moved via a screw drive. A Type-S thermocouple ((11) of (9)) made from Pt-Pt10Rh wires with a diameter of 0.25 mm was welded to this device. It allowed for measurement of the furnace temperature close to the sample. Thus, the furnace chamber can be heated to the selected cold-wire temperature at the slag film level, and no additional heating of the stretching device is necessary. A detailed description of the temperature control and the data acquisition is given elsewhere.[23]

Experimental Procedure

For the first set of experiments, a model slag with the composition 3K2O·11GeO2 was used because of its congruent melting/crystallization behavior, transparency, and the clearly visible opaque crystals it forms. This choice facilitates observation of the crystallization behavior. A slag related to the alternative fluorine-free mold slags was also analyzed. The chemical compositions of the investigated slag samples are given in Table I.

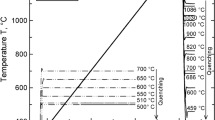
Table I Chemical Compositions of the Investigated Slags
Full size table

The raw materials were homogenized with an oscillating disk mill, melted in a muffle furnace within a platinum crucible, quenched to room temperature, and ground to a fine powder. From this fine material, pills with a height of approximately 1 mm were pressed. The DHTT furnace was heated to the selected temperature of the cold end. For these investigations, temperatures of 600 °C, 700 °C, 800 °C, and 900 °C were selected. The hot wire was heated to 1300 °C to represent the hot face of the slag layer in the mold. This temperature was selected in order to reduce possible evaporation of volatile components. Furthermore, at temperatures above 1300 °C no crystallization will be observed for mold slag compositions. For the 3K2O·11GeO2 sample, the temperature was reduced to 1150 °C because of its lower melting point compared to the mold fluxes. After the desired temperature was reached, pieces with edge lengths from 2 to 3 mm were cut from the tablet, positioned on the crossbar of the H-shaped wire, and liquefied. To control the total liquefaction of the sample, the slag spanned the direction of the inlet of the H-shaped platinum wire for a short time. At the same time, the bubbles formed during melting were eliminated. During the experiment, especially for MS 1, bubble formation could be observed again. Removal of these bubbles would have required opening the cover plate influencing the temperature profile of the sample. If a homogeneous liquid was present, the slag (2) was immediately stretched in the opposite direction. The distance between the hot and the cold wires was 3 mm for all measurements. Together with the stretching device, the legs of the H-shaped wire aided in defining the shape of the slag film. By choosing a suitable sample mass, a slag film that was sufficiently thin for observation was achieved. This result was better than the results from the standard device with two heated U-shaped wires and without a defined slag layer boundary between the wires. Due to the action of the slag’s surface tension, the width of the slag film decreased and the middle of its length thinned. The slag was exposed to the selected temperature gradient for a selected dwell time. The dwell time was defined by the steady state achieved after a sufficient crystallization time. In this research, it was achieved after about 10 minutes for both slag compositions, because crystallization was completed after this point. For further observations, the specimens were quenched to room temperature.

To estimate the maximum temperature based on the position within the slag film, slag films of MS 4 (Table I) were mineralogically investigated after the experiments using a scanning electron microscope that included energy dispersive X-ray spectroscopy. These results were subsequently compared with the thermodynamic calculations under equilibrium conditions.

Data Evaluation

Image editing process

For the data evaluation, the crystalline fraction of the sample must be determined for the selected pictures taken during the experiment. This evaluation is based on the area fraction of the crystallized domain relative to the total slag film area. After marking the respective areas on the digital images via recoloring of the crystallized areas of the original pictures (Figure 3(a)), a special image-editing program was used to calculate the crystalline area. The interface nucleation on the slag/cold wire interface was primarily observed. Therefore, the crystallization proceeds along the viable perimeter of the already crystallized domain. The length of this viable perimeter was also determined and used in the crystal growth-rate calculations. At least three experiments were performed for each temperature gradient. The mean value of the crystalline fraction dependence on time was calculated for each temperature gradient and is represented in a diagram. Nevertheless, this type of display alone is not satisfactory to compare the crystallization behavior of different mold slags. Thus, in this study, further quantitative graphical representations were developed based on the discretization of the slag film images. To evaluate the necessary resolution of the discretization, each colored picture of the experiments with the model slag was sliced into layers of 0.5, 0.25, and 0.1 mm (Figure 3), e.g. Figures 3(c) and (d) representing a slice of Figure 3(b) close to the cold or the hot side, respectively. The obtained results showed that fragmenting the slag film images into slices of 0.1 mm was reasonable. Therefore, this procedure was used in the image editing process for all further investigations.

Fig. 3
figure 3

Image editing process for crystallinity calculation: (a) picture of the slag film at the selected time, (b) recoloring of the crystallized area of the original picture given in (a) and definition of areas every 0.25 mm, (c) slice close to the cold, and (d) slice close to the hot wire used in the calculation of the crystalline fraction within each slice: (1) crossbar of the H, (2) leg of the H, (3) welding point of the type S thermocouple, and (4) U-shaped stretching device

Full size image

Representation of the results

Slices of the slag film images that were 0.1 mm thick were produced. For any arbitrary slice and time, the absolute crystallinity, c, was defined by the ratio of the crystallized area at the respective time to the total area of the slice. Furthermore, the relative crystallinity, cr, was defined by the ratio of the crystallized area in that slice at time, t, to the maximum crystallized area in the same slice during the experiment, i.e., the steady state achieved after a sufficient crystallization time. The steady state depends on the crystallization behavior of the associated slag. Therefore, the time as well as the maximum crystalline fraction varies for different slag compositions. The results were represented differently (Figure 4). First, the mean value of the maximum absolute crystallinity, c, observed during the experiment (i.e., the value representing the steady state) was determined for each slice and temperature gradient. These data were plotted in a diagram with a dependence on the distance from the cold wire for each temperature gradient (Figure 4(a)). Second, the time until a defined relative crystallinity, cr, was achieved was represented by the dependence on the distance from the cold wire (Figures 4(b) and (c)). Therefore, the relative crystallinity was calculated for all the slices with a dependence on time, and the crystallization time necessary for the defined relative crystallinity was determined from this relationship for any slice. With this information, charts of the time vs distance from the cold wire were calculated, and corresponded to defined relative values of the crystallinities. For this paper, values of 0.5 and 95 pct were selected to represent the start and end of the crystallization. Additionally, because the volume nucleation only plays a minor role, the crystal growth rates that depend on the experimental time were calculated for each temperature gradient via Eq. [1]:

Fig. 4
figure 4figure 4

Graphical representation of (a) the maximum absolute crystallinity for MS 1 and MS 2 and (b) the time for the start (cr = 0.005) and (c) end (cr = 0.95) of the crystallization depending on the distance from the cold wire for all the investigated temperature gradients

Full size image
$$ \nu = \frac{1}{u}\frac{{{\text{d}}A}}{{{\text{d}}t}}. $$
(1)

In this work, ν is the crystal growth rate [ms−1], U is the viable perimeter [m], A is the crystalline area [m2], and t is the elapsed time [s]. The values of the same temperature gradients were depicted in a diagram. Because of their fluctuations, a trend was not easily identified, and a polynomial regression was used (Figure 5).

Fig. 5
figure 5

Crystallization growth rate for MS 1 and MS 2 for all the temperature gradients: (a) overview and (b) magnification of the first seconds

Full size image

Results and Discussion

DHTT Investigations

According to the two-component system of K2O-GeO, MS 1 showed congruent crystallization behavior. The slag and crystal display the same composition (Table I), and, therefore, the liquid diffusion did not contribute as a rate-limiting step. Independent of the temperature gradient, the first crystallization occurred in contact with the cold wire. Subsequently, a crystal front grew in the direction of the increasing temperature. Because of the formation of this crystal front, a shift was observed in the position where the last crystals were detected after the experiment in the direction of the hot wire with the decreasing cold-wire temperature. MS 2 showed similar crystallization behavior progressing from the cold wire for a temperature gradient of 1300/900 °C. However, if this slag was exposed to decreasing cold-wire temperatures, crystals also formed in contact with the platinum legs of the hot wire (i.e., the horizontal bars of the H). These crystal fronts grew in the direction of the slag film center and in the hot and cold side until they united with the crystals growing in the direction of the increasing temperature. With progressive crystallization, the crystal fronts from the legs adopted a bell-shaped appearance. These crystalline areas will obviously grow into the center of the slag film: Into the direction to the hot side, crystal growth rate will be reduced due to the increase of the temperature along with a decreased driving force. Into the direction of the cold side, viscosity will increase due to the temperature decrease. Both effects will reduce the crystal growth rate. Therefore, these crystal fronts show a bell shaped appearance with crystal growth toward the center of the slag film. However, with the increasing cold-wire temperature, the crystal fronts’ maxima were shifted in the direction of the cold wire. This position corresponds to the temperature of the maximum crystal growth rate. Because of the position of the maxima of the crystal fronts, they united earlier with the fronts from the stretching device if the temperature on the cold side was increased. This observation implies that the temperature of the cold wire lies below the maximum crystallization rate.

In Figure 4, possible display methods are shown for the investigated samples. Only the sum of information represented in these diagrams is advisable for the comparison of different slags. This observation is particularly true for the diagram representing the maximum crystallinity with a dependence on the position within the slag film. In this display, no information on the time needed to achieve complete crystallization is displayed, which is relevant for the characterization of the crystallization behavior of the slag.

The maximum absolute crystallinity is given in Figure 4(a). Due to the congruent solidification behavior of MS 1, a sharp decrease in the crystallinity at the position of the melting point was observed, as expected. However, this slag achieves high crystallinity values only within the crystalline area close to the cold wire. This observation might be explained by a certain thermal conductivity of the platinum wire or by the evaporation of small amounts of K2O during the experiment, which caused the remainder of the small amount of the liquid phase to contact the legs of the H-shaped thermocouple. If the cold-wire temperature decreased, the position corresponding to the melting point of the slag shifted toward the hot wire. This observation was also valid for MS 2, except for 1300/600 °C. In this case, the crystallization was not completed at the end of the experiment, and an increase in the crystallized area was still detected. Although MS 2 showed incongruent melting behavior, 100 pct crystallinity was achieved in close proximity to the cold wire and at a certain distance from it. A completely crystallized region might still contain liquid in the pores below the optical resolution of the device.

Figures 4(b) and (c) illustrate the time until the start (cr = 0.005) and end (cr = 0.95) of the crystallization with a dependence on the position within the slag film. For MS 1, the following relationships are important. With the decreasing cold-wire temperature, the undercooling representing the driving force for crystallization increases over a wider range, and the time for the start and end of the crystallization decreases. For 1150/600 °C and 1150/700 °C, immediate crystallization occurs for approximately half of the slag film. With the increasing cold-wire temperature, the driving force for crystallization is reduced, and the shape of the curve progression (revealing the 95 pct relative crystallinity) changed from a nearly exponential increase over time with an increasing distance from the cold wire to an S-shaped curve progression for 1150/800 °C and a nearly linear curve for 1150/900 °C. However, MS 2 has a slightly different behavior. For all four cases, this sample showed similar trends for the start of crystallization. The fluctuations at certain positions within the slag film, especially for the curve representing the end of the crystallization, can be explained by the formation of nearly bell-shaped crystallization fronts growing from the legs into the slag film. Despite these fluctuations, the time until the end of the crystallization tends to increase with the increasing cold-wire temperature, with the exception of 1300/700 °C. However, this latter result appears to be due to the formation of the bell shaped crystallization fronts from the legs of the platinum wire at the beginning of crystallization; a detailed description of the crystallization process has already been mentioned before. Due to this additional crystal front, the crystallization is completed faster within this area and the end of crystallization (cr = 0.95) is achieved within shorter times. This can be seen from the constant time values for the end of crystallization within certain distances from the cold side. Due to a lower viscosity and therefore an increase of the crystallization rate within this area for the temperature gradient of 1300/700 °C compared to the one of 1300/600 °C, the associated time values are lower. The higher crystallization rate for the temperature gradient 1300/700 °C at the beginning of the experiment can also be seen from Figure 5. Additionally, the calculation of the crystal growth rate with a dependence on the elapsed time offers Figure 5. It has to be considered, that this diagram represents the total crystallization progression independent on the position within the stretched slag. Therefore, effects taking place at the beginning of the experiment may be seen from the curve progressions, but effects taking place with increasing experimental time will not be observed due to superimposition. They can only be detected from Figures 4(b) and (c). Nevertheless, it provides necessary information for the characterization of the crystallization process and suggests another possibility for the comparison of slags. For temperatures of the cold side of 600 °C, 700 °C, and 800 °C, spontaneous crystallization occurs for MS 1 immediately after stretching, and the main crystallization process is completed within a few seconds. Therefore, it shows the highest crystal growth rate at the start of crystallization, but, subsequently, the crystal growth rate decreased rapidly to nearly zero and was significantly lower than that of MS 2. This can be explained by the congruent crystallization behavior of MS 1. In this case, chemical diffusion does not contribute as a rate-limiting step. By contrast, the highest crystal growth rate by far was observed for MS 2 at 1300/900 °C. Its higher driving force compared to MS 1 due to the higher temperature difference between the melting point and the investigated cold-wire temperature of 900 °C (melting points of MS 1 1062 °C and MS 2 1258 °C, respectively), and the lower viscosity of the remaining liquid phase facilitating diffusion lead to this behavior.

Mineralogical Investigations

The equilibrium slag composition of MS2 was determined via thermochemical calculations performed using the commercial software FactSage (Figure 6(a)). During cooling, wollastonite was the first crystal formed at 1258 °C. Subsequently, wollastonite and augite coexisted from 1245 °C to 1225 °C, where anorthite crystallized. At 1224 °C, no liquid was present. The mineralogical investigations of the DHTT-samples of MS 2 showed that for all the temperatures investigated, wollastonite was the phase that had the first contact with the liquid slag at the highest temperature. A front of alumina containing diopside and augite was close to this area. At the cold wire, additional anorthite was detected. These results are in good agreement with the thermochemical calculations. Combining the measurements with the calculations gives a representation of the paragenesis in the crystallized slags at a steady state with a dependence on the temperature and the distance from the cold wire (Figure 6(b)). This temperature distribution also applies to other slag samples.

Fig. 6
figure 6

Representation of (a) the phase composition of MS 2 with a dependence on the temperature in equilibrium and (b) paragenesis in the crystallized slags at a steady state with a dependence on the temperature and the distance from the hot wire

Full size image

Conclusion

This paper presents an investigation of the crystallization behaviors of transparent or translucent slags under defined temperature gradients using a modified DHTT method. The new setup overcomes the disadvantages of a minimum temperature located within the sample due to heat loss to the environment from the sample surface, and a minimum at the colder wire is intended.[22] This is realized by heating the furnace chamber to the cold-wire temperature. Therefore, the furnace temperature is controlled via the Type-S thermocouple of the stretching device positioned in the level of the slag film. In addition, this process also enables the observation of liquids that are translucent because of the formation of a sufficiently thin slag film layer within the newly developed H-shaped heating wire instead of a contracted liquid droplet between two U-shaped heating wires. Using the suggested graphical representations of the results, an evaluation of different slags with respect to their crystallization behavior was possible. The maximum crystallinity of different slags can be compared depending on the position within the slag film. However, this diagram alone does not reliably describe the crystallization process because no information is given on the kinetics. Therefore, additional information is offered by the representation of the crystallization time for selected crystallinities with a dependence on the position within the sample. Furthermore, the crystallization progress is described by the crystal growth rate with a dependence on time. As expected, it was demonstrated that the crystallization of a liquid with a congruent melting behavior shows both higher crystallinities and higher crystal growth rates primarily at the beginning of the experiment compared with the slags in which the liquid diffusion is rate determining because of incongruent crystallization. Certain positions within the liquid slag layer were allocated to the respective temperatures by comparing the results of mineralogical investigations with the thermodynamic calculations. Thus, an approximate temperature distribution within the slag film was determined, which is also valid for other slags if the distance between the platinum wires is constant. In this work, a distance of 3 mm was chosen.