Skip to main content

Advertisement

SpringerLink
Log in

A CFD-FEM Model of Residual Stress for Electron Beam Welding Including the Weld Imperfection Effect

  • Published:
Metallurgical and Materials Transactions A Aims and scope Submit manuscript

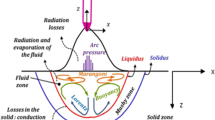
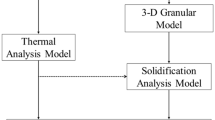
Abstract

Residual stress of electron beam welding (EBW) is associated with the heat transfer, fluid flow, and keyhole dynamics occurred in the process. In engineering, it was commonly simulated by pure heat conduction-based thermomechanical modeling with an experimentally calibrated heat source model. This method, however, is difficult to be used to consider the effect of weld imperfections such as the spiking and porosity defect. In this study, we proposed a novel combined computational fluid dynamics and finite element method (CFD-FEM) model to predicate the residual stresses of EBW. This model allows us to include the integral effect of heat transfer, fluid flow, and keyhole dynamics as well as process defects on residual stresses for the first time. A phenomenological heat source model dependent on the dynamic keyhole was considered in the CFD model part. A mapping algorithm was developed to build a new heat source model of FEM modeling part from the CFD simulations. Parametrical simulations and experiments of EBW of a 10-mm-thickness Ti-6-Al-4-V alloy plate were carried out and good agreements were obtained by the comparisons. It was shown that for deep penetration EBW the keyhole oscillates in radial and depth directions and the spiking defect occurs, particularly under large heat input parameters. Interestingly, the equivalent and principle residual stresses exhibits strong oscillations in the bottom part of welds along the welding direction, in which the amplitudes are around 9 pct (73.69 MPa) of the equivalent stress and 24 pct (121.84 MPa) of the principle stress in penetration direction, respectively, when the power of electron beam is 1.5 kW. As the power of electron beam increases, the effect of spiking on the residual stress enhances. When the welding power increases to 2.25 kW, the amplitudes of equivalent residual stress increase to 12 pct (119.2 MPa). Our results provide a quantitative method connecting the weld pool dynamics and process defects with the residual stress of EBW, which previously could be understood only in a qualitative way, and demonstrate the possibility of residual stress predications only from the information of materials and process parameters before welding, without the knowledge of post-weld profiles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Abbreviations

\( U \) :

Velocity

\( \vec{U} \) :

Movement speed of the free surface interface

\( T \) :

Temperature

\( T_{\text{ref}} \) :

Reference temperature

\( T_{\infty } \) :

Ambient temperature

\( T_{i} \) :

Temperature of the CFD element

\( p \) :

Pressure

\( p_{\text{f}} \) :

Free surface

\( p_{\text{r}} \) :

Recoil pressure

\( g \) :

Gravitational vector

\( c \) :

Specific heat

\( C\rho \) :

Heat capacity

\( K \) :

Heat conductivity

\( k_{i} \) (i = x, y, z):

Thermal conductivity in the x, y, and z direction

\( Q \) :

Volumetric energy generation

\( Q_{\text{total}} \) :

Total energy input

\( Q_{\text{d}} \) :

Dynamical keyhole-based heat source term

\( Q_{i} \) :

Heat flux of each element of FEM model

\( \vec{n} \) :

Unit normal vector

\( \overrightarrow {{t_{1} }} \), \( \overrightarrow {{t_{2} }} \) :

Unit vector orthogonal cutting, \( \overrightarrow {{t_{1} }} \) is perpendicular to \( \overrightarrow {{t_{2} }} \)

\( V_{i} \) :

Volume of the element of FEM model

\( h_{\text{r}} \) :

Radiant heat transfer coefficient

\( D^{P} \) :

Plastic matrix

\( D^{e} \) :

Elastic matrix

E :

Young’s modulus

\( \mu \) :

Kinetic viscous coefficient

\( \rho \) :

Density

\( \beta \) :

Thermal expansion coefficient

\( \phi \) :

Distant to the surface

\( \sigma \) :

Surface tension coefficient

\( \kappa \) :

Curvature

\( \varepsilon_{\text{r}} \) :

Surface emissivity

\( \sigma_{\text{s}} \) :

Stefan–Boltzmann constant

\( \Omega \) :

Heat source zone

\( d\sigma \) :

Stress increment

\( d\varepsilon \) :

Strain increment

\( \alpha \) :

Coefficient of liner expansion

References

  1. J.W. Elmer, and W.H. Giedt, T.W. Eagar: Weld. J., 1990, vol. 69(5), pp. 167-176.

    Google Scholar 

  2. H. Hemmer, and Ø. Grong: Weld. Join., 1999, vol. 4(4), pp. 219-255.

    Article  Google Scholar 

  3. D. Couedel, P. Rogeon, P. Lemasson, and M. Carin, J.C. Parpillon : Int. J. Heat Mass Transf., 2003, vol. 46(23), pp. 4553-4559.

    Article  Google Scholar 

  4. S. Rouquette, J. Guo, and P. Le Masson: Int. J. Therm. Sci., 2007, vol. 46(2), pp. 128-138.

    Article  Google Scholar 

  5. P. Lacki, and K. Adamus: Comput. Struct., 2011, vol. 89, pp. 977-985.

    Article  Google Scholar 

  6. H.J. Stone, S.M. Roberts, and Reed R.C (2000) Metall. Mater. Trans. A, vol. 31A, pp. 2261–73.

  7. C. Liu, B. Wu, and J.X. Zhang: Metall. Mater. Trans. B, 2010, vol. 41, pp. 1129-1138.

    Article  Google Scholar 

  8. J.H. Cowles, M. Blanford, A.F. Giamei, and M.J. Bruskotter: in Proc. 7th Int. Conf. on Modeling of Casting, Welding and Advanced Solidification Processes, Minerals Metals & Materials Society, London, UK, 1995, pp. 347–54.

  9. C.J. Rosen, A. Gumenyuk, H. Zhao, and U. Dilthey: Sci. Technol. Weld. Join., 2007, vol. 12, pp. 614-619.

    Article  Google Scholar 

  10. H.Y. Zhao, P. Wang, and B. Wu: J. Tsinghua Univ. (Sic. & Technol.), 2013, vol. 53, pp. 1402–06.

  11. P.S. Wei, and W.H. Giedt (1985) Weld. J., vol. 64(9), pp. 251-259.

    Google Scholar 

  12. R. Rai, S. Kelly, R. Martukanitz (2008) Metall Mater. Trans. A, Vol. 39A, pp. 98.

    Article  Google Scholar 

  13. X. Hei, P.W. Fuerschbach, T. DebRoy (2003) J. Phys. D: Appl. Phys., Vol. 36, 1388

    Article  Google Scholar 

  14. T. Zacharia, S.A. David, J.M. Vitek, T. Debroy: Weld. J., 1989, Vol. 68, pp. 269-79

    Google Scholar 

  15. T. Liu, L.J. Yang, H.L. Wei: Weld. J., 2017, Vol. 96, pp 258-70

    Google Scholar 

  16. P.S. Wei, and Y.T. Chow: Metall. Mater. Trans. B., 1992, vol. 23, pp. 81-90.

    Article  Google Scholar 

  17. R. Rai, T.A. Palmer, and J.W. Elmer: Weld. J., 2009, vol. 88(3), pp. 54-61.

    Google Scholar 

  18. R. Rai, P. Burgradt, J.O. Milewski, and T. DebRoy (2008) J. Phys. D: Appl. Phys., vol. 42(2), p. 025503

    Article  Google Scholar 

  19. A. Lundbäck, and H. Runnemalm: Sci. Technol. Weld. Join., 2005, vol. 10, pp. 717-724.

    Article  Google Scholar 

  20. B. Huang, X. Chen, S. Pang, and R. Hu: Int. J. Heat Mass Transf., 2017, vol. 115, pp. 159-173.

    Article  Google Scholar 

  21. J. Cheon J, D.V. Kiran, S.J. Na (2016) Mater. Des., 2016, Vol. 91, pp. 230-241.

    Article  Google Scholar 

  22. M. Jamshidinia, F. Kong, R. Kovacevic: The Coupled CFD-FEM Model of Electron Beam Melting, 2013.

  23. S. Pang, X. Chen, J. Zhou, X. Shao, and C. Wang: Opt. Laser. Eng., 2015, vol. 74, pp. 47-58.

    Article  Google Scholar 

  24. S. Pang, X. Chen, X. Shao, S. Gong, and J. Xiao: Opt. Laser. Eng., 2016, vol. 82, pp. 28-40

    Article  Google Scholar 

  25. S. Pang, L. Chen, J. Zhou, Y. Yin, and T. Chen (2011) J. Phys. D Appl. Phys, vol. 44(2), p. 025301

    Article  Google Scholar 

  26. S. Osher, and J.A. Sethian (1988) J. Comput. Phys., vol. 79, pp. 12-49.

    Article  Google Scholar 

  27. R.W. Lewis, P. Nithiarasu, and K.N. Seetharamu: Fundamentals of the Finite Element Method for Heat and Fluid Flow, 1st ed., John Wiley & Sons Ltd, Chichester, 2004.

    Book  Google Scholar 

  28. A. Kermanpur, M. Shamanian, and V.E. Yeganeh: J. Mater. Process. Tech., 2008, vol. 199(1-3), pp. 295-303.

    Article  Google Scholar 

  29. Y. Ueda, and Y. Yamakaw: Trans. Jpn. Weld. Soc., 1971.

  30. Q. Tang, S. Pang, B. Chen, H. Suo, and J. Zhou (2014) Int. J. Heat Mass Transf., 2014, vol. 78, pp. 203-215.

    Article  Google Scholar 

  31. D.A. Schaue, and W.H. Geidt: Prediction of electron beam welding spiking tendency. California Univ., 1978.

  32. G.L. Mara, E.R. Funk, R.C. McMaster, and P.E. Pence (1974) Weld. J. vol. 53(6):246.

    Google Scholar 

  33. H. Tong and W.H. Giedt: Weld. J., 1970, vol. 49 (6), p. 259.

    Google Scholar 

  34. Y. Luo, J. Liu, and H. Ye: Vacuum., 2010, vol. 84(6), pp. 857-863.

    Article  Google Scholar 

  35. K. Abderrazak, S. Bannour, H. Mhiri, G. Lepalec, M.Autric: Comp. Mater. Sci., 2009, Vol. 44, pp. 858-866,

    Article  Google Scholar 

  36. X.Y. Li, L.J. Wang, L.J. Yang, J.F. Wang, K. Li: J. Mater. Process. Technol., 2014, Vol. 214, pp. 1844-1851.

    Article  Google Scholar 

  37. S. Wu, H.Y. Zhao, Y. Wang, and X.H. Zhang: Trans. China Weld. Inst., 2004, vol. 25, pp. 91-94.

    Google Scholar 

Download references

Acknowledgments

This research was supported by the Key R&D Projects (National Key projects) (Nos. 2017YFE0100100, 2018YFB1105300), the National Natural Science Foundation of China (NSFC) (No. 51675202), and the National Basic Research Program of China (973 Program, No. 2014CB046703).

Author information

Authors and Affiliations

  1. State Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology(HUST), Luoyu Rd, 1037, Wuhan, P.R. China

    Lvjie Liang

  2. State Key Laboratory of Material Processing and Die & Mould Technology, Huazhong University of Science and Technology(HUST), Luoyu Rd, 1037, Wuhan, P.R. China

    Renzhi Hu, Jingsheng Wang, Manlelan Luo, Anguo Huang & Shengyong Pang

  3. Science and Technology on Power Beam Processes Laboratory, AVIC Manufacturing Technology Institute, Beijing, P.R. China

    Bing Wu

Authors
  1. Lvjie Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Renzhi Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jingsheng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Manlelan Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Anguo Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Bing Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Shengyong Pang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shengyong Pang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Manuscript submitted August 16, 2018.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liang, L., Hu, R., Wang, J. et al. A CFD-FEM Model of Residual Stress for Electron Beam Welding Including the Weld Imperfection Effect. Metall Mater Trans A 50, 2246–2258 (2019). https://doi.org/10.1007/s11661-019-05154-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11661-019-05154-8

Search

Navigation