Riskiness in gambles that belong to the same location-scale family and with well-defined means and variances

Abstract

This paper investigates the orderings of gambles with well-defined means and variances that belong to the same location-scale family under: (i) the index of riskiness analyzed by Aumann and Serrano (AS) and (ii) the measure of riskiness proposed by Foster and Hart (FH). For both measures we study the characteristics and properties of the representation on the (mean, variance) plane of the curves that include gambles with the same level of riskiness. Our analysis applies to gambles with truncated normal distributions and beta distributions. We also discuss the relationships between different riskiness measures derived from the AS and FH measures.

Appendix

1.1 Proof of Proposition 1

i) The S-curve goes through the origin since the origin may be considered as a gamble with maximum loss of 0 and a riskiness of 0. Now consider that g is in the S-curve: $E\left[ \log \left( 1+\frac{g}{L(g)}\right) \right] =0$. Gamble h such that $\mu _{h}=\mu _{g}+\gamma$, with $0<\gamma <L(g)$, and $\sigma _{h}=\sigma _{g}$ is above gamble g on the ($\mu ,\sigma$) plane. Moreover, as $h=g+\gamma$ and $L(h)=L(g)-\gamma >0$ it emerges that $E\left[ \ln \left( 1+\frac{h}{L(h)}\right) \right] =E\left[ \log \left( 1+\frac{g+\gamma }{L(g)-\gamma }\right) \right] >E\left[ \log \left( 1+\frac{g}{L(g)}\right) \right] =0$. By contrast, if $\gamma <0$ and $-\gamma <\mu _{g}$ then $E\left[ \ln \left( 1+\frac{h}{L(h)}\right) \right] <0$. To get a gamble on the S-curve with a mean equal to $\mu _{h}$ a gamble j with standard deviation other than $\sigma _{h}$ is required, that is, a gamble j such that $\mu _{j}=\mu _{h}=\mu _{g}+\gamma$ and $\sigma _{j}=\delta \sigma _{h}=\delta \sigma _{g}$, with $\delta \ne 1$. In that case $j=\delta h+(1-\delta )\mu _{h}$, $L(j)=\delta L(h)-(1-\delta )\mu _{h}$ and it follows that:

$$\begin{aligned} E\left[ \log \left( 1+\frac{j}{L(j)}\right) \right] =E\left[ \log \left( 1+\frac{\delta h+(1-\delta )\mu _{h}}{\delta L(h)-(1-\delta )\mu _{h}}\right) \right] \end{aligned}$$

(8)

The expression in (8) is higher than $E\left[ \log \left( 1+\frac{h}{L(h)}\right) \right]$ if $\delta <1$ and lower than $E\left[ \log \left( 1+\frac{h}{L(h)}\right) \right]$ if $\delta >1$. Gamble j will also belong to the S-curve if and only if $\delta =\delta (\gamma )$ with $\delta (\gamma )$ such that:

$$\begin{aligned}&E\left[ \log \left( 1+\frac{\delta (\gamma )h+(1-\delta (\gamma ))\mu _{h}}{\delta (\gamma )L(h)-(1-\delta (\gamma ))\mu _{h}}\right) \right] =E\left[ \log \left( 1+\frac{\delta (\gamma )(g+\gamma )+(1-\delta (\gamma ))(\mu _{g} +\gamma )}{\delta (\gamma )(L(g)-\gamma )-(1-\delta (\gamma ))(\mu _{g}+\gamma )}\right) \right] \nonumber \\&\quad =E\left[ \log \left( 1+\frac{\delta (\gamma )g+\gamma +(1-\delta (\gamma ))\mu _{g}}{\delta (\gamma )L(g)-\gamma -(1-\delta (\gamma ))\mu _{g}}\right) \right] =0\text {.} \end{aligned}$$

(9)

The set of gambles belonging to the S-curve is obtained in this case from the set of values of $\gamma$ and $\delta (\gamma )$ such that $-\mu _{g}<\gamma <\delta (\gamma )L(g)-(1-\delta (\gamma ))\mu _{g}$ and (9) is fulfilled. From the foregoing it follows that if $\gamma >0$ then $\delta (\gamma )>1$ and if $\gamma <0$ then $\delta (\gamma )<1$. As a consequence, the S-curve is increasing.

ii) In i) it is shown that $E\left[ \log \left( 1+\frac{g}{L(g)}\right) \right]$ decreases when the mean of the gamble decreases and its standard deviation remains unchanged. This implies that part A of iso-$R^{FH}$-riskiness V lies on the ($\mu ,\sigma$) plane below the S-curve as $E\left[ \log \left( 1+\frac{g}{L(g)}\right) \right] <0$ for gambles in that part of iso-$R^{FH}$-riskiness V. Moreover, part B of iso-$R^{FH}$-riskiness V lies on the ($\mu ,\sigma$) plane above (and on) the S-curve as $E\left[ \log \left( 1+\frac{g}{L(g)}\right) \right] \ge 0$ for gambles in that part of iso-$R^{FH}$-riskiness V.

iii) The indifference curve through the origin of a decision maker with a logarithmic utility and wealth V runs towards the straight line $\mu =\tilde{L}\sigma -V$ without reaching that line, because that indifference curve is defined only for gambles with maximum losses lower than V. The point on the straight line $\mu =\tilde{L}\sigma -V$ that belongs to the frontier of that indifference curve is the intercept point between the S-curve and the straight line $\mu =\tilde{L}\sigma -V$, as at that point the maximum loss is V and, hence, FH-riskiness is equal to V. That intercept point belongs to part B of iso-$R^{FH}$-riskiness V, so it follows that each iso-$R^{FH}$-riskiness is continuous on the ($\mu ,\sigma$) plane. $\square$

1.2 Proof of Proposition 2

From $\left[ RiH\right]$ it follows that for a beta-distributed gamble g with shape parameters $\alpha$ and $\beta$: $E\left[ \log \left( 1+\frac{g}{L(g)}\right) \right] =0\Leftrightarrow \log (M(g)+L(g))+E\log Z=\log (L(g))$, where Z is the gamble beta-distributed between 0 and 1 with shape parameters $\alpha$ and $\beta$. It emerges that:

$$\begin{aligned}&\log (M(g)+L(g))+E\log Z=\log (L(g))\Leftrightarrow \log \left( \frac{M(g)+L(g)}{L(g)}\right) =-E\log Z\\&\quad \Leftrightarrow \log \left( \frac{(\alpha +\beta )\kappa \sigma _{g}}{\alpha \kappa \sigma _{g}-\mu _{g}}\right) =-E\log Z\Leftrightarrow \frac{(\alpha +\beta )\kappa \sigma _{g}}{\alpha \kappa \sigma _{g}-\mu _{g}}=e^{-E\log Z}\\&\quad \Leftrightarrow \mu _{g}=\kappa \sigma _{g}\left( \alpha -\frac{\alpha +\beta }{e^{-E\log Z}}\right) \end{aligned}$$

Hence, for beta-distributed gambles with shape parameters $\alpha$ and $\beta$ the S-curve on the ($\mu ,\sigma$) plane is the straight line $\mu =\kappa \sigma (\alpha -\frac{\alpha +\beta }{e^{-E\log Z}})$. Taking into account the pdf of a beta distribution between 0 and 1 with shape parameters $\alpha$ and $\beta$ it follows that:

$$\begin{aligned} E\log Z=\int _{0}^{1}\frac{(x)^{\alpha -1}(1-x)^{\beta -1}\log x}{\int _{0} ^{1}(x)^{\alpha -1}(1-x)^{\beta -1}dx}dx\text {.} \end{aligned}$$

$\blacksquare$

1.3 Comparison of iso-$R^{AS}$-riskiness and iso-$R^{FH}$-riskiness curves in gambles with uniform distributions: Analysis and simulations

From the analysis in Section 3.2 it follows that for any gamble g belonging to part A of iso-$R^{FH}$-riskiness V it is required that $\mu _{g} -\sqrt{3}\sigma _{g}>-V$. Moreover, part A of that iso-$R^{FH}$-riskiness may be written as $E\left[ \log (V+g)\right] =\log V$. Since $\int \log (V+x)dx=(V+x)\log \left( V+x\right) -x-V\log (\frac{1}{V})$, it follows that:

$$\begin{aligned}&E\left[ \log (V+g)\right] \nonumber \\&\quad =\int _{\mu -\sqrt{3}\sigma }^{\mu +\sqrt{3}\sigma } \log (V+x)\frac{1}{2\sqrt{3}\sigma }dx\nonumber \\&\quad =\frac{(\mu +\sqrt{3}\sigma +V)\log (\mu +\sqrt{3}\sigma +V)-(\mu -\sqrt{3} \sigma +V)\log (\mu -\sqrt{3}\sigma +V)-2\sqrt{3}\sigma }{2\sqrt{3}\sigma }\nonumber \\ \end{aligned}$$

(10)

From (10) it emerges that the slope at point ($\mu ,\sigma$) in part A of iso-$R^{FH}$-riskiness V is:

$$\begin{aligned} \frac{d\mu }{d\sigma }&=\frac{\left( \mu +V\right) \left[ \log \left( V+\mu +\sqrt{3}\sigma \right) -\log \left( V+\mu -\sqrt{3}\sigma \right) \right] -2\sqrt{3}\sigma }{\sigma \left[ \log \left( V+\mu +\sqrt{3} \sigma \right) -\log \left( V+\mu -\sqrt{3}\sigma \right) \right] }\nonumber \\&\quad =\frac{\mu +V}{\sigma }-\frac{2\sqrt{3}}{\log \left( V+\mu +\sqrt{3} \sigma \right) -\log \left( V+\mu -\sqrt{3}\sigma \right) }\text {.} \end{aligned}$$

(11)

Hence, it follows from (11) that:

$$\begin{aligned}&\lim _{\mu \rightarrow \sqrt{3}\sigma -V}\left( \frac{d\mu }{d\sigma }\right) \\&\quad =\lim _{\mu \rightarrow \sqrt{3}\sigma -V}\left( \frac{\left( \mu +V\right) (\log \left( V+\mu +\sqrt{3}\sigma \right) -\log \left( V+\mu -\sqrt{3} \sigma \right) )-2\sqrt{3}\sigma }{\sigma \left( \log \left( V+\mu +\sqrt{3} \sigma \right) -\log \left( V+\mu -\sqrt{3}\sigma \right) \right) }\right) =\sqrt{3}\text {.} \end{aligned}$$

Since part A of any iso-$R^{FH}$-riskiness is increasing and convex, it can be concluded that the slope at any point in part A of an iso-$R^{FH}$-riskiness is lower than $\sqrt{3}$.

From (10) it can also be proved that ($\mu =(\frac{e}{2}-1)V=0.359V,\sigma =\frac{eV}{2\sqrt{3}}=0.785V$) is the intercept point between the S-curve and the straight line $\mu =\sqrt{3}\sigma -V$ that belongs to the frontier of part A of iso-$R^{FH}$-riskiness V, a result already obtained in Section 5.2, since it follows that:

$$\begin{aligned}&\lim _{\mu \rightarrow \sqrt{3}\sigma -V}\frac{(\mu +\sqrt{3}\sigma +V)\log (\mu +\sqrt{3}\sigma +V)-(\mu -\sqrt{3}\sigma +V)\log (\mu -\sqrt{3}\sigma +V)-2\sqrt{3}\sigma }{2\sqrt{3}\sigma }\\&\quad =\frac{1}{2\sqrt{3}\sigma }\left[ 2\sqrt{3}\sigma \log (2\sqrt{3}\sigma )-2\sqrt{3}\sigma \right] =\log (V)\text {.} \end{aligned}$$

Hence, at that limiting point it is:

$$\begin{aligned} \frac{2\sqrt{3}\sigma }{e}=V\Leftrightarrow \sigma =\frac{eV}{2\sqrt{3}}=0.785V \end{aligned}$$

and $\mu =(\frac{e}{2}-1)V=0.359V$.

We now study the positions of the iso-$R^{AS}$-riskiness curves with respect to the iso-$R^{FH}$-riskiness V. Using (5) to substitute $\mu$ from the iso-AS-riskiness $\frac{1}{a}$ into part A of the iso-$R^{FH}$-riskiness V it follows from (10) and from $E\left[ \log (V+g)\right] =\log V$ that:

$$\begin{aligned}&\left( -\sqrt{3}\sigma +\frac{1}{a}\log \left( \frac{-1+e^{2a\sigma \sqrt{3}} }{2a\sigma \sqrt{3}}\right) +\sqrt{3}\sigma +V\right) \\&\qquad \times \log \left( -\sqrt{3}\sigma +\frac{1}{a}\log \left( \frac{-1+e^{2a\sigma \sqrt{3}}}{2a\sigma \sqrt{3}}\right) +\sqrt{3}\sigma +V\right) \\&\qquad -\left( -\sqrt{3}\sigma +\frac{1}{a}\log \left( \frac{-1+e^{2a\sigma \sqrt{3}} }{2a\sigma \sqrt{3}}\right) -\sqrt{3}\sigma +V\right) \\&\qquad \times \log \left( -\sqrt{3}\sigma +\frac{1}{a}\log \left( \frac{-1+e^{2a\sigma \sqrt{3}}}{2a\sigma \sqrt{3}}\right) -\sqrt{3}\sigma +V\right) \\&\qquad -2\sqrt{3}\sigma =2\sqrt{3}\sigma \log (V) \end{aligned}$$

Let:

$$\begin{aligned}&G(V,a,\sigma )\equiv \left( \frac{1}{a}\log \left( \frac{-1+e^{2a\sigma \sqrt{3}} }{2a\sigma \sqrt{3}}\right) +V\right) \log \left( \frac{1}{a}\log \left( \frac{-1+e^{2a\sigma \sqrt{3}}}{2a\sigma \sqrt{3}}\right) +V\right) \\&\qquad -\left( \frac{1}{a}\log \left( \frac{-1+e^{2a\sigma \sqrt{3}}}{2a\sigma \sqrt{3} }\right) -2\sqrt{3}\sigma +V\right) \log \left( \frac{1}{a}\log \left( \frac{-1+e^{2a\sigma \sqrt{3}}}{2a\sigma \sqrt{3}}\right) -2\sqrt{3}\sigma +V\right) \\&\qquad -2\sqrt{3}\sigma (1+\log (V)) \end{aligned}$$

The sign of $G(V,a,\sigma )$ must be studied to check the positions of the iso-$R^{AS}$-riskiness curves with respect to part A of the iso-$R^{FH}$-riskiness V. If $G(V,a,\sigma )>0$ ($<0$) then the iso-AS-riskiness $\frac{1}{a}$ is above (below) part A the iso-$R^{FH}$-riskiness V for that level of $\sigma$. Simulations are used below to show that all iso-$R^{AS}$-riskiness curves with levels of riskiness higher than V are below the iso-$R^{FH}$-riskiness V (except at the origin) and that all iso-$R^{AS}$-riskiness curves with levels of riskiness lower than V are above part A of the iso-$R^{FH}$-riskiness V or intercept it from above.

Consider the iso-$R^{FH}$-riskiness 1 (the results would be similar for any other iso-$R^{FH}$-riskiness). Part A of that iso-$R^{FH}$-riskiness is defined for $0<\sigma <0.785$. Moreover, if $a=1$ then:

$$\begin{aligned} G(1,1,\sigma )= & {} \left( \log \left( \frac{-1+e^{2\sigma \sqrt{3}}}{2\sigma \sqrt{3} }\right) +1\right) \log \left( \log \left( \frac{-1+e^{2\sigma \sqrt{3}}}{2\sigma \sqrt{3} }\right) +1\right) \\&-\left( \log \left( \frac{-1+e^{2\sigma \sqrt{3}}}{2\sigma \sqrt{3}}\right) -2\sqrt{3}\sigma +1\right) \\&\quad \times \log \left( \log \left( \frac{-1+e^{2\sigma \sqrt{3}}}{2\sigma \sqrt{3}}\right) -2\sqrt{3}\sigma +1\right) -2\sqrt{3}\sigma \end{aligned}$$

Giving values of between 0 and 0.785 to $\sigma$ it is obtained that $G(1,1,0)=0$ and that $G(1,1,\sigma )$ decreases with $\sigma$. Hence, all iso-$R^{AS}$-riskiness with levels of AS-riskiness of 1 or more are below iso-$R^{FH}$-riskiness 1.

At the iso-$R^{AS}$-riskiness curve that goes through the point ($\mu =0.359,\sigma =0.785$) it follows from Section 5 that:

$$\begin{aligned} \frac{1}{2\sqrt{3}a\sigma }(e^{a(\sqrt{3}\sigma -\mu )}-e^{-a(\sqrt{3}\sigma +\mu )})=1\Rightarrow a=1.274 \end{aligned}$$

Hence, the iso-$R^{AS}$-riskiness curve that runs through the point ($\mu =0.359,\sigma =0.785$) is the iso-$R^{AS}$-riskiness $\frac{1}{1.274}$. The curvature at the origin of that iso-$R^{AS}$-riskiness (1.274) is greater than the curvature at the origin (1) of the iso-$R^{FH}$-riskiness 1. Hence, that iso-$R^{AS}$-riskiness $\frac{1}{1.274}$ is above iso-$R^{FH}$-riskiness 1 at least for small values of $\sigma$ .¹² It emerges that:

$$\begin{aligned} G(1,1.274,\sigma )= & {} \left( \frac{1}{1.274}\log \left( \frac{-1+e^{2(1.274)\sigma \sqrt{3}}}{2(1.274)\sigma \sqrt{3}}\right) +1\right) \\&\times \log \left( \frac{1}{1.274}\log \left( \frac{-1+e^{2(1.274)\sigma \sqrt{3}}}{2(1.274)\sigma \sqrt{3}}\right) +1\right) \\&-\left( \frac{1}{1.274}\log \left( \frac{-1+e^{2(1.274)\sigma \sqrt{3}} }{2(1.274)\sigma \sqrt{3}}\right) -2\sqrt{3}\sigma +1\right) \\&\times \log \left( \frac{1}{1.274} \log \left( \frac{-1+e^{2(1.274)\sigma \sqrt{3}}}{2(1.274)\sigma \sqrt{3}}\right) \right. \\&-2\sqrt{3}\sigma +1)-2\sqrt{3}\sigma \end{aligned}$$

Giving values of between 0 and 0.785 to $\sigma$ it is obtained that $G(1,1.274,\sigma )>0$ (and that $G(1,1.274,\sigma )$ increases for $\sigma <0.6725$ and decreases for $\sigma >0.6725$). Hence, all iso-$R^{AS}$-riskiness with levels of AS-riskiness of $\frac{1}{1.274}$ or less are above part A of iso-$R^{FH}$-riskiness 1. However, those iso-$R^{AS}$-riskiness will intercept part B of iso-$R^{FH}$-riskiness 1 from above because the slope of any iso-$R^{AS}$-riskiness curve is lower than $\sqrt{3}$ for any $\sigma$ (and $\sqrt{3}$ is the slope for any $\sigma$ in part B of any iso-$R^{FH}$-riskiness curve).

Finally, consider any iso-$R^{AS}$-riskiness with a level of AS-riskiness between $\frac{1}{1.274}$ and 1. From Sections 3.1 and 3.2 it is known that the first derivatives of all iso-$R^{AS}$-riskiness curves and of all iso-$R^{FH}$-riskiness curves at the origin are 0 and that the second derivatives at the origin of iso-$R^{AS}$-riskiness V and of iso-$R^{FH}$-riskiness V are $\frac{1}{V}$. Hence, all iso-$R^{AS}$-riskiness curves with levels of riskiness lower than 1 are above the iso-$R^{FH}$-riskiness 1 at least for low values of $\sigma$. Moreover, from the previous paragraph it follows that all iso-$R^{AS}$-riskiness curves with levels of riskiness higher than $\frac{1}{1.274}$ are below part A of iso-$R^{FH}$-riskiness 1 at least for values of $\sigma$ a little lower than 0.785. It can be concluded that any iso-$R^{AS}$-riskiness with a level of AS-riskiness between $\frac{1}{1.274}$ and 1 will intercept part A of iso-$R^{FH}$-riskiness 1.

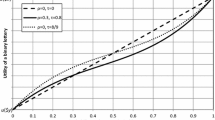
All simulations show that an iso-$R^{AS}$-riskiness with level of AS-riskiness between $\frac{1}{1.274}$ and 1 intercepts iso-$R^{FH}$-riskiness 1 only once and that any of such iso-$R^{AS}$-riskiness intercepts part A of iso-$R^{FH}$-riskiness 1 from above. Hence, for an iso-$R^{AS}$-riskiness V with $\frac{1}{1.274}<V<1$ it is obtained that $G(1,V,\sigma )>0$ ($<0$) for $\sigma$ higher (lower) than the value of $\sigma$ such that $G(1,V,\sigma )=0$. For instance, if $V=\frac{1}{1.2}=0.833\,33$ then $G(1,0.8333,\sigma )=0\Rightarrow \sigma =0.7271$ and if $V=\frac{1}{1.1}=0.909\,09$ then $G(1,0.909,\sigma )=0\Rightarrow \sigma =0.5697$. As expected $\sigma$ decreases at the intercept point between an iso-$R^{AS}$-riskiness and iso-$R^{FH}$-riskiness 1 when the level of AS-riskiness of that iso-$R^{AS}$-riskiness increases. $\blacksquare$