Abstract
Maximum drawdown, the largest cumulative loss from peak to trough, is one of the most widely used indicators of risk in the fund management industry, but one of the least developed in the context of measures of risk. We formalize drawdown risk as Conditional Expected Drawdown (CED), which is the tail mean of maximum drawdown distributions. We show that CED is a degree one positive homogenous risk measure, so that it can be linearly attributed to factors; and convex, so that it can be used in quantitative optimization. We empirically explore the differences in risk attributions based on CED, Expected Shortfall (ES) and volatility. An important feature of CED is its sensitivity to serial correlation. In an empirical study that fits AR(1) models to US Equity and US Bonds, we find substantially higher correlation between the autoregressive parameter and CED than with ES or with volatility.








Similar content being viewed by others
Notes
See [25] for an analysis of the flash crash.
The track record is understood as the length of the history of an investment fund since its inception.
Another crucial ingredient is having a reliable risk model feeding the optimizer with realistic and useful scenarios. This being beyond the scope of the present article, we have focused on the two main theoretical requirements in the present article. We refer the reader to [42], where the theory of risk estimation and error sensitivity in the context of portfolio optimization is discussed.
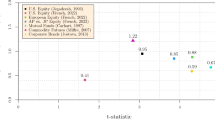
This formula and the topic of risk attribution is discussed in more detail in Sect. 4.
The process corresponding to the i-th factor is written \(F_i\), and its instance at time \(t\in [0,T]\) is denoted by \(F_{i,t}\).
See Appendix A for details on the data and their source.
We thank Robert Anderson for pointing out the important distinction between US Government Bond and US Treasury Bond Indices.
See Appendix B for details on the risk estimation and portfolio construction methodologies used. Note also that similar effects can be seen in other fixed-mix portfolios, such as the equal-weighted 50/50 portfolio and the 70/30 allocation. In the following empirical analyses, we will be focusing exclusively on the traditional 60/40 allocation.
For comparison, we include in Fig. 11 of Appendix C the risk decomposition along expected shortfall.
See Appendix B for details on the data, risk estimation, and portfolio construction methodologies used.
See for example [27].
References
Acerbi, C., Tasche, D.: Expected shortfall: a natural coherent alternative to value at risk. Econ. Notes 31(2), 379–388 (2002a)
Acerbi, C., Tasche, D.: On the coherence of expected shortfall. J. Bank. Financ. 26(7), 1487–1503 (2002b)
Anderson, R.M., Bianchi, S.W., Goldberg, L.R.: Will my risk parity strategy outperform? Financ. Anal. J. 68(6), 75–93 (2012)
Anderson, R,M., Bianchi, S.W., Goldberg, L.R.: Determinants of levered portfolio performance. Forthcom. Financ. Anal. J. (2014)
Bertsimas, D., Lauprete, G.J., Samarov, A.: Shortfall as a risk measure: properties, optimization and applications. J. Econ. Dyn. Control 28, 1353–1381 (2004)
Burghardt, G., Duncan, R., Liu, L.: Deciphering drawdown. Risk Mag. 16–20 (2003)
Carr, P., Zhang, H., Hadjiliadis, O.: Maximum drawdown insurance. Int. J. Theor. Appl. Financ. 14, 1195–1230 (2011)
Chekhlov, A., Uryasev, S., Zabarankin, M.: Portfolio optimization with drawdown constraints. In: Scherer, B. (ed.) Asset and Liability Management Tools, pp. 263–278. Risk Books, London (2003)
Chekhlov, A., Uryasev, S., Zabarankin, M.: Drawdown measure in portfolio optimization. Int. J. Theor. Appl. Financ. 8(1), 13–58 (2005)
Cheridito, P., Delbaen, F., Kupper, M.: Coherent and convex monetary risk measures for bounded càdlàg processes. Stoch. Process. Appl. 112, 1–22 (2004)
Cherney, V., Obloj, J.: Portfolio optimization under non-linear drawdown constraints in a semimartingale financial model. Financ. Stochastics 17, 771–800 (2013)
Cvitanic, J., Karatzas, I.: On portfolio optimization under drawdown constraints. IMA Lect. Notes Math. Appl. 65, 77–88 (1995)
Denault, M.: Coherent allocation of risk capital. J. Risk 4(1), 7–21 (2001)
Douady, R., Shiryaev, A.N., Yor, M.: On probability characteristics of downfalls in a standard brownian motion. Theory Probab. Appl. 44, 29–38 (2000)
Föllmer, H., Schied, A.: Convex measures of risk and trading constraints. Financ. Stoch. 6, 429–447 (2002)
Föllmer, H., Schied, A.: Coherent and convex risk measures. In: Cont, R. (ed) Encyclopedia of Quantitative Finance, pp. 355–363. Wiley, New York (2010)
Föllmer, H., Schied, A.: Stochastic Finance: An Introduction in Discrete Time. Walter de Gruyter, Berlin (2011)
Goldberg, L.R., Menchero, J., Hayes, M., Mitra, I.: Extreme risk analysis. J. Perform. Meas. 14(3), 17–30 (2010)
Grossman, S.J., Zhou, Z.: Optimal investment strategies for controlling drawdowns. Math. Financ. 3, 241–276 (1993)
Hadjiliadis, O., Vecer, J.: Drawdowns preceding rallies in the brownian motion model. Quant Financ. 6, 403–409 (2006)
Kalkbrener, M.: An axiomatic approach to capital allocation. Math. Financ. 15(3), 425–437 (2005)
Krokhmal, P., Uryasev, S., Zrazhevsky, G.: Numerical comparison of cvar and cdar approaches: application to hedge funds. In: Ziemba, W.T. (ed.) The stochastic programming approach to asset liability and wealth management. AIMR/Blackwell Publisher, Oxford (2003)
Landriault, D., Li, B., Zhang, H.: On the frequency of drawdowns for brownian motion processes. J. Appl. Probab. 52(1), 191–208 (2015)
Lehoczky, J.P.: Formulas for stopped diffusion processes with stopping times based on the maximum. Ann. Probab. 5, 601–607 (1977)
Madhavan, A.: Exchange-traded funds, market structure, and the flash crash. Financ. Anal. J. 68(4), 20–35 (2012)
Magdon-Ismail, M., Atiya, A.F., Pratap, A., Abu-Mostafa, Y.: On the maximum drawdown of a brownian motion. J. Appl. Probab. 41, 147–161 (2004)
McNeil, A.J., Frey, R., Embrechts, P.: Quantitative Risk Management: Concepts, Techniques, and Tools. Princeton University Press, Princeton (2005)
Menchero, J., Poduri, V.: Custom factor attribution. Financ. Anal. J. 64(2), 81–92 (2008)
Mijatovic, A., Pistorius, M.R.: On the drawdown of completely asymmetric lévy processes. Stoch. Process. Appl. 122, 3812–3836 (2012)
Pospisil, L., Vecer, J.: Portfolio sensitivity to changes in the maximum and the maximum drawdown. Quant. Financ. 10, 617–627 (2010)
Pospisil, L., Vecer, J., Hadjiliadis, O.: Formulas for stopped diffusion processes with stopping times based on drawdowns and drawups. Stoch. Process. Appl. 119, 2563–2578 (2009)
Qian, E.: On the financial interpretation of risk contributions: risk budgets do add up. J. Invest. Manag. 4(4), 41–51 (2006)
Rockafellar, R.T., Uryasev, S.: Optimization of conditional value-at-risk. J. Risk 2, 21–41 (2000)
Rockafellar, R.T., Uryasev, S.: Conditional value-at-risk for general loss distributions. J. Bank. Financ. 26, 1443–1471 (2002)
Rockafellar, R.T., Uryasev, S.P., Zabarankin, M.: Deviation measures in risk analysis and optimization. Technical report, University of Florida, Department of Industrial and Systems Engineering (2002)
Rockafellar, R.T., Uryasev, S.P., Zabarankin, M.: Generalized deviations in risk analysis. Financ. Stoch. 10(1), 51–74 (2006)
Sekine, J.: Long-term optimal investment with a generalized drawdown constraint. SIAM J. Financ. Math. 4, 457–473 (2013)
Tasche, D.: Risk contributions and performance measurement. Technical report, Research paper, Zentrum Mathematik (SCA) (2000)
Tasche, D.: Expected shortfall and beyond. J. Bank. Financ. 26, 1519–1533 (2002)
Taylor, H.M.: A stopped brownian motion formula. Ann. Probab. 3, 234–246 (1975)
Zabarankin, M., Pavlikov, K., Uryasev, S.: Capital asset pricing model (capm) with drawdown measure. Eur. J. Oper. Res. 234, 508–517 (2014)
Zabarankin, M., Uryasev, S.: Statistical Decision Problems: Selected Concepts and Portfolio Safeguard Case Studies, vol. 85. Springer, Berlin (2014)
Zhang, H.: Occupation time, drawdowns, and drawups for one-dimensional regular diffusion. Adv. Appl. Probab., 47(1), 210–230 (2015)
Zhang, H., Hadjiliadis, O.: Drawdowns and rallies in a finite time-horizon. Methodol. Comput. Appl. Probab. 12, 293–308 (2010)
Zhang, H., Leung, T., Hadjiliadis, O.: Stochastic modeling and fair valuation of drawdown insurance. Insur. Math. Econ. 53, 840–850 (2013)
Author information
Authors and Affiliations
Corresponding author
Additional information
We are grateful to Robert Anderson for insightful comments on the material discussed in this article; to Alexei Chekhlov, Stan Uryasev, and Michael Zabarankin for their feedback on a previous draft of this work; to Vladislav Dubikovsky, Michael Hayes, and Márk Horváth for their contributions to an earlier version of this article; to Carlo Acerbi for providing detailed comments on a previous draft; and to the referees and editors of Mathematics and Financial Economics for their valuable feedback.
Appendices
Appendix A: Data and estimation methodologies
1.1 Data
The data were obtained from the Global Financial Data database. We took the daily time series for the S&P 500 Index and the USA 10-year Government Bond Total Return Index.
1.2 Portfolio construction
Rather than provide thorough realistic empirical analyses of portfolio risk and return, our goal behind the simulated portfolios is to illustrate this article’s theoretical development in relation to drawdown risk. For simplicity, we therefore do not account for transaction costs or market frictions in all hypothetical portfolios constructed throughout this study. Moreover, we assume that all portfolios are fully invested and long only.
Fixed-mix portfolios. In the fixed-mix portfolios, rebalancing to the fixed weights is done on a monthly basis. When comparing to other popular rebalancing schemes (quarterly, bi-annually and yearly), similar results were obtained.
Risk parity portfolios. In risk parity strategies, assets are weighted so their ex post risk contributions are equal. As mentioned in Sect. 5, parity portfolios are not restricted to volatility only, but can be constructed along other risk measures, such as Expected Shortfall and Conditional Expected Drawdown. Asset weights in the strategies depend on estimates of the underlying risk measures (see Sect. A.3), which are calculated using a 3-year rolling window of trailing returns. Varying the estimation methodology by changing the length of the rolling window or the weighting scheme applied to the returns within this window did not alter our results substantially. Similar to the fixed-mix portfolios, risk parity portfolios are rebalanced monthly, with other rebelancing schemes yielding similar results.
1.3 Risk estimation
Volatility. Portfolio volatility is calculated as the annualized standard deviation of the daily time series over the entire period under consideration. To obtain the volatility risk contributions for a n-asset portfolio \(P = \sum _i w_i X_i\), note that the i-th total contribution \(\mathrm{RC}_i^\sigma \) to portfolio volatility
is
where \(\sigma _i^2\) is the variance of \(X_i\) and \(\sigma _{i,j}\) is the covariance of \(X_i\) and \(X_j\). Then, the i-th fractional contribution to volatility is given by
Expected shortfall. For confidence level \(\alpha \in (0,1)\), an estimate for the Expected Shortfall of a portfolio is calculated by ordering the daily return time series over the whole period according to the magnitude of the returns, then averaging over the worst \((1-\alpha )\) percent outcomes, more specifically:
where T is the length of the daily time series, \(K = \lfloor T(1-\alpha ) \rfloor \), and \(r_{(i)}\) is the i-th return of the magnitude-ordered time series. To obtain the contributions to shortfall risk, recall that under a continuity assumption, the Expected Shortfall of an asset \(X \in {\mathcal {M}}\) can be expressed as \(\mathrm{ES}_\alpha (X) = {\mathbb {E}}\left( X \mid X \ge \mathrm{VaR}_\alpha (X)\right) \), or the expected loss in the event that its Value-at-Risk at \(\alpha \) is exceeded.Footnote 14 As usual, let \(P = \sum _i w_i X_i\) be the portfolio in consideration. Assuming differentiability of the risk measure VaR, the marginal contribution of \(X_i\) to portfolio shortfall \(\mathrm{ES}_\alpha (P)\) is given by
An estimate for the i-th marginal contribution to shortfall risk is then obtained by averaging over all the returns of asset \(X_i\) that coincide with portfolio returns exceeding the portfolio’s Value-at-Risk at threshold \(\alpha \).
Conditional expected drawdown. The first step in calculating an estimate for Conditional Expected Drawdown is to obtain the empirical maximum drawdown distribution. From the historical time series of returns, we generate return paths of fixed length n using a one-day rolling window. This means that consecutive paths overlap. The advantage is that for a return time series of length T, we obtain a maximum drawdown series of length \(T-n\), which for large T and small n is fairly large, too. From these \(T-n\) return paths we calculate the maximum drawdown as defined in Sect. 2. An estimate for the Conditional Expected Drawdown at confidence level \(\alpha \in (0,1)\) is then calculated as the average of the largest \((1-\alpha )\) percent maximum drawdowns. To obtain an estimate for the i-th contribution to drawdown risk CED, we take the average over all the drawdowns of the i-th asset in the path \([t_{j*},t_{k*}]\) that coincide with the overall portfolio’s maximum drawdowns that exceed the portfolio’s drawdown threshold \(\text {DT}_\alpha \) at confidence level \(\alpha \) (Recall that \(j^*<k^*\le n\) are such that \( \varvec{\mu }(P_{T_n}) = P_{t_{k*}} - P_{t_{j*}}. \))
Appendix B: Drawdown risk decomposition along a balanced portfolio of US Equity and US treasury bonds
Daily 6-month rolling fractional risk contributions (FRC) along 90 % conditional expected drawdown (CED) of US Equity and US Treasury Bonds to the balanced 60/40 portfolio over the period 1982–2013. Also displayed is the daily VIX series over the same period, with the right-hand axis indicating its level
Decomposition of drawdown risk contributions \( \mathrm{RC}^\mathrm {CED}_i(P) = w_i \mathrm {CED}(X_i) \mathrm Corr^\mathrm {CED}_i\) for the 60/40 allocation to US Equity and US Treasury Bonds over the period 1982–2013. The top two panels show the daily 6-month rolling standalone 90 % Conditional Expected Drawdown (CED) of the two assets, while the bottom two panels show the 6-month rolling generalized correlations of the individual assets along CED
Appendix C: Risk decomposition along expected shortfall
See Fig. 11.
Rights and permissions
About this article
Cite this article
Goldberg, L.R., Mahmoud, O. Drawdown: from practice to theory and back again. Math Finan Econ 11, 275–297 (2017). https://doi.org/10.1007/s11579-016-0181-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11579-016-0181-9