A Stochastic Model for Reproductive Isolation Under Asymmetrical Mating Preferences

Abstract

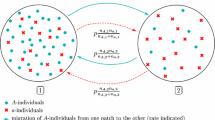
More and more evidence shows that mating preference is a mechanism that may lead to a reproductive isolation event. In this paper, a haploid population living on two patches linked by migration is considered. Individuals are ecologically and demographically neutral on the space and differ only on a trait, a or A, affecting both mating success and migration rate. The special feature of this paper is to assume that the strengths of the mating preference and the migration depend on the trait carried. Indeed, patterns of mating preferences are generally asymmetrical between the subspecies of a population. I prove that mating preference interacting with frequency-dependent migration behavior can lead to a reproductive isolation. Then, I describe the time before reproductive isolation occurs. To reach this result, I use an original method to study the limiting dynamical system, analyzing first the system without migration and adding migration with a perturbation method. Finally, I study how the time before reproductive isolation is influenced by the parameters of migration and of mating preferences, highlighting that large migration rates tend to favor types with weak mating preferences.

Appendices

Appendix A: Dynamical System Without Migration

In this appendix, we will prove the results of Sect. 3.2, which is related to the case without migration. To this aim, we use the two following weighted quantities

$$\begin{aligned}&\varOmega (t):=(\beta _A-1)z_A(t)-(\beta _a-1)z_a(t), \\&\varSigma (t):=(\beta _A-1)z_A(t)+(\beta _a-1)z_a(t). \end{aligned}$$

From (12), we find that

$$\begin{aligned} \frac{{\hbox {d}}}{{\hbox {d}}t}\varOmega (t)= & {} \varOmega \left[ b\dfrac{\beta _Az_A+\beta _a z_a}{z_A+z_a}-d-c(z_A+z_a) \right] , \end{aligned}$$

(23)

$$\begin{aligned} \frac{{\hbox {d}}}{{\hbox {d}}t}\varSigma (t)= & {} \varSigma \left[ b\dfrac{\beta _Az_A+\beta _a z_a}{z_A+z_a}-d-c(z_A+z_a) \right] \nonumber \\&-\,2b(\beta _A-1)(\beta _a-1)\dfrac{z_az_A}{z_A+z_a}. \end{aligned}$$

(24)

Proof of Lemma 3

We start by studying the stability of equilibrium (0, 0). Assume that $\varSigma (0)>0$. From (24), we derive

$$\begin{aligned} \frac{{\hbox {d}}}{{\hbox {d}}t}\varSigma \ge \varSigma \left[ b-d +b\left( \frac{\varSigma }{z_A+z_a}-2(\beta _A-1)(\beta _a-1)\frac{z_az_A}{(z_A+z_a)\varSigma } \right) -c(z_A+z_a)\right] . \end{aligned}$$

Since $\varSigma ^2-2(\beta _A-1)(\beta _a-1)z_az_A \ge 0$ and $-(\beta _{\min }-1)(z_A+z_a) \ge -\varSigma$, we deduce that

$$\begin{aligned} \frac{{\hbox {d}}}{{\hbox {d}}t}\varSigma \ge \varSigma \left[ b-d -c\frac{\varSigma }{(\beta _{\min }-1)}\right] . \end{aligned}$$

Hence, as long as $\varSigma \in ]0,(b-d)(\beta _{\min }-1)/c[$, $\varSigma (t)$ is increasing. Thus (0, 0) is an unstable equilibrium.

The stability of the three other equilibria, $(\zeta _A,0)$, $(0,\zeta _a)$ and $(\chi _A,\chi _a)$, can be deduce by a direct computation of Jacobian matrices at these points, which we do not detail.

Finally, let us study the long-time behavior of any solution. Equation (23) implies that the sign of $\varOmega (t)$ is equal at all time and, that ${\mathcal {D}}^A_0$ is a positively invariant set under dynamical system (12). Moreover, there exists only a stable equilibrium that belongs to the set ${\mathcal {D}}^A_0$, which is $(\zeta _A,0)$.

We consider the function $W: {\mathcal {D}}^A_0 \rightarrow \mathbb {R}$:

$$\begin{aligned} W(z_A,z_a):=\ln \left( \dfrac{\varSigma }{\varOmega } \right) =\ln \left( \dfrac{(\beta _A-1)z_A+(\beta _a-1)z_a}{(\beta _A-1)z_A-(\beta _a-1)z_a}\right) \ge 0 . \end{aligned}$$

(25)

From (23) and (24), we deduce that

$$\begin{aligned} \dfrac{{\hbox {d}}W(z_A(t),z_a(t))}{{\hbox {d}}t}= -2b(\beta _A-1)(\beta _a-1)\dfrac{z_az_A}{(z_A+z_a)\varSigma } \le 0 . \end{aligned}$$

Moreover for any $(z_A,z_a)\in {\mathcal {D}}^A_0$, $W(z_A,z_a)=0$ if and only if $z_a=0$. $W(z_A,z_a)$ converges to $+\,\infty$ when $(\beta _A-1)z_A-(\beta _a-1)z_a$ converges to 0 and $\frac{dW}{dt}$ is non-positive on ${\mathcal {D}}^A_0$ and is equal to zero if and only if $z_a=0$. It ensures that W is a Lyapunov function for (12) on the set ${\mathcal {D}}^A_0$ which cancels only on ${\mathcal {D}}^A_0 \cap \{z_a=0\}$. Furthermore, a simple computation gives that the largest invariant set in ${\mathcal {D}}^A_0 \cap \{z_a=0\}$ is $\{(\zeta _A,0)\}$. Theorem 1 of LaSalle (1960) is thus sufficient to conclude that any solution of (12) with initial condition in ${\mathcal {D}}^A_0$ converges to $(\zeta _A,0)$ when t tends to $+\,\infty$. Similarly, we prove that any solution with initial condition in ${\mathcal {D}}^a_0$ converges to $(0,\zeta _a)$.

Finally, assume that $\varOmega (0)=0$. Then, $\varOmega (t)=0$ for all $t\ge 0$ according to (23) and, in addition with (12), we derive for all $\alpha \in \mathcal {A}$,

$$\begin{aligned} \dfrac{{\hbox {d}}}{{\hbox {d}}t}z_\alpha =z_\alpha \left[ b\frac{\beta _A\beta _a-1}{\beta _A+\beta _a-2}-d-c\frac{\beta _A+\beta _a-2}{\beta _{\bar{\alpha }}-1}z_{\alpha } \right] . \end{aligned}$$

We deduce the last point of Lemma 3 easily. $\square$

Appendix B: Extinction Time

This subsection is devoted to the proof of Theorem 2 following ideas similar to the ones of the proof of Theorem 3 and Proposition 4.1 in Coron et al. (2018). Hence, we do not give all details, but explain only parts that are different.

Assume that $m_A\le m_0$, $m_a\le m_0$ and that $\mathbf{{Z}}^K(0)$ converges in probability to a deterministic vector $\mathbf{{z}^0}$ belonging to ${\mathcal {D}}^{A,a}_{m_A,m_a}$, Lemma 3 and Theorem 1 ensure that $(\mathbf{{Z}}^K(t),t\ge 0)$ reaches a neighborhood of the equilibrium $(\zeta _A,0,0,\zeta _a)$ after a finite time independent from K. Indeed, the process dynamics is close to the one of the limiting deterministic system (4).

To prove Theorem 2, it remains to estimate the time before all a-individuals in patch 1 and all A-individuals in patch 2 disappear. We denote it by

$$\begin{aligned} T^K_0=\inf \{t\ge 0, Z^K_{a,1}(t)+Z^K_{A,2}(t)=0\}, \end{aligned}$$

(26)

and we assume that the process is initially close to equilibrium $(\zeta _A,0,0,\zeta _a)$. The estimation is deduced from the following Lemma.

Lemma 4

There exist two positive constants $\varepsilon _0$ and $C_0$ such that for any $\varepsilon \le \varepsilon _0$, if there exists $\eta \in ]0,1/2[$ that satisfies $\max (|z_{A,1}^0-\zeta _A|,|z_{a,2}^0-\zeta _a|) \le \varepsilon$ and $\eta \varepsilon /2 \le z_{a,1}^0,z_{A,2}^0 \le \varepsilon /2$, then

$$\begin{aligned} \begin{aligned}&\text {for all } C>(\omega (A,a))^{-1}+C_0\varepsilon ,&\quad \mathbb {P}(T_0^K\le C \log (K)) \underset{K\rightarrow +\infty }{\rightarrow } 1,\\&\text {for all } 0\le C <(\omega (A,a))^{-1}-C_0\varepsilon ,&\quad \mathbb {P}(T_0^K\le C \log (K)) \underset{K\rightarrow +\infty }{\rightarrow } 0. \end{aligned} \end{aligned}$$

Proof

Following the first step of Proposition 4.1’s proof given by Coron et al. (2018), we prove that as long as the population processes $Z_{a,1}^K(t)$ and $Z_{A,2}^K(t)$ have small values, the processes $Z_{A,1}^K(t)$ and $Z_{a,2}^K(t)$ stay close to $\zeta _A$ and $\zeta _a$ respectively.

Then, by bounding death rates, birth rates and migration rates of $(Z^K_{a,1}(t),t\ge 0)$ and $(Z^K_{A,2}(t),t\ge 0)$, we are able to compare the dynamics of these two processes with the ones of

$$\begin{aligned} \left( \frac{{\mathcal {N}}_a(t)}{K},\frac{{\mathcal {N}}_A(t)}{K},\quad t\ge 0 \right) , \end{aligned}$$

where $({\mathcal {N}}_a(t),{\mathcal {N}}_A(t)) \in \mathbb {N}^{\{a,A\}}$ is a two types of branching process with types a and A and for which

• any $\alpha$-individual gives birth to a $\alpha$-individual at rate b,

• any $\alpha$-individual gives birth to a $\bar{\alpha }$-individual at rate $m_{\bar{\alpha }}$,

• any $\alpha$-individual dies at rate $b\beta _{\bar{\alpha }}+m_\alpha$.

The goal is thus to estimate the extinction time of such a subcritical two types of branching process. Let M(t) be the mean matrix of the multitype process, that is,

$$\begin{aligned} M(t)= \begin{pmatrix} \mathbb {E}\Big [\mathbb {E}\Big [{\mathcal {N}}_a(t)\Big |({\mathcal {N}}_a(0),{\mathcal {N}}_A(0))=(1,0)\Big ]\Big ] &{} &{} \mathbb {E}\Big [\mathbb {E}\Big [{\mathcal {N}}_A(t)\Big |({\mathcal {N}}_a(0),{\mathcal {N}}_A(0))=(1,0)\Big ]\Big ]\\ &{} &{} \\ \mathbb {E}\Big [\mathbb {E}\Big [{\mathcal {N}}_a(t)\Big |({\mathcal {N}}_a(0),{\mathcal {N}}_A(0))=(0,1)\Big ]\Big ] &{} &{} \mathbb {E}\Big [\mathbb {E}\Big [{\mathcal {N}}_A(t)\Big |({\mathcal {N}}_a(0),{\mathcal {N}}_A(0))=(0,1)\Big ]\Big ] \end{pmatrix}, \end{aligned}$$

and let G be the infinitesimal generator of the semigroup $\{M(t),t\ge 0\}$. From the book of Athreya and Ney (1972) p.202, we deduce a formula of G which is

$$\begin{aligned} G=\begin{pmatrix} -b(\beta _A-1)-m_a &{}\quad m_A \\ m_a &{}\quad -\,b(\beta _a-1)-m_A \end{pmatrix}. \end{aligned}$$

Applying Theorem 3.1 of Heinzmann (2009), we find that

$$\begin{aligned}&\mathbb {P}\Big (({\mathcal {N}}_a(t),{\mathcal {N}}_A(t))=(0,0) \Big |({\mathcal {N}}_a(0),{\mathcal {N}}_A(0))=(z_{a,1}^0 K,z_{A,2}^0 K)\Big )\nonumber \\&\quad = (1-c_a e^{rt})^{z_{a,1}^0 K}(1-c_A e^{rt})^{z_{A,2}^0 K}, \end{aligned}$$

(27)

where $c_a, c_A$ are two positive constants and r is the largest eigenvalue of the matrix G. With a simple computation, we find that $r=-\omega (A,a)$. From (27), we deduce that the extinction time is of order $\omega (A,a)^{-1}\log K$ when K tends to $+\,\infty$ by arguing as in step 2 of Proposition 4.1’s proof of Coron et al. (2018). This concludes the proof of Lemma 4. $\square$

Finally, this gives all elements to induce Theorem 2.