“Speculative Influence Network” during financial bubbles: application to Chinese stock markets

Abstract

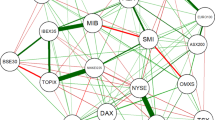
We introduce the Speculative Influence Network (SIN) to decipher the causal relationships between sectors (and/or firms) during financial bubbles. The SIN is constructed in two steps. First, we develop a Hidden Markov Model (HMM) of regime-switching between a normal market phase represented by a geometric Brownian motion and a bubble regime represented by the stochastic super-exponential Sornette and Andersen (Int J Mod Phys C 13(2):171–188, 2002) bubble model. The calibration of the HMM provides the probability at each time for a given security to be in the bubble regime. Conditional on two assets being qualified in the bubble regime, we then use the transfer entropy to quantify the influence of the returns of one asset i onto another asset j, from which we introduce the adjacency matrix of the SIN among securities. We apply our technology to the Chinese stock market during the period 2005–2008, during which a normal phase was followed by a spectacular bubble ending in a massive correction. We introduce the Net Speculative Influence Intensity variable as the difference between the transfer entropies from i to j and from j to i, which is used in a series of rank ordered regressions to predict the maximum loss (%MaxLoss) endured during the crash. The sectors that influenced other sectors the most are found to have the largest losses. There is some predictability obtained by using the transfer entropy involving industrial sectors to explain the %MaxLoss of financial institutions but not vice versa. We also show that the bubble state variable calibrated on the Chinese market data corresponds well to the regimes when the market exhibits a strong price acceleration followed by clear change of price regimes. Our results suggest that SIN may contribute significant skill to the development of general linkage-based systemic risks measures and early warning metrics.

Appendices

Appendix 1: “Bra-Ket” notations for probability formulas

This appendix introduces a convenient mathematical representation of probability distribution functions and of conditional density functions using notations involving bra-vector and ket-vector, according to the following definition:

• 1a. A single “bra-vector” $\langle \, A\,|$ indicates an element in “unconditional probability space” ${\mathscr {H}}$ as the image of mapping from a event A that belongs to the sample space $\Omega$. Similarly, $\langle \, A,B\,|$ denotes the “bra-vector” of event $A\cap B$. Compactly, $\langle \, A,B\,|$ also writes as $\langle \, AB\,|$.

• 1b. A single “ket-vector” $|B\,\rangle$ indicates an element in “condition space” ${\mathscr {M}}$ as the image of mapping from a event B that belongs to the sample space $\Omega$. Similarly, $|A,B\,\rangle$ denotes the “ket-vector” of event $A\cap B$.

• 2. The spaces ${\mathscr {H}}$ and ${\mathscr {M}}$ are both linear space satisfying the axioms such as the associativity and commutativity of addition, compatibility of scalar multiplication, distributivity of scalar multiplication, etc. For example, $k\cdot \langle \, A\,|+\langle \, B\,|\cdot k=k (\langle \, A\,|+\langle \, B\,|),\quad k \in \mathbb {R}$.

• 3. There is a binary operator “concatenation product”, denoted by “:”, between the vector in ${\mathscr {H}}$ and vector in ${\mathscr {M}}$. The output of $\langle \, A\,|:|B\,\rangle$ makes a complete pairwise bra-ket $\langle \,A\mid B \,\rangle$ as a number, which represents the conditional distribution $f(A\mid B)$. Generally, there is no associativity for scalar multiplication “$\cdot$” and “:”, i.e., $(k\cdot \langle \, A\,|):|B\,\rangle \ne k\,\langle \,A\mid B \,\rangle$. Where, $|\Omega \,\rangle$ is of exception so that $(k\cdot \langle \, A\,|):|\Omega \,\rangle = k\,\langle \,A\mid \Omega \,\rangle$.

• 4. For arbitrary unitary operator T which is defined on both ${\mathscr {H}}$ and ${\mathscr {M}}$, the notation $\langle \, A\,|T|B\,\rangle$ simultaneously means $\Bigl (\langle \, A\,| T\Bigr ):|B\,\rangle$ and $\langle \, A\,|:\Bigl (T|B\,\rangle \Bigr )$.

• 5a. The notation $|A\,\rangle \langle \, A\,|$ to concatenate a single “ket” vector and a single “bra” vector defines the operator to transform a “ket” (“bra”) into another “ket” (“bra”), which leads to

  • $\langle \, B\,|\,\Bigl (\,|A\,\rangle \langle \, A\,|\,\Bigr )=\langle \,B\mid A \,\rangle \cdot \langle \, A\,|=\langle \, B,A\,|$

  • $\Bigl (\,|A\,\rangle \langle \, A\,|\,\Bigr )\,|B\,\rangle =|A,B\,\rangle \cdot \langle \,A\mid B \,\rangle$

• 5b. Given $\Omega =\bigcup \nolimits _{i}C_i,\quad C_i\cap C_j=\phi$, then $I:=\sum \nolimits _i\,\,|C_i\,\rangle \langle \, C_i\,|$ gives the identical operator such that $\langle \, A\,|\, I = \langle \, A\,|$,   $I\, |B\,\rangle =|B\,\rangle$ and $\langle \, A\,|\,I\,|B\,\rangle =\langle \,A\mid B \,\rangle$.

In the strict sense, the unconditional distribution for event A should be a number $f(A)=\langle \,A\mid \Omega \,\rangle$. But as in all time one can first manipulate bra-vector in ${\mathscr {H}}$ and then try to concatenate the bra-vector result by $|\Omega \,\rangle$ in ${\mathscr {M}}$ to give the meaning of probability, in most cases without ambiguity, it is convenient to straightforward treat the bra-vector as the presentation of unconditional distribution, i.e., $f(A):=\langle \, A\,|$.

As for a random variable $\tilde{x}: \Omega \mapsto \mathbb {R}$, the above notations can also apply. One can use $\langle \, \tilde{x}=x\,|$ to represent a vectors in ${\mathscr {H}}$ that is same as $\langle \, \{\omega \mid \tilde{x}(\omega )=x\}\in {\mathscr {F}}\subset \Omega \,|$. The meaning of $|\tilde{x}=x\,\rangle$ is similar. Moreover, the notation $\langle \, \tilde{x}\,|$ (respectively, $|\tilde{x}\,\rangle$) indicates a set of “bra” (“ket”), i.e., $\langle \, \tilde{x}\,|=\bigl \{\langle \, \tilde{x}=x\,|: \forall x \in \mathbb {R}\bigr \}$ or a generic “bra-vector”(“ket-vector”) before $\tilde{x}$ finds a certain value x.

Further, according to the previous defined notations, the classic conditional probability and Bayesian formula can be rewritten as

• (Conditional probability formula): $\langle \,A\mid B \,\rangle =\dfrac{\langle \,AB\mid \Omega \,\rangle }{\langle \,B\mid \Omega \,\rangle }\quad$ or $\quad \langle \, AB\,|=\langle \,A\mid B \,\rangle \langle \, B\,|$

• (The Bayesian formula):    $\langle \,A\mid B \,\rangle =\langle \,A\mid \Omega \,\rangle \dfrac{\langle \,B\mid A \,\rangle }{\langle \,B\mid \Omega \,\rangle }\quad$ or    $\langle \,A\mid B \,\rangle \langle \, B\,|=\langle \,B\mid A \,\rangle \langle \, A\,|$

With the listed formal rules and the basic formula, we can easily give the derivations for the following famous formula in probability theory.

• 1. (The Law of Total probability): $\langle \, A\,|=\langle \, A\,|\,I=\langle \, A\,|\Bigl (\sum _i|B_i\,\rangle \langle \, B_i\,|\Bigr )=\sum _i\langle \,A\mid B_i \,\rangle \langle \, B_i\,|$

• 2. (Decomposed Conditional Joint Density):

  $$\begin{aligned} \langle \,A,B\mid C \,\rangle&=\langle \, AB\,|:|C\,\rangle =(\langle \,A\mid B \,\rangle \langle \, B\,|):|C\,\rangle \\&=\langle \, A\,|\,\Bigl (|B\,\rangle \langle \, B\,|\,\Bigr )\,|C\,\rangle =\langle \, A\,|:\Bigl (|B,C\,\rangle \langle \,B\mid C \,\rangle \Bigr )\\&=\langle \,A\mid B,C \,\rangle \langle \,B\mid C \,\rangle \end{aligned}$$

• 3. (Multivariate Bayesian Formula):

  $$\begin{aligned} \langle \,A\mid B,C \,\rangle&=\frac{\langle \,A\mid B,C \,\rangle \langle \,B\mid C \,\rangle }{\langle \,B\mid C \,\rangle }=\frac{\langle \, A\,|\,(\,|B\,\rangle \langle \, B\,|\,)\,|C\,\rangle }{\langle \,B\mid C \,\rangle }\\&=\frac{\langle \, AB\,|:|C\,\rangle }{\langle \,B\mid C \,\rangle }=\frac{\langle \, BA\,|:|C\,\rangle }{\langle \,B\mid C \,\rangle }=\frac{\langle \, B\,|\,(\,|A\,\rangle \langle \, A\,|\,)\,|C\,\rangle }{\langle \,B\mid C \,\rangle }\\&=\langle \,A\mid C \,\rangle \frac{\langle \,B\mid A,C \,\rangle }{\langle \,B\mid C \,\rangle } \end{aligned}$$

Appendix 2: Proof of Eq. (10)

Proof

Since $p_t^{-n}\mid p_{t-1}^{-n}\,\sim \,\mathcal {N}(p_{t-1}^{-n}-n\mu _1,n^2\sigma _1^2)$, one can get

$$\begin{aligned} \langle \,p_t^{-n}\mid p_{t-1}^{-n} \,\rangle =\dfrac{1}{\sqrt{2\pi }\sigma _1}\exp \left[ -\dfrac{1}{2}\cdot \left( \dfrac{p_t^{-n}-p_{t-1}^{-n}-\mu _1}{\sigma _1}\right) ^2\right] . \end{aligned}$$

(38)

With the density transformation formula $f_{\tilde{x}|\tilde{y}}(x|y)=f_{\tilde{x}|\tilde{y}}(\phi (x)|y)|\phi '(x)|$, or equivalently $\langle \,x\mid y \,\rangle =\langle \,\phi (x)\mid y \,\rangle \cdot |\phi '(x)|$, Eq. (38) further leads to

$$\begin{aligned} \langle \,p_t\mid p_{t-1} \,\rangle =\dfrac{1}{\sqrt{2\pi }\cdot n\sigma _1}\exp \left[ -\dfrac{1}{2}\cdot \left( \dfrac{p_t^{-n}-p_{t-1}^{-n}+n\mu _1}{n\sigma _1}\right) ^2\right] \cdot n p_t^{-(n+1)} \end{aligned}$$

(39)

From the definition $y_t=\ln p_t$, and using the density transformation formula again, we obtain

$$\begin{aligned} \langle \,y_t\mid y_{t-1} \,\rangle= & {} \langle \,e^{y_t}\mid y_{t-1} \,\rangle e^{y_t}=\langle \,p_t\mid y_t \,\rangle p_t\end{aligned}$$

(40)

$$\begin{aligned}= & {} \dfrac{1}{\sqrt{2\pi }\cdot n\sigma _1}\exp \left[ -\dfrac{1}{2}\cdot \left( \dfrac{e^{-ny_t}-e^{-ny_{t-1}}+n\mu _1}{n\sigma _1}\right) ^2\right] \cdot n e^{-ny_t}\nonumber \\ \end{aligned}$$

(41)

Consequently, we have

$$\begin{aligned} \ln \langle \,y_t\mid 1,1,y_{t-1} \,\rangle =-\dfrac{1}{2}\ln 2\pi -\ln n\sigma _1-\dfrac{1}{2}\cdot \left( \dfrac{e^{-ny_t}-e^{-ny_{t-1}}+n\mu _1}{n\sigma _1}\right) ^2+\ln n -n y_t \end{aligned}$$

(42)

$\square$

Appendix 3: Derivations for the equations in EM algorithm

1.1 Proof of the Eq. (14) from Eq. (13)

Proof

$$\begin{aligned} \mathcal {\ln L}_{\pmb {\theta }\,\mid \,\pmb {\theta }^{(k-1)}}&=\sum _{1\ldots T}\ln \langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }}\,\,\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\nonumber \\&=\sum _{1\ldots T}\ln (\,\langle \,y^{T}_{\multimap }\mid s^{T}_{\multimap } \,\rangle _{\pmb {\theta }}\langle \, s^{T}_{\multimap }\,|_{\pmb {\theta }}\,)\,\,\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\nonumber \\&=\sum _{1\ldots T}\ln \langle \,y^{T}_{\multimap }\mid s^{T}_{\multimap } \,\rangle _{\pmb {\theta }}\,\,\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}+\sum _{1\ldots T}\ln \langle \, s^{T}_{\multimap }\,|_{\pmb {\theta }}\,\,\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}} \end{aligned}$$

(43)

For the first item in the r.h.s. of (43), we can further obtain

$$\begin{aligned}&\sum _{1\ldots T}\ln \langle \,y^{T}_{\multimap }\mid s^{T}_{\multimap } \,\rangle _{\pmb {\theta }}\,\,\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\\&=\sum _{1\ldots T}\left( \sum _{t=1}^T\ln \langle \,y_{t}\mid s_t,s_{t-1},y^{t-1}_{\multimap } \,\rangle _{\pmb {\theta }}\right) \,\,\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\\&=\sum _{t=1}^T\left( \sum _{t,t-1}\sum _{/t,/t-1}\ln \langle \,y_{t}\mid s_t,s_{t-1},y^{t-1}_{\multimap } \,\rangle _{\pmb {\theta }}\,\,\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\right) \\&=\sum _{t=1}^T\sum _{t,t-1}\left( \ln \langle \,y_{t}\mid s_t,s_{t-1},y^{t-1}_{\multimap } \,\rangle _{\pmb {\theta }}\,\sum _{/t,/t-1}\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\right) \\&=\sum _{t=1}^T\left( \sum _{t,t-1}\ln \langle \,y_{t}\mid s_t,s_{t-1},y^{t-1}_{\multimap } \,\rangle _{\pmb {\theta }}\,\langle \, y^{T}_{\multimap },s_{t},s_{t-1}\,|_{\pmb {\theta }^{(k-1)}}\right) \\&=\langle \, y^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}} \sum _{t=1}^T\left( \sum _{t,t-1}\ln \langle \,y_{t}\mid s_t,s_{t-1},y^{t-1}_{\multimap } \,\rangle _{\pmb {\theta }}\,\langle \,s_{t-1},s_t\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) \end{aligned}$$

where the notation $\sum \nolimits _{/t,/t-1}$ represents the summation for all states $s_{\tau }, \tau =1,\ldots ,T$, except for $s_{t-1}$ and $s_t$. The second term in the r.h.s. of (43) leads to

$$\begin{aligned}&\sum _{1\ldots T}\ln \langle \, s^{T}_{\multimap }\,|_{\pmb {\theta }}\,\,\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\\&=\sum _{1\ldots T}\left( \sum _{t=1}^T\ln \langle \,s_t\mid s_{t-1} \,\rangle _{\pmb {\theta }}\right) \,\,\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\\&=\sum _{t=1}^T\left( \sum _{t,t-1}\sum _{/t,/t-1}\ln \langle \,s_t\mid s_{t-1} \,\rangle _{\pmb {\theta }}\,\,\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\right) \\&=\sum _{t=1}^T\sum _{t,t-1}\left( \ln \langle \,s_t\mid s_{t-1} \,\rangle _{\pmb {\theta }}\sum _{/t,/t-1}\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\right) \\&=\langle \, y^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\sum _{t=1}^T\left( \sum _{t,t-1}\ln \langle \,s_t\mid s_{t-1} \,\rangle _{\pmb {\theta }}\,\langle \,s_{t-1},s_t\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) \end{aligned}$$

Thus, we finally obtain (14)

$$\begin{aligned}&\mathcal {\ln L}_{\pmb {\pmb {\theta }}^{(k)}\,\mid \,\pmb {\theta }^{(k-1)}}= \langle \, y^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}\\&\cdot \left( \sum _{t=1}^T \sum _{\begin{array}{c} \;\;s_t=1,0\\ s_{t-1}=1,0 \end{array}}\Bigl (\ln \langle \,y_{t}\mid s_t,s_{t-1},y_{t-1} \,\rangle _{\pmb {\theta }^{(k)}}+\ln \langle \,s_t\mid s_{t-1} \,\rangle _{\pmb {\theta }^{(k)}}\,\Bigr )\langle \,s_{t-1},s_t\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) \end{aligned}$$

$\square$

1.2 Derivation of the formulas to determine the first four parameters of the HMM

Since $\langle \, s^{T}_{\multimap }\,|_{\pmb {\theta }}$ does not depend on $\pmb {\theta }=(\mu _0,\sigma _0, \mu _1, \sigma _1, n)$, one can ignore the second term in Eq. (43) when calibrating the parameters of the HMM.

In order to compute $\mu _0^{(k)}$, the first-order condition of the first term in Eq. (43) reads

$$\begin{aligned} \sum _{t=1}^T \left( \sum _{\begin{array}{c} s_t=1,0\\ s_{t-1}=1,0 \end{array}}\dfrac{\partial }{\partial \mu _0}\ln \langle \,y_{t}\mid s_t,s_{t-1},y_{t-1} \,\rangle _{\pmb {\theta }}\,\langle \,s_t,s_{t-1}\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) =0 \end{aligned}$$

(44)

which leads to

$$\begin{aligned}&\sum _{t=1}^T \left( \dfrac{y_t-y_{t-1}-\mu _0}{\sigma _0}\,\langle \,s_t=0,s_{t-1}=0\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) =0\\&\Longrightarrow \qquad \mu _0=\dfrac{\sum _{t=1}^T (y_t-y_{t-1})\langle \,s_t=0,s_{t-1}=0\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}}{\sum _{t=1}^T \langle \,s_t=0,s_{t-1}=0\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}}\\&\Longrightarrow \qquad \mu _0^{(k)}=\dfrac{\sum _{t=1}^T \omega _{(0,0);t}^{(k-1)}(y_t-y_{t-1})}{\sum _{t=1}^T\omega _{(0,0);t}^{(k-1)}} \end{aligned}$$

In order to compute $\sigma _0^{(k)}$, the first-order condition of the first term in Eq. (43) reads

$$\begin{aligned} \sum _{t=1}^T \left( \sum _{\begin{array}{c} s_t=1,0\\ s_{t-1}=1,0 \end{array}}\dfrac{\partial }{\partial \sigma _0}\ln \langle \,y_{t}\mid s_t,s_{t-1},y_{t-1} \,\rangle _{\pmb {\theta }}\,\langle \,s_t,s_{t-1}\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) =0 \end{aligned}$$

(45)

which leads to

$$\begin{aligned} \sum _{t=1}^T \left( -\dfrac{1}{\sigma _0}+\dfrac{(y_t-y_{t-1}-\mu _0)^2}{\sigma _0^3}\,\right) \langle \,s_t=0,s_{t-1}=0\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}=0\\ \Longrightarrow \qquad \sigma _0^{(k)}=\sqrt{\dfrac{\sum _{t=1}^T \omega _{(0,0);t}^{(k-1)}(y_t-y_{t-1}-\mu _0^{(k)})^2}{\sum _{t=1}^T\omega _{(0,0);t}^{(k-1)}}}&\end{aligned}$$

In order to compute $\mu _1^{(k)}$, the first-order condition of the first term in Eq. (43) reads

$$\begin{aligned} \sum _{t=1}^T \left( \sum _{\begin{array}{c} s_t=1,0\\ s_{t-1}=1,0 \end{array}}\dfrac{\partial }{\partial \mu _1}\ln \langle \,y_{t}\mid s_t,s_{t-1},y_{t-1} \,\rangle _{\pmb {\theta }}\,\langle \,s_t,s_{t-1}\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) =0 \end{aligned}$$

(46)

which leads to

$$\begin{aligned}&\sum _{t=1}^T \left( -\dfrac{p_t^{-n}-p_{t-1}^{-n}+n \mu _1}{n\sigma _1^2}\,\right) \langle \,s_t=1,s_{t-1}=1\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}=0\\&\Longrightarrow \qquad \sum _{t=1}^T \left( -p_t^{-n}+p_{t-1}^{-n}-n \mu _1\,\right) \omega _{(1,1);t}^{(k-1)}=0\\&\Longrightarrow \qquad \mu _1^{(k)}=\dfrac{\sum _{t=1}^T \omega _{(1,1);t}^{(k-1)}(p_{t-1}^{-n}-p_t^{-n})}{n \sum _{t=1}^T\omega _{(1,1);t}^{(k-1)}} \end{aligned}$$

In order to compute $\sigma _1^{(k)}$, the first-order condition of the first term in Eq. (43) reads

$$\begin{aligned} \sum _{t=1}^T \left( \sum _{\begin{array}{c} s_t=1,0\\ s_{t-1}=1,0 \end{array}}\dfrac{\partial }{\partial \sigma _1}\ln \langle \,y_{t}\mid s_t,s_{t-1},y_{t-1} \,\rangle _{\pmb {\theta }}\,\langle \,s_t,s_{t-1}\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) =0 \end{aligned}$$

(47)

which leads to

$$\begin{aligned}&\sum _{t=1}^T \left( \dfrac{1}{\sigma _1}-\dfrac{(p_t^{-n}-p_{t-1}^{-n}+n \mu _1)^2}{n^2\sigma _1^3}\,\right) \langle \,s_t=1,s_{t-1}=1\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}=0\\&\Longrightarrow \qquad \sum _{t=1}^T \left[ (p_t^{-n}-p_{t-1}^{-n}+n \mu _1)^2-n^2\sigma _1^2\,\right] \omega _{(1,1);t}^{(k-1)}=0\\&\Longrightarrow \qquad \sigma _1^{(k)}=\sqrt{\dfrac{\sum _{t=1}^T \omega _{(1,1);t}^{(k-1)}(p_{t}^{-n}-p_{t-1}^{-n}+n\mu _1^{(k)})^2}{n^2 \sum _{t=1}^T\omega _{(1,1);t}^{(k-1)}}} \end{aligned}$$

1.3 Derivation for Eq. (15) to solve for n

To compute $n^{(k)}$, one should solve the first-order condition of the first term in Eq. (43) with respect to n, that is

$$\begin{aligned} \sum _{t=1}^T \left( \sum _{\begin{array}{c} s_t=1,0\\ s_{t-1}=1,0 \end{array}}\dfrac{\partial }{\partial n}\ln \langle \,y_{t}\mid s_t,s_{t-1},y_{t-1} \,\rangle _{\pmb {\theta }}\,\langle \,s_t,s_{t-1}\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) =0 \end{aligned}$$

(48)

which gives,

$$\begin{aligned}&\sum _{t=1}^T \Biggl ( -\dfrac{(p_t^{-n}-p_{t-1}^{-n}+n\mu _1)(-p_t^{-n}\ln p_t+p_{t-1}^{-n}\ln p_{t-1}+\mu _1)}{n^2\sigma _1^2}\nonumber \\&\quad +\dfrac{(p_t^{-n}-p_{t-1}^{-n}+n\mu _1)^2}{n^3\sigma _1^2}-\frac{1}{n}+\frac{1}{n}-\ln p_t\Biggr )\,\,\omega _{(1,1):t}^{(k-1)}=0 \end{aligned}$$

(49)

Note that $\displaystyle \sum \nolimits _{t=1}^T \left( \dfrac{(p_t^{-n}-p_{t-1}^{-n}+n\mu _1)^2}{n^3\sigma _1^2}-\frac{1}{n}\right) \,\omega _{(1,1):t}^{(k-1)}=0$. Thus, the above equation can be reduced to

$$\begin{aligned}&\sum _{t=1}^T \left( -\dfrac{(p_t^{-n}-p_{t-1}^{-n}+n\mu _1)(-p_t^{-n}\ln p_t+p_{t-1}^{-n}\ln p_{t-1}+\mu _1)}{n^2\sigma _1^2}+\frac{1}{n}-\ln p_t\right) \nonumber \\&\quad \,\times \omega _{(1,1):t}^{(k-1)}=0 \end{aligned}$$

(50)

1.4 Derivation of the formulas to compute the optimal posterior transition probability from $s_{t-1}$ to $s_t$

Since $\langle \,s_t\mid s_{t-1} \,\rangle _{\pmb {\theta }^{(k)}}$ is only related to the second term in Eq. (43), we can ignore the first term when performing the optimization:

$$\begin{aligned} \sum _{1\ldots T}\ln \langle \, s^{T}_{\multimap }\,|_{\pmb {\theta }}\,\,\langle \, y^{T}_{\multimap },s^{T}_{\multimap }\,|_{\pmb {\theta }^{(k-1)}}&= \sum _{t=1}^T\left( \sum _{t,t-1}\ln \langle \,s_t\mid s_{t-1} \,\rangle _{\pmb {\theta }}\,\langle \,s_{t},s_{t-1}\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) \\&=\sum _{t=1}^T\left( \sum _{j,i}\ln q_{ij}^{(k)}\,\langle \,j,i\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) \end{aligned}$$

Without loss of generality, the first-order condition against $q_{i1}$ leads to

$$\begin{aligned} 0&=\sum _{t=1}^T\left( \dfrac{\partial }{\partial q_{i1}^{(k)} }\ln q_{ij}^{(k)}\,\langle \,i,j\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) \\&=\sum _{t=1}^T\left( \dfrac{1}{q_{i1}^{(k)}}\langle \,1,i\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}-\dfrac{1}{1-q_{i1}^{(k)}}\langle \,0,i\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}\right) \end{aligned}$$

Then we have

$$\begin{aligned}&q_{i1}^{(k)}=\dfrac{\sum _{t=1}^T\langle \,1,i\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}}{\sum _{t=1}^T(\langle \,1,i\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}+\langle \,0,i\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}})}=\dfrac{\sum _{t=1}^T\langle \,1,i\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}}{\sum _{t=1}^T\langle \,i\mid y^{T}_{\multimap } \,\rangle _{\pmb {\theta }^{(k-1)}}} \end{aligned}$$

It is the optimal posterior transition probability after the kth iteration, $q_{ij}^{(k)}$, when $j=1$.

1.5 Reasoning to replace $\langle \,s_t\mid s_{t+1},y^{t}_{\multimap },y^{\multimap }_{t+1} \,\rangle$ by $\langle \,s_t\mid s_{t+1},y^{t}_{\multimap } \,\rangle$ in Eq. (20)

$$\begin{aligned} \langle \,s_t\mid s_{t+1},y^{t}_{\multimap },y^{\multimap }_{t+1} \,\rangle= & {} \frac{\langle \, s_t\,|:\biggl (\,|s_{t+1},y^{t}_{\multimap },y^{\multimap }_{t+1}\,\rangle \,\biggr )\,\langle \,y^{\multimap }_{t+1}\mid s_{t+1},y^{t}_{\multimap } \,\rangle }{\langle \,y^{\multimap }_{t+1}\mid s_{t+1},y^{t}_{\multimap } \,\rangle } \end{aligned}$$

(51)

$$\begin{aligned}= & {} \frac{\langle \, s_t\,|:\biggl (\,|s_{t+1},y^{t}_{\multimap },y^{\multimap }_{t+1}\,\rangle \,\langle \,y^{\multimap }_{t+1}\mid s_{t+1},y^{t}_{\multimap } \,\rangle \,\biggr )}{\langle \,y^{\multimap }_{t+1}\mid s_{t+1},y^{t}_{\multimap } \,\rangle } \end{aligned}$$

(52)

$$\begin{aligned}= & {} \frac{\langle \, s_t\,|\,\biggl (\,|y^{\multimap }_{t+1}\,\rangle \langle \, y^{\multimap }_{t+1}\,|\,\biggr )\,|s_{t+1},y^{t}_{\multimap }\,\rangle }{\langle \,y^{\multimap }_{t+1}\mid s_{t+1},y^{t}_{\multimap } \,\rangle } \end{aligned}$$

(53)

$$\begin{aligned}= & {} \frac{\biggl (\,\langle \,s_t\mid y^{\multimap }_{t+1} \,\rangle \langle \, y^{\multimap }_{t+1}\,|\,\biggr ):|s_{t+1},y^{t}_{\multimap }\,\rangle }{\langle \,y^{\multimap }_{t+1}\mid s_{t+1},y^{t}_{\multimap } \,\rangle }\nonumber \\= & {} \frac{\langle \, y^{\multimap }_{t+1}\,|\,\biggl (\,|s_t\,\rangle \langle \, s_t\,|\,\biggr )\,|s_{t+1},y^{t}_{\multimap }\,\rangle }{\langle \,y^{\multimap }_{t+1}\mid s_{t+1},y^{t}_{\multimap } \,\rangle } \end{aligned}$$

(54)

$$\begin{aligned}= & {} \frac{\langle \,y^{\multimap }_{t+1}\mid s_t,s_{t+1},y^{t}_{\multimap } \,\rangle \langle \,s_t\mid s_{t+1},y^{t}_{\multimap } \,\rangle }{\langle \,y^{\multimap }_{t+1}\mid s_{t+1},y^{t}_{\multimap } \,\rangle }\qquad \end{aligned}$$

(55)

By assuming that the joint distribution of $( y_{t+1},y_{t+2},\ldots ,y_{T} )$ is irrelevent to $s_t$, we can eliminate the denominator and easily recover (55) for $\langle \,s_t\mid s_{t+1},y^{t}_{\multimap } \,\rangle$