The Capacity Performance of OFDM Systems with Nonlinear Pulse Blanking in Frequency Selective Fading Channels

Abstract

Nonlinear pulse blanking is a widely applied method to mitigate the impulse interference of orthogonal frequency division multiplexing (OFDM) systems. To quantitatively analyze the capacity of the OFDM system with nonlinear pulse blanking, the analytical expressions of the instantaneous output signal-to-interference-plus-noise ratio of the OFDM system with ideal blanking, peak value blanking, and optimum threshold blanking are first derived. The probability density function of the instantaneous capacity of the OFDM system with nonlinear pulse blanking is then estimated by the finite mixture with the expectation–maximization algorithm. The ergodic capacity and the probability of the outage capacity of the OFDM system with nonlinear pulse blanking are obtained based on the estimated probability density function. Finally, the simulation results are provided to indicate its good agreement with the theoretical results.

1 Introduction

The orthogonal frequency division multiplexing (OFDM) scheme has several advantages such as its high spectral efficiency, robustness to channel fading, and easy implementation as compared with the single carrier transmission scheme. Hence, the OFDM transmission scheme has been widely adopted in many modern communication systems [1]. The received signal of an OFDM system in practical applications is not only affected by additive Gaussian white noise (AWGN) but also by impulsive noise generated by vehicle ignition devices, adjacent channel electromagnetic radiation, and electrical devices of power lines [2,3,4,5]. Since the statistical properties of impulse noise are quite different than that of AWGN, the transmission reliability of an OFDM system, which is designed and optimized under the assumption of AWGN, severely decreases due to impulse noise interference. Hence, it is of great significance to conduct research on the impulse interference mitigation of OFDM systems.

To improve the transmission reliability of an OFDM system with impulse interferences, a great deal of research has been conducted on the mitigation of impulse noise. These research studies can be classified into three categories: nonlinear impulse interference suppression such as pulse blanking, pulse clipping, and joint pulse blanking and pulse clipping [6,7,8,9,10]; interference mitigation based on impulse signal reconstruction such as decision-directed and compressed sensing [11,12,13,14,15,16]; and impulse mitigation based on coding and iterative decoding [17, 18]. Although the transmission reliability of an OFDM system with the nonlinear impulse interference suppression method is inferior to the other two methods, the nonlinear impulse interference suppression method has many advantages such as its low computational complexity, easy engineering implementation, and strong adaptability [19]. Therefore, the nonlinear impulse interference suppression method is widely used in OFDM systems.

In the field of the nonlinear impulse interference suppression for OFDM systems, the related research is given as follows. Haffenden [6] and Cowley [7] first proposed an impulse mitigation method based on pulse blanking and pulse clipping. To apply this method to an OFDM receiver, two key issues should be addressed: (1) the optimal threshold of pulse blanking and pulse clipping and (2) the elimination of inter-carrier interference (ICI) caused by nonlinear pulse blanking. To address the optimal threshold setting problem of pulse blanking, Zhidkov [20] proposed a method based on maximizing the output SNR criterion in AWGN channels. Epple [21] further proposed an adaptive threshold optimization method based on maximizing the SINR criterion. Recently, a threshold setting method based on the peak value amplitude of received OFDM signals was presented by Alsusa [22, 23]. To mitigate the ICI caused by pulse blanking, Yih [24] proposed an iterative ICI cancellation scheme, while Epple [25] presented a signal combination method based on the maximization of the SINR criterion. Furthermore, Darsena et al. [26] proposed a frequency-domain linear FIR equalizer.

In the performance analysis of an OFDM system with impulse interference, Ghosh [27] first compared the influence of impulse noise on the transmission reliability of a single carrier and a multi-carrier system. Ma [28] derived the bit error rate performance of an OFDM system over a multipath and impulse noise environment. Amirshahi [29] further extended this result to the coded OFDM system. Liu [30] investigated the symbol error probability of an OFDM system with ideal pulse blanking over the frequency-selective fading channel, and this result was further extended to an OFDM system with peak value blanking in [31]. In addition, Zhang et al. [32] investigated the symbol error ratio performance of an OFDM system in the hidden semi-Markov impulse channel. Although many studies on nonlinear impulse interference have been presented, the effect of nonlinear impulse interference suppression on the capacity performance of an OFDM system has not been fully understood. These are the primary objectives of our study: (1) to generate the analytical expressions of the capacity of an OFDM system with nonlinear pulse blanking and (2) to compare the performance of an OFDM system with different pulse blanking schemes from the perspective of the channel capacity.

In this paper, the probability density function (PDF) of the instantaneous channel capacity of an OFDM system is derived by the finite mixture with expectation–maximization (FM-EM) algorithm over the frequency-selective Rayleigh and Rician fading channels. The ergodic and the probability of the outage capacity of an OFDM system with nonlinear pulse blanking are obtained based on the PDF of the instantaneous channel capacity of an OFDM system. At the end, theoretical results are validated by the computer simulation results.

The contributions of this paper include the following two aspects: (1) the ergodic capacity and the probability of the outage capacity of an OFDM system with pulse blanking are derived based on the FM-EM algorithm and (2) from the perspective of the channel capacity, three nonlinear blanking schemes are compared, specifically ideal pulse blanking, peak value blanking, and optimum threshold blanking.

The rest of this paper is organized as follows. In Sect. 2, the model of OFDM system with nonlinear pulse blanking is introduced. In Sect. 3, the instantaneous SINR expressions of an OFDM system with nonlinear pulse blanking are derived. In addition, the ergodic capacity and the probability of the outage capacity of a nonlinear OFDM system are presented in Sect. 4. The computer simulation results and analysis are presented in Sect. 5. Finally, Sect. 6 presents the conclusions.

2 System Model

Fig. 1

Model of the OFDM system with nonlinear pulse blanking

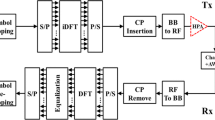
The model of the OFDM system with nonlinear pulse blanking is illustrated in Fig. 1. In the OFDM transmitter, the information bit vector ${\mathbf {I}}$ is first mapped into ${\mathbf {X}}=\left[ X_{0},\ldots ,X_{k},\ldots ,X_{N-1}\right] ^T$, where N is the number of the modulated symbols. The k-th symbol $X_k$ of ${\mathbf {X}}$ is assumed to be independent and identically distributed (i.i.d.) with $E\left[ {X_k } \right] = 0$ and $E\left[ {\left| {X_k } \right| ^2 } \right] = \sigma _s^2$. The modulated symbol vector ${\mathbf {X}}$ is then transformed into ${\mathbf {x}}$ by the N-points inverse discrete Fourier transform (IDFT) operation, of which the output signal vector of the IDFT is presented as follows:

$$\begin{aligned} {\mathbf{x}} = \mathbf{F}^{ - 1} \cdot {\mathbf{X}} \end{aligned}$$

(1)

where $\mathbf{F}^{ - 1}$ denotes the IDFT matrix, which is expressed as follows:

$$\begin{aligned} \mathbf{F}_{n,k}^{ - 1} = \frac{1}{{\sqrt{N} }}e^{2\pi j\frac{{kn}}{N}} ,\quad n,k = 0, \ldots ,N - 1 \end{aligned}$$

(2)

where k represents the subcarrier index in the frequency domain and n denotes the samples index in the time domain. As the IDFT operation is a unitary transformation, the statistical property of ${\mathbf {x}}$ agrees with ${\mathbf {X}}$. Thus, $x_n$ is also i.i.d such that $E\left[ {x_n } \right] = 0$ and $E\left[ {\left| {x_n } \right| ^2 } \right] = \sigma _s^2$. Finally, the transmitted signal ${\mathbf {x}}$ is inserted the cycle prefix (CP) and sent to a multipath fading channel.

In the receiver, assuming that the symbol timing synchronization has been established by the OFDM receiver, after the removal of the CP, the output signal vector ${\mathbf{r}} = [r_0 ,r_1 , \ldots ,r_n , \ldots ,r_{N - 1} ]^T$ can be expressed as follows:

$$\begin{aligned} {\mathbf {r}} = {\mathbf {x}} \otimes {\mathbf {h}} + {\mathbf {n}} + {\mathbf {i}} \end{aligned}$$

(3)

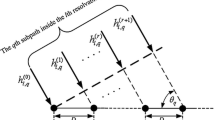
where $\otimes$ denotes the discrete circular convolution operator. ${\mathbf {h}} = \left[ {h_0 ,h_1 , \ldots h_l , \ldots ,h_{L - 1} } \right]$ denotes the discrete-time channel impulse response with L paths and the discrete-time channel power is normalized to one, i.e., $\sum \nolimits _{l = 0}^{L - 1} {E\left[ {\left| {h_l } \right| ^2 } \right] = 1}$, where $h_l$ is an i.i.d. complex Gaussian random variable. ${{\mathbf {n}}} = \left[ {n_0 , \ldots ,n_n , \ldots ,n_{N - 1} } \right] ^T$ denotes the complex AWGN vector, where $n_n$ is an i.i.d complex Gaussian random variable with a mean of zero and a variance $\sigma _n^2$. ${\mathbf {i}} = \left[ {i_0 ,i_1 , \ldots ,i_n , \ldots ,i_{N - 1} } \right] ^T$ represents the impulse noise vector coming from the channel, where $i_n$ is modeled as a Bernoulli–Gaussian random variable [27, 28], which can be expressed as:

$$\begin{aligned} i_n = b_n \cdot g_n , \quad n = 0, \ldots ,N - 1 \end{aligned}$$

(4)

where $g_n$ is an i.i.d. complex white Gaussian noise with a mean of zero and a variance $\sigma _g^2$, and $b_n$ is the Bernoulli sequence 1 and 0 with probabilities p and $1-p$, respectively. The input signal-to-noise ratio is defined as SNR $\buildrel {\Delta } \over = {{\sigma _s^2 } \big / {\sigma _n^2 }}$, and the input signal-to-interference ratio is defined as SIR $\buildrel {\Delta } \over = {{\sigma _s^2 } \big / {\sigma _g^2 }}$.

To mitigate the adverse effect of the impulse noise on the OFDM receiver, a nonlinear pulse blanking scheme is adopted to eliminate the impulse interference. The output signal vector of the nonlinear pulse blanking unit can be expressed as follows:

$$\begin{aligned} {\mathbf {y}} = {{\mathbf {D}}} \cdot {\mathbf {r}} \end{aligned}$$

(5)

where ${{\mathbf {D}}} = {\textit{diag}}\left( {d_0 , \ldots d_n , \ldots ,d_{N - 1} } \right)$ denotes a nonlinear pulse blanking matrix such that ${\textit{diag}}\left( \cdot \right)$ represents a diagonal matrix with $N \times N$. The signal vector ${\mathbf {y}}$ is then transformed into frequency domain vector ${\mathbf{Y}} = \left[ {Y_0 , \ldots ,Y_k , \ldots ,Y_{N - 1} } \right] ^T$ by the N-points discrete Fourier transform (DFT) operation. Thus, the output signal vector of the DFT is given by:

$$\begin{aligned} {{\mathbf {Y}}} = {{\mathbf {F}}} \cdot {{\mathbf {y}}} \end{aligned}$$

(6)

where ${\mathbf {F}}$ denotes the DFT matrix, which is expressed as follows:

$$\begin{aligned} {{\mathbf {F}}}_{k,n} = \frac{1}{{\sqrt{N} }}e^{ - 2\pi j\frac{{kn}}{N}} ,\quad k,n = 0, \ldots ,N - 1 \end{aligned}$$

(7)

The frequency response of the discrete time channel impulse response is given by ${\mathbf {H}} = \left[ {H_0, \ldots ,H_{N - 1} } \right] ^T$, such that:

$$\begin{aligned} {{\mathbf {H}}} = {{\mathbf {F}}} \cdot {{\mathbf {h}}} \end{aligned}$$

(8)

Assuming the channel frequency response is perfectly obtained by the channel estimator, the output signal ${\hat{Y}}_k$ of the equalizer during the k-th sub-channel is given by:

$$\begin{aligned} {\hat{Y}}_k = \frac{{H_k^* }}{{\left| {H_k } \right| ^2 }} \cdot Y_k , \quad k = 0,1, \ldots ,N - 1 \end{aligned}$$

(9)

where $H_k$ is the k-th component of ${\mathbf {H}}$ and $( \cdot )^*$ denotes the complex conjugate operator. Finally, the output signal vector ${\hat{{\mathbf {Y}}}} = [{\hat{Y}}_0 , \ldots ,{\hat{Y}}_k , \ldots ,{\hat{Y}}_{N - 1} ]^T$ of the equalizer is sent to the demodulator, wherein the output of the demodulator ${\hat{{\mathbf {I}}}}$ is the estimation of the transmitted information bit vector ${\mathbf {I}}$.

3 SINR of the OFDM Receiver

In this section, the output SINR expression of a conventional OFDM receiver is first presented in Sect. 3.1. The output SINR expressions of the nonlinear OFDM receivers with ideal blanking, peak value blanking, and optimum threshold blanking are then derived in Sects. 3.2, 3.3, and 3.4, respectively.

3.1 SINR of the Conventional OFDM Receiver

In Eq. (5), the presence of a nonlinear pulse blanking matrix ${\mathbf {D}}$ equal to a unit matrix with $N \times N$ reduces the OFDM receiver with nonlinear pulse blanking illustrated in Fig. 2 to a conventional OFDM receiver. Substituting Eq. (3) into Eq. (5), the output signal vector of the nonlinear pulse blanking unit can be rewritten as follows:

$$\begin{aligned} {\mathbf{y}} = {\mathbf{r}} \end{aligned}$$

(10)

The signal vector ${\mathbf {y}}$ is further transformed into the frequency domain by the N-points DFT operation, such that the output signal vector of the DFT can be expressed as follows:

$$\begin{aligned} {\mathbf{Y}} = {\mathbf{HX}} + \mathbf{N} + \mathbf{I} \end{aligned}$$

(11)

In Eq. (11), ${\mathbf{N}} = {\mathbf{F}} \cdot {\mathbf{n}}$ denotes a frequency domain noise vector, and ${\mathbf{I}} = {{\mathbf {F}}} \cdot {\mathbf{i}}$ denotes a frequency domain noise vector caused by the impulse noise in the time domain. The k-th component of ${\mathbf {Y}}$ is presented as follows:

$$\begin{aligned} Y_k = X_k \cdot H_k + N_k + I_k ,\quad k = 0,1,\ldots ,N - 1 \end{aligned}$$

(12)

where $N_k$ and $I_k$ are the k-th components of the vectors ${\mathbf {N}}$ and ${\mathbf {I}}$, respectively. Since ${\mathbf {F}}$ is a unitary matrix, the statistical property of ${\mathbf {N}}$ agrees with ${\mathbf {n}}$. Therefore, $N_k$ is also an i.i.d. complex Gaussian random variable with a mean of zero and a variance $\sigma _n^2$.

According to Eq. (12), $Y_k$ consists of two parts: the first term on the righthand side represents the desired signal in the k-th sub-channel, and the rest of the two terms represent the noise signal, which is contributed by the AWGN and the impulse noise. Therefore, Eq. (12) can be rewritten as follows:

$$\begin{aligned} Y_k = U_k + {\tilde{N}}_k ,\quad k = 0,1, \ldots , N - 1 \end{aligned}$$

(13)

where $U_k = X_k \cdot H_k$ denotes the desired signal during the k-th sub-channel, ${\tilde{N}}_k$ represents the equivalent frequency domain noise, which is defined as follows:

$$\begin{aligned} {\tilde{N}}_k = \left\{ \begin{array}{ll} N_k,&{}\quad b_n = 0 \\ N_k + G_k ,&{}\quad b_n = 1 \\ \end{array} \right. \end{aligned}$$

(14)

In Eq. (14), $G_k$ is the k-th component of ${\mathbf{G = }}{{\mathbf {F}}} \cdot {\mathbf{g}}$, such that $G_k\sim {{{{\mathcal {C}}}\mathcal{N}}}\left( {0,\sigma _{\mathrm{g}}^2} \right)$. Considering that the random variable $N_k$ and $G_k$ are statistically independent, the variance of ${\tilde{N}}_k$ can be calculated as follows:

$$\begin{aligned} \begin{array}{ll} {\textit{Var}}\left( {{\tilde{N}}_k } \right) &{}= E\left[ {\left| {N_k + G_k } \right| ^2 } \right] \cdot P\left( {b_n = 1} \right) + E\left[ {\left| {N_k } \right| ^2 } \right] \cdot P\left( {b_n = 0} \right) \\ &{} = \left( {\sigma _n^2 + \sigma _g^2 } \right) \cdot p + \sigma _n^2 \cdot \left( {1 - p} \right) \\ \end{array} \end{aligned}$$

(15)

The variance of the desired signal component within the k-th sub-channel is given by:

$$\begin{aligned} {\textit{Var}}\left( {U_k } \right) = \sigma _s^2 \cdot \left| {H_k } \right| ^2 \end{aligned}$$

(16)

Combining Eq. (15) with Eq. (16), the instantaneous SINR of the conventional OFDM receiver within the k-th sub-channel is presented as follows:

$$\begin{aligned} r_{k,\mathrm{out}} = \rho _{\mathrm{OFDM}} \cdot \left| {H_k } \right| ^2 ,\quad k = 0,1,\ldots ,N - 1 \end{aligned}$$

(17)

where $\rho _{\mathrm{OFDM}} = \frac{{\sigma _s^2 }}{{\left( {\sigma _n^2 + \sigma _g^2 } \right) \cdot p + \sigma _n^2 \cdot \left( {1 - p} \right) }}$.

In the following situation, if no impulse noise is presented at the input of the OFDM receiver, i.e., $p = 0$, the instantaneous SINR expression given in Eq. (17) is then reduced to $r_{k,\mathrm{out}} = \left( {{{\sigma _s^2 } \big / {\sigma _n^2 }}} \right) \cdot \left| {H_k } \right| ^2$, which was reported in [28].

3.2 SINR of the OFDM Receiver with Ideal Blanking

Assuming the location where the impulse noise occurs in each OFDM symbol is perfectly obtained by the impulse estimator, the ideal blanking scheme can be used to mitigate the impulse interference [30]. The n-th diagonal element of the nonlinear pulse blanking matrix ${\mathbf {D}}$ is presented as follows:

$$\begin{aligned} d_n = \left\{ \begin{array}{l} 0,\mathrm{{ }}b_n = 1 \\ 1,\mathrm{{ }}b_n = 0 \\ \end{array} \right. ,\mathrm{{ }}n = 0,1,\ldots ,N - 1 \end{aligned}$$

(18)

Substituting Eq. (18) into Eq. (5), the n-th component of the signal vector ${\mathbf{y}}$ can be expressed as follows:

$$\begin{aligned} y_n = d_n \cdot \sum \limits _{l = 0}^{L - 1} {h_l x_{\left( {n - l} \right) \bmod \,N} } + d_n \cdot n_n + d_n \cdot i_n ,n = 0,1,\ldots ,N - 1 \end{aligned}$$

(19)

In Eq. (19), the first term on the righthand side is related to the desired signal and the last two terms are correlated with the AWGN and the impulse noise. Thus, Eq. (19) can be rewritten as follows:

$$\begin{aligned} y_n = \sum \limits _{l = 0}^{L - 1} {h_l x_{\left( {n - l} \right) \bmod \,N} } + {\tilde{i}}_{n,\mathrm{Blanking}} \end{aligned}$$

(20)

where ${\tilde{i}}_{n,\mathrm{Blanking}}$ represents the equivalent noise signal, which is defined as follows:

$$\begin{aligned} {\tilde{i}}_{n,\mathrm{Blanking}} = \left\{ \begin{array}{ll} - \sum \limits _{l = 0}^{L - 1} {h_l x_{\left( {n - l} \right) \bmod \,N} } ,&{}\quad b_n = 1 \\ n_n ,&{}\quad b_n = 0 \\ \end{array} \right. \end{aligned}$$

(21)

The statistical character of ${\tilde{i}}_{n,\mathrm{Blanking}}$ is presented in “Appendix 1” section. Following the N-points DFT operation, the k-th component of ${\mathbf {Y}}$ is defined as follows:

$$\begin{aligned} Y_k = X_k \cdot H_k + {\tilde{I}}_{k,\mathrm{Blanking}} ,\quad k = 0, \ldots N - 1 \end{aligned}$$

(22)

where the equivalent frequency domain noise ${\tilde{I}}_{k,\mathrm{Blanking}}$ is defined as follows:

$$\begin{aligned} {\tilde{I}}_{k,\mathrm{Blanking}} = \frac{1}{{\sqrt{N} }}\sum \limits _{n = 0}^{N - 1} {{\tilde{i}}_{n,\mathrm{Blanking}} } e^{ - 2\pi j\frac{{kn}}{N}} ,\quad k = 0, \ldots ,N - 1 \end{aligned}$$

(23)

Since the DFT operation is a unitary transformation, the variance of the equivalent frequency domain noise component ${\tilde{I}}_{k,\mathrm{Blanking}}$ is given by:

$$\begin{aligned} \begin{array}{ll} {\textit{Var}}\left( {{\tilde{I}}_{k,\mathrm{Blanking}} } \right) &{}= {\textit{Var}}\left( {{\tilde{i}}_{n,\mathrm{Blanking}} } \right) \\ &{}= p \cdot \sigma _s^2 + \left( {1 - p} \right) \cdot \sigma _n^2 \\ \end{array} \end{aligned}$$

(24)

Based on Eq. (16) and Eq. (24), the instantaneous SINR of the OFDM receiver with ideal pulse blanking within the k-th sub-channel is defined as follows:

$$\begin{aligned} r_{k,\mathrm{out}} = \rho _{\mathrm{IB}} \cdot \left| {H_k } \right| ^2 ,\quad k = 0,1,\ldots ,N - 1 \end{aligned}$$

(25)

where $\rho _{\mathrm{IB}} = {{\sigma _s^2 } \big / {\left[ {p\sigma _s^2 + \left( {1 - p} \right) \sigma _n^2 } \right] }}$.

3.3 SINR of the OFDM Receiver with Peak Value Blanking

Assuming the peak value amplitude of a received OFDM signal is accurately estimated by the impulse estimator, the peak value blanking scheme, which was reported in [22, 23], can be used to mitigate the impulse interference. The n-th diagonal element of the nonlinear pulse blanking matrix ${\mathbf {D}}$ is defined as follows:

$$\begin{aligned} d_n = \left\{ \begin{array}{l} 0,\mathrm{{ }}\left| {r_n } \right| > T_{th} \\ 1,\mathrm{{ }}\left| {r_n } \right| \le T_{th} \\ \end{array} \right. ,\quad n = 0,1,\ldots ,N - 1 \end{aligned}$$

(26)

where $T_{th}$ is the peak value threshold, which was proposed in [22, 23]. Combing Eqs. (26) and (19), the n-th component of signal vector $\mathbf{y}$ can be rewritten as follows:

$$\begin{aligned} y_n = \sum \limits _{l = 0}^{L - 1} {h_l x_{\left( {n - l} \right) \bmod \,N} } + {\hat{i}}_{n,\mathrm{Blanking}} \end{aligned}$$

(27)

where ${\hat{i}}_{n,\mathrm{Blanking}}$ represents the equivalent noise due to peak value blanking, which is defined as:

$$\begin{aligned} {\hat{i}}_{n,\mathrm{Blanking}} = \left\{ \begin{array}{ll} - \sum \limits _{l = 0}^{L - 1} {h_l \cdot x_{\left( {n - l} \right) \bmod \,N}}, &{}\quad b_n = 1,d_n = 0 \\ n_n + g_n ,&{}\quad b_n = 1,d_n = 1 \\ n_n,&{}\quad b_n = 0 \\ \end{array}\right. \end{aligned}$$

(28)

The signal vector ${\mathbf {y}}$ is further transformed into frequency domain vector ${\mathbf {Y}}$ by the N-points DFT operation, where the k-th component of ${\mathbf {Y}}$ is defined as follows:

$$\begin{aligned} Y_k = X_k \cdot H_k + {\hat{I}}_{k,\mathrm{Blanking}} \end{aligned}$$

(29)

where the equivalent frequency domain noise ${\hat{I}}_{k,\mathrm{Blanking}}$ is given by:

$$\begin{aligned} {\hat{I}}_{k,\mathrm{Blanking}} = \frac{1}{{\sqrt{N} }}\sum \limits _{n = 0}^{N - 1} {{\hat{i}}_{n,\mathrm{Blanking}} } e^{ - 2\pi j\frac{{kn}}{N}} ,\quad k = 0, \ldots ,N - 1 \end{aligned}$$

(30)

The statistical characteristics of the equivalent noise ${\hat{i}}_{n,\mathrm{Blanking}}$ are presented in [31]. For convenience, this result is repeated here as follows:

$$\begin{aligned} {\textit{Var}}\left( {{\hat{I}}_{k,\mathrm{Blanking}} } \right) = \left( {\sigma _s^2 - \sigma _n^2 - \sigma _g^2 } \right) \cdot p \cdot \exp \left( { - \frac{{T_{th}^2 }}{{2\left( {\sigma _s^2 + \sigma _n^2 + \sigma _g^2 } \right) }}} \right) + \sigma _g^2 \cdot p + \sigma _n^2 \end{aligned}$$

(31)

Using Eqs. (16) and (31), the instantaneous SINR of the OFDM receiver with peak value blanking within the k-th sub-channel is defined as follows:

$$\begin{aligned} r_{k,\mathrm{out}} = \rho _{\mathrm{PB}} \cdot \left| {H_k } \right| ^2 ,\quad k = 0,1,\ldots ,N - 1 \end{aligned}$$

(32)

where $\rho _{\mathrm{PB}} = {{\sigma _s^2 } \big / {\left[ {\left( {\sigma _s^2 - \sigma _n^2 - \sigma _g^2 } \right) \cdot p \cdot \eta + \sigma _g^2 \cdot p + \sigma _n^2 } \right] }}$ and $\eta = \exp \left( {{{ - T_{th}^2 } \big / {\left( {2\left( {\sigma _s^2 + \sigma _n^2 + \sigma _g^2 } \right) } \right) }}} \right)$ .

3.4 SINR of the OFDM Receiver with Optimum Threshold Blanking

In this section, the optimum threshold blanking scheme, which was reported in [8, 20], is used to mitigate the impulse noise. The n-th diagonal element $d_n$ of the nonlinear pulse blanking matrix ${\mathbf {D}}$ is defined as follows:

$$\begin{aligned} d_n = \left\{ \begin{array}{l} 0,\mathrm{{ }}\left| {r_n } \right| > T_{\mathrm{opt}} \\ 1,\mathrm{{ }}\left| {r_n } \right| \le T_{\mathrm{opt}} \\ \end{array} \right. ,\quad n = 0,1,\ldots ,N - 1 \end{aligned}$$

(33)

where $T_{\mathrm{opt}}$ is the optimal pulse blanking threshold. Substituting Eq. (33) into Eq. (19), the n-th component of the signal vector ${\mathbf {y}}$ is then defined as follows:

$$\begin{aligned} y_n = \left\{ \begin{array}{ll} r_n,&{}\quad \left| {r_n } \right| < T_{\mathrm{opt}} \\ 0,&{}\quad \left| {r_n } \right| \ge T_{\mathrm{opt}} \\ \end{array} \right. , \quad n = 0,1,\ldots ,N - 1 \end{aligned}$$

(34)

Using the results derived in [8, 20], Eq. (34) can be further expressed as follows:

$$\begin{aligned} y_n = \gamma u_n + {\mathop {i}\limits ^{\frown }} _{n,\mathrm{Blanking}} ,\quad n = 0,1, \ldots ,N - 1 \end{aligned}$$

(35)

where $u_n = \sum \nolimits _{l = 0}^{L - 1} {h_l \cdot x_{\left( {n - l} \right) \bmod \,N} }$ denotes the desired signal, $\gamma$ is an appropriately chosen scaling factor, and ${\mathop{i}\limits^{\frown }} _{n,\mathrm{Blanking}} = y_n - \gamma u_n$ represents the equivalent noise. The discrete channel impulsive response $h_l$ is assumed to be a constant over the duration of one OFDM symbol interval, and the discrete-time channel power is normalized to one. Therefore, $u_n$ is an i.i.d complex Gaussian random variable with a mean of zero and a variance $\sigma _s^2$, such that the scaling factor can be written as follows:

$$\begin{aligned} \gamma = \frac{{E\left[ {y_n u_n^ * } \right] }}{{E\left[ {\left| {u_n } \right| ^2 } \right] }} = \frac{1}{{\sigma _s^2 }}E\left[ {y_n u_n^ * } \right] \end{aligned}$$

(36)

The signal vector ${\mathbf {y}}$ is further transformed into frequency domain vector ${\mathbf {Y}}$ by the N-points DFT operation, where the k-th component of ${\mathbf {Y}}$ is defined as follows:

$$\begin{aligned} Y_k = \gamma U_k + {\mathop {I}\limits ^{\frown }} _{k,\mathrm{Blanking}} \end{aligned}$$

(37)

In Eq. (37), $U_k = X_k \cdot H_k$ and ${\mathop {I}\limits ^{\frown }} _{k,\mathrm{Blanking}}$ are obtained as follows:

$$\begin{aligned} {\mathop {I}\limits ^{\frown }} _{k,\mathrm{Blanking}} = \frac{1}{{\sqrt{N} }}\sum \limits _{n = 0}^{N - 1} {{\mathop {i}\limits ^{\frown }} _{n,\mathrm{Blanking}} } e^{ - 2\pi j\frac{{kn}}{N}} ,\quad k = 0, \ldots ,N - 1 \end{aligned}$$

(38)

From Eq. (37), the SINR of the OFDM receiver with optimal threshold blanking within the k-th sub-channel is defined as follows:

$$\begin{aligned} r_{k,\mathrm{out}} = \rho _{\mathrm{OB}} \cdot \left| {H_k } \right| ^2 \end{aligned}$$

(39)

where $\rho _{\mathrm{OB}} = {{\gamma ^2 \sigma _s^2 } \big / {\left( {E\left[ {\left| {y_n } \right| ^2 } \right] - \gamma ^2 \sigma _s^2 } \right) }}$ . The terms $E\left[ {\left| {y_n } \right| ^2 } \right]$ and $\gamma$ were previously derived in [8, 20]. For convenience, the expressions for these terms are defined as follows:

$$\begin{aligned} E\left[ {\left| {y_n } \right| ^2 } \right] = \sum \limits _{i \in \left\{ {I,{\bar{I}}} \right\} } {\left\{ {\sigma _i^2 - \left( {\sigma _i^2 + T_{\mathrm{opt}}^2 } \right) \cdot e^{ - \frac{{T_{\mathrm{opt}}^2 }}{{\sigma _i^2 }}} } \right\} } \cdot P\left( i \right) \end{aligned}$$

(40)

$$\begin{aligned} \gamma = \frac{1}{{\sigma _s^2 }}\left( {1 - \sum \limits _{i \in \left\{ {I,{\bar{I}}} \right\} } {\left\{ {\left( {1 + \frac{{T_{\mathrm{opt}}^2 }}{{\sigma _i^2 }}} \right) \cdot e^{ - \frac{{T_{\mathrm{opt}}^2 }}{{\sigma _i^2 }}} } \right\} } \cdot P\left( i \right) } \right) \end{aligned}$$

(41)

where I denotes an event wherein the impulse noise occurs at a probability of $p\left( I \right) = p$; ${\bar{I}}$ is the complement of event I with a probability of $P\left( {{\bar{I}}} \right) = 1 - p$; $\sigma _I^2 = \sigma _s^2 + \sigma _n^2 + \sigma _g^2$; and $\sigma _{{\bar{I}}}^2 = \sigma _s^2 + \sigma _n^2$.

4 Capacity of the OFDM System with Nonlinear Pulse Blanking

Based on the results in [33], the instantaneous capacity of the OFDM system with nonlinear pulse blanking can be written as follows:

$$\begin{aligned} C = \frac{1}{N}\sum \limits _{k = 0}^{N - 1} {\log _2 } \left( {1 + r_{k,\mathrm{out}} } \right) \end{aligned}$$

(42)

where $r_{k,\mathrm{out}}$ is the instantaneous SINR, which is defined by Eqs. (17), (25), (32), and (39), respectively. From Eq. (42), the instantaneous capacity of the OFDM system is a function of the channel frequency fading coefficients. Thus, the ergodic capacity of the OFDM system can be expressed as follows:

$$\begin{aligned} \begin{array}{ll} {\bar{C}} &{}= \int {C \cdot f({\mathbf{H}}) \cdot d{\mathbf{H}}} \\ &{}= \int {,\ldots ,} \int {\int {\frac{1}{N}\sum \limits _{k = 0}^{N - 1} {\log _2 } \left( {1 + r_{k,\mathrm{out}} } \right) \cdot f(H_0 ,\ldots ,H_{N - 1} ) \cdot dH_0 ,\ldots ,dH_{N - 1} } } \\ \end{array} \end{aligned}$$

(43)

Note that it is difficult to directly calculate the ergodic capacity based on Eq. (43). The present study first utilize the FM-EM algorithm to estimate the PDF of the instantaneous capacity of the OFDM system. The ergodic capacity and the probability of outage capacity of the OFDM system are then obtained based on the estimated PDF.

Using the results given in “Appendix 2” section, the PDF of the instantaneous capacity of the OFDM system can be approximately expressed as follows:

$$\begin{aligned} f_C \left( x \right) \approx \sum \limits _{m = 1}^M {\pi _m \left( {\frac{1}{{2\pi \sigma _m^2 }}} \right) } ^{{1/2}} \exp \left\{ { - \frac{{\left( {x - \mu _m } \right) ^2 }}{{2\sigma _m^2 }}} \right\} \end{aligned}$$

(44)

where M is the number of weighted densities, $\pi _m$ represents the weighting coefficient of the m-th component and satisfies $\sum \nolimits _{m = 1}^M {\pi _m } = 1\left( {\pi _m > 0} \right)$, and $\mu _m$ and $\sigma _m^2$ denote the mean and the variance of the m-th component, respectively. To determine the values of $\pi _m$, $\mu _m$, and $\sigma _m^2$, the famous EM algorithm is used to estimate the $3M - 1$ unknown parameters in Eq. (44). Using the PDF given in Eq. (43), the ergodic capacity of the OFDM system can be obtained as follows [34]:

$$\begin{aligned} \begin{array}{ll} E_{\mathrm{Cap}} &{}= \int _0^\infty {x \cdot f_C } \left( x \right) dx \\ \mathrm{{ }} &{}= \sum \limits _{m = 1}^M {\int _0^\infty {x \cdot \frac{{\pi _m }}{{\sqrt{2\pi } \sigma _m }}\exp \left( { - \frac{{\left( {x - \mu _m } \right) ^2 }}{{2\sigma _m^2 }}} \right) \cdot } } dx \\ \mathrm{{ }} &{}= \sum \limits _{m = 1}^M {\pi _m \left[ {\left( {\frac{{\sigma _m^2 }}{{2\pi }}} \right) ^{{1/2}} \exp \left( { - \frac{{\mu _m^2 }}{{2\sigma _m^2 }}} \right) + \mu _m \left( {1 - Q\left( {\frac{{\mu _m }}{{\sigma _m }}} \right) } \right) } \right] } \\ \end{array} \end{aligned}$$

(45)

where $Q\left( x \right)$ is the Q-function, which is defined as follows:

$$\begin{aligned} Q\left( x \right) = \int _x^\infty {\frac{1}{{\sqrt{2\pi } }}\exp \left( { - \frac{{u^2 }}{2}} \right) } du \end{aligned}$$

(46)

The probability of outage capacity is defined as the probability that the instantaneous capacity falls below the target capacity $C_{th}$. Following the mathematical manipulation and usage of the approximation defined by Eq. (44), the probability of outage capacity can be expressed as follows:

$$\begin{aligned} \begin{array}{ll} {\mathrm{P}} \left( {C_{th} } \right) &{}= \Pr \left( {C \le C_{th} } \right) \\ &{}= \int _0^{C_{th} } {f_C \left( x \right) } \cdot dx \\ &{}= 1 - \sum \limits _{m = 1}^M {\pi _m \left[ {Q\left( {\frac{{C_{th} - \mu _m }}{{\sigma _m }}} \right) + Q\left( {\frac{{\mu _m }}{{\sigma _m }}} \right) } \right] } \\ \end{array} \end{aligned}$$

(47)

5 Numerical Simulations

In this section, we provide computer simulation results to verify the accuracy of the analytical results derived by Eqs. (45) and (47).

5.1 Simulation Settings

The present study simulated an OFDM system with 512 subcarriers, a cyclic prefix length of 16, and QPSK and 16QAM modulations. The following channel models were employed: frequency-selective Rayleigh fading channels with 9 paths, frequency-selective Rician fading channels with 9 paths, and a Rician factor of 10 dB. In addition, the present study employed a Bernoulli–Gaussian impulse noise model. Four impulse mitigation schemes, specifically the conventional method, ideal pulse blanking, peak value blanking, and optimum threshold blanking, were adopted in the OFDM receivers to eliminate the impulse noise. An ideal channel estimation was assumed, and the linear zero-forcing equalizer was used to compensate for the channel distortion. In addition, the theoretical ergodic capacity and the probability of the outage capacity of the OFDM system with nonlinear pulse blanking were obtained as follows. First, the given parameter and input SNR were applied to calculate the instantaneous SINR by Eqs. (17), (25), (32), and (39). The instantaneous capacity was then obtained by Eq. (44). Afterwards, the weighting coefficients $\pi _m$, means $\mu _m$, and variances $\sigma _m^2$ were calculated by Eqs. (51), (53), and (54). Finally, the ergodic capacity and the probability of the outage capacity were calculated by Eqs. (45) and (47), respectively.

5.2 Frequency-Selective Rayleigh Fading Channels

Fig. 2

The approximate PDF of the instantaneous capacity of the OFDM system with ideal blanking over Rayleigh fading channels (${\mathrm{SNR}}=30$ dB, ${\mathrm{SIR}}=-10$ dB, and $p = 10^{ - 2}$)

Figure 2 presents the approximate PDF of the instantaneous capacity of the OFDM system with ideal blanking over Rayleigh fading channels (SNR = 30 dB, ${\mathrm{SIR}}=-10$ dB, and $p = 10^{ - 2}$). The red line represents the calculated PDF by the FM-EM algorithm, and the blue curve represents the calculated PDF based on the histogram estimation method [35]. The calculated PDF is obtained using ten normal PDFs in the FM model. And the termination condition of the EM algorithm is set to $10^{-3}$. The initial vector ${\varvec{\Theta }}_0$ is randomly generated, but the weighting coefficients must satisfy $\sum \nolimits _{k = 1}^M {\pi _k } = 1\left( {\pi _k > 0} \right)$.The PDF curve from the FM-EM algorithm agrees with the histogram estimation method.

Fig. 3

Ergodic capacity of the OFDM system with ideal pulse blanking over Rayleigh fading channels (${\mathrm{SIR}}=-10$ dB)

Figure 3 presents the ergodic capacity of the OFDM system with ideal pulse blanking over the frequency-selective Rayleigh fading channels (${\mathrm{SIR}}=-10$ dB), wherein the impulse occurrence probability p was set to 0, $10^{-4}$, $10^{-3}$, and $10^{-2}$. Two kinds of curves are presented in Fig. 3, wherein the curves marked as “MO” were generated by the Monte Carlo simulations and the curves marked as “FM” were generated by the FM-EM algorithm. Based on these curves, the following results were observed: (1) the theoretical ergodic capacity obtained by the FM-EM algorithm agrees with the Monte Carlo simulation results; and (2) the ergodic capacity of the OFDM system with ideal pulse blanking tended to decrease following an increase in the impulse occurrence probability because the ideal pulse blanking method completely mitigated the impulse noise and resulted in the mitigation of useful signals. Hence, an increase in the occurrence probability of the impulse noise increased the loss of useful signal energy, thereby resulting in an increased loss of channel capacity.

Figure 4 presents the ergodic capacity of the OFDM system with peak value blanking over the frequency-selective Rayleigh fading channels (${\mathrm{SIR}}=-10$ dB). The impulse occurrence probability p is also set to 0, $10^{-3}$, $10^{-4}$, and $10^{-2}$. The dashed curves were obtained by the Monte Carlo simulations and the solid curves were obtained by the FM-EM algorithm. The following results were observed: (1) the ergodic capacity of the OFDM system with peak value blanking tended to decrease following an increase in the impulse occurrence probability, which is similar to the ideal pulse blanking method; and (2) under the same interference condition, the ergodic capacity of the OFDM system with QPSK modulation was higher than that of the OFDM system with 16QAM modulation because the peak value of the OFDM symbol in the QPSK modulation was lower than the 16QAM modulation. As a result, the energy of the residual impulse noise in the nonlinear OFDM system with 16QAM modulation was more than that of the QPSK modulation.

Fig. 4

Ergodic capacity of the OFDM system with peak value blanking over Rayleigh fading channels (${\mathrm{SIR}}=-10$ dB)

Figures 5 and 6 present the ergodic capacity and the probability of the outage capacity of the OFDM system with different blanking schemes over the frequency-selective Rayleigh fading channels (QPSK, ${\mathrm{SIR}}=-10$ dB, and $p=10^{-2}$). A comparison of these curves from the aspect of the ergodic capacity and the outage capacity probability characterized ideal pulse blanking as the best impulse mitigation scheme. Optimum threshold blanking and peak value blanking were characterized as the second and third best schemes, respectively.

Fig. 5

Ergodic capacity of the OFDM system with different blanking methods over Rayleigh fading channels (QPSK, ${\mathrm{SIR}}=-10$ dB, and $p=10^{-2}$)

Fig. 6

Probability of outage capacity of the OFDM system with different blanking methods over Rayleigh fading channels (QPSK, ${\mathrm{SIR}}=-10$ dB, and $p=10^{-2}$)

5.3 Frequency-Selective Rician Fading Channels

Fig. 7

Ergodic capacity of the OFDM system with different blanking schemes over Rician fading channels (QPSK, ${\mathrm{SIR}}=-10$ dB, $K_\mathrm{Rice}=10$ dB, and $p=10^{-2}$)

Fig. 8

Probability of outage capacity of the OFDM system with different blanking schemes over Rician fading channels (QPSK, ${\mathrm{SIR}}=-10$ dB, $K_\mathrm{Rice}=10$ dB, and $p=10^{-2}$)

Figures 7 and 8 present the ergodic capacity and the probability of outage capacity of the OFDM system with different blanking schemes over frequency-selective Rician fading channels (QPSK, ${\mathrm{SIR}}=-10$ dB, $K_{Rice}=10$ dB, and $p=10^{-2}$). The dashed curves were derived from the Monte Carlo simulation and the solid curves were obtained by the FM-EM algorithm. The following two results were observed based on the presented curves: (1) the theoretical results were well in agreement with the simulation results; and (2) from the aspect of the ergodic capacity and the outage capacity probability, ideal pulse blanking was deemed the best impulse mitigation scheme. Optimum threshold blanking and peak value blanking were characterized as the second and third best schemes, respectively.

6 Conclusions

The present study derived the ergodic capacity and the outage capacity probability of an OFDM system with nonlinear pulse blanking by the FM-EM algorithm. Computer simulation results were generated to verify the correctness of the theoretical formulas. From our research, the following conclusions were obtained: (1) nonlinear pulse blanking schemes resulted in a loss of channel capacity compared with the conventional OFDM receiver and (2) in terms of the ergodic and outage capacity, ideal pulse blanking was characterized as the best impulse blanking scheme. In addition, optimum threshold blanking was deemed the second scheme, whereas peak value blanking was characterized as the worst scheme.

Appendices

Appendix 1: The Variance of Equivalent Noise in Eq. (21)

Considering the discrete channel impulse response $h_l$ is assumed to be a constant over the duration of one OFDM symbol interval, wherein the channel power is normalized to one. Thus, $\sum \nolimits _{l = 0}^{L - 1} {h_l x_{\left( {n - l} \right) \bmod \,N} }$ is an i.i.d. complex Gaussian random variable with a mean of zero and a variance $\sigma _s^2$. Note that $n_n \sim {{{\mathcal C}{{\mathcal {N}}}}}\left( {0,\sigma _n^2 } \right)$, the variance of the equivalent noise, can be obtained as follows:

$$\begin{aligned} \begin{array}{ll} {\textit{Var}}\left( {{\tilde{i}}_{n,\mathrm{Blanking}} } \right) &{}= E\left[ {\left| {u_n } \right| ^2 } \right] \cdot P\left( {b_n = 1} \right) + E\left[ {\left| {n_n } \right| ^2 } \right] \cdot P\left( {b_n = 0} \right) \\ &{} = p \cdot \sigma _s^2 + \left( {1 - p} \right) \cdot \sigma _n^2 \\ \end{array} \end{aligned}$$

(48)

Appendix 2: Finite Mixture (FM) with Expectation–Maximization (EM) Algorithm

In the FM model, the PDF $f_X \left( x \right)$ of a random variable X is modeled as a weighted sum of the G numbers of PDFs and can be expressed as follows [36, 37]:

$$\begin{aligned} f_X \left( {\left. x \right| {\varvec{\Theta }}} \right) \simeq \sum \limits _{k = 1}^G {\pi _k } \varPhi _k \left( {x;\,\theta _k } \right) \end{aligned}$$

(49)

where $\pi _k$ represents a weighting coefficient of the k-th term and satisfies $\sum \nolimits _{k = 1}^G {\pi _k } = 1\left( {\pi _k > 0} \right)$, ${\varvec{\Theta }} = \left( {\pi _1 ,\pi _2 , \ldots ,\pi _G ,{\varvec{\theta }}_1 ,{\varvec{\theta }}_2 , \ldots ,{\varvec{\theta }}_G } \right)$ is the vector containing all the unknown parameters in the presented FM model, and $\varPhi _k \left( {x;\,{\varvec{\theta }}_k } \right)$ denotes the k-th term using the presented normal PDF. Thus, $\varPhi _k \left( {x;\,{\varvec{\theta }}_k } \right)$is defined as follows:

$$\begin{aligned} \varPhi _k \left( {x;{\varvec{\theta }}_k } \right) = \left( {\frac{1}{{2\pi \sigma _k^2 }}} \right) ^{{1/2}} \exp \left( { - \frac{{\left( {x - \mu _k } \right) ^2 }}{{2\sigma _k^2 }}} \right) \end{aligned}$$

(50)

where ${\varvec{\theta }}_k = \left( {\sigma _k^2 ,\mu _k } \right)$ such that $\mu _k$ and $\sigma _k^2$ represent the mean and variance, respectively. To estimate the unknown parameters ${\varvec{\Theta }}$, the present study apply the famous EM algorithm [36]. However, prior to the use of the EM algorithm, the following conditions must be given: (1) the number of terms in the FM model; (2) an initial estimate of the parameters ${\varvec{\Theta }}_0$; and (3) the termination condition of the EM algorithm. Once the initial conditions are given, the iterative EM updating equations can be used to update the parameters. These equations are presented as follows.

The updating equation of $\pi _k$ is defined as follows:

$$\begin{aligned} \pi _k^{\left( {t + 1} \right) } = \frac{{\sum \nolimits _{i = 1}^K {\tau _{i,k}^{\left( t \right) } } }}{K} \end{aligned}$$

(51)

where $\pi _k^{\left( {t + 1} \right) }$ denotes the $(t+1)$-th estimated weighting coefficient; K is the total number of sample points; and $\tau _{i,k}^{\left( t \right) }$ is the t-th estimated posterior probability that the sample point $x_i$ belongs to for the k-th term and can be calculated as follows:

$$\begin{aligned} \tau _{i,k}^{(t)} = \frac{{\pi _k^{(t)} \varPhi _k \left( {x_i \left| {\theta _k^{\left( t \right) } } \right. } \right) }}{{\sum \nolimits _{k = 1}^g {\pi _k^{(t)} \varPhi _k \left( {x_i \left| {\theta _k^{\left( t \right) } } \right. } \right) } }},\quad k = 1,2, \ldots ,G,\quad i = 1,2, \ldots ,K \end{aligned}$$

(52)

The updated equation of $\mu _k$ is derived as follows:

$$\begin{aligned} \mu _k^{\left( {t + 1} \right) } = \frac{{\sum \nolimits _{i = 1}^K {\tau _{i,k}^{(t)} } x_i }}{{\sum \nolimits _{i = 1}^K {\tau _{i,k}^{(t)} } }} \end{aligned}$$

(53)

The updated equation to estimate $\sigma _k^2$ is expressed as follows:

$$\begin{aligned} \sigma _k^{2\left( {t + 1} \right) } = \frac{{\sum \nolimits _{i = 1}^K {\tau _{i,k}^{\left( t \right) } } \left( {x_i - \mu _k^{\left( t \right) } } \right) ^2 }}{{\sum \nolimits _{i = 1}^K {\tau _{i,k}^{\left( t \right) } } }} \end{aligned}$$

(54)

Thus, the EM algorithm used to estimate ${\varvec{\Theta }}$ is defined by the following steps:

• 1. Determine the number of the weighted PDFs in the FM model.

• 2. Initialize the vector ${\varvec{\Theta }}$.

• 3. Update $\pi _k$, $\mu _k$, and $\sigma _k^2$ using Eqs. (51), (53), and (54), respectively.

• 4. Repeat step 3 until the termination condition of the EM algorithm is fulfilled.