1 Introduction

Seawater intrusion (SWI) poses a significant threat to the livelihood of populations in coastal zones who are dependent on freshwater extracted from aquifers near to the sea. The sustainable management of coastal aquifers is crucial to prevent the degradation of freshwater resources by the landward intrusion of seawater due to over-pumping and the detrimental effects of climate change. Difficulties arise when modeling the extent of SWI given the inherent heterogeneity present in most coastal aquifers, which can significantly affect the flow and transport properties of the system.

Nowadays, problems of SWI in coastal aquifers are commonly investigated using sandbox-based laboratory experiments, which give insight into hydrodynamic processes and provide benchmarks for numerical model calibrations. Image analysis, which uses a calibration model to relate the captured image property (light intensity) to the desired system property (concentration), has been widely used to track the migration of contaminants in groundwater flow using sandbox style experiments (Schincariol and Schwartz 1990; Goswami and Clement 2007; Chang and Clement 2013, Konz et al. 2009; Dose et al. 2014. It provides several advantages over traditional sensor array setups, most notably the lack of invasive sampling instrumentation affecting the flow path and the increased information attained from higher spatial resolutions. However, most of the experiments based on image analysis considered only homogeneous porous media cases and assumed a sharp interface between the two interacting fluids (saltwater and freshwater). Furthermore, the image analysis carried out in these studies was largely qualitative and consisted of tracing the saltwater-freshwater interface visually.

Recently, Robinson et al. (2015) proposed an automated image analysis approach based on a pixel-wise regression method, which provided low errors in converting light intensity to concentration, and allowed for the analysis of density variations across the saltwater-freshwater interface. The main disadvantage of the pixel-wise regression method is that the calibration is entirely specific to the test domain. A new calibration was required for each test case, even for homogeneous cases of the same bead diameter. In the case of Robinson et al. (2015) the calibration process took at least 4 h to complete, and contributed significantly to the 7–12 h required for preparing each domain for testing. For larger scale experiments the calibration process could be considerably longer. Furthermore, Robinson et al. (2015) observed significant air pockets accumulating within a saturated sandbox of porous media that was left for an extended period of time. Air pockets appear as dark spots in the captured images and introduce errors into the image light intensity to concentration conversion. Therefore longer calibration procedures would increase the chance of air bubbles forming in the domain and could detrimentally affect the observations. A calibration methodology that could be universally applied to all domains, irrespective of heterogeneous structure, would significantly reduce the time required for testing and decrease image distortion by trapped air pockets. In heterogeneous aquifers the different bead sizes have different refraction indices and thus appear darker or lighter in the camera images. In order to account for these variations in light intensity more sophisticated regression methods are required.

Machine Learning Techniques (MLTs) have been widely used to detect patterns in data and make predictions based on the discovered patterns (Murphy 2012). The Random Forest method is an MLT which utilises numerous decision trees to construct a predictor ensemble for regression analysis (Breiman 2001). This study investigated the application of MLTs, in particular the Random Forest method, as an advanced calibration method for image analysis, in order to improve the efficiency of conducting sandbox-style experiments. The method is applied to a variety of experimental cases including homogeneous and heterogeneous configurations and the corresponding results were contrasted with those obtained using pixel-wise regression method (Robinson et al. 2015). The Random Forest method proves to save significant preparation time by generating a calibration that is applicable to all heterogeneous configurations, negating the need to run individual calibrations for each case. Furthermore, the method showed promising results in terms of its robustness to measurement error and its ability to efficiently process large-scale experiments without increasing the errors in the estimation of saltwater intrusion parameters.

2 Experimental Set-up

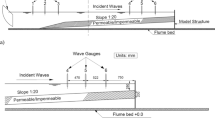
The experimental investigation was conducted within a sandbox apparatus, whose schematic diagram is depicted in Fig. 1. The tank comprised a central viewing chamber of dimensions (Length × Height × Depth) 0.38 m × 0.15 m × 0.01 m with two large chambers at either side providing the hydrostatic pressure boundary conditions for each test. The central viewing chamber (test area) was filled with a clear porous media (glass beads) to allow visual observations of salt-water movement within the aquifer. The media was retained in the viewing chamber by fine mesh screens. The left side chamber was assigned to hold clear freshwater and the right side chamber contained a dyed saltwater solution. Water levels were maintained in the side chambers through adjustable overflow outlets. The 2D nature of this unit allowed for a transmissive lighting configuration to be employed, permitting image capture and analysis of the mixing zone dynamics. Two LED array light sources provided the backlighting, which was passed through a diffuser before entering the rear of the tank. The extent of intrusion was controlled by varying the hydraulic gradient across the porous media using the adjustable overflow outlets. A range of head difference (dH) conditions were tested, ranging from 4 to 6 mm. Such fine differences produced substantial saltwater wedge movement at this scale. Ultrasonic sensors were used to accurately measure the water levels in the side chambers. Further details regarding the experimental set-up can be found in Robinson et al. 2015.

Fig. 1
figure 1

Schematic diagram of the sandbox experiment tank, front (top) and plan (bottom) elevation

Full size image

3 Calibration Using Random Forest

Image analysis requires a calibration to relate the captured image property (light intensity) to the desired system property (concentration). This relationship is non-linear and has been represented by a range of equations in the published literature (Goswami and Clement 2007; McNeil et al. 2006). In order to capture this complex relationship, this study investigates the application of the Random Forest method, as a calibration model.

3.1 Random Forest Method

Random Forest is an MLT, for building a predictor ensemble with a set of decision trees constructed by injecting randomly into the training. Decision Trees are a non-parametric supervised learning method, which aims to predict the value of a target variable by learning simple decision rules inferred from the data features. The corresponding models are obtained through a recursive partitioning of the features space and then fitting a simple prediction model within each partition. The most popular decision tree algorithms C4.5 Algorithm (Quinlan 1993) and CART (Classification and Regression Trees) Algorithm (Breiman et al. 1984). Although decision trees are relatively simple to understand and interpret, and do require distributional assumption on the predictive and response variables, their major deficiencies include the over-fitting, i.e. the constructed tree can be pretty accurate on the training dataset but very poor for prediction on unseen data; and the instability, i.e. a little variation in the data might lead to a completely different tree being generated.

3.1.1 Random Forest: Basic Principle

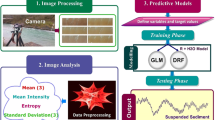
The motivation behind the Random Forest approach is to mitigate some of the major deficiencies of decision trees including prediction accuracy, over-fitting and instability, through an ensemble of decision trees. The approach originated from a series of research works by Breiman (1996, 2001), which highlighted the significant improvement in predictive accuracy that could be achieved in regression and classification by using an ensemble of trees, where each tree in the ensemble, also referred to as a weak learner, is constructed by introducing some randomness into the learning process so that the ensemble consists of set of diverse trees from the same dataset. Figure 2 shows a flow chart summarising the processes involved in the Random Forest model.

Fig. 2
figure 2

Flow chart describing the process of the Random Forest algorithm

Full size image

3.1.2 Advantages and Limitations of Random Forest

In addition to its predictive accuracy, some of the main advantages of the Random Forest model include its ability to capture nonlinear complex relationships between the predictive and response variables, it is generally not prone to over fitting as well as its robustness with regard to outliers and spurious data. Unlike other machine learning techniques (such as Artificial Neural Networks or Support Vector Machines), Random Forest requires mainly two parameters, namely the number of trees and the number of features to be selected randomly at each node for the splitting process. Furthermore, the Random Forest method is computationally lighter than most of its competitors; thus it runs efficiently on datasets with large number of predictive variables. On the other hand, one of the main deficiencies of Random Forest is that for regression problems, it cannot predict a value of the response variable beyond the range in the training data.

Random forest is widely used for in image analysis in computer science and some of its successful applications in the literature, include (Stefanski et al. 2013) and (Lowe and Kulkarni 2015).

3.2 Calibration Methodology

In order to correlate image light intensity to concentration a series of reference images at different concentrations are required. For this study, 8 different known concentrations of saltwater solution were flushed through each test case aquifer: 0%, 5%, 10%, 20%, 30%, 50%, 70% and 100%. To decrease the potential for trapping air in the pores of the porous media the glass beads were introduced through a siphon, maintaining fully saturated conditions during placement. An image was taken of the aquifer to represent the initial conditions or 0% concentration in the calibration. The aquifer was then fully flushed with 5% concentration by introducing the saltwater solution at the bottom of the side chambers and displacing the lighter, less dense solution out through the overflow (Fig. 3). By this mechanism it was possible to maintain fully saturated conditions throughout the calibration. This process was repeated until the images for all 8 different concentrations were acquired. The test aquifer was then reset to the initial conditions by diluting the saltwater in the side chambers with large quantities of clear freshwater. Residual saltwater was tapped off from the bottom of the side chambers. This part of the procedure was arguably the most time consuming as it was imperative that all the saltwater was flushed out of the system before initiating any test cases. Test cases were conducted by introducing 100% saltwater solution to one of the side chambers to displace the existing freshwater and imposing a hydraulic gradient across the aquifer by adjusting the levels of the overflows. Both freshwater and saltwater were continually introduced into their respective side chambers to maintain the imposed hydraulic gradient. Images were then captured of the saltwater wedge at regular intervals as it transitioned through the porous media until reaching a steady-state condition. Steady-state was said to be achieved when no significant movement was observed at the toe of the saltwater wedge.

Fig. 3
figure 3

Flow chart describing the methodology to acquire images from physical testing to be used in the calibration of image light intensity to concentration

Full size image

Many variants of the Random Forest model have been implemented in machine learning toolboxes available in various software packages such as MATLAB (Matlab and Statistics Toolbox (2014)), R (R Development Core Team (2017)) and Python (Scikit-learn developers (2017)). For our numerical experiments, we use the Random Forest variant implemented in MATLAB (Matlab and Statistics Toolbox (2014)).

In order for the Random Forest model to perform optimally, the model was trained on calibration images captured using exactly the same camera settings (exposure, rate, gain etc.). The model was trained on 3 homogeneous cases, where each case was constructed using a different diameter of glass bead (780 μm, 1090 μm, 1325 μm) so that the model would be representative of all bead sizes used in the heterogeneous cases. Including all 3 bead diameters in the training allowed the model to account for the different refraction indices of the media and the associated changes in light intensity produced in the captured images. The results of the trained model were applied to 2 heterogeneous cases: 1) a domain consisting of different diameter beads in layers (Layered-1); 2) a domain consisting of blocks of different diameter beads (Blocked-1). Images of the fully flushed domains at 8 different known saltwater concentrations were analysed. Within each homogeneous case, two thirds of the pixel data was used to train the model with the remaining third used for verification (out of bag elements – see Fig. 2). The fully trained model was then used to derive saltwater concentration from the captured images during testing.

4 Results and Discussion

Figure 4 shows the comparison between the output from the pixel-wise regression and Random Forest methods for the 780 μm steady-state dH = 4 mm case. The general shape and extent of the intruded saltwater wedge is captured by the Random Forest method (Fig. 4c) However, where the pixel-wise method shows good uniformity of concentration distribution in the fully freshwater and saltwater zones, the Random Forest method shows significant variation. This is due to the non-uniform light distribution provided by the 2 LED lights used to illuminate the domain. The middle of the test chamber appeared lighter than the edges, resulting in the Random Forest method calculating higher concentrations at the edges than in the middle. This is apparent in both the freshwater region (top right/left of Fig. 4c) and within the saltwater wedge (bottom middle of Fig. 4c). The results from the Random Forest method could be improved with a concerted effort to minimise non-uniform lighting across the domain.

Fig. 4
figure 4

Saltwater concentration fields determined from the pixel-wise and random forest calibrations for the steady-state dH = 4 mm 780 μm case

Full size image

The results for the homogeneous 1090 μm and 1325 μm domains are presented in Figs. 5 and 6 respectively. The effects of the non-uniform lighting are also observed in these two cases. These effects become problematic when quantifying the toe length (TL) and the width of the mixing zone (WMZ). The TL is defined as the horizontal distance between the saltwater boundary and the location of the 50% concentration isoline as it intersects the bottom boundary. The WMZ is defined as the vertical distance between the 25% and 75% concentration isolines averaged along the horizontal length of the saltwater wedge. The brighter area around the middle of the domain results in the Random Forest method assigning lower concentrations of saltwater in this area compared to the pixel-wise method. This apparent dilution of saltwater occurs at the toe of the intruding wedge, distorting the 50% concentration isoline used to calculate the TL. Furthermore, the diluted area produces an expanded mixing region, artificially increasing the WMZ. The 1325 μm bead case shows the greatest variation in light intensity distribution across the domain (Fig. 6). This is reflected in the concentration fields calculated by both the pixel-wise and Random Forest methods, which show larger and more frequent variations compared to the other homogeneous bead cases.

Fig. 5
figure 5

Saltwater concentration fields determined from the pixel-wise and random forest calibrations for the steady-state dH = 4 mm 1090 μm case

Full size image
Fig. 6
figure 6

Saltwater concentration fields determined from the pixel-wise and random forest calibrations for the steady-state dH = 4 mm 1325 μm case

Full size image

The results from the heterogeneous cases are shown in Figs. 7 and 8 for the Layered and Blocked cases respectively. From visual inspection, the saltwater wedge is clearly identifiable. However, Fig. 7b shows significantly high saltwater concentration in the upper layer (1325 μm) of the Layered case. A particularly high saltwater concentration was observed in the top right corner, which should only contain freshwater. Furthermore, the area of the concentration discrepancy extends into the upper portion of the saltwater wedge, artificially increasing the thickness of the mixing zone in this region. The concentration prediction in the lower layer (780 μm) is much more realistic, with peaks of 12% saltwater concentration in the freshwater region. The saltwater concentration difference (∆C) highlights the discrepancies between the Random Forest and pixel-wise methods, determined by:

$$ \Delta C=\left|{C}_{PW}-{C}_{RF}\right| $$
(1)

where C PW and C RF are the pixel-wise and Random Forest concentration predictions respectively. The spatial distribution of ∆C is shown in Fig. 7c for the Layered case. It is clear that the greatest variations occur along the saltwater-freshwater interface and within the upper 1325 μm layer. The Blocked case shows much less variation across the domain compared to the Layered case, as shown in Fig. 8b. The individual blocks of different bead diameters are still identifiable from the concentration field plot. However, the magnitude of the variations in the 1325 μm zones show significant reduction in ∆C compared to the Layered case (Fig. 8c). Similar to the Layered case, the variation is largest along the saltwater-freshwater interface. This becomes problematic when quantifying both the TL and WMZ. The mean and standard deviation ∆C for each test case is summarised in Table 1. On average, the Layered case showed the most variation, followed by the 1325 μm case. For this bead size, the formation of trapped air pockets occurred much faster compared to the smaller bead sizes. The air bubbles act to reduce the light intensity of affected pixels, and the calibration methods would artificially increase the concentration in these locations. Hence, the underperformance of the Random Forest method may be attributed to these air bubbles.

Fig. 7
figure 7

Results from the Layered steady-state dH = 6 mm case, including: (a.) processed camera image for analysis, (b.) Random Forest concentration field, and (c.) concentration field difference between Random Forest and pixel-wise methods

Full size image
Fig. 8
figure 8

Results from the Blocked steady-state dH = 6 mm case, including: (a.) processed camera image for analysis, (b.) Random Forest concentration field, and (c.) concentration field difference between Random Forest and pixel-wise methods

Full size image
Table 1 Summary of the concentration difference ∆C statistics between the Random Forest and pixel-wise calibration methods
Full size table

The quantification of SWI parameters is an integral part of the automated image analysis procedure developed in (Robinson et al. 2015). Therefore, the output from the procedure is a key factor in assessing the accuracy of the Random Forest method compared with the pixel-wise method. The routines to calculate the TL and WMZ were run on the concentration fields calculated by the Random Forest method and compared to the pixel-wise method. The results are summarised in Table 2, where:

$$ dTL={TL}_{PW}-{TL}_{RF} $$
(2)
$$ dWMZ={WMZ}_{PW}-{WMZ}_{RF} $$
(3)
Table 2 Summary of the toe length and width of mixing zone differences between the Random Forest and pixel-wise calibration methods
Full size table

As expected, the largest variations occur in the cases where 1325 μm beads constituted a significant proportion of the aquifer, most notably, in the homogeneous 1325 μm and Layered cases (Table 2). The TL appears to be captured reasonably well by the Random Forest model, with the largest variation of 11 mm (7% difference compared to pixel-wise method) occurring in the 1325 μm case. The difference can be attributed to the apparent dilution of saltwater concentration at the toe due to the non-uniform light distribution. The heterogeneous cases use the dH = 6 mm steady-state images, where the wedge has not intruded far enough into the aquifer for the TL to be affected by the non-uniform light distribution, and therefore show a small variation of 2-3 mm (3% difference). Conversely, the Random Forest WMZ shows significant deviation from those obtained using the pixel-wise method. Increases in WMZ of up to 100% were observed for the 1325 μm case. In general, the WMZs for the Random Forest method were larger than those given by the pixel-wise method, which can be attributed to the concentration variation observed along the saltwater-freshwater interface (e.g. Fig. 7c and 8c). Furthermore, the increased variation in the concentration field makes it more difficult for the automated routines to identify the most representative concentration isolines (Robinson et al. 2015). The Blocked Random Forest WMZ compared reasonably well with results obtained using the pixel-wise method, with a variation of only 0.3 mm, which is around the same size as a single pixel.

To more clearly observe the differences between the pixel-wise and Random Forest methods, vertical concentration sampling lines were taken at various locations along the 1325 μm case (Fig. 9a). Sampling lines were selected within 3 key regions of the aquifer: (1) the fully freshwater zone (Fig. 9b), (2) the location of the intrusion toe (Fig. 9c) and (3) within the boundaries for WMZ calculation (Fig. 9d). A moving average filter (5 pixels) was applied to the concentration values along the sample lines to reduce noise and more clearly show the differences. At all 3 sample locations, the effect of the non-uniform backlighting can be observed by the apparent increase in concentration at the top of the image for the Random Forest results when compared to pixel-wise method (Fig. 9d). For sample line 2, at the intrusion toe Fig. 9c), the Random Forest saltwater concentration at the bottom fluctuates around 55%, while the pixel-wise concentration varies around 95%. As discussed previously, the TL is quantified by finding the intersection of the 50% saltwater concentration isoline with the bottom boundary of the aquifer. The apparent dilution of saltwater concentration observed in the Random Forest results would make it difficult for the automated analysis routine to determine the most representative 50% concentration isoline, resulting in an artificial reduction in TL. On the other hand, this apparent dilution has the added effect of artificially increasing the WMZ. Fig. 9d shows the saltwater concentration along a sample line taken within the boundaries used for quantification of WMZ. While the location of the 25% concentration value is similar for both pixel-wise and Random Forest methods (Z25 = 0.024 m), the location of the 75% concentration value is quite different. The pixel-wise regression method shows Z75 = 0.020 m, resulting in WMZ = 4 mm, while the Random Forest method gives Z75 = 0.004 m, equating to WMZ = 20 mm. At face value, this increase seems substantial, but the apparent dilution caused by the non-uniform light distribution is restricted to primarily around the toe location and at the saltwater boundary. In fact, the large discrepancy was partly averaged out by the sampling along the rest of saltwater-freshwater interface, a shown in Table 2 (dWMZ = 4 mm). Although this difference is still significant for experiments at this scale, it may not be as important in larger scale tests.

Fig. 9
figure 9

Vertical saltwater concentration profiles through the steady-state dH = 4 mm 1325 μm case, comparing the Random Forest (RF) and pixel-wise (PW) methods, where, (a.) RF concentration colourmap with annotated sample lines, (b.), (c.) and (d.) are saltwater concentrations (C) along sample lines 1, 2 and 3 respectively

Full size image

Although generally considered as a deficiency of the Random Forest method, the inability of the method to predict a value of concentration beyond the range of the training data is advantageous in that at no stage was a pixel assigned a saltwater concentration higher than 100% or lower than 0%. On a number of occasions, the pixel-wise method predicted concentrations marginally higher than 100%, especially along the bottom boundary of the aquifer (Fig. 9c and d). The Random Forest method is also advantageous in that the images do not have to be perfectly synchronised in space. For the pixel-wise method, extreme care was required to not disturb the camera during testing to reduce the risk of introducing errors from desynchronised images. The improved efficiency of the Random Forest model provided time savings of around 35% for this experimental setup. It is expected that the time savings would increase as the scale of the experiment increases.

5 Summary and Conclusions

This study introduced a calibration approach that could relate light intensity to concentration for image analysis of laboratory-scale sandbox experiments using the Random Forest method (Breiman 2001). The goal of the study was to develop a unified calibration methodology that could be applied to a wide range of experiments using different grain diameters and heterogeneous configurations, without the need to acquire specific calibration images for individual cases, thus increasing testing efficiency. The model was trained using calibration images from previous experiments, where no special measures were undertaken in the image acquisition to facilitate the model. The model was then applied to images from steady-state test cases and the results compared to those from the high resolution pixel-wise calibration method introduced in (Robinson et al. 2015). The main conclusions from the study are:

  1. 1.

    The Random Forest-based calibration model captured the general shape of the saltwater wedge and the extent of intrusion. The model was sensitive to back light distribution, where strong variations in lighting were conserved through the calibration and appeared as either artificially high or low concentration regions in the output saltwater concentration fields;

  2. 2.

    The models performance varies according to the bead diameters. The 1090 μm case showed the least variation out of the homogeneous cases, with the 1325 μm case showing significant variations at the edges of the sandbox. This was partly due to trapped air forming in the 1325 μm test case, coupled with the non-linear back light distribution;

  3. 3.

    In the heterogeneous cases, the Random Forest model performance was poor in areas constructed of 1325 μm beads, such as the upper layer in the Layered case. The greatest deviations between the Random Forest model and the pixel-wise method were observed around the edges of the sandbox and along the saltwater-freshwater interface.

  4. 4.

    The Random Forest model predicted TL well, where most cases were within a few millimetres of the pixel-wise method. The WMZ was generally larger for the Random Forest model compared with the pixel-wise method, particularly for the 1325 μm case.

The Random Forest calibration method provided promising results, especially considering the calibration images were not acquired with the process in mind. With a concerted effort to minimise non-linear light distribution, through rigorous setup of the back lights and orientation of the sandbox, the Random Forest method could provide much more accurate results than those presented in this study. The discrepancies observed in the TL and WMZ, although significant for these tests, are not expected to scale with increasing the size of the sandbox. Therefore the Random Forest method shows potential, especially considering the significant time savings, where unique calibrations for each aquifer configuration are not required. This time saving is expected to increase exponentially with increasing scale of the sandbox experiment, providing a much more efficient method of calibration for image analysis.