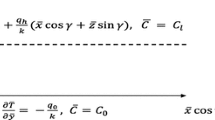On the Stability of Density Stratified Flow Below a Ponded Surface

Abstract

Flooding of coastal areas with seawater often leads to density stratification. The stability of the density-depth profile in a porous medium initially saturated with a fluid of density $\rho _\mathrm{f}$ after flooding with a salt solution of higher density $\rho _\mathrm{s}$ is analyzed. The standard convection/diffusion equation subject to the so-called Boussinesq approximation is used. The depth of the porous medium is assumed to be infinite in the analytical approaches and finite in the numerical simulations. Two cases are distinguished: the laterally unbounded ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and the laterally bounded ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$. The ratio of the diffusivity and the density difference $(\rho _\mathrm{s} - \rho _\mathrm{f})$ induced gravitational shear flow is an intrinsic length scale of the problem. In the unbounded ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$, this geometric length scale is the only length scale and using it to write the problem in dimensionless form results in a formulation with Rayleigh number $R = 1$. In the bounded ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, the lateral geometry provides another length scale. Using this geometrical length scale to write the problem in dimensionless form results in a formulation with a Rayleigh number R given by the ratio of the geometric and intrinsic length scales. For both ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, the well-known Boltzmann similarity solution provides the ground state. Three analytical approaches are used to study the stability of this ground state, the first two based on the linearized perturbation equation for the concentration and the third based on the full nonlinear equation. For the first linear approach, the surface spatial density gradient is used as an approximation of the entire background density profile. This results in a crude estimate of the $L^2$-norm of the concentration showing that the perturbation at first grows, but eventually decays in time. For the other two approaches, the full ground-state solution is used, although for the second linear approach subject to the restriction that the ground state slowly evolves in time (the so-called frozen profile approximation). Just like the ground state, the resulting eigenvalue problems can be written in terms of the Boltzmann variable. The linearized stability approach holds only for infinitesimal small perturbations, whereas the nonlinear, variational energy approach is not subject to such a restriction. The results for all three approaches can be expressed in terms of Boltzmann $\sqrt{t}$ transformed relationships between the system Rayleigh number and perturbation wave number. The results of the linear and nonlinear approaches are surprisingly close to each other. Based on the system Rayleigh number, this allows delineation of systems that are unconditionally stable, marginally stable, or transiently unstable. These analytical predictions are confirmed by direct two-dimensional numerical simulations, which also show the details of the transient instabilities as function of the wave number for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and the wave number and Rayleigh number for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$. A numerical example of the effect of a layer with low permeability is also shown. Using typical values of the physical parameters, the analytical and numerical results are interpreted in terms of dimensional length and time scales. In particular, an explicit stability criterion is given for vertical column experiments.

1 Introduction

Stability of density stratified fluids has been studied for more than 100 years. In the book ’The self-made tapestry’, Ball (2001) gives in chapter 7 a lucid description of the history of the analysis of pattern formation in such fluids. The extension to fluids in porous media is nearly as old and has been reviewed thoroughly by Straughan (2008). At first, stability was explored primarily by analytical methods applied to the linearized perturbation equations. Later it became feasible to use analytical and numerical methods to study the full nonlinear equations.

Employing those modern methods, van Duijn et al. (2002) analyzed gravitational stability of a saline boundary layer below an evaporating salt lake. They compared stability criteria obtained by three different methods: the method of linearized stability; the traditional energy method using as constraint the integrated Darcy equation; an alternative energy method using as constraint the point-wise Darcy equation. The two constraints are, respectively, referred to as integral constraint and differential constraint. They showed that the integral constraint gives a stability bound of the Rayleigh number equal to the square of the first root of the Bessel function $J_0$, in agreement with previous numerical results of Homsy and Sherwood (1976). The differential constraint gave results that were in excellent agreement with experiments by Wooding et al. (1997a, b). The stability of the saline boundary layer formed by upward flow was treated in greater detail by Pieters (2004), Pieters and Schuttelaars (2008).

In this paper, we use the same approach as in van Duijn et al. (2002) and Pieters (2004) to analyze stability following flooding with salt water of a soil initially saturated with less saline water. In the natural environment, such flooding is quite common. Marine transgression is a dominant feature of Holocene geo-hydrological history, starting almost 12 millennia ago. For example, see Raats (2015) for a historical perspective, the Dutch coastal region is shaped by marine transgression and human interference in response to this. In the region where now the freshwater IJsselmeer and the IJsselmeerpolders are located, there was in Roman times the freshwater Flevomeer, later known as Almere. Due to marine transgression, the inland lake gradually evolved into the inland Zuiderzee, which stood in open connection with the North Sea. From about 1600 AD onward, the bottom of Zuiderzee became more and more saline. With the double purpose of protection from floods and the creation of new polders, in 1932 the tidal inlet to the Zuiderzee was closed off by a dam. In a few years, the brackish Zuiderzee changed into the freshwater IJsselmeer and as a result of that the bottom started to desalinize. That process is still continuing.

Earlier studies on gravitationally unstable systems having a nontrivial base steady-state condition showed that this base condition may be unstable for a given system configuration. Perturbations to some existing condition will then lead to other nontrivial and persistent convective steady-state conditions. However, in the studies of Nield et al. (2008) and Selim and Rees (2010), as well as in the present study, the base steady-state condition only temporarily evolves to such nontrivial convective conditions. Eventually, the system will return to a new base steady-state condition which can be considered as a (concentration or temperature) redistributed version of the original base steady state. The redistributed base steady-state condition may again be unstable.

In the 1930s and early 1940s, again following Raats (2015), a group of civil engineers inspired by the mathematical physicist Burgers did pioneering work on transport of salts across the water-sediment interface. They formulated the linear convection–dispersion equation and solved this equation for appropriate boundary conditions. The calculated salinity profiles in the top 10 m were mostly in good agreement with profiles measured in the 1950s by van der Molen (see Raats 2015) and the references therein). The spatial distribution of the measured salinity profiles over a large area, such as the North–East polder, was used as an indicator of the spatial distribution of the flow velocities. However, not all field measurements were in line with the computations. In a few scattered places in the North–East polder higher salinities were found at depths of 10–15 m, far deeper than predicted and measured in other places. In some cases, this could reflect seepage of water from the former Zuiderzee to lower lying polders along the coast. In others, there was a highly permeable Pleistocene deposit reaching the surface. Van der Molen speculated that for the latter ’this phenomenon is probably due to convective currents in the bottom of the Zuiderzee between 1600 and 1931 A.D’. Specifically, he noted that the small difference in density between the freshwater present in the soil and the supernatant seawater is sufficient to cause convection currents. This is in line with the theory and computations presented in this paper.

On the timescale of centuries and under certain circumstances, marine transgression may cause rapid salinization of entire aquifers. In northwest Germany, Holocene transgressions of a few thousands of years have brought salt water of corresponding age to a depth of over 200 m (Mull and Battermanna 1980). Earlier Geirnaert (1973) had reported similar observations along the Dutch coast. In view of such results, it may seem surprising that at many other places all around the world fresh and brackish waters have been found beneath saline waters on the continental shelves (Post et al. 2013). Wherever this occurs, the deep-lying freshwater is invariably protected from invading ocean waters by sediments with a low hydraulic conductivity. Post and Simmons (2009) illustrate by means of sand tank laboratory experiments and numerical modeling how low-permeability lenses protect freshwater from mixing with overlying saline water. This is also in line with the simulations presented in this paper.

On a seasonal time scale, exchange of substances between freshwater in sediments and supernatant saline water may occur. Smetacek et al. (1976) reported that in the water of the Kiel Bight high nutrient concentrations and low oxygen concentrations were found following an influx of higher density water. They suggested that this could be related to density-induced natural convection in the sediments. Webster et al. (1996) used a computational model and laboratory experiments to demonstrate that gravitational convection can make an important contribution to the exchange of water and solutes between sediments and a supernatant water column in regions subject to significant temporal variations in salinity, such as estuaries. In effect, they verified the suggestion put forward by Smetacek et al. (1976).

In coastal regions, tsunamis often cause flooding by seawater and natural convection may then strongly contribute to the mixing of this seawater with the underlying freshwater. Illangasekare et al. (2006) described the impact of the 2004 tsunami in Sri Lanka on groundwater resources. They included results of an experiment in a 53 $\times$ 30 $\times$ 2.7 cm PlexiglasTM tank filled with glass beads. Vithanage et al. (2008) used a laboratory model to study natural convection in coastal aquifers following flooding by sea water.

The analysis of the stability of density stratified flow below a ponded surface in this paper has important connections with a pioneering paper by Wooding (1962b). In that paper, Wooding uses the method of linearized stability to analyze the behavior of an initially sharp, horizontal interface separating two miscible fluids in an infinitely long, vertical, porous column. In the upper half of the column, the fluid has a higher density than in the lower half. He studied the time dependence of the linearized equations by means of an expansion in terms of Hermite polynomials. In spite of the rather primitive numerical tools available in those days, the approach undertaken by Wooding in this and other papers—both theoretical and experimental: see, e.g., Wooding (1959, 1960, 1962a, 1969); Wooding et al. (1997a, b)—is still a source of inspiration for those studying stability problems in porous media. For this reason, we dedicate this paper in his honor.

Long before we all were made energy conscious in the 1970s, already in the mid-1950s Robin Wooding (1926–2007) was concerned with geothermal problems. He started his research in this area at the DSIR Applied Mathematics Laboratory at Wellington, New Zealand in the mid-1950s, continued it with a DSIR National Research Fellowship at Emmanuel College of the University of Cambridge. There he obtained in 1960 his Ph.D. degree under the supervision of Dr. P.G. Saffman in the group of Professor G.I. Taylor. He returned to DSIR, from where he moved in 1963 on to CSIRO at Canberra to work on overland flow and near-surface, atmospheric turbulence. On a Senior Research Fellowship, in 1968, he visited the California Institute of Technology and there he wrote (Wooding 1969). In 1970/71, he took leave without pay to spend a year at The Johns Hopkins University and the University of Wisconsin to work on flow and transport in porous media, after which he decided to return not to CSIRO but to DSIR, where he stayed until he retired in 1987. He then returned again to Canberra as Honorary Fellow at the CSIRO Pye Laboratory. There for the last two decades of his life his main interest was the salt lake problem mentioned above.

After this introduction, the outline of this paper is as follows. The mathematical model for studying the stability of density stratified flow below a ponded surface is formulated in Sect. 2, where we distinguish between laterally unconfined and confined domains. A special solution of this model is presented in Sect. 3. This solution describes the formation of a one-dimensional salt layer that penetrates into the subsurface by diffusion/dispersion. It is the main goal of this paper to investigate the gravitational (in)stability of this layer. In particular, we study the influence of the system’s dimensionless Rayleigh number and the role of time. To this end, we perturb the special solution and derive the corresponding perturbation equations. This is done in Sect. 4. Next, in Sect. 5, we investigate the stability by two different methods, namely the standard method of linearized stability, where we employ two approaches, and the energy method with differential constraint. Stability results for homogeneous soils are discussed in Sect. 6.1 and for nonhomogeneous (layered) soils in Sect. 6.2. An interpretation of the results in terms of the physical parameters of the problem is given in Sect. 7, and conclusions are presented in Sect. 8.

Remark 1

Technical details related to the stability analyses and the numerical methods are omitted in this paper. They are given in a comprehensive version of this work that appeared as the technical report Pieters et al. (2018).

2 Problem Formulation

We consider an isotropic porous medium occupying either

${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$::

the laterally unbounded half-space $\varOmega = \varOmega _A = \{z > 0\}$, or

${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$::

the three dimensional, laterally confined, semi-infinite region $\varOmega = \varOmega _B = \{(x,y,z): -L_{x,y}< x,y < L_{x,y}, z > 0\}$.

Here z is the vertical coordinate pointing downwards. We assume that the permeability $\kappa$ is constant in the x, y direction, i.e., $\kappa = \kappa (z)$ only, and that the porosity $\phi$ is constant throughout $\varOmega$.

Adopting the Boussinesq approximation (Oberbeck 1879; Boussinesq 1903; Chandrasekhar 1981; Landman and Schotting 2007), we consider the equations

$$\begin{aligned}&\displaystyle \phi \frac{\partial \rho }{\partial t} + \nabla \cdot (\mathbf{U}\,\rho ) - D\varDelta \rho = 0, \end{aligned}$$

(1a)

$$\begin{aligned}&\displaystyle -\frac{\kappa (z)}{\mu } \nabla ({\widetilde{P}}-\rho _\mathrm{f}gz )+ \frac{\kappa (z)}{\mu } (\rho -\rho _\mathrm{f}) g\mathbf{e}_z =\mathbf{U}, \end{aligned}$$

(1b)

$$\begin{aligned}&\displaystyle \nabla \cdot \mathbf{U} = 0, \end{aligned}$$

(1c)

in $\varOmega$ and for $t > 0$. In these equations, $\rho$ denotes the fluid density, $\mathbf{U}$ the Darcy velocity, and ${\widetilde{P}}$ the fluid pressure. These are the unknowns in the problem that need to be determined. The (given) physical parameters are: D (dispersion/diffusion coefficient), $\mu$ (fluid viscosity), g (gravity constant), and $\rho _\mathrm{f}$ (freshwater density). Both D and $\mu$ are assumed constant throughout this paper.

The boundary conditions at the top of the porous medium are given by:

$$\begin{aligned}&\rho = \rho _\mathrm{s} \quad \text {and} \quad {\widetilde{P}} = \rho _\mathrm{s}gh \quad \text {at }\;\; z = 0,\;\;\text {for}\;\;t > 0, \end{aligned}$$

(2a)

where $\rho _\mathrm{s}$ is the salt (sea) water density and h the height of the overlying salt water layer. Boundary condition (2a) is a simplification of what happens in practice. The laboratory experiments by Webster et al. (1996) show that growing instabilities induce local outflow from the porous medium into the ponded layer. It is assumed in this paper that outflow across the top of the porous medium $\{z = 0\}$ has no effect on the density of the fluid in the overlying layer (which is $\rho _\mathrm{s}$ for all $t > 0$).

The initial condition is given by:

$$\begin{aligned}&\rho = \rho _{i} \quad \text {in}\;\; \varOmega ,\text { at }\;t \!=\!0, \end{aligned}$$

(2b)

where the initial density satisfies $\rho _\mathrm{f} \!\leqslant \! \rho _{i} \!\leqslant \! \rho _\mathrm{s}$.

Remark 2

• (i) The results for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ can be generalized to arbitrarily shaped bounded cross sections. In Sect. 7, we consider the case of a circular cross section as well.

• (ii) Since Darcy’s law contains the gradient of the pressure, one may replace ${\widetilde{P}}$ by ${\widetilde{P}}+{\widetilde{P}}_0$, with ${\widetilde{P}}_0$ constant in space, and obtain the same discharge and salt distribution. Hence, the specific value of ${\widetilde{P}}$ at the top $z=0$ does not play a role. In other words, the discharge and salt distribution do not depend on the height h of the ponded layer. In essence, this due to the assumed constraint of incompressibility of the fluid.

It is assumed that $\rho _{i} \!\rightarrow \! \rho _\mathrm{f}$ as $z \!\rightarrow \! \infty$, implying that $\rho \!\rightarrow \! \rho _\mathrm{f}$ as $z \!\rightarrow \! \infty$ for all $t > 0$. Thus $\rho _\mathrm{f}$ acts as a far field reference value. We further assume that as $z \!\rightarrow \! \infty$, the pressure gradient force is balanced by the gravitational force. Thus, we consider those solutions of (1) that satisfy:

$$\begin{aligned}&\rho \rightarrow \rho _\mathrm{f} \quad \text {and}\quad \frac{\partial {\widetilde{P}}}{\partial z} \rightarrow \rho _\mathrm{f}g \quad \text {as}\;\; z \rightarrow \infty ,\;\;\text {for all}\;t > 0. \end{aligned}$$

(2c)

For the horizontally bounded ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, it is assumed that on lateral boundary $\varGamma _v$ (see Fig. 2) the fluxes of water and solute vanish:

$$\begin{aligned} \mathbf{U}\cdot \mathbf{n} = 0, \quad \left( \mathbf{U}\rho - D\nabla \rho \right) \cdot \mathbf{n} = 0 \quad \text {along }\;\; \varGamma _v,\;\; \text {for}\;\; t > 0, \end{aligned}$$

(2d)

where $\mathbf{n}$ is the unit vector on $\varGamma _v$.

Using the constant densities $\rho _\mathrm{s}$ and $\rho _\mathrm{f}$, we define:

$$\begin{aligned} C = \frac{\rho - \rho _\mathrm{f}}{\rho _\mathrm{s} - \rho _\mathrm{f}} \quad \text {and} \quad P = {\widetilde{P}} - \rho _\mathrm{f} g z. \end{aligned}$$

(3)

Here, P is the pressure based on the far field reference density $\rho _\mathrm{f}$. Introducing (3) into (1) and (2) gives

$$\begin{aligned}&\displaystyle \phi \frac{\partial C}{\partial t} + \nabla \cdot (\mathbf{U}\,C - D\nabla C) = 0, \end{aligned}$$

(4a)

$$\begin{aligned}&\displaystyle -\frac{\kappa (z)}{\mu } \nabla P + \frac{\kappa (z)}{\mu } (\rho _\mathrm{s}-\rho _\mathrm{f}) g C\mathbf{e}_z = \mathbf{U}, \end{aligned}$$

(4b)

$$\begin{aligned}&\displaystyle \nabla \cdot \mathbf{U} = 0, \end{aligned}$$

(4c)

subject to:

$$\begin{aligned}&\displaystyle C = C_i \quad \text {in}\;\; \varOmega ,\;\;\text { at }\;\;t=0, \end{aligned}$$

(5a)

$$\begin{aligned}&\displaystyle C = 1, \quad P= \rho _{s}gh\quad \text {at }\;\; z = 0,\;\; \text {for}\;\; t>0, \end{aligned}$$

(5b)

$$\begin{aligned}&\displaystyle C \rightarrow 0, \quad \frac{\partial P}{\partial z} \rightarrow 0 \quad \text {as}\;\; z \rightarrow \infty ,\;\; \text {for}\;\;t >0, \end{aligned}$$

(5c)

and for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ also

$$\begin{aligned}&\mathbf{U }\cdot \mathbf{n}=0, \quad (\mathbf{U}C-D\nabla C)\cdot \mathbf{n}=0 \quad \text {along }\;\; \varGamma _v,\;\;\text {for}\;\;t > 0. \end{aligned}$$

(5d)

Next, we introduce the characteristic scales for length ($L_\mathrm{c}$), time ($T_\mathrm{c}$), pressure ($P_\mathrm{c}$), discharge ($Q_\mathrm{c}$) and permeability ($\kappa _\mathrm{c} = \kappa (0)$). Using these scales, we substitute the dimensionless variables

$$\begin{aligned} (x^*,y^*,z^*) = \frac{(x,y,z)}{L_\mathrm{c}}, \quad t^* = \frac{t}{T_\mathrm{c}}, \quad P^* = \frac{P}{P_\mathrm{c}}, \quad \mathbf{U^*} = \frac{\mathbf{U}}{Q_\mathrm{c}}, \quad \kappa ^* = \frac{\kappa }{\kappa _\mathrm{c}}, \end{aligned}$$

(6)

into Eqs. (4) and conditions (5) to obtain in the scaled domain $\varOmega ^*$:

$$\begin{aligned}&\displaystyle \frac{ \phi L_\mathrm{c}^2}{T_\mathrm{c} D}\frac{\partial C}{\partial t^*} + R\nabla ^*\cdot (\mathbf{U^*}\,C) - \varDelta ^* C = 0, \end{aligned}$$

(7a)

$$\begin{aligned}&\displaystyle -\frac{\kappa _\mathrm{c}\kappa ^*(z^*)P_\mathrm{c}}{\mu L_\mathrm{c}} \nabla ^* P^* + \frac{\kappa _\mathrm{c}\kappa ^*(z^*)}{\mu } (\rho _\mathrm{s}-\rho _\mathrm{f}) g C\mathbf{e}_z =Q_\mathrm{c} \mathbf{U^*}, \end{aligned}$$

(7b)

$$\begin{aligned}&\displaystyle \nabla \cdot \mathbf{U^*} = 0, \end{aligned}$$

(7c)

subject to

$$\begin{aligned}&C = C_i \quad \text {in }\;\; \varOmega ^*,\;\; \text { at }\;\; t^*=0, \end{aligned}$$

(8a)

$$\begin{aligned}&C = 1, \quad P^* = \frac{\rho _\mathrm{s}gh}{P_\mathrm{c}} \quad \text {at}\;\; z^*= 0,\;\; \text { for }\;\; t^* >0, \end{aligned}$$

(8b)

$$\begin{aligned}&C \rightarrow 0, \quad \frac{\partial P^*}{\partial z^*} \rightarrow 0 \quad \text {as}\;\; z^* \rightarrow \infty ,\;\; \text {for}\;\;t ^*>0, \end{aligned}$$

(8c)

and for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ also

$$\begin{aligned}&\mathbf{U^*}\cdot \mathbf{n}=0, \quad (R\mathbf{U^*}C-\nabla ^* C)\cdot \mathbf{n}=0 \quad \text {along }\;\; \varGamma _v^*,\;\;\text { for }\;\; t > 0. \end{aligned}$$

(8d)

The transformed region $\varOmega ^*$ is given by

$$\begin{aligned} ({{{\mathbf {{\small {\uppercase {case~A}}}}}}})&\quad \varOmega ^*_A=\{z^*>0\}, \end{aligned}$$

(9a)

$$\begin{aligned} ({{{\mathbf {{\small {\uppercase {case~B}}}}}}})&\quad \varOmega ^*_B = \left\{ (x^*,y^*,z^*) : |x^*|< \frac{L_x}{L_\mathrm{c}}, |y^*| < \frac{L_y}{L_\mathrm{c}}, z^* > 0\right\} , \end{aligned}$$

(9b)

and in (7) and (8) the Rayleigh number R is given by

$$\begin{aligned} R = \frac{Q_\mathrm{c} L_\mathrm{c}}{D}. \end{aligned}$$

(10)

Note that in (7b) we introduced

$$\begin{aligned} \kappa ^*(z^*) = \frac{\kappa (L_\mathrm{c} z)}{\kappa _\mathrm{c}}. \end{aligned}$$

(11)

Balancing the first and third term in transport equation (7a) gives for the timescale $T_\mathrm{c}$:

$$\begin{aligned} T_\mathrm{c}=\frac{\phi L_\mathrm{c}^2}{D}, \end{aligned}$$

(12a)

and similarly, balancing all terms in Darcy’s law (7a) gives the pressure scale $P_\mathrm{c}$:

$$\begin{aligned} P_\mathrm{c}=\frac{\mu L_\mathrm{c} Q_\mathrm{c}}{\kappa _\mathrm{c}}, \end{aligned}$$

(12b)

and discharge scale $Q_\mathrm{c}$:

$$\begin{aligned} Q_\mathrm{c} = \frac{\kappa _\mathrm{c} (\rho _\mathrm{s}-\rho _\mathrm{f})g}{\mu }. \end{aligned}$$

(12c)

The discharge scale $Q_\mathrm{c}$ can be interpreted as a density difference induced, gravitational shear flow (de Josselin de Jong 1960).

The timescale $T_\mathrm{c}$ and pressure scale $P_\mathrm{c}$ are known once the length scale $L_\mathrm{c}$ has been selected. In the laterally unbounded ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$, there is no obvious length scale in terms of the spatial dimensions of the problem. Therefore, we use the intrinsic length scale $L_\mathrm{c} = D / Q_\mathrm{c}$. In the laterally bounded ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, we choose $L_\mathrm{c} = L_x / \pi$ or some other characteristic horizontal length scale. The factor $\pi$ is for notational and technical convenience. All scales are summarized in Table 1.

Table 1 Overview of the definitions of the ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ scales

For ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, the Rayleigh number is, apart from the factor $\pi$, the ratio of the characteristic geometric length scale $L_x$ and the intrinsic length scale $D/Q_\mathrm{c}$. Its value may vary considerably due to $L_x$ and, in particular, $\kappa _\mathrm{c}$ (see Sect. 7).

The scaled region $\varOmega ^*$ is given by

$$\begin{aligned} ({{{\mathbf {{\small {\uppercase {case~A}}}}}}})&\quad \varOmega ^*_A=\{z^*>0\}, \end{aligned}$$

(13a)

$$\begin{aligned} ({{{\mathbf {{\small {\uppercase {case~B}}}}}}})&\quad \varOmega ^*_B=\left\{ (x^*,y^*,z^*) : |x^*|< \pi , |y^*| < \frac{L_y}{L_x}\pi , z^* > 0\right\} . \end{aligned}$$

(13b)

Thus, after scaling, we obtain the dimensionless form of the equations, dropping the superscript *,

$$\begin{aligned}&\displaystyle \frac{\partial C}{\partial t} + R\nabla \cdot (\mathbf{U}\,C) - \varDelta C = 0, \end{aligned}$$

(14a)

$$\begin{aligned}&\displaystyle \frac{1}{\kappa (z)}\mathbf{U} = -\nabla P + C\mathbf{e}_z , \end{aligned}$$

(14b)

$$\begin{aligned}&\displaystyle \nabla \cdot \mathbf{U} = 0, \end{aligned}$$

(14c)

in $\varOmega$ and for $t > 0$, subject to

$$\begin{aligned}&C = C_i \quad \text {in}\;\; \varOmega ,\;\;\text {at}\;\;t = 0, \end{aligned}$$

(15a)

$$\begin{aligned}&C = 1, \quad P=\frac{ \rho _\mathrm{s}gh}{P_\mathrm{c}} \quad \text {at }\;\; z= 0,\;\; \text { for }\;\; t >0, \end{aligned}$$

(15b)

$$\begin{aligned}&C \rightarrow 0, \quad \frac{\partial P}{\partial z} \rightarrow 0 \quad \text {as}\;\; z \rightarrow \infty ,\;\; \text { for }\;\; t >0, \end{aligned}$$

(15c)

and for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ also

$$\begin{aligned}&\mathbf{U}\cdot \mathbf{n}=0, \quad (R\mathbf{U}C-\nabla C)\cdot \mathbf{n}=0 \quad \text {along }\;\; \varGamma _v,\text { for }t > 0. \end{aligned}$$

(15d)

The transformed region $\varOmega$ is given by

$$\begin{aligned} ({{{\mathbf {{\small {\uppercase {case~A}}}}}}})&\quad \varOmega _A=\{z>0\}, \end{aligned}$$

(16a)

$$\begin{aligned} ({{{\mathbf {{\small {\uppercase {case~B}}}}}}})&\quad \varOmega _B=\left\{ (x,y,z) : |x|< \pi , |y| < \frac{L_y}{L_x}\pi , z > 0\right\} . \end{aligned}$$

(16b)

Remark 3

Suppose one compares different values of R in ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$. These differences are due to differences in $\kappa _\mathrm{c}$ and $L_x$. Note that if $L_x$ changes, then $\kappa (z)$ changes accordingly, because of the scaling of z. This is expressed by (11). For ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$, $\kappa _\mathrm{c}$ only appears in the length scale.

Fig. 1

Ground-state profiles for various values of time

3 The Ground-State Solution

In this paper, we investigate the stability of the particular solution of (14) subject to (15) for $C_i \!\equiv \! 0$, i.e., we assume that the initial density $\rho _i$ is equal to the far field density $\rho _\mathrm{f}$. We call this particular solution the ground state and denote it by $\{C_0, U_0, P_0\}$. Because the boundary and initial conditions do not depend on the horizontal coordinates x and y, the ground state depends only on z and t. Thus $\{C_0, U_0, P_0\}$ is the solution of

$$\begin{aligned}&\displaystyle \frac{\partial C_0}{\partial t} + R\frac{\partial U_0 C_0}{\partial z} - \frac{\partial ^2 C_0}{\partial z^2} = 0, \end{aligned}$$

(17a)

$$\begin{aligned}&\displaystyle \frac{1}{\kappa (z)}U_0 = -\frac{\partial P_0}{\partial z} + C_0, \end{aligned}$$

(17b)

$$\begin{aligned}&\displaystyle \frac{\partial U_0}{\partial z}= 0, \end{aligned}$$

(17c)

subject to

$$\begin{aligned}&C_0 = 1\quad \text {and}\quad P_0 = \frac{\rho _\mathrm{s} gh}{P_\mathrm{c}} \quad \text {at }\;\; z = 0,\;\;\text { for }\;\;t > 0, \end{aligned}$$

(18a)

$$\begin{aligned}&C_0 \rightarrow 0 \quad \text { and }\quad \frac{\partial P_0}{\partial z} \rightarrow 0 \quad \text {as }\;\;z \!\rightarrow \! \infty ,\;\;\text { for }\;\;t > 0, \end{aligned}$$

(18b)

$$\begin{aligned}&C_0 = 0\quad \text {in }\;\;0< z < \infty \;\;\text {and for }\;\;t = 0. \end{aligned}$$

(18c)

Applying (18b) in (17b) shows that $U_0 = 0$ for $z \!\rightarrow \! \infty$. In view of (17c), this means that $U_0 = 0$ for all z. Using this in (17) gives:

$$\begin{aligned} \frac{\partial C_0}{\partial t}&= \frac{\partial ^2 C_0}{\partial z^2}, \end{aligned}$$

(19a)

$$\begin{aligned} \frac{\partial P_0}{\partial z}&= C_0. \end{aligned}$$

(19b)

Solving (19a) subject to (18) yields

$$\begin{aligned} C_0(z,t) = {{\mathrm{erfc}}}\left( \frac{z}{2\sqrt{t}}\right) . \end{aligned}$$

(20a)

This one-dimensional solution describes the formation of a salt layer that enters the subsurface by diffusion. Integrating (19b) subject to (18a) and (20a) results in

$$\begin{aligned} P_0(z,t) = \frac{\rho _\mathrm{s} gh}{P_\mathrm{c}} + 2\sqrt{t}\int _{0}^{\frac{z}{2\sqrt{t}}}{{\mathrm{erfc}}}(\zeta )~\text {d}\zeta . \end{aligned}$$

(20b)

Typical profiles for various $t > 0$ are shown in Fig. 1. Note that

$$\begin{aligned} \lim _{t \rightarrow \infty }P_0(z,t) = \frac{\rho _\mathrm{s} gh}{P_\mathrm{c}} + z \quad \text {for each fixed }\;\; z > 0, \end{aligned}$$

or in terms of the original variables

$$\begin{aligned} \lim _{t \rightarrow \infty }{\widetilde{P}}(z,t) = \rho _\mathrm{s} g (z+h) \quad \text {for each fixed }\;\; z > 0. \end{aligned}$$

(21)

Equation (21) reflects the fact that ponding with a layer of fluid having constant density $\rho _\mathrm{s}$, results in the half-space $\varOmega$ being filled with stagnant fluid of density $\rho _\mathrm{s}$ as $t \rightarrow \infty$.

4 The Perturbation Equations

To investigate the stability of the ground state $\{C_0, \mathbf{U}_0, P_0 \}$ we write the original variables as

$$\begin{aligned} C = C_0 + c, \quad \mathbf{U} = \mathbf{U}_0 + \mathbf{u}, \quad P = P_0 + p, \end{aligned}$$

(22)

where $\mathbf{u} = (u,v,w)^T$. Here c, $\mathbf{u}$ and p are the perturbations whose behavior we need to study. For this, we have to first write the perturbation equations. Substituting (22) in Eq. (14), the initial condition (15a) and the boundary conditions (15b) give

$$\begin{aligned}&\displaystyle \frac{\partial (C_0+c)}{\partial t} = -\nabla \cdot ((C_0+c)(\mathbf{U}_0 + \mathbf{u})) + \varDelta (C_0+c) , \end{aligned}$$

(23a)

$$\begin{aligned}&\displaystyle \frac{1}{\kappa (z)}(\mathbf{U}_0+\mathbf{u}) = -\nabla {(P_0+p)} + (C_0+c)\mathbf{e}_z , \end{aligned}$$

(23b)

$$\begin{aligned}&\displaystyle \nabla \cdot (\mathbf{U}_0+\mathbf{u}) = 0 , \end{aligned}$$

(23c)

subject to

$$\begin{aligned}&C_0 + c = C_i \quad \text {in }\;\; \varOmega ,\;\;\text { for }\;\;t = 0, \end{aligned}$$

(24a)

$$\begin{aligned}&C_0 + c = 1, \quad P_0 + p = 1 \quad \text {at }\;\;z = 0,\;\;\text { for }\;\;t > 0, \end{aligned}$$

(24b)

$$\begin{aligned}&C_0 + c \rightarrow 0, \quad \frac{\partial (P_0 + p)}{\partial z} \rightarrow 0 \quad \text {as }\;\;z \!\rightarrow \! \infty ,\;\;\text { for }\;\;t > 0, \end{aligned}$$

(24c)

and for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ also

$$\begin{aligned}&(\mathbf{U}_0 + \mathbf{u})\cdot \mathbf{n} = 0, \quad (R(\mathbf{U}_0 + \mathbf{u})(C_0 + c) - \nabla (C_0 + c))\cdot \mathbf{n} = 0 \quad \text {along }\;\; \varGamma _v,\;\; \text { for }\;\; t > 0. \end{aligned}$$

(24d)

In view of the properties of the ground-state solution, there results for the perturbations the equations

$$\begin{aligned}&\displaystyle \frac{\partial c}{\partial t} + R\,w\frac{\partial C_0}{\partial z} - \varDelta c + R\,\mathbf{u}\cdot \nabla c= 0, \end{aligned}$$

(25a)

$$\begin{aligned}&\displaystyle \frac{1}{\kappa (z)}\mathbf{u} + \nabla p - c\,\mathbf{e}_z = \mathbf{0} , \end{aligned}$$

(25b)

$$\begin{aligned}&\displaystyle \nabla \cdot \mathbf{u} = 0 , \end{aligned}$$

(25c)

and the boundary conditions

$$\begin{aligned}&c = 0, \quad p = 0\quad \text {at }\;\; z = 0,\;\; \text { for }\;\; t > 0 , \end{aligned}$$

(26a)

$$\begin{aligned}&c \rightarrow 0, \quad \frac{\partial p}{\partial z} \rightarrow 0\quad \text {as }\;\; z \rightarrow \infty \;\; \text {and}\;\; t > 0 , \end{aligned}$$

(26b)

and for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ also

$$\begin{aligned}&\mathbf{u}\cdot \mathbf{n} = 0, \quad \nabla c\cdot \mathbf{n} = 0 \quad \text {along }\;\; \varGamma _v,\;\;\text { for }\;\;t > 0 . \end{aligned}$$

(26c)

Multiplying (25b) by $\kappa (z)$ and applying the divergence gives

$$\begin{aligned} \nabla \cdot \mathbf{u} = 0 = \nabla \cdot (-\kappa (z)\nabla p + \kappa (z)c\mathbf{e}_z). \end{aligned}$$

Hence

$$\begin{aligned} \frac{\partial }{\partial z}\left( -\kappa (z)\frac{\partial p}{\partial z} + \kappa (z)c \right) - \kappa (z)\varDelta _{\perp }p = 0, \end{aligned}$$

where $\varDelta _\perp =\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}$ denotes the horizontal Laplacian. Substituting the vertical component w of the Darcy equation gives

$$\begin{aligned} \frac{\partial w}{\partial z} = \kappa (z)\varDelta _{\perp }p. \end{aligned}$$

(27)

Using this identity, the pressure boundary condition in (26a) implies for w the Neumann condition

$$\begin{aligned} \frac{\partial w}{\partial z} = 0 \quad \text {at }\;\;z = 0,\;\;\text { for }\;\;t > 0. \end{aligned}$$

(28)

Following Lapwood (1948), we take the Laplacian of the vertical component of the perturbation Darcy equation (25b). This gives

$$\begin{aligned} \varDelta \left( \frac{1}{\kappa (z)}w\right) = - \frac{\partial }{\partial z}\varDelta p + \varDelta c. \end{aligned}$$

(29)

Further, taking the divergence of the perturbed Darcy equation (25b) and using (25c),

$$\begin{aligned} \nabla \cdot \left( \frac{1}{\kappa (z)}\mathbf{u}\right) = \mathbf{u} \cdot \nabla \frac{1}{\kappa (z)} = w \frac{\text {d}}{\text {d}z}\frac{1}{\kappa (z)} = -\varDelta p + \frac{\partial c}{\partial z}, \end{aligned}$$

yielding upon differentiation with respect to z

$$\begin{aligned} \frac{\partial }{\partial z}\left( w \frac{\text {d}}{\text {d}z}\frac{1}{\kappa (z)}\right) = -\frac{\partial }{\partial z}\varDelta p + \frac{\partial ^2 c}{\partial z^2}. \end{aligned}$$

(30)

Subtracting (30) from (29) results in

$$\begin{aligned} \varDelta \left( \frac{1}{\kappa (z)}w\right) - \frac{\partial }{\partial z}\left( w \frac{\text {d}}{\text {d}z}\frac{1}{\kappa (z)}\right) = \varDelta _{\perp } c, \end{aligned}$$

or

$$\begin{aligned} \nabla \cdot \left( \frac{1}{\kappa (z)}\nabla w\right) = \varDelta _{\perp } c. \end{aligned}$$

(31)

The Neumann condition (28) and identity (31) will be used frequently in the next sections.

5 Stability Analyses

In the unbounded ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$, we consider x, y-periodic solutions of the perturbation equations with respect to x, y-periodic cells of the form

$$\begin{aligned} \varOmega _A := \{ (x,y,z) : (x,y) \in {\mathcal {T}}, z > 0\}, \end{aligned}$$

(32)

where ${\mathcal {T}} \subset {\mathbb {R}}^2$ is an element (tile) of the horizontal periodic structure. This implies a redefinition of $\varOmega _A$ as introduced in Sect. 2. As noted in Chandrasekhar (1981) or Straughan (2008), ${\mathcal {T}}$ can be a rectangle (or square), a strip or a hexagon. In this paper, the focus is on nonlinear stability and on the onset of infinitesimal small perturbations (linear approach). Details about the characterization of the periodic structure as for instance in Mielke (2002), who studied the spatial structure in the Rayleigh–Bénard problem, are beyond the scope of this paper. Some aspects, though, are discussed in Pieters et al. (2018).

In the linear approach, the horizontal periodicity is described by a function $f = f(x,y)$ that satisfies

$$\begin{aligned} \varDelta _\perp f + a^2 f = 0 \quad \text {in }\;\;{\mathbb {R}}^2 , \end{aligned}$$

(33)

where a is a characteristic wavenumber. If ${\mathcal {T}}$ is a hexagon with side L one has (see Chandrasekhar 1981)

$$\begin{aligned} f(x,y) = \cos \frac{4\pi }{3L}\left( \frac{\sqrt{3}}{2}x + \frac{1}{2}y\right) + \cos \frac{4\pi }{3L}\left( \frac{\sqrt{3}}{2}x - \frac{1}{2}y\right) + \cos \frac{4\pi }{3L}y, \end{aligned}$$

(34a)

and

$$\begin{aligned} a = \frac{4\pi }{3L}. \end{aligned}$$

(34b)

In this paper, we visualize the horizontal periodicity in the form of rectangles ${\mathcal {T}} = (0,\ell _x)\times (0,\ell _y)$, where $\ell _x$ and $\ell _y$ are for the moment unspecified. This yields periodic cells of the form

$$\begin{aligned} \varOmega _A := \{ (x,y,z) : |x|< \ell _x, |y| < \ell _y, z > 0\}. \end{aligned}$$

(35)

In (35), $\ell _x$, $\ell _y$ are dimensionless lengths. A sketch of a two-dimensional cross section of the flow domain in the x, z-plane is shown in Fig. 2.

Fig. 2

Sketch of a two-dimensional cross section of the flow domain in the x, z-plane. In the laterally unbounded ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$: Periodic boundary conditions for the concentration c, the discharge $\mathbf{u}$, and pressure p apply at vertical boundary $\varGamma _v = \varGamma _2 \cup \varGamma _4$. In the laterally bounded ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$: No-flow and no-transport conditions apply at the vertical boundary $\varGamma _v$. For numerical simulations, we consider a truncated column of depth d

In the x, y-periodic assumption, periodic boundary conditions are applied along the vertical boundary of $\varOmega _A$, which we denote by $\varGamma _v$. This means that c, $\mathbf{u}$, and p can be extended in a periodic way over the whole $\varOmega$, and belong to $C^\infty (\varOmega )$.

In the bounded ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, we consider the perturbation equations in the flow domain $\varOmega = \varOmega _B$, which we write as

$$\begin{aligned} \varOmega _B = \{ (x,y,z) : |x|< \pi , |y| < \ell \pi , z > 0\}, \end{aligned}$$

(36)

where $\ell = \frac{L_y}{L_x}$ is a dimensionless length ratio. Here, we use no-flow and no-transport conditions along the vertical boundary $\varGamma _v$.

For computational purposes, see Sect. 6.1.3, we use the depth-truncated versions of $\varOmega _A$ and $\varOmega _B$:

$$\begin{aligned} \varOmega _A^d := \{ (x,y,z) : |x|< \ell _x , |y|< \ell _y, 0< z < d\}, \end{aligned}$$

(37)

and

$$\begin{aligned} \varOmega _B^d := \{ (x,y,z) : |x|< \pi , |y|< \ell \pi , 0< z < d\}. \end{aligned}$$

(38)

where d denotes the dimensionless depth.

In Sect. 5.1, we consider the method of linearized stability, valid for small perturbations, and in Sect. 5.2, the nonlinear, variational energy method.

5.1 Linearized Stability

Assuming the perturbations to be small, one disregards the nonlinear term $\mathbf{u} \cdot \nabla c$ in (25a). The result is the perturbation system

$$\begin{aligned}&\displaystyle \frac{\partial c}{\partial t} + R\,w\frac{\partial C_0}{\partial z} - \varDelta c = 0, \end{aligned}$$

(39a)

$$\begin{aligned}&\displaystyle \nabla \cdot \left( \frac{1}{\kappa (z)} \nabla w\right) = \varDelta _\perp c, \end{aligned}$$

(39b)

$$\begin{aligned}&\displaystyle \frac{\partial w}{\partial z} = \kappa (z)\varDelta _\perp p, \end{aligned}$$

(39c)

in $\varOmega _A$ or $\varOmega _B$, with

$$\begin{aligned}&c = 0, \quad \frac{\partial w}{\partial z} = 0, \quad p = 0 \quad \text {at }\;\; z = 0,\;\; \text { for all }\;\; t > 0 , \end{aligned}$$

(40a)

$$\begin{aligned}&c \rightarrow 0, \quad w \rightarrow 0, \quad \frac{\partial p}{\partial z} \rightarrow 0 \quad \text {as }\;\; z \rightarrow \infty ,\;\; \text { for all }\;\; t > 0 , \end{aligned}$$

(40b)

and with

$$\begin{aligned}&({{{\mathbf {{\small {\uppercase {case~A}}}}}}}) \quad \text {Periodic conditions at }\varGamma _v , \end{aligned}$$

(40c)

$$\begin{aligned}&({{{\mathbf {{\small {\uppercase {case~B}}}}}}}) \quad \text {No-flow and no-transport conditions at }\varGamma _v . \end{aligned}$$

(40d)

Note that (39) is a linear system in terms of c, w (z-component of Darcy velocity), and p. Because of the linearity and the nature of the conditions (40a) and (40b), we may assume that solutions are of the form

$$\begin{aligned} \{c,w,p\}(x,y,z,t) = \{c,w,p\}(z,t)\cos a_x x \cos a_y y, \end{aligned}$$

(41)

Then (40c), (40d) are satisfied provided the wavenumbers satisfy

$$\begin{aligned}&({{{\mathbf {{\small {\uppercase {case~A}}}}}}}) \quad a_x = \frac{n\pi }{\ell _x}, \quad a_y = \frac{m\pi }{\ell _y} \quad n,m=1,2,\ldots \end{aligned}$$

(42a)

$$\begin{aligned}&({{{\mathbf {{\small {\uppercase {case~B}}}}}}}) \quad a_x = n, \quad a_y = \frac{m}{\ell } \quad n,m=1,2,\ldots \end{aligned}$$

(42b)

Substituting (41) in (39) gives for the amplitudes c(z, t), w(z, t), and p(z, t) the equations

$$\begin{aligned}&\displaystyle \frac{\partial c}{\partial t} + R\,w\frac{\partial C_0}{\partial z} = \frac{\partial ^2 c}{\partial z^2} - a^2 c, \end{aligned}$$

(43a)

$$\begin{aligned}&\displaystyle -\frac{\partial }{\partial z}\left( \frac{1}{\kappa (z)} \frac{\partial w}{\partial z}\right) + \frac{a^2}{\kappa (z)} w = a^2 c, \end{aligned}$$

(43b)

$$\begin{aligned}&\displaystyle \frac{\partial w}{\partial z} = -a^2 \kappa (z) p, \end{aligned}$$

(43c)

for $z > 0$ and $t > 0$, subject to conditions (40a), (40b). Here $a^2 = a_x^2 + a_y^2$.

We will study the linearized problem (43) for all $a > 0$ and $R > 0$. However, when interpreting the results in terms of stability we consider

$$\begin{aligned}&({{{\mathbf {{\small {\uppercase {case~A}}}}}}}) \quad a\text { unspecified and }\;\; R \!\equiv \! 1 , \\&({{{\mathbf {{\small {\uppercase {case~B}}}}}}}) \quad a = a_{n,m} = \sqrt{n^2 + (m/\ell )^2}\;\; \text { and }\;\; R = R_S , \end{aligned}$$

where $R_S$ denotes the system Rayleigh number as specified in Table 1.

It suffices to consider Eqs. (43a) and (43b) for c and w only, since p follows directly from equation (43c).

In the following Sects. 5.1.1 and 5.1.2, we use two distinct methods to obtain linear stability results.

5.1.1 Direct $L^2$-estimate

To obtain an estimate for the $L^2$-norm of the concentration perturbation, we multiply equation (43a) by c and integrate the result in z. This gives the expression

$$\begin{aligned}&\frac{1}{2}\frac{\text {d}}{\text {d}t}\int _0^\infty c^2(z,t)~\text {d}z + \int _0^\infty \left( \frac{\partial c}{\partial z}(z,t) \right) ^2~\text {d}z \nonumber \\&\quad =-a^2\int _0^\infty c^2(z,t)~\text {d}z - R\int _0^\infty c(z,t) w(z,t)\frac{\partial C_0}{\partial z}(z,t)~\text {d}z \end{aligned}$$

(44)

for each $t > 0$.

Since the ground-state saturation $C_0$ satisfies

$$\begin{aligned} 0 < -\frac{\partial C_0}{\partial z}(z,t) \leqslant -\frac{\partial C_0}{\partial z}(0,t) = \frac{1}{\sqrt{\pi t}} \quad \text {for}\;\; z> 0\;\; \text {and}\;\; t > 0 , \end{aligned}$$

(45)

we can estimate (44) by, disregarding the second term in the left side as well,

$$\begin{aligned} \frac{1}{2}\frac{\text {d}}{\text {d}t}\int _0^\infty c^2(z,t)~\text {d}z \leqslant -a^2\int _0^\infty c^2(z,t)~\text {d}z + \frac{R}{\sqrt{\pi t}}\int _0^\infty |c(z,t) w(z,t)|~\text {d}z \end{aligned}$$

for $t > 0$.

Introducing the $L^2$-norm (i.e., $||c||_2^2 = \int _0^\infty c^2~\text {d}z$) and dropping t from the notation, this inequality is written in the compact form

$$\begin{aligned} \frac{1}{2}\frac{\text {d}}{\text {d}t}||c||_2^2 \leqslant -a^2||c||_2^2 + \frac{R}{\sqrt{\pi t}}\int _0^\infty |c w|~\text {d}z\; . \end{aligned}$$

(46)

At this point, we use the Cauchy–Schwarz inequality

$$\begin{aligned} \int _0^\infty |cw|~\text {d}z \leqslant ||c||_2 ||w||_2, \end{aligned}$$

to estimate (46) further as

$$\begin{aligned} \frac{1}{2}\frac{\text {d}}{\text {d}t}||c||_2^2 \leqslant -a^2||c||_2^2 + \frac{R}{\sqrt{\pi t}}||c||_2||w||_2. \end{aligned}$$

(47)

Next, we multiply (43b) by w and integrate the result. Using the Neumann condition (28), this yields

$$\begin{aligned} \int _0^\infty \frac{1}{\kappa (z)}\left( \frac{\partial w}{\partial z}\right) ^2~\text {d}z + a^2\int _0^\infty \frac{1}{\kappa (z)}w^2~\text {d}z = a^2\int _0^\infty w c~\text {d}z. \end{aligned}$$

(48)

Now let ${\overline{\kappa }} = \max _{z \geqslant 0} \kappa (z)$. Then, we deduce from (48)

$$\begin{aligned} \frac{1}{{\overline{\kappa }}}||w||_2^2&\leqslant \int _0^\infty |w| |c|~\text {d}z \\&\leqslant ||w||_2 ||c||_2, \end{aligned}$$

where we used again Cauchy–Schwarz. Thus

$$\begin{aligned} ||w(t)||_2 \leqslant {\overline{\kappa }}||c(t)||_2 \quad \text {for }\;\; t > 0 . \end{aligned}$$

(49)

Applying this inequality in (47) gives

$$\begin{aligned} \frac{\text {d}}{\text {d}t}||c||_2^2 \leqslant \left( -2a^2 + \frac{2R{\overline{\kappa }}}{\sqrt{\pi t}}\right) ||c||_2^2. \end{aligned}$$

(50)

Integrating this expression in t yields the estimate

$$\begin{aligned} ||c(t)||_2 \leqslant ||c(0)||_2 \hbox {e}^{-a^2 t + \frac{2R{\overline{\kappa }}}{\sqrt{\pi }}\sqrt{t}}. \end{aligned}$$

(51)

By (49), the same holds for $||w(t)||_2$. Next, we apply (49) in (48) to find

$$\begin{aligned} \int _0^\infty \frac{1}{\kappa (z)}\left( \frac{\partial w}{\partial z}\right) ^2~\text {d}z \leqslant a^2\int _0^\infty |w c|~\text {d}z \leqslant a^2 ||w||_2 ||c||_2 \leqslant a^2 {\overline{\kappa }}||c||_2^2. \end{aligned}$$

Using this inequality and (43c), we obtain

$$\begin{aligned} \int _0^\infty \kappa (z) p^2~\text {d}z = \frac{1}{a^4}\int _0^\infty \frac{1}{\kappa (z)}\left( \frac{\partial w}{\partial z}\right) ^2~\text {d}z \leqslant \frac{{\overline{\kappa }}}{a^2}||c||_2^2. \end{aligned}$$

Hence

$$\begin{aligned} ||p(t)||_2 \leqslant \frac{1}{a}\sqrt{\frac{{\overline{\kappa }}}{{\underline{\kappa }}}}||c(t)||_2 \qquad \text {for }t > 0 , \end{aligned}$$

(52)

where ${\underline{\kappa }} = \min _{z \geqslant 0}\kappa (z)$.

Thus both the pressure p and the vertical flow w decay like c. Estimate (51) says that x, y-periodic perturbations, characterized by the wave number a, eventually decay in time if the initial amplitude $c(0) \in L^2([0,\infty ))$ (i.e., $\int _0^\infty c(0)^2~\text {d}z < \infty$). This is due to the term $-a^2t$ in the exponent. In essence, this is a diffusive term. This can be seen when going back to the dimensional form

$$\begin{aligned} a^2 t \longrightarrow {\left\{ \begin{array}{ll} \left( a \frac{D}{Q_\mathrm{c}}\right) ^2\frac{Q_\mathrm{c}^2 t}{\phi D}, &{}\quad ({{{\mathbf {{\small {\uppercase {case~A}}}}}}}) \\ \left( a L_\mathrm{c}\right) ^2\frac{Dt}{\phi L_\mathrm{c}^2},&{}\quad ({{{\mathbf {{\small {\uppercase {case~B}}}}}}}) \end{array}\right. } \end{aligned}$$

where now a and t are dimensional. A sketch of the upperbound in (51) is shown in Fig. 3. Note that the maximum is reached at

$$\begin{aligned} t = T_d = \frac{R^2{\overline{\kappa }}^2}{a^4\pi }. \end{aligned}$$

Fig. 3

Stability upperbound by direct $L^2$-estimate: right-hand side in (51)

The stability result expressed by (51) was derived using the rather crude estimate (45). In the next section, we do not use (45). Instead, we consider the growth or decay of small perturbations of $C_0(z,t)$ for each $t > 0$.

For future reference, we introduce

$$\begin{aligned} R_M = R_M(a,t) := \frac{a^2\sqrt{\pi t}}{{\overline{\kappa }}}. \end{aligned}$$

(53)

Using this in (50) gives the form

$$\begin{aligned} \frac{\text {d}}{\text {d}t}||c||_2^2 \leqslant -2a^2 \left\{ 1 - \frac{R}{R_M} \right\} ||c||_2^2, \end{aligned}$$

(54)

implying that if $R < R_M(a,t)$, then $L^2$-stability of the linearized system is guaranteed.

5.1.2 Eigenvalue Formulation

Again we start from the linear system (43). In case of a steady, i.e., time independent, ground state, as in Wooding et al. (1997a, b), one looks for amplitudes c and w that have an exponential growth rate in time, i.e., $\{c,w\}(z,t) = \{c,w\}(z)\hbox {e}^{\sigma t}$. If $\sigma < 0$, then all small perturbations decay in time and we call the system linearly asymptotic stable. If, on the other hand, $\sigma > 0$, then small perturbations grow exponentially in time and we call the system unstable.

In this paper, the ground state depends on time as well. However, since $\frac{\partial C_0}{\partial z}(z,t+\tau ) \!\approx \! \frac{\partial C_0}{\partial z}(z,t)$ for $|\tau |$ being sufficiently small, we proceed similarly as in the steady case. This is called the ’frozen-profile’ approach (van Duijn et al. 2002).

Hence, for given $t > 0$, we consider instead of (43a) the approximate equation

$$\begin{aligned} \frac{\partial c}{\partial \tau } + R\,w\frac{\partial C_0}{\partial z}(z,t) = \frac{\partial ^2 c}{\partial z^2} - a^2 c, \end{aligned}$$

(55)

for $\tau > 0$, but sufficiently small. Now time t appears as a parameter in the equation. We then assume that the perturbations have an exponential growth rate denoted by $\sigma$, i.e.,

$$\begin{aligned} \{c,w\}(z,\tau ) = \{c,w\}(z)\exp (\sigma \tau ). \end{aligned}$$

(56)

Substituting (56) into (55) and (43b) yields the following eigenvalue problem: For given $a > 0$, $t > 0$ and $\sigma$, find the smallest $R > 0$ (denoted by $R = R_1(a,t,\sigma )$) so that the problem

$$\begin{aligned} \sigma c = \frac{\text {d}^2 c}{\text {d}z^2} - a^2 c - R\,w\frac{\partial C_0}{\partial z}(z,t), \end{aligned}$$

(57a)

$$\begin{aligned} -\frac{\text {d}}{\text {d}z}\left( \frac{1}{\kappa (z)}\frac{\text {d}w}{\text {d}z}\right) + \frac{a^2}{\kappa (z)}w = a^2\,c, \end{aligned}$$

(57b)

for $z > 0$, with

$$\begin{aligned}&c = 0, \quad \frac{\text {d}w}{\text {d}z} = 0 \quad \text {at }\;\;z = 0 , \end{aligned}$$

(57c)

$$\begin{aligned}&c \rightarrow 0, \quad w \rightarrow 0\quad \text {as }\;\;z \!\rightarrow \! \infty \end{aligned}$$

(57d)

has a nontrivial solution.

The eigenvalues now depend on a, t, and on the growth rate $\sigma$. In the salt lake problem (Pieters and van Duijn 2006), it was shown that the smallest positive eigenvalue $R_1(a,t,\sigma )$ satisfies

$$\begin{aligned} R_1(a,t,\sigma ) \lessgtr R_1(a,t,0) \quad \text {if and only if }\;\; \sigma \lessgtr 0 . \end{aligned}$$

(58)

This expresses exchange of stability. We assume here that (58) also holds for the eigenvalue problem (57). Under this assumption, which is supported by numerical evidence in Pieters et al. (2018), it suffices to analyze (57) for the case of neutral stability, i.e., $\sigma \!\equiv \! 0$.

For completeness, we write the eigenvalue problem resulting from linearized stability.

Note that here $a > 0$ and $t > 0$ act as parameters. The smallest positive eigenvalue is denoted by $R_L = R_L(a,t)$. We return to this problem in Sect. 6.1.1.

The behavior of large perturbations is studied in the next section.

5.2 The Variational Energy Method

The method of linearized stability holds for infinitesimal small perturbations. What can be said about the system behavior for larger perturbations. To address this point, we apply the variational energy approach, see van Duijn et al. (2002) for the specific application to the salt lake problem and Straughan (1992, 2008) for a general overview.

Remark 4

The energy method can be applied for both domain $\varOmega _A$ (${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$) and $\varOmega _B$ (${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$). In the derivation that follows, we use $\varOmega _{i}$ to denote the flow domain. The index i can refer to A or B. Both geometrical cases would give the same equations, although the interpretation of the stability results is different.

In the energy method, one estimates the time derivative of the $L^2$-norm of the concentration perturbation c. In particular, the aim is to find the largest R-interval for which

$$\begin{aligned} \frac{\text {d}}{\text {d}t}\int _{\varOmega _{i}}c^2 < 0 \quad \text {for all }\;\; t > 0 . \end{aligned}$$

(60)

Here and in the integrals below, we disregard the infinitesimal volume elements in the notation. The related maximum R-value clearly will depend on the wavenumber a and, because $C_0 \!=\! C_0(z,t)$, on time t. Starting point here is the nonlinear system (25).

To investigate (60), we multiply (25a) by c and integrate over $\varOmega _{i}$. Using (25c) and the boundary conditions along $\varGamma _v$, we find the identity:

$$\begin{aligned} \frac{1}{2}\frac{\text {d}}{\text {d}t}\int _{\varOmega _{i}}c^2 = -\int _{\varOmega _{i}}|\nabla c|^2 - R\int _{\varOmega _{i}}cw\frac{\partial C_0}{\partial z}. \end{aligned}$$

(61)

Thus, if R is chosen such that the right-hand side of (61) is negative for all perturbations satisfying a given constraint which is closest to the solution of the problem, then stability is guaranteed.

Roughly, there exist two approaches to incorporate the constraint on the admissible perturbations. One is based on (25c) (see Homsy and Sherwood 1976), and the integrated Darcy equation (25b):

$$\begin{aligned} \nabla \cdot \mathbf{u} = 0 , \quad \int _{\varOmega _{i}}\frac{1}{\kappa (z)}|\mathbf{u}|^2 - \int _{\varOmega _{i}}cw = 0. \end{aligned}$$

(62)

The other approach, and the one we focus on in this paper, uses the point-wise differential expression (31) as constraint:

$$\begin{aligned} \nabla \cdot \left( \frac{1}{\kappa (z)}\nabla w\right) = \varDelta _{\perp }c \quad \text {in}\;\; \varOmega _i . \end{aligned}$$

Applied to the salt lake problem, van Duijn et al. (2002) showed that this gives sharper results than constraint (62). It leads to the following class of admissible perturbations:

$$\begin{aligned} {\mathscr {H}}= & {} \Biggl \{(c,w) \ne (0,0) : c, w\text { (or }\mathbf{u}\text {) are }x,y\text {-periodic with respect to }\varOmega _{i} , \\ c= & {} \frac{\partial w}{\partial z} = 0\text { at }z\!=\!0, c = w \!=\! 0\text { as }z \!\rightarrow \! \infty ,\text { and }\nabla \cdot \left( \frac{1}{\kappa (z)}\nabla w \right) = \varDelta _{\perp }c\text { in } \varOmega _i \Biggr \}. \end{aligned}$$

In the energy method, the goal is to determine the largest R-interval for which

$$\begin{aligned} \int _{\varOmega _{i}}|\nabla c|^2 + R\int _{\varOmega _{i}} cw \frac{\partial C_0}{\partial z} > 0 \quad \text {for all }\;\;(c,w) \in {\mathscr {H}}. \end{aligned}$$

To this end, we consider the maximum problem

$$\begin{aligned} \frac{1}{R_E} = \sup _{(c,w) \in {\mathscr {H}}} \frac{-\int _{\varOmega _{i}} cw \frac{\partial C_0}{\partial z}}{\int _{\varOmega _{i}}|\nabla c|^2}. \end{aligned}$$

(63)

The boundedness of the functional in this expression is a direct consequence of the choice of space ${\mathscr {H}}$ and the behavior of $\frac{\partial C_0}{\partial z}$. This is detailed in Pieters et al. (2018), “Appendix E”.

Suppose this maximum problem has a solution (i.e., there exists such a $R_E \in (0,\infty )$). Then any solution of (25), (26), and (28) satisfies

$$\begin{aligned} \frac{1}{R_E} \geqslant \frac{-\int _{\varOmega _{i}} cw \frac{\partial C_0}{\partial z}}{\int _{\varOmega _{i}}|\nabla c|^2}, \end{aligned}$$

and thus for any $R < R_E$ one obtains from (61)

$$\begin{aligned} \frac{1}{2}\frac{\text {d}}{\text {d}t}\int _{\varOmega _{i}}c^2 \leqslant -\left( 1 - \frac{R}{R_E}\right) \int _{\varOmega _{i}} |\nabla c|^2 < 0. \end{aligned}$$

Hence, for $R < R_E$, the system is unconditionally stable.

Maximum problem (63) is equivalent to the following minimum problem: Find the smallest $R_E > 0$ so that

$$\begin{aligned} \inf _{(c,w) \in {\mathscr {H}}} \left\{ \int _{\varOmega _{i}}|\nabla c|^2 + R_E\int _{\varOmega _{i}}cw\frac{\partial C_0}{\partial z} \right\} = 0. \end{aligned}$$

(64)

To solve (64), we introduce the functional

$$\begin{aligned} J(c,w,\pi ; R) = \int _{\varOmega _{i}}|\nabla c|^2 + R\int _{\varOmega _{i}}cw\frac{\partial C_0}{\partial z} + \int _{\varOmega _{i}}\pi \left[ \nabla \cdot \left( \frac{1}{\kappa (z)}\nabla w\right) - \varDelta _{\perp }c \right] , \end{aligned}$$

(65)

where $\pi$ acts as a Lagrange multiplier. We need to find points $(c,w,\pi )$, with $(c,w) \!\in \! {\mathscr {H}}$ and $\pi$ is $\varOmega _{i}$-periodic, $\lim _{z \rightarrow \infty } \pi (z) = 0$, and values of R where the first variation of (65) vanishes. This leads to the Euler–Lagrange equations

$$\begin{aligned} -2\varDelta c + R\frac{\partial C_0}{\partial z}w&= \varDelta _{\perp }\pi , \end{aligned}$$

(66a)

$$\begin{aligned} \nabla \cdot \left( \frac{1}{\kappa (z)}\nabla \pi \right)&= -R\frac{\partial C_0}{\partial z}c , \end{aligned}$$

(66b)

$$\begin{aligned} \nabla \cdot \left( \frac{1}{\kappa (z)}\nabla w\right)&= \varDelta _{\perp }c, \end{aligned}$$

(66c)

in $\varOmega _{i}$. Moreover, $\frac{\partial \pi }{\partial z}(0) = 0$ appears as a natural boundary condition. Details of the derivation are given in Pieters et al. (2018).

Thus far $\varOmega _{i}$ has been left general. Explicitly considering periodicity of the form (41) for c, $\pi$, and w, which is allowed since the equations in (66) are linear, yields the eigenvalue problem

Here, the smallest positive eigenvalue is denoted by $R_E \!=\! R_E(a,t)$. We return to this problem in Sect. 6.

6 Stability Results

6.1 Homogeneous Soils

When considering homogeneous soils, we set $\kappa (z) = 1$ in problems $(P_L)$ and $(P_E)$. We show below that this makes it possible to eliminate the time t from the eigenvalue problems. As a consequence, we obtain a clear interpretation of the role of a, $R_S$ and t in the stability behavior.

6.1.1 Eigenvalue Approach

The interpretation of the eigenvalues in terms of the wave number a and time t is not straightforward. Taking t as parameter, the eigenvalues $R_L(\cdot , t)$ and $R_E(\cdot ,t)$ as function of $a > 0$, do not show a clear ordering. However, since

$$\begin{aligned} \frac{\partial C_0(z,t)}{\partial z} = -\frac{1}{\sqrt{\pi t}}\hbox {e}^{-\frac{z^2}{4t}}, \end{aligned}$$

we can remove t from ($P_L$) and ($P_E$) by introducing the variables

$$\begin{aligned} \eta := \frac{z}{\sqrt{t}}, \quad \{c,w,\pi \}(\eta ) := \{c,w,\pi \}(z,t), \quad b := a\sqrt{t}, \quad \text {and}\quad R^* := \sqrt{\frac{t}{\pi }}R. \end{aligned}$$

(68)

Applying (68) to ($P_L$) and ($P_E$) yields transformed eigenvalue problems in terms of the same similarity variable as the ground state. The resulting problems read

and

Clearly, now $R_L^*$ and $R_E^*$ depend on b only. This allows for a more transparent interpretation of the stability results.

To find the smallest possible eigenvalues for $b > 0$, we solve $(P_L^*)$ and $(P_E^*)$ by means of a Chebyshev–Petrov–Galerkin spectral method. Details and references are given in Pieters et al. (2018). The result is shown in Fig. 4. Note that $R_L^*(b) > R_E^*(b)$ for all $b > 0$, but the difference is small for $b > 0.5$. This is different from the salt lake problem (van Duijn et al. 2002), where there is a significant gap between $R_L$ and $R_E$. In this gap, small perturbations vanish, but large perturbations may grow in time. Since for all practical purposes, see Fig. 4,

$$\begin{aligned} R_L^*(b) \approx R_E^*(b) \quad \text {for}\;\;b > 0,\text { say}, \end{aligned}$$

(71)

the ponded problem considered in this paper has a sharp stability bound: below $R_E^*$ there is unconditional stability and above $R_L^*$ instability.

Remark 5

For ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$, there is no defined system Rayleigh number $R_S$. However, one still has the Rayleigh number $R^*$ showing up in the eigenvalue problems due to the similarity transformation. This system Rayleigh number then refers to time only, as $R^* \!=\! \sqrt{\frac{t}{\pi }}$.

Fig. 4

Stability curves for the ponded case, according to the direct approach $R^*_M$, method of linearized stability $R^*_L$ and energy method with differential constraint $R^*_E$

Remark 6

Using Green’s functions, one can write w and $\pi$ in $(P_L^*)$ and $(P_E^*)$ in terms of c. Substituting this into ((69a) and ((70a)), and applying again the Green’s function, yields eigenvalue problems in terms of integral equations for c. These transformations and some mathematical properties of the integral forms are detailed in Pieters et al. (2018). In particular, since $c(0) = \frac{\text {d}w}{\text {d}\eta }(0) = \frac{\text {d}\pi }{\text {d}\eta }(0) = 0$, the corresponding integral equations are nonselfadjoint.

We show in Pieters et al. (2018) that both $R_L^*(b)$ and $R_E^*(b)$ have the lower bound:

$$\begin{aligned} R_L^*(b), R_E^*(b)> b^2 \quad \text {for all }\;\;b > 0 . \end{aligned}$$

This estimate is obtained by manipulating the equations in $(P_L^*)$ and $(P_E^*)$. Recalling that, see (53) with ${\overline{\kappa }} = 1$, $R_M = R_M(a,t) \!=\! a^2\sqrt{\pi t}$, we find after applying (68),

$$\begin{aligned} R_M^*(b) = \sqrt{\frac{t}{\pi }}R_M = b^2. \end{aligned}$$

Hence, the stability bound obtained by the direct $L^2$-estimate of the linearized equations is a lower bound for both $R_L^*(b)$ and $R_E^*(b)$.

Fig. 5

Repetition of Fig. 4, but now it includes dashed lines $R_S^*(b) = \frac{R_S}{a\sqrt{\pi }} b$ for three different pairs $(a,R_S)$: (a) case where $R^*(b)$ lies below $R_E^*(b)$ - system unconditional stable for chosen $(a,R_S)$ value; (b) border case where $R^*(b)$ touches $R_E^*(b)$ at $b = b^*$; (c) case where $R^*(b)$ intersects $R_L^*(b)$ in $b_L^*$ and $b_R^*$

6.1.2 Stability Interpretation

How to interpret and estimate the (in)stability from Fig. 4? For simplicity, we assume that (71) holds. The fact that $R_L^*(b) > R_E^*(b)$ close to $b = 0$ requires only a minor modification of the argument. Let $a > 0$ be a given wavenumber and let $R_S$ be the system Rayleigh number. In view of (68), we have

$$\begin{aligned} \begin{aligned} {{{\mathbf {{\small {\uppercase {case~A}}}}}}}\quad R_S^*&= \sqrt{\frac{t}{\pi }} = \frac{b}{a\sqrt{\pi }} =: R_S^*(b). \\ {{{\mathbf {{\small {\uppercase {case~B}}}}}}}\quad R_S^*&= \sqrt{\frac{t}{\pi }}R_S = \frac{R_S}{a\sqrt{\pi }}b =: R_S^*(b). \end{aligned} \end{aligned}$$

(72)

Hence, $R_S^*(b)$ is a straight line passing through the origin in the $(b,R^*)$-plane. With reference to Fig. 5, three cases can be distinguished, depending on whether the straight line lies (a) entirely below $R_E^*$, or (b) touches $R_E^*$ at $b^*$, or (c) intersects $R_E^*$ at $b_L^*$ and $b_R^*$. We successively consider cases (b), (a), and (c).

Let $\alpha > 0$ be such that the line $\alpha b$ is below $R_E^*(b)$, except at $b = b^*$ where it touches $R_E^*$:

$$\begin{aligned} \alpha b^* = R_E^*(b^*) \quad \text {and} \quad \alpha b < R_E^*(b) \quad \text {for }\;\;b \!\ne \! b^* . \end{aligned}$$

(73)

Numerically, we found

$$\begin{aligned} \alpha = \alpha _{\mathrm{crit}} \approx \frac{6.82}{\sqrt{\pi }} \approx 3.85 \quad \text {and} \quad b = b^* \approx 1.01 . \end{aligned}$$

Writing $R^*(b) = \alpha b$, we have for $\alpha < \alpha _{\mathrm{crit}}$

$$\begin{aligned} R^*(b) < R_E^*(b) \quad \text {for all }\;\; b > 0 . \end{aligned}$$

Thus if

$$\begin{aligned} {{{\mathbf {{\small {\uppercase {case~A}}}}}}}\quad \frac{1}{a\sqrt{\pi }}&< \alpha _{\mathrm{crit}} \;\;\text {or}\;\; a> \frac{1}{6.82}, \\ {{{\mathbf {{\small {\uppercase {case~B}}}}}}}\quad \frac{R_S}{a\sqrt{\pi }}&< \alpha _{\mathrm{crit}} \;\;\text {or}\;\; a > \frac{R_S}{6.82}, \end{aligned}$$

then the ground state is unconditional stable.

How to interpret the result?

${{{\mathbf {{\small {\uppercase {case~A}}}}}}}:$ When considering a specific horizontal structure, for certain $\ell _x$ and $\ell _y$, the wavenumber a has the discrete values

$$\begin{aligned} a_{n,m} = \sqrt{\left( \frac{n\pi }{\ell _x}\right) ^2 + \left( \frac{m\pi }{\ell _y}\right) ^2} \quad n,m = 1,2,\ldots . \end{aligned}$$

Thus if the smallest value $a_{1,1}$ satisfies

$$\begin{aligned} a_{1,1} = \sqrt{\left( \frac{\pi }{\ell _x}\right) ^2 + \left( \frac{\pi }{\ell _y}\right) ^2} \geqslant \frac{1}{6.82}, \end{aligned}$$

(74)

then the ground state is $L^2$-stable for perturbations that are x, y-periodic with respect to a rectangular structure with $\ell _x$ and $\ell _y$ satisfying (74). But perturbations with larger wavelengths (or smaller wavenumbers) may grow in time to form finger-like patterns.

${{{\mathbf {{\small {\uppercase {case~B}}}}}}}:$ Then a takes the discrete values

$$\begin{aligned} a_{n,m} = \sqrt{n^2 + \left( \frac{m}{\ell }\right) ^2} \qquad n,m = 1,2,\ldots . \end{aligned}$$

If the horizontal dimensions of the vertical column $\varOmega _B$ satisfy

$$\begin{aligned} a_{1,1} = \sqrt{1 + \left( \frac{1}{\ell }\right) ^2} \geqslant \frac{R_S}{6.82}, \end{aligned}$$

(75)

then the ground state is $L^2$-stable in $\varOmega _B$ implying that no fingers can occur as a result of initial perturbations.

If $\alpha > \alpha _{\mathrm{crit}}$, then $R_S^*(b)$ intersects $R_L^*(b) \approx R_E^*(b)$ at the points $b_L^*$ and $b_R^*$ as indicated in Fig. 5:

$$\begin{aligned} R_S^*(b) > R_E^*(b) \quad \text {for }b_L^*< b< b_R^* \quad \text {and} \quad R_S^*(b) < R_E^*(b) \quad \text {elsewhere}. \end{aligned}$$

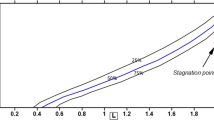
Clearly, the intersection points $b_L^*$ and $b_R^*$ depend on a and $R_S$: $b^*_i = b^*_i(a, R_S)$ for $i = L, R$. For a given system, Rayleigh number $R_S$, the boundary curves in the (a, t)-plane corresponding to $a\sqrt{t} = b_i^*(a,R_S)$ ($i \!=\! L,R$) are shown in Fig. 6 (Left: ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$, Right: ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$). These curves meet when $\frac{R_S}{a} = 6.82$, since then $b_L^* = b_R^* = b^*$.

Above the composite curve (red and blue curves in Fig. 5), one has $L^2$-stability and below the curve small perturbations grow in time. Let $a \!=\! a_{1,1}$, see (74) or (75), denote again the smallest wavenumber for a given $\varOmega _A$ or $\varOmega _B$: i.e., the most unstable mode for a given geometry. Then, with reference to Fig. 6, perturbations decay in time when $0< t < t_L(a)$, they grow when $t_L(a)< t < t_R(a)$, and finally again decay when $t > t_R(a)$. Here $t_i(a) \!=\! (b^*_i/a)^2$ with $i = L,R$.

In Sect. 7, we return to Figs. 5 and 6 for the interpretation in terms of the physical parameters.

Fig. 6

Regions of (in)stability in (t, a)-plane. The blue curves correspond to $t = (b^*_R / a)^2$, and the red curves to $t = (b^*_L / a)^2$. a${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$. b${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ for $R_S \!=\! 20$, $R_S = 15$, and $R_S = 6.82$. For the maxima, it holds that $a = b^*/\sqrt{t}$. For $t < t_L(a)$ and $t > t_R(a)$ the system is stable (indicated by s), while for $t_L(a)< t < t_R(a)$ the system has an episode of transient instability (indicated by u): perturbations having wave number a will first decay, then grow and eventually decay again in time

6.1.3 Direct Numerical Simulations

To verify and interpret our theoretical findings we make a comparison with the nonlinear dynamics described by the full set of Eq. (14). To this end, we perform direct numerical simulations of (14) in two-dimensional cells:

$$\begin{aligned} {{{\mathbf {{\small {\uppercase {case~A}}}}}}}\quad&{\widehat{\varOmega }}_{A}^d := \varOmega _{A}^d \,\,\cap \{y = 0\}; \\ {{{\mathbf {{\small {\uppercase {case~B}}}}}}}\quad&{\widehat{\varOmega }}_{B}^d := \varOmega _{B}^d \,\,\cap \{y = 0\}, \end{aligned}$$

see also Fig. 2.

Having a two-dimensional flow domain in which $\nabla \cdot \mathbf{U} = 0$, allows us to formulate the convective flow part in (14) in terms of the stream function $\varPsi$; i.e.,

$$\begin{aligned} \mathbf{U} = (q_x, q_z) \quad \text {where} \quad q_x = -\frac{\partial \varPsi }{\partial z}, \quad q_z = \frac{\partial \varPsi }{\partial x}. \end{aligned}$$

(76)

Taking the two-dimensional curl of the Darcy equation (14b) and substituting (76) into the result gives for $\varPsi$ the equation (de Josselin de Jong 1960; Bear 1972)

$$\begin{aligned} \nabla \cdot \left( \frac{1}{\kappa (z)} \nabla \varPsi \right) = \frac{\partial C}{\partial x}. \end{aligned}$$

(77)

In the computations presented in this Section, we use $\kappa (z) = 1$, since the soil is considered homogeneous. Later, in Sect. 6.2, we allow $\kappa = \kappa (z)$.

The salt transport equation in terms of $\varPsi$ becomes

$$\begin{aligned} \frac{\partial C}{\partial t} + R\left( \frac{\partial \varPsi }{\partial x}\frac{\partial C}{\partial z} - \frac{\partial \varPsi }{\partial z}\frac{\partial C}{\partial x}\right)&= \varDelta C. \end{aligned}$$

(78)

At the top $\varGamma _3$, we have $P = 1$. This means that $q_x = -\frac{\partial P}{\partial x} = 0$ at $\varGamma _3$. Hence, from (76)

$$\begin{aligned} C = 1 \quad \text {and} \quad \frac{\partial \varPsi }{\partial z} = 0 \quad \text {at }\;\;\varGamma _3 . \end{aligned}$$

(79)

At the bottom $\varGamma _1$, we prescribe $C = 0$ and $\frac{\partial P}{\partial z} = 0$, see (14c). This means that $\frac{1}{\kappa (d)}q_z = 0$ at $\varGamma _1$. Hence, again from (76),

$$\begin{aligned} C = 0 \quad \text {and} \quad \varPsi = \text {constant} = 0 \quad \text {at }\;\;\varGamma _1 . \end{aligned}$$

(80)

For ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$, we impose periodic boundary conditions on C and $\varPsi$ along the vertical boundary $\varGamma _v$. This means that for all $t > 0$

$$\begin{aligned} \left. C\right| _{\varGamma _2} = \left. C\right| _{\varGamma _4}, \quad \left. \frac{\partial C}{\partial x}\right| _{\varGamma _2} = \left. \frac{\partial C}{\partial x}\right| _{\varGamma _4}, \end{aligned}$$

(81)

and

$$\begin{aligned} \left. \varPsi \right| _{\varGamma _2} = \left. \varPsi \right| _{\varGamma _4}, \quad \left. \frac{\partial \varPsi }{\partial x}\right| _{\varGamma _2} = \left. \frac{\partial \varPsi }{\partial x}\right| _{\varGamma _4}. \end{aligned}$$

(82)

For ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, we impose no-flow and no-transport conditions along $\varGamma _v$, i.e., for $t > 0$

$$\begin{aligned} \left. \frac{\partial C}{\partial x}\right| _{\varGamma _2} = \left. \frac{\partial C}{\partial x}\right| _{\varGamma _4} = 0, \end{aligned}$$

(83)

and

$$\begin{aligned} \left. \frac{\partial \varPsi }{\partial z}\right| _{\varGamma _2} = \left. \frac{\partial \varPsi }{\partial z}\right| _{\varGamma _4} = 0. \end{aligned}$$

(84)

We prescribe an initial concentration

$$\begin{aligned} C(x,z,0) = C_i(x,z) \end{aligned}$$

(85)

in ${\widehat{\varOmega }}_{A}^d$ for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ or ${\widehat{\varOmega }}_{B}^d$ for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$. Equations (77) and (78) and conditions (79)–(85) define the problem (NSP), the numerical solution problem. This problem has a unique solution $\{C,\varPsi \}$ for any reasonable initial concentration (85), e.g., see Clément et al. (1992).

Remark 7

Repeating ${\widehat{\varOmega }}_{A}^d$ in horizontal direction yields a smooth $2\ell _x$-periodic solution in the strip $\varOmega ^d \!:=\! \{0< z < d\}$. If the initial concentration $C_i$ is symmetric with respect to $x = 0$, then the same holds for the evolving concentration C and anti-symmetry holds for the corresponding stream function $\varPsi$: i.e.,

$$\begin{aligned} \left. \begin{array}{l l} C(x,z,t) = C(-x,z,t), \\ \varPsi (x,z,t) \!=\! -\varPsi (-x,z,t) \end{array} \right\} \quad \text {for }\;\; (x,z) \in {\widehat{\varOmega }}_{A}^d\;\; \text {and}\;\;t > 0 . \end{aligned}$$

In view of the periodic boundary conditions, this implies

$$\begin{aligned} \left. \frac{\partial C}{\partial x}\right| _{\varGamma _2} = \left. \frac{\partial C}{\partial x}\right| _{\varGamma _4} = 0 \end{aligned}$$

and

$$\begin{aligned} \left. \varPsi \right| _{\varGamma _2} = \left. \varPsi \right| _{\varGamma _4} = 0 \end{aligned}$$

for all $t > 0$. Thus for symmetric initial data, there is no transport across the vertical boundaries. Clearly, this does not hold for arbitrary initial data.

Problem (NSP) is solved by means of a characteristic–Galerkin finite element method. In the method, the convective operator is split from the diffusive one and is written in the form of the material derivative. A detailed description of this method is given in Pieters et al. (2018).

Let the flow domain ${\widehat{\varOmega }}_{i}^d$, with $i = A, B$, be discretized by a set of elements, forming a mesh ${\mathcal {M}}$. The element size of the mesh ${\mathcal {M}}$ will be denoted by $\varDelta {\mathcal {M}}$. Further, time is discretized by the time-grid $t^n \!:=\! n\varDelta t$, $n = 1,2,\ldots ,N$. We denote the numerical solution of problem (NSP) by $\{{\widetilde{C}}_m^n, {\widetilde{\varPsi }}_m^n\}$, where m indexes over the elements in ${\mathcal {M}}$, and n indexes over a discrete time grid.

To quantify the temporal behavior of the full system subject to an initial perturbation, we consider as a stability measure the discrete $L^2$-norm in $\varOmega _i$:

$$\begin{aligned} E(t^n) := \sqrt{\sum _{m \in {\mathcal {M}}}w_m \left[ {\widetilde{C}}_m^n - {\widetilde{C}}_{0,m}^n\right] ^2}. \end{aligned}$$

In this definition, we do not use the analytical ground state $C_0$ evaluated per element and time-grid point, but rather its numerical approximation ${\widetilde{C}}_{0,m}^n$.

We discuss (direct) numerical simulations for both ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$. For ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$, an overview of the stability results is shown in Table 2. There we present for different wavenumbers a stability overview based on the eigenvalue approach (Fig. 6a) and on direct numerical simulations using the quantity E(t) (Fig. 7a). The stability behavior in Table 2 is derived from Figs. 6a and 7a. Figure 8 shows direct numerical simulations of the salt concentration for the cases 6, 7, and 8. In those simulations, we have used $\varDelta {\mathcal {M}} = \pi / 5 \!\approx \! 0.6$, $\varDelta t = 0.05$, and $N = 50000$ which corresponds to a (dimensionless) time horizon of 2500. Further, we perturb the initial concentration by a small symmetric (with respect to $x = 0$) perturbation of the form

$$\begin{aligned} C(x,z,0) = \epsilon \cos a_{1,1} x, \end{aligned}$$

(86)

in which $\epsilon = 0.001$.

Table 2 Overview of the selected geometries for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and their stability ($\mathrm{S} = \mathrm{stable}$, $\mathrm{U} = \mathrm{unstable}$ episode)

For ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, we have a fixed geometrical configuration (i.e., $a_{1,1} \!\equiv \! 1$). An overview of the stability results is shown in Table 3. There we present for different Rayleigh numbers a stability overview based on the eigenvalue approach (Fig. 6b) and on direct numerical simulations using the quantity E(t) (Fig. 7b).

Table 3 Overview of the selected system Rayleigh numbers for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ and their stability ($\mathrm{S} = \mathrm{stable}$, $\mathrm{U} = \mathrm{unstable}$ episode)

This time the stability behavior in Table 3 is derived from Fig. 6b. Figure 9 shows direct numerical simulations of the salt concentration for the cases 1, 7, and 8. In those simulations, we have used $\varDelta {\mathcal {M}} = 0.15$, $\varDelta t = 0.005$, and $N = 30{,}000$ which corresponds to a (dimensionless) time horizon of 150.

Figure 7a shows E over time for an $\ell _x$ range as given in Table 2. For $\ell _x = 5\pi$, we have a monotonically decreasing E, which means that the solution remains close to the ground state $C_0(z,t)$ and the discrete $L^2(\varOmega _A)$-norm of the perturbation decays in time. Growth is observed for $\ell _x > 7\pi$: there exists a time $t^*$ and $t^{**}$ for which

$$\begin{aligned} E'(t)< 0 \quad&\text {for }\;\;0< t< t^* , \\ E'(t)> 0 \quad&\text {for }\;\;t^*< t< t^{**} , \\ E'(t) < 0 \quad&\text {for }\;\;t > t^{**} . \end{aligned}$$

Here, $^{\prime }$ denotes the derivative with respect to time. The interval $(t^*, t^{**}$) is referred to as the unstable episode obtained by direct numerical simulations. Numerically, we find that it is consistent with the theoretical predicted range $(t_L(a_{1,1}), t_R(a_{1,1}))$, as given by Fig. 6.

$$\begin{aligned} t_L(a_{1,1})< t^*< t^{**} < t_R(a_{1,1}). \end{aligned}$$

For example, $\ell _x = 8\pi$ ($a_{1,1} = 0.125$) yields

$$\begin{aligned} \left( t_L(0.125), t_R(0.125)\right) = (13, 290) \quad \text {and} \quad (t^*, t^{**}) = (88, 277). \end{aligned}$$

Note that the threshold value $\ell _x = 7\pi$ is slightly larger than the theoretically predicted value of $6.82\pi$.

Figure 7b shows again E over time for an $R_S$ range as given by Table 3. For $R_S \!=\! 1$, we have a monotonically decreasing E(t), which means that the solution remains close to the ground state $C_0(z,t)$ and the discrete $L^2(\varOmega _B)$-norm of the perturbation decays in time. For the other two numerical experiments, we find

$$\begin{aligned} \left( t_L(1), t_R(1)\right)&= (0.024, 39.25) \quad \text {and} \quad (t^*, t^{**}) = (0.32, 7.7) \quad \text {for}\;\;R_S = 15,\;a_{1,1} = 1 , \\ \left( t_L(1), t_R(1)\right)&= (0.11, 84) \quad \text {and}\quad (t^*, t^{**}) = (0.17, 7.8) \quad \text {for }\;\;R_S = 20,\;a_{1,1} = 1 . \end{aligned}$$

Also note that for those two system Rayleigh numbers, the used wavenumber of the initial perturbation ($a = 1$) is relatively far away from its critical value 2.2 and 2.93, respectively (see also Fig. 6, right). As a result, the numerical bounds are not sharp with respect to their corresponding theoretical bounds.

Fig. 7

E(t) on a log–log scale, for a homogeneous porous column. a${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$, with data from Table 2. b${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, with data from Table 3

Remark 8

As shown in Fig. 7, quantity E decays to zero for large times, indicating that the system will return to some one-dimensional profile. However, this profile is not the one-dimensional ground-state solution due to the transient convective instability. The long-term one-dimensional profile can still be considered as the solution of (17), but with an adjusted initial condition.

The concentration profiles as function of time are presented in Fig. 8 for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$, and Fig. 9 for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$. In both cases, we observe for the selected cases transient instability. The instability introduces convective flow for a specific period of time. This convective dominated regime enhances the diffusive downward transport of salt into the porous column. The speed of the fingertips is higher for larger domains (${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$) and larger Rayleigh numbers (${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$). Along $\varGamma _3$, near the corners, there is upward flow. Such upward flow was observed experimentally by Webster et al. (1996). The combination of the concentration boundary condition along $\varGamma _3$ and upward flow leads near the corners to a thin concentration boundary layer.

Fig. 8

Concentration profiles as function of time for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$: a$\ell _x = 10\pi$, b$\ell _x = 11\pi$ and c$\ell _x = 12\pi$. For those geometrical configurations, initial perturbations decay, grow and eventually decay again in time, exhibiting a transient instability

Fig. 9

Concentration profiles as function of time for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$: a$R_S = 1.0$. This represents a stable configuration in which only diffusive transport takes place. b, c$R_S = 15$ and $R_S = 20$, respectively. Here again transient instabilities are observed

6.2 Layered Soils

Until now, we assumed for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ homogeneous media only. We now consider, for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ only, a heterogeneous medium having three layers, in which one of the layers has a reduced permeability. The layered permeability structure is represented by

$$\begin{aligned} \kappa (z) = {\left\{ \begin{array}{ll} {\underline{\kappa }} \quad \text {in }\;\;\left\{ (x,z) \in {\widehat{\varOmega }}_A^d : d_1< z< d_2, 0< d_1< d_2 < d\right\} \\ 1 \quad \text {elsewhere.} \end{array}\right. } \end{aligned}$$

Since the dimensional permeability is scaled by ${\overline{\kappa }}$, we have ${\underline{\kappa }} \!\leqslant \! 1$.

In each vertical layer, the permeability is assumed to be constant. Hence, in each layer a ‘local’ system Rayleigh number, denoted by $R_S^{{\underline{\kappa }}}$, can be defined. We consider two values for ${\underline{\kappa }}$: 0.5 and 0.05. The layer parameters $d_1$, $d_2$, and d are given by 3, 5 and 50, respectively. The initial condition is again symmetrically perturbed by (86) with $a_{1,1} \!\equiv \! 1$.

Fig. 10

Concentration profiles as function of time for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ with $R_S = 20$. The porous medium is divided into three layers: I, II, and III. Layer II has a different permeability, and is shown in gray. Layers I and III have permeability $\kappa \!=\! 1$. The following permeability values for layer II are considered: $\kappa = 1.0$ (a; for reference), $\kappa = 0.5$ (b), and $\kappa = 0.05$ (c)

Fig. 11

E(t) on a log–log scale, for a heterogeneous porous column. The numbers between brackets represent ${\underline{\kappa }}$ in layer II

The nature of the stream function ensures that continuity across the layer interface and yields continuity of the normal component of the fluid discharge. Hence, continuity of $\varPsi$ is the only condition imposed at those interfaces.

Numerical simulations for this three-layer setup are shown in Fig. 10 for a system Rayleigh number $R_S = 20$. This Rayleigh number corresponds to a system with a transient instability, see also Table 3: The perturbation develops in layer I until the fingertip reaches $z = d_1$, the start of the layer II. The finger pattern travels through layer II and as can be clearly seen for $t = 4$ and $t = 5$, the finger has become more narrow. For the special case in which layer II is almost impermeable, the convection cells in layer I develop and disappear over time again, whereas in layer III a reverse process takes place: No convection cells exist for small times, but for larger times they appear. However, for $R_S = 20$ those convection cells in layer III are too weak to create a finger structure. Ultimately, the finger structure disappears and diffusion becomes the dominant process again.

The effect of ${\underline{\kappa }}$ is also reflected by the stability measure E(t), as shown in Fig. 11. For smaller values of ${\underline{\kappa }}$, we observe a shorter episode of instability $(t^*, t^{**})$. Further, the magnitude of the growing instability is, as to be expected, less pronounced because the almost impermeable layer blocks the convective transport of the finger to deeper regions.

7 Interpretation in Terms of Dimensional Physical Parameters

Thus far the entire analytical and numerical analysis has been carried out in terms of dimensionless variables. In the concrete, dimensional world, the analysis covers a vast number of special cases. To interpret the results for specific cases, one has to return to dimensional variables by multiplying the dimensionless variables by the corresponding characteristic scales. We use subscript D to denote the dimensional variables. Specifically, multiplying the spatial dimensionless coordinates x, y, z by the characteristic length scale $L_\mathrm{c}$ gives spatial dimensional coordinates $x_D, y_D, z_D$ and multiplying the dimensionless time t by the characteristic time $T_\mathrm{c}$ gives the dimensional time $t_D$:

$$\begin{aligned} \{x_D, y_D, z_D\} = \{L_\mathrm{c} x, L_\mathrm{c} y, L_\mathrm{c} z\} \quad \mathrm{and} \quad t_D = T_\mathrm{c} t. \end{aligned}$$

(87)

Also of interest are the dimensional wave number $a_D$ and wave length $\lambda _D$ given by

$$\begin{aligned} a_D = a L_\mathrm{c}^{-1} \quad \mathrm{and} \quad \lambda _D = L_\mathrm{c} \lambda \quad \text {where} \quad \lambda _D = \frac{2\pi }{a_D}. \end{aligned}$$

(88)

To illustrate the conversion, we use the typical values of quantities listed in Table 4. Introducing the values of $\phi$, $\rho _\mathrm{f}$, $\rho _\mathrm{s}$, g, $\mu$, $\kappa _\mathrm{c}$ and D from Tables 4 in  1 gives the characteristic scales for discharge ($Q_\mathrm{c}$), length ($L_\mathrm{c}$), time ($T_\mathrm{c}$), pressure ($P_\mathrm{c}$), and Rayleigh number R. If $\kappa _\mathrm{c}$ is left to be chosen, then Table 5 results.

Motivated by solute exchange by convection within estuarine sediments, Webster et al. (1996) made an experimental and numerical analysis of unstable penetration of ponded saline water into a layer of porous medium initially saturated with freshwater, using $\kappa _\mathrm{c} = 5.4 \times 10^{-11}\,\mathrm{m}^2$. Post and Kooi (2003), Post (2004) numerically modeled the rates of salinization in the high-permeability Pleistocene coastal aquifer of the Netherlands, using $\kappa _\mathrm{c} = 10^{-11}\,\mathrm{m}^2$. More or less in line with those values of $\kappa _\mathrm{c}$, we consider in the first instance a porous medium with $\kappa _\mathrm{c} = 10^{-12}\,\mathrm{m}^2$ and subsequently infer results for coarser porous media with larger values of $\kappa _\mathrm{c}$ and for finer porous media with lower values of $\kappa _\mathrm{c}$. Substitution of $\kappa _\mathrm{c} = 10^{-12}\,\mathrm{m}^2$ in Table 5 gives the values of $Q_\mathrm{c}$, $L_\mathrm{c}$, $T_\mathrm{c}$, $P_\mathrm{c}$ and R in Table 6.

Table 4 Typical values or ranges of values of physical quantities, using the International System of Units (SI)

Table 5 Overview of parameters for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ obtained by substitution in Table 1 the values for $\phi$, $\rho _\mathrm{f}$, $\rho _\mathrm{s}$, g, $\mu$ and D from Table 4

Table 6 Overview of parameters for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ obtained by setting $\kappa _\mathrm{c} = 10^{-12} \mathrm{m}^2$ in Table 5

7.1 Laterally Unbounded ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$

According to Table 5 (left column), for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ the Rayleigh number $R = 1$ and the characteristic scales $Q_\mathrm{c}$, $L_\mathrm{c}$, $T_\mathrm{c}$ and $P_\mathrm{c}$ are proportional to powers of the characteristic permeability $\kappa _\mathrm{c}$. To the wide range of values of $\kappa _\mathrm{c}$ in Table 4 from 10$^{-10}$ m$^2$ for very coarse porous media to 10$^{-16}$ m$^2$ for very fine porous media correspond wide ranges of the values of the scales $Q_\mathrm{c}$, $L_\mathrm{c}$, $T_\mathrm{c}$ and $P_\mathrm{c}$.

The approximate equality of the stability bounds from the linear and energy stability led for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ to the dimensionless condition (74) for $L^2$-stability:

$$\begin{aligned} a_{1,1} = \sqrt{\left( \frac{\pi }{\ell _x}\right) ^2 + \left( \frac{\pi }{\ell _y}\right) ^2} \geqslant \frac{1}{6.82}. \end{aligned}$$

(89)

In dimensional variables, this is equivalent to:

$$\begin{aligned} a_{1,1,D} = \sqrt{\left( \frac{\pi }{\ell _x}\right) ^2 + \left( \frac{\pi }{\ell _y}\right) ^2}L_\mathrm{c}^{-1} \geqslant \frac{L_\mathrm{c}^{-1}}{6.82}, \end{aligned}$$

where $L_\mathrm{c}$ given by the left-hand side column in Table 5. Only perturbations with wave numbers that are smaller will grow and decay in a certain time interval $t_{L,D} = T_\mathrm{c} t_L$ to $t_{R,D} = T_\mathrm{c} t_R$, where $t_L$ and $t_R$ can be read from Fig. 6a. The corresponding condition for the wave length is derived from (89):

$$\begin{aligned} \lambda _D = \frac{2\pi }{a_{1,1,D}} \leqslant 42.85 L_\mathrm{c}. \end{aligned}$$

Only perturbations with wave lengths that are larger will grow and decay in a certain time interval $t_{L,D} = T_\mathrm{c} t_L$ to $t_{R,D} = T_\mathrm{c} t_R$.

Using the values in the left column of Tables 6 and 2 is translated to dimensional form by multiplying $\ell _x$ and d by $L_\mathrm{c} = 6 \times 10^{-3}\,\mathrm{m}$. Figure 7a is translated to dimensional form by multiplying the t-axis by $T_\mathrm{c} = 8.4 \times 10^3\,\mathrm{s}$ and $\ell _x$ by $L_\mathrm{c} = 6 \times 10^{-3}\,\mathrm{m}$. The dimensionless numerical results shown in Fig. 8 are be translated to dimensional form by multiplying the depth $d = 250$ and the column width $\ell _x = 10, 11,$ and 12 by $L_\mathrm{c} = 6 \times 10^{-3}\,\mathrm{m}$, giving $d_D = 1.5\,\mathrm{m}$ and $\ell _{xD} = 6.0, 6.6, 7.2\,\mathrm{cm}$ and the times $t = 200, 500, \ldots , 3500$ by $T_\mathrm{c} = 8.4 \times 10^3\,\mathrm{s}$ giving $t_D = 24.25, 48.50,\ldots , 339$ days.

For a finer porous medium with a tenfold smaller value $\kappa _\mathrm{c} = 10^{-13} \mathrm{m^2}$, the values of $\ell _{xD} = 60, 66, 72\,\mathrm{cm}$ are tenfold larger and the values of $t_D = 6.64, 13.29, \ldots , 93.01$ years are 100-fold larger.

For a coarser porous medium with a tenfold larger value $\kappa _\mathrm{c} = 10^{-11}\,\mathrm{m^2}$, the values of $\ell _{xD} = 6.0, 6.6, 7.2\,\mathrm{mm}$ are tenfold smaller and the values of $t_D = 0.2425, 0.4850, \ldots ,$ 3.3950 days are 100-fold smaller. For still coarser porous media, the width of the fingers will eventually be of the same order as the size of the pores, so that the limit of the Darcy model will be approached.

7.2 Laterally Bounded ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$

According to Table 5 (right column), for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, the characteristic length scale $L_\mathrm{c}$ and pressure scale $P_\mathrm{c}$ and the Rayleigh number R depend linearly on the horizontal length scale $L_x$, while for the timescale $T_\mathrm{c}$ this dependence is quadratic; further, the flux scale $Q_\mathrm{c}$ and R are proportional to $\kappa _\mathrm{c}$. With the wide range of values of $\kappa _\mathrm{c}$ in Table 4, the corresponding wide range of values of the Rayleigh number R is $53.05 \times 10^2 L_x$ for very coarse porous media to $53.05 \times 10^{-4} L_x$ for very fine porous media.

From the expression for R in Table 5 (right column), it follows that:

$$\begin{aligned} L_x = 1.89 \times 10^{-14} {\kappa _\mathrm{c}}^{-1} R \quad \mathrm{(m)}. \end{aligned}$$

(90)

Introducing (90) in the expressions for characteristic length scale $L_\mathrm{c}$ and timescale $T_\mathrm{c}$ in Table 5 (right column) gives:

$$\begin{aligned} L_\mathrm{c} = 6.02 \times 10^{-15} {\kappa _\mathrm{c}}^{-1} R \quad \mathrm{(m)},\! \quad \mathrm{i.e.,}\! \quad L_\mathrm{c} = 6.02 \times 10^{-3} R \quad \mathrm{(m)}\! \quad \! \mathrm{if} \quad \kappa _\mathrm{c} = 10^{-12} \quad (\mathrm{m}^2), \end{aligned}$$

(91)

and

$$\begin{aligned} T_\mathrm{c} = 8.323 \times 10^{-21} {\kappa _\mathrm{c}}^{-1} R^2\! \quad \! \mathrm{(s),}\! \quad \! \mathrm{i.e.,} \quad T_\mathrm{c} = 8.323 \times 10^{-9} R^2 \quad \mathrm{(s)}\! \quad \! \mathrm{if} \quad \kappa _\mathrm{c} = 10^{-12} \quad (\mathrm{m}^2). \end{aligned}$$

(92)

For a finer porous medium with a tenfold smaller permeability $\kappa _\mathrm{c} = 10^{-13}\,\mathrm{m^2}$, the values of $L_\mathrm{c}$ are tenfold larger and the values of $T_\mathrm{c}$ are 100-fold larger. For a coarser porous medium with a tenfold larger permeability $\kappa _\mathrm{c} \!=\! 10^{-11}\,\mathrm{m^2}$, the values of $L_\mathrm{c}$ are tenfold smaller and the values of $T_\mathrm{c}$ are 100-fold smaller.

The approximate equality of the stability bounds from the linear and energy methods led for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ to the dimensionless condition (75) for $L^2$-stability:

$$\begin{aligned} a_{1,1} = \sqrt{1 + \left( \frac{1}{\ell }\right) ^2} \geqslant \frac{R_S}{6.82}. \end{aligned}$$

(93)

Here, $\ell$ represents the aspect ratio of a rectangular box $(0,L_x) \times (0, L_y)$, i.e., $\ell = L_y / L_x$. In dimensional variables, this is equivalent to:

$$\begin{aligned} a_{1,1,D} = \sqrt{1 + \left( \frac{L_x}{L_y}\right) ^2}L_\mathrm{c}^{-1} \geqslant \frac{R_S L_\mathrm{c}^{-1}}{6.82}, \end{aligned}$$

where $L_\mathrm{c}$ given by the right-hand side column in Table 5. Only perturbations with wave numbers that are smaller will grow and decay in a certain time interval $t_{L,D} = T_\mathrm{c} t_L$ to $t_{R,D} = T_\mathrm{c} t_R$, where $t_L$ and $t_R$, for a given $R_S$, can be read from Fig. 6b. The corresponding condition for the wave length is derived from (93):

$$\begin{aligned} \lambda _D = \frac{2\pi }{a_{1,1,D}} \leqslant 42.85 L_\mathrm{c} R_S^{-1}. \end{aligned}$$

Only perturbations with wave lengths that are larger will grow and decay in a certain time interval $t_{L,D} = T_\mathrm{c} t_L$ to $t_{R,D} = T_\mathrm{c} t_R$.

Criterion (93) means that in a rectangular column the ground state is $L^2$-stable provided

$$\begin{aligned} R_S < 6.82\sqrt{1 + \frac{1}{\ell ^2}}, \end{aligned}$$

(94)

or, using Table 1,

$$\begin{aligned} \frac{\kappa _\mathrm{c}(\rho _\mathrm{s} - \rho _\mathrm{f})gL_x}{\mu D} < 21.43\sqrt{1 + \frac{1}{\ell ^2}}. \end{aligned}$$

(95)

When the cross section is a square, i.e., $\ell = 1$, $L^2$-stability holds if

$$\begin{aligned} \frac{\kappa _\mathrm{c}(\rho _\mathrm{s} - \rho _\mathrm{f})gL_x}{\mu D} < 30.30. \end{aligned}$$

(96)

In practice, experiments are often performed in cylindrical columns see, e.g., Wooding (1959). Suppose we consider in ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ a semi-infinite cylinder of radius ${\mathcal {R}}$. This radius will then be used, conform ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, in the characteristic length scale $L_\mathrm{c} = \frac{{\mathcal {R}}}{\pi }$. Then, instead of (36), we have

$$\begin{aligned} \varOmega _B = \left\{ (x,y,z) : \sqrt{x^2 + y^2} < \pi , z > 0 \right\} . \end{aligned}$$

As in (33), we need to consider now the eigenvalue problem

In particular, for the given geometry, one needs to determine the smallest $a > 0$ for which the eigenvalue problem (97) has a solution. As explained in Sect. 6.1.2, this solution describes the most unstable mode.

Solutions of ((97a)) are found by separation of variables:

$$\begin{aligned} f(r,\varphi ) = J_m(ar)\cos m\varphi , \end{aligned}$$

(98)

where $J_m$ denotes the Bessel function of the first kind of order m. Boundary condition ((97b)) is satisfied when

$$\begin{aligned} J'_m(a\pi ) = 0 \quad ('\text { denotes differentiation)}, \end{aligned}$$

or

$$\begin{aligned} a = a_{n,m} = \frac{\beta _{n,m}}{\pi } \quad n=1,2,\ldots \quad \text {and} \quad m=0,1,2,\ldots , \end{aligned}$$

where $\beta _{n,m}$ is the $n{\mathrm{th}}$ positive zero of $J_m'$. Clearly

$$\begin{aligned} \min _{\begin{array}{c} n=1,2,\ldots \\ m=0,1,2,\ldots \end{array}} \beta _{n,m} = \min _{m=0,1,2,\ldots }\beta _{1,m}. \end{aligned}$$

Looking up the zeros of $J_m'$ in Weisstein (2018) gives

$$\begin{aligned} \min _{m=0,1,2,\ldots }\beta _{1,m} = \beta _{1,1} = 1.8412. \end{aligned}$$

This yields $a = {\hat{a}}_{1,1} = \frac{\beta _{1,1}}{\pi }$ as the smallest $a > 0$ for which (97) has a nontrivial solution. Using ${\hat{a}}_{1,1}$ in (93) yields for cylinders the stability criterion

$$\begin{aligned} \frac{\kappa _\mathrm{c} (\rho _\mathrm{s} - \rho _\mathrm{f}) g {\mathcal {R}}}{\mu D} < 12.56. \end{aligned}$$

(99)

Flow patterns corresponding to (98) are discussed in Pieters et al. (2018).

The dimensionless time axis of Fig. 7 for the stability measures E is translated to a dimensional time axis by multiplying it by the characteristic time $T_\mathrm{c}$ given by (92). Since $T_\mathrm{c}$ is proportional to $R_S^2$, the tendency is that the transient instability occurs later for larger $R_S$.

The dimensionless numerical results shown in Fig. 9 are be translated to dimensional form by multiplying the dimensionless depth $d = 75$ and column width $2\pi$ by the linearly R dependent characteristic length $L_\mathrm{c}$ given by (91) and multiplying the dimensionless times $t = 1, 2, 3 , 4, 5, 10, 15, 20, 30, 35$ by the quadratically R dependent characteristic time $T_\mathrm{c}$ is given by (92).

8 Conclusions

We analyzed the stability of the density-depth profiles in porous media initially saturated with a stagnant fluid of density $\rho _\mathrm{f}$ after flooding with a salt solution of higher density $\rho _\mathrm{s}$. Such flooding of coastal areas with seawater regularly occurs, either due to climatological circumstances or as part of engineering projects. Historically, flooding was sometimes also imposed as a defensive measure.

We used the standard convection–diffusion equation subject to the so-called Boussinesq approximation. The variable density arising from the diffusive penetration of salt then affects the fluid flow only by its effect on the gravitational driving force in the Darcy equation. To explore the density difference-induced flow, we used both analytical and numerical methods. We assumed the depth of the porous medium to be infinite in the analytical approaches and finite in the numerical analyses. Geometrically, two cases were distinguished: the laterally unbounded ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and the laterally bounded ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$. The ratio of the diffusivity D and the density difference-induced gravitational shear flow $(\kappa _\mathrm{c} / \mu ) (\rho _\mathrm{s}-\rho _\mathrm{f})g$ is an intrinsic length scale of the problem. In the unbounded ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$, this is the only length scale and using it leads to a dimensionless formulation with Rayleigh number $R \!=\! 1$. In the bounded ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, the lateral geometry provides another length scale and using it leads to a dimensionless formulation with a Rayleigh number R given by the ratio of the geometric and intrinsic length scales.

The analytical approaches lead to general statements about stability or instability under given circumstances. The background diffusion of salt from the ponded layer into the fluid saturated porous medium, the so-called ground-state solution, is expressed in terms of the Boltzmann similarity variable $z/\sqrt{t}$. Three methods were used to study the stability of this ground state, the first two based on the linearized perturbation equation for the concentration and the third based on the full nonlinear perturbation equation. They yield eigenvalue problems that contain the horizontal wave number a and the Rayleigh number R as parameters. For homogeneous soils, using the Boltzmann variable $z/\sqrt{t}$, the time t can be eliminated from the eigenvalue problem by absorbing $\sqrt{t}$ into a and R: $b = a\sqrt{t}$ and $R^* \!=\! R\sqrt{t}$. This time-independence of the eigenvalue problems leads to the three stability curves relating the transformed Rayleigh number $R^*$ and wave number b shown in Fig. 4.

For the first linear approach, the surface spatial density gradient was used as an approximation of the entire background density profile. This results in a crude estimate of the $L^2$-norm of the concentration shown in Fig. 3, with the perturbation at first growing, but eventually decaying in time.

For the second linear approach, the full ground-state solution subject to the restriction that the ground state slowly evolves in time was used: the so-called frozen profile approximation. This method of linearized stability only holds for infinitesimal perturbations. To get results for larger perturbations, a specific version of the variational energy method was used to estimate from the full nonlinear perturbation equation the $L^2$-norm of the concentration perturbation c. The stability curve $R^*_L(b)$ resulting from the linearized perturbation approach is surprisingly close to the stability curve $R^*_E(b)$ resulting from the variational energy method. This means that there is only a small gap between stability curves $R^*_L(b)$ and $R^*_E(b)$ in which small perturbations vanish, but large perturbations may grow. In this respect, the current problem differs markedly from the problem with an imposed vertical background flow analyzed earlier (van Duijn et al. 2002), for which the gap was found to be large. The ponded problem considered in this paper has a sharp stability bound: below $R^*_E$ there is unconditional stability and above $R^*_L$ instability. The curve $R^*_M = b^2$ resulting from the first linear approach is shown to be a lower bound for both $R^*_L$ and $R^*_E$.

For both ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$, the $\sqrt{t}$ transformed system Rayleigh number $R^*_S = R_S \sqrt{t}$ is a linear function of the $\sqrt{t}$ transformed system wave number b. To determine the stability for a particular wave number b - system Rayleigh number $R_S$ combination, three cases can be distinguished, depending on whether the straight line $R^*_S = \alpha b$ lies entirely below $R^*_E$, touches $R^*_E$ at $b = b^*$, or intersects $R^*_E$ at $b^*_L$ and $b^*_R$. Numerically, it was found that the line with $\alpha = \alpha _{\mathrm{crit}} = 3.85$ touches $R^*_E$ at $(R^*, b) = (3.89, 1.01)$. For $\alpha < \alpha _{\mathrm{crit}}$ the ground state is unconditionally stable. For $\alpha > \alpha _{\mathrm{crit}}$, the ground state is unconditionally stable for $b < b^*_L$ and $b > b^*_R$ and experiences an episode of transient instability for $b^*_L< b < b^*_R$.

In Sect. 6.1.2, by reversal of the Boltzmann transformations, the analytical stability results were interpreted for both ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ in terms of system Rayleigh number $R_S$, wave number a and time t (see in particular Fig. 6). In Sect. 6.1.3, these results were compared with direct numerical simulations based on the full, spatially 2-D flow and transport equations in x, z, t, with a range of lateral length scales for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ (see Table 2) and a range of system Rayleigh numbers for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ (see Table 3). Qualitatively, the numerical results turned out to agree with the eigenvalue results. They also clearly show the details of the transient instabilities as function of the wave number for ${{{\mathbf {{\small {\uppercase {case~A}}}}}}}$ and of the wave number and system Rayleigh number for ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$. The transient instability clearly leads to deeper penetration of salt.

The case of a layered soil was considered in Sect. 6.2. There the Boltzmann transformation does not apply and one has to rely on numerical techniques. Results of the salt distribution in an aquifer having a horizontal and lower permeable layer are shown in Fig. 10. This figure clearly demonstrates the effect of the layer acting as a barrier for the flow and thus for the salt transport. This illustrates the protective role of low-permeability layers against invasion of saline water into underlying freshwater mentioned in the Introduction.

In Sect. 7, it was shown how the dimensionless analytical and numerical results can be translated to dimensional form and thereby interpreted in terms of dimensional length and time scales. This provided an opportunity to highlight the important role of the permeability of the porous medium: The higher the permeability the stronger is the destabilizing influence of the gravitational force.

The laterally bounded ${{{\mathbf {{\small {\uppercase {case~B}}}}}}}$ with its no-flow and no-solute transport conditions at the vertical boundary $\varGamma _\nu$ is not restricted to rectangles and hexagons, but covers columns of any shape, such as the cylinders discussed at the end of Sect. 7. Thus, it provides a good basis for the interpretation of experiments in columns. In particular, column experiments are stable provided, see also (95), (96), and (99):

• (i) Rectangular cross section $(0,L_x)\times (0,L_y)$

  $$\begin{aligned} \frac{\kappa _\mathrm{c}(\rho _\mathrm{s} - \rho _\mathrm{f})g L_x}{\mu D} < 21.43\sqrt{1 + \frac{1}{\ell ^2}}, \quad \ell = \frac{L_y}{L_x}; \end{aligned}$$

• (ii) Square cross section $(0,L_x)\times (0,L_x)$

  $$\begin{aligned} \frac{\kappa _\mathrm{c}(\rho _\mathrm{s} - \rho _\mathrm{f})g L_x}{\mu D} < 30.30; \end{aligned}$$

• (iii) Circular cross section with radius ${\mathcal {R}}$

  $$\begin{aligned} \frac{\kappa _\mathrm{c}(\rho _\mathrm{s} - \rho _\mathrm{f})g {\mathcal {R}}}{\mu D} < 12.56. \end{aligned}$$