Skip to main content
SpringerLink
Log in

Mathematical Modeling on Mobility and Spreading of BTEX in a Discretely Fractured Aquifer System Under the Coupled Effect of Dissolution, Sorption, and Biodegradation

  • Published:
Transport in Porous Media Aims and scope Submit manuscript

Abstract

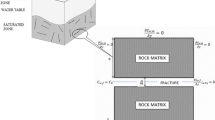
This paper presents a numerical model to investigate the migration of BTEX (benzene, toluene, ethylbenzene, and xylene) within a fractured aquifer system at the scale of a single fracture under the coupled effect of various transport processes such as dissolution, sorption, biodegradation. The developed model also considers the influence of equilibrium- and kinetic-controlled sorption scenarios on BTEX transport. Further, the transport characteristics of dissolved BTEX within the fracture–matrix system (FMS) are obtained by carrying out the spatial moment analysis on the concentration profiles simulated. In this study, the spatial moment analysis is conducted to estimate the following transport characteristics of dissolved BTEX: (a) velocity within the fracture, (b) dispersion coefficient within the fracture, (c) dissolved mass within the matrix. In order to investigate the sensitivity of various input parameters, two sensitivity indices are computed based on the variation in the velocity of dissolved BTEX constituent within the fracture (SI_vel) and on the variation in the dissolved mass of BTEX constituents within the matrix (SI_mat). Results from the present simulation study suggest that the sorption and biodegradation reactions influence the concentration distribution of highly soluble BTEX constituents (benzene, toluene) within the FMS significantly. The influence of biodegradation on the migration of BTEX within the FMS is found to be more when it co-occurs with the sorption reaction. The effect of sorption and biodegradation reactions on the mobility and dispersion coefficient of dissolved BTEX constituents within the FMS is found to be significant during the early simulation period.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  • Arnon, A., Adar, E., Ronen, Z., Yakirevich, A., Nativ, R.: Impact of microbial activity on the hydraulic properties of fractured chalk. J. Contam. Hydrol. 76, 315–336 (2005)

    Article  Google Scholar 

  • Atteia, O., Guillot, C.: Factors controlling BTEX and chlorinated solvents plume length under natural attenuation conditions. J. Contam. Hydrol. 90, 81–104 (2007)

    Article  Google Scholar 

  • Bear, J., Tsang, C.F., De Marsily, G.: Flow and Contaminant Transport in Fractured Rock. Academic Press Inc., San Diego (2012)

    Google Scholar 

  • Bekins, B.A., Cozzarelli, I.M., Cozzarelli, I.M., Godsy, E.M., Warren, E., Essaid, H.I., Tuccillo, M.E.: Progression of natural attenuation processes at a crude oil spill site: II. Controls on spatial distribution of microbial populations. J. Contam. Hydrol. 3–4, 387–406 (2001a)

    Article  Google Scholar 

  • Bekins, B.A., Rittmann, B.E., MacDonald, J.A.: Natural attenuation strategy for groundwater cleanup focuses on demonstrating cause and effect. EOS Trans. AGU 53, 57–58 (2001b)

    Google Scholar 

  • Berkowitz, B., Zhou, J.: Reactive solute transport in a single fracture. Water Resour. Res. 4, 901–913 (1996)

    Article  Google Scholar 

  • Bodin, J., Delay, F., de Marsily, G.: Solute transport in fissured aquifers: 1. Fundamental mechanisms. Hydrogeol. J. 11, 418–433 (2003a)

    Article  Google Scholar 

  • Bodin, J., Delay, F., de Marsily, G.: Solute transport in a single fracture with negligible matrix permeability: 2. Mathematical formalism. Hydrogeol. J. 11, 434–454 (2003b)

    Article  Google Scholar 

  • Bradley, P.M., Journey, C.A., Kirshtein, J.D.: Enhanced dichloroethene biodegradation in fractured rock under biostimulated and bioaugmented conditions. Remed. J. 2, 21–32 (2012)

    Article  Google Scholar 

  • Chambon, J.C., Broholm, M.M., Binning, P.J., Bjerg, P.L.: Modeling multi-component transport and enhanced anaerobic dechlorination processes in a single fracture–clay matrix system. J. Contam. Hydrol. 112, 77–90 (2010)

    Article  Google Scholar 

  • Chapelle, F.H., Widdowson, M.A., Brauner, J.S., Mendez, E., Casey, C.C.: Methodology for Estimating Times of Remediation Associated with Monitored Natural Attenuation. United States Geological Survey Water Resources Investigations Report. 03-4057 (2003)

  • Cherubini, C., Pastore, N., Giasi, C.I., Allegretti, N.M.: Laboratory experimental investigation of heat transport in fractured media. Nonlinear Process. Geophys. 24, 23–42 (2017)

    Article  Google Scholar 

  • Declercq, I., Cappuyns, V., Duclos, Y.: Monitored natural attenuation (MNA) of contaminated soils: state of the art in Europe—a critical evaluation. Sci. Total Environ. 1, 393–405 (2012)

    Article  Google Scholar 

  • Detwiler, R.L., Rajaram, H., Glass, R.J.: Nonaqueous-phase-liquid dissolution in variable-aperture fractures: development of a depth-averaged computational model with comparison to a physical experiment. Water Resour. Res. 37(12), 3115–3129 (2001)

    Article  Google Scholar 

  • Detwiler, R.L., Rajaram, H., Glass, R.J.: Interphase mass transfer in variable aperture fractures: controlling parameters and proposed constitutive relationships. Water Resour. Res. 45, W08436 (2009)

    Article  Google Scholar 

  • Dickson, S.E., Thomson, N.R.: Dissolution of entrapped DNAPLs in variable aperture fractures: experimental data and empirical model. Environ. Sci. Technol. 37(18), 4128–4137 (2003)

    Article  Google Scholar 

  • Essaid, H.I., Cozzarelli, M.I., Eganhouse, P.R., Herkelrath, W.N., Belkins, B.A., Delin, G.N.: Inverse Modeling of BTEX dissolution and biodegradation at the Bemidgi, M-N crude-oil spill site. J. Contam. Hydrol. 67, 269–299 (2003)

    Article  Google Scholar 

  • Faybishenko, B., Witherspoon, P., Bodvarsson, G.: Emerging issues in fractured-rock flow and transport investigations: introduction and overview. Dyn Fluids Transp Fract Rocks 162, 1–11 (2005)

    Google Scholar 

  • Geller, G.T., Holman, H.Y., Su, G., Conrad, M.E., Pruess, K., Hunter-Cevera, J.C.: Flow dynamics and potential for biodegradation of organic contaminants in fractured rock vadose zones. J. Contam. Hydrol. 1, 63–90 (2000)

    Article  Google Scholar 

  • Goltz, M.N., Roberts, P.V.: Using the method of moments to analyze three-dimensional diffusion-limited solute transport from temporal and spatial perspectives. Water Resour. Res. 23(8), 1575–1585 (1987)

    Article  Google Scholar 

  • Grisak, G.E., Pickens, J.F., Cherry, J.A.: Solute transport through fractured media 2. The column study of fractured till. Water Resour. Res. 4, 731–739 (1980)

    Article  Google Scholar 

  • Hansen, S.K., Kueper, B.H.: A new model for coupled multicomponent NAPL dissolution and aqueous-phase transport, with application to creosote dissolution in discrete fractures. Water Resour. Res. 50, 58–70 (2014)

    Article  Google Scholar 

  • Hardisty, P.E., Wheater, H., Johnston, P.M., Dabrowski, T.L.: Mobility of LNAPL in fractured sedimentary rocks: implications for remediation. In: Proceedings API/NGWA Conference on Hydrocarbons and Organic Chemicals in Groundwater, Houston (1994)

  • Hölttä, P., Hakanen, M., Hautojärvi, A., Timonen, J., Väätäinen, K.: The effects of matrix diffusion on radionuclide migration in rock column experiments. J. Contam. Hydrol. 21, 1–4 (1996)

    Article  Google Scholar 

  • Jacobson, G.: Pollution of a fractured rock aquifer by petrol a case study. BMR J. Aust. Geol. Geophys. 8, 313–322 (1983)

    Google Scholar 

  • Jørgensen, P.R., Helstrup, T., Urup, J., Seifert, D.: Modeling of non-reactive solute transport in fractured clayey till during variable flow rate and time. J. Contam. Hydrol. 68(3–4), 193–216 (2004)

    Article  Google Scholar 

  • Joshi, N., Ojha, C.S.P., Sharma, P.K.: A nonequilibrium model for reactive contaminant transport through fractured porous media: model development and semi analytical solution. Water Resour. Res. 48, W10511 (2012)

    Article  Google Scholar 

  • Joshi, N., Ojha, C.S.P., Sharma, P.K., Madramootoo, C.A.: Application of nonequilibrium fracture matrix model in simulating reactive contaminant transport through fractured porous media. Water Resour. Res. 51, 390–408 (2015)

    Article  Google Scholar 

  • Kischinhevsky, M., Paes-leme, P.J.: Modelling and numerical simulations of contaminant transport in naturally fractured porous media. Transp. Porous Med. 26, 25 (1997)

    Article  Google Scholar 

  • Knorr, B., Maloszewski, P., Krämer, F., Stumpp, C.: Diffusive mass exchange of non-reactive substances in dual-porosity porous systems—a column experiment under saturated conditions. Hydrol. Process. 30(6), 914–926 (2016)

    Article  Google Scholar 

  • Kolditz, O.: Modelling flow and heat transfer in fractured rocks: dimensional effect of matrix heat diffusion. Geothermics 24(3), 421–437 (1995)

    Article  Google Scholar 

  • Krooss, B.M., Leythaeuser, D.: Experimental measurements of the diffusion parameters of light hydrocarbons in water-saturated sedimentary rocks—ll. Results Geochem. Signif. Org. Geochem. 2, 91–108 (1988)

    Article  Google Scholar 

  • Lu, G., Clement, P.T., Zheng, C., Wiedemeier, H.T.: Natural attenuation of BTEX compounds: model development and field-scale applications. Ground Water 37, 707–717 (1999)

    Article  Google Scholar 

  • Lundegard, P.D., Johnson, P.C.: Source zone natural attenuation at petroleum hydrocarbon spill sites—II: application to a former oil field. Groundw Monit Remed. 4, 93–106 (2006)

    Article  Google Scholar 

  • Maloszewski, P., Zuber, A.: Mathematical modeling of tracer behavior in short-term experiments in fissured rocks. Water Resour. Res. 7, 1517–1528 (1990)

    Article  Google Scholar 

  • Molson, J.W., Frind, E.O., van Stempvoort, D.R., Lesage, S.: Humic acid-enhanced remediation of an emplaced diesel source in groundwater 2: numerical model development and application. J. Contam. Hydrol. 54, 277–305 (2002)

    Article  Google Scholar 

  • Mulligan, C.N., Yong, R.N.: Natural attenuation of contaminated soils. Environ. Int. 4, 587–601 (2004)

    Article  Google Scholar 

  • Mutch, R.D., Scott, J.I., Wilson, D.J.: Cleanup of fractured rock aquifers: implications of matrix diffusion. Environ. Monit. Assess. 24, 45 (1993)

    Article  Google Scholar 

  • Natarajan, N., Suresh Kumar, G.: Numerical modeling and spatial moment analysis of thermal fronts in a coupled fracture-skin-matrix system. Geotech. Geolog. Eng. 29(4), 477–491 (2011)

    Article  Google Scholar 

  • Neretnieks, I.: Diffusion in the rock matrix: an important factor in radionuclide retardation? J. Geophys. Res. 85, 4379–4397 (1980)

    Article  Google Scholar 

  • Neretnieks, I., Eriksen, T., Tahtimen, P.: Tracer movement in a single fissure in granite rock: some experimental results and their interpretation. Water Resour. Res. 4, 849–858 (1982)

    Article  Google Scholar 

  • Ordencrantz, J.E., Valocchi, A.J., Rittman, B.E.: Modeling the interaction of sorption and biodegrdation on transport in groundwater in situ bioremediation systems; In: Proceedings of the Groundwater Modeling Conference, Golden Colorado (1993)

  • Prommer, H., Barry, D.A., Davis, G.B.: A one-dimensional reactive multi component transport model for biodegradation of petroleum hydrocarbons. Environ. Modell. Softw. 14, 213–223 (1999)

    Article  Google Scholar 

  • Renu, V., Suresh Kumar, G.: Numerical modeling and spatial moment analysis of solute mobility and spreading in a coupled fracture-skin-matrix system. Geotech. Geolog. Eng. 30, 1289–1302 (2012)

    Article  Google Scholar 

  • Renu, V., Suresh Kumar, G.: Numerical modeling on benzene dissolution into groundwater and transport of dissolved benzene in a saturated fracture–matrix system. Environ. Process. 3(4), 781–802 (2016)

    Article  Google Scholar 

  • Renu, V., Suresh Kumar, G.: Benzene dissolution and transport in a saturated sinusoidal fracture with non-uniform flow: numerical investigation and sensitivity analysis. Environ. Process. 4(3), 587–601 (2017a)

    Article  Google Scholar 

  • Renu, V., Suresh Kumar, G.: Multi-component transport of BTX in a discretely fractured aquifer with fracture–skin: numerical investigation and sensitivity analysis. Environ. Earth Sci. 76, 619 (2017b)

    Article  Google Scholar 

  • Sekhar, M., Suresh Kumar, G.: Modeling transport of linearly sorbing solutes in a single fracture: asymptotic behavior of solute velocity and dispersivity. Geotech. Geol. Eng. 24(1), 183–201 (2006)

    Article  Google Scholar 

  • Scow, K.M., Hicks, K.A.: Natural attenuation and enhanced bioremediation of organic contaminants in groundwater. Curr. Opin. Biotech. 3, 246–253 (2005)

    Article  Google Scholar 

  • Sharma, P., Sekhar, M., Srivastava, R., Ojha, C.: Temporal moments for reactive transport through fractured impermeable/permeable formations. J. Hydrol. Eng. 12, 1302–1314 (2012)

    Article  Google Scholar 

  • Suresh Kumar, G.: Mathematical modeling of groundwater flow and solute transport in saturated fractured rock using a dual-porosity approach. J. Hydrol. Eng. 19(12), 04014033 (2014a)

    Article  Google Scholar 

  • Suresh Kumar, G.: Mathematical modelling on transport of petroleum hydrocarbons in saturated fractured rocks. Sadhana 39(5), 1119–1139 (2014b)

    Article  Google Scholar 

  • Tang, D.H., Frind, E.O., Sudicky, E.A.: Contaminant transport in fractured porous media: analytical solutions for a single fracture. Water Resour. Res. 17, 555–564 (1981)

    Article  Google Scholar 

  • Tsang, C., Neretneiks, I.: Flow channeling in heterogeneous fractured rocks. Rev. Geophys. 36, 275–298 (1998)

    Article  Google Scholar 

  • U.S.EPA: A citizen’s guide to natural attenuation. EPA 542-F-96-015. http://www.epa.gov/swertio1/download/remed/citguide/natural.html (1996)

  • Veettil, R.T., Suresh Kumar, G.: Numerical modeling on the sensitivity of directional dependent interface heat transfer on thermal transport in a coupled fracture–matrix system. Geosci. J. 20(5), 639–647 (2016)

    Article  Google Scholar 

  • Wu, Y., Ye, M., Sudicky, E.A.: Fracture-flow-enhanced matrix diffusion in solute transport through fractured porous media. Transp. Porous Med. 81, 21–34 (2009)

    Article  Google Scholar 

  • Yang, Z., Niemi, A., Fagerlund, F., Illangasekare, T., Detwiler, R.L.: Dissolution of dense non-aqueous phase liquids in vertical fractures: effect of finger residuals and dead-end pools. J. Contam. Hydrol. 149, 88–99 (2013)

    Article  Google Scholar 

  • Zou, L., Jing, L., Cvetkovic, V.: Modeling of solute transport in a 3d rough-walled fracture–matrix system. Transp. Porous Med. 116, 1005–1029 (2017)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Ocean Engineering, IIT-Madras, Chennai, 600036, India

    Renu Valsala

  2. Petroleum Engineering Program, Department of Ocean Engineering, IIT-Madras, Chennai, 600036, India

    Suresh Kumar Govindarajan

Authors
  1. Renu Valsala
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Suresh Kumar Govindarajan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Suresh Kumar Govindarajan.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.

Supplementary material 1 (DOCX 267 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Valsala, R., Govindarajan, S.K. Mathematical Modeling on Mobility and Spreading of BTEX in a Discretely Fractured Aquifer System Under the Coupled Effect of Dissolution, Sorption, and Biodegradation. Transp Porous Med 123, 421–452 (2018). https://doi.org/10.1007/s11242-018-1049-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11242-018-1049-7

Keywords

Search

Navigation