Does modeling framework matter? A comparative study of structural and reduced-form models

Abstract

This study provides a rigorous empirical comparison of structural and reduced-form credit risk frameworks. The literature differentiates between structural models that are based on modeling of the evolution of the balance sheet of the issuer, and reduced-form models that specify credit risk exogenously by a hazard rate process. Until now, there has been no common agreement in academia and practice on which model framework better captures credit risk. As major difference we focus on the discriminative modeling of the default time. In contrast to the previous literature, we calibrate both approaches to the same data set, apply comparable estimation techniques, and assess the out-of-sample prediction quality on the same time series of credit default swap prices. As our empirical implementations of both approaches rely on the same market information we are able to judge whether empirically the model structure itself makes an important difference. Interestingly, our study shows that the models’ prediction power are quite close on average indicating that for pricing purposes the modeling type does not greatly matter compared to the input data used. Still, the reduced-form approach outperforms the structural for investment-grade names and longer maturities. In contrast the structural approach performs better for shorter maturities and sub-investment grade names.

Appendices

Appendix 1: Stochastic intensity model solution

The values for $A(t,T)$, $B(t,T)$, and $C(t,T)$ can be derived as:

$$\begin{aligned}&C(t,T)=\frac{c}{\kappa _l} (1-e^{-\kappa _l(T-t)})\end{aligned}$$

(18)

$$\begin{aligned}&B(t,T) = \Big [e^{-\kappa _r(T-t)}\Big (\frac{c}{\kappa _l \kappa _r}+\frac{c}{\kappa _l(\kappa _l-\kappa _r)}-\frac{1}{\kappa _r}\Big )\Big ]\nonumber \\&\qquad \qquad \qquad +\Big [\frac{b+1}{\kappa _r}-\frac{c}{\kappa _l \kappa _r}-\frac{c}{\kappa _l} \frac{e^{-\kappa _l(T-t)}}{\kappa _l-\kappa _r}\Big ] \end{aligned}$$

(19)

$$\begin{aligned}&A(t,T)=-a(T-t) - \varXi - \varUpsilon + \varGamma + \varLambda - \varPi \end{aligned}$$

(20)

with

$$\begin{aligned} \widetilde{\theta _l}&= \frac{\delta +\frac{\sigma ^2_v}{2}}{\kappa _l}-\nu \end{aligned}$$

(21)

$$\begin{aligned} W&= \frac{c}{\kappa _r\kappa _l}+\frac{c}{\kappa _l(\kappa _l-\kappa _r)} -\frac{b+1}{\kappa _r}\end{aligned}$$

(22)

$$\begin{aligned} Z&= \frac{b+1}{\kappa _r}-\frac{c}{\kappa _l \kappa _r}\end{aligned}$$

(23)

$$\begin{aligned} \varXi&= \widetilde{\theta _l} c \Big [(T-t)-\frac{1-e^{-\kappa _l(T-t)}}{\kappa _l}\Big ]\end{aligned}$$

(24)

$$\begin{aligned} \varUpsilon&= \kappa _r \theta _r \Big [W\frac{1-e^{-\kappa _r(T-t)}}{\kappa _r}+Z(T-t)-\frac{c}{\kappa _l^{2}(\kappa _l-\kappa _r)}\Big (1-e^{-\kappa _l (T-t)}\Big )\Big ]\end{aligned}$$

(25)

$$\begin{aligned} \varGamma&= \frac{\sigma _v^2 c^2}{2\kappa _l^2}\Big [(T-t)-\frac{2(1-e^{-\kappa _l(T-t)})}{\kappa _l}+\frac{1-e^{-2\kappa _l(T-t)}}{2\kappa _l}\Big ]\end{aligned}$$

(26)

$$\begin{aligned} \varLambda&= \frac{\sigma _r^2}{2}\Big [\frac{W^2}{2\kappa _r}(1-e^{-2\kappa _r(T-t)})+\frac{2WZ}{\kappa _r}(1-e^{-\kappa _r(T-t)})+ Z^2(T-t)\nonumber \\&-\frac{2Wc(1-e^{-(\kappa _l+\kappa _r)(T-t)})}{\kappa _l(\kappa _l-\kappa _r)(\kappa _l+\kappa _r)}-\frac{2Zc(1-e^{-\kappa _l(T-t)})}{\kappa _l^2 (\kappa _l-\kappa _r)}\nonumber \\&+ \Big (\frac{c}{\kappa _l(\kappa _l-\kappa _r)}\Big )^2 \frac{1-e^{-2\kappa _l(T-t)}}{2\kappa _l}\Big ]\end{aligned}$$

(27)

$$\begin{aligned} \varPi&= \rho \sigma _v\sigma _r\Big [\frac{Wc(1-e^{-\kappa _r(T-t)})}{\kappa _l\kappa _r}+\frac{Zc(T-t)}{\kappa _l}-\frac{c^2(1-e^{-\kappa _l(T-t)})}{\kappa _l^3(\kappa _l-\kappa _r)}\nonumber \\&-\frac{Wc(1-e^{-(\kappa _l+\kappa _r)(T-t)})}{\kappa _l (\kappa _l+\kappa _r)}-\frac{Zc(1-e^{-\kappa _l(T-t)})}{\kappa _l^2}\nonumber \\&+ \frac{c^2(1-e^{-2\kappa _l(T-t)})}{2\kappa _l^3(\kappa _l-\kappa _r)}\Big ] \end{aligned}$$

(28)

Appendix 2: Structural model solution

Utilizing the framework provided by Longstaff and Schwartz (1995) and Collin-Dufresne and Goldstein (2001), Eom et al. (2004) arrive at the below formulation (pp. 537–539):

$$\begin{aligned} Q^{F_T}(r_0,l_0,T)=\sum _{i=1}^{n} q(t_{i-1/2};t_0) \end{aligned}$$

(29)

In deriving this formula, $t_0$ is set equal to $0$ and the time is discretized into $n$ intervals as $t_i=iT/n$, for $i=1, 2,\ldots , n,$

$$\begin{aligned} q(t_{i-1/2};t_0)=\frac{N(a(t_i;t_0))-\sum _{j=1}^{i-1}q(t_{j-1/2}; t_0)N(b(t_i;t_{j-1/2}))}{N(b(t_i;t_{i-1/2}))} \end{aligned}$$

(30)

The sum on the right hand-side of the equation becomes zero when $i=1$. $N$ is the cdf of Normal distribution. Values for $a$ and $b$ are required to compute $Q^{F_T}(r_0,l_0,T)$ in the structural model. They are given as:

$$\begin{aligned} a(t_i;t_0)&= -\frac{M(t_i,T|X_0,r_0)}{\sqrt{S(t_i|X_{t_j})}}\end{aligned}$$

(31)

$$\begin{aligned} b(t_i;t_j)&= -\frac{M(t_i,T|X_{t_j})}{\sqrt{S(t_i|X_{t_j})}} \end{aligned}$$

(32)

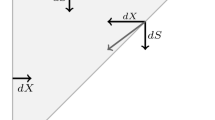
$X=V/K$ is the inverse of the leverage ratio, where $M$ and $S$ are

$$\begin{aligned} M(t,T|X_0,r_0)&= E^{F_T}_0[ln{X_t}]\end{aligned}$$

(33)

$$\begin{aligned} S(t|X_0,r_0)&= var^{F_T}_0[ln{X_t}]\end{aligned}$$

(34)

$$\begin{aligned} M(t,T|X_u)&= M(t,T|X_0,r_0)-M(u,T|X_0,r_0)\frac{cov^{F_T}_0[ln{X_t},ln{X_u}]}{S(u|X_0,r_0)}, u \ \epsilon \ (t_0,t)\nonumber \\\end{aligned}$$

(35)

$$\begin{aligned} S(t|X_u)&= S(t|X_0,r_0)-\frac{(cov^{F_T}_0[ln{X_t},ln{X_u}])^2}{S(u|X_0,r_0)}, \ u \ \epsilon \ (t_0,t) \end{aligned}$$

(36)

What remains is to have closed form solutions for $E^{F_T}_0[ln{X_t}]$ and $cov^{F_T}_0[ln{X_t},ln{X_u}]$ which are computed in Eom/Helwege/Huang (pp. 538–539).

$$\begin{aligned} E^{F_T}_0[ln{X_t}]&= e^{-\kappa _{l}t} \Bigg [ln{X_0}+ \bar{\nu }(e^{\kappa _{l}t}-1)\nonumber \\&+ \Bigg (\frac{1}{\kappa _l-\kappa _r}(e^{(\kappa _l-\kappa _r)t}-1)\Bigg (r_0-\theta _r+\frac{\sigma _r^2}{\kappa _r^2}-\frac{\sigma _r^2}{2\kappa _r^2}e^{-\kappa _{r}T}\Bigg )\nonumber \\&+ \frac{1}{\kappa _l+\kappa _r}\frac{\sigma _r^2}{2\kappa _r^2}e^{-\kappa _{r}T}(e^{(\kappa _l+\kappa _r)t}-1)+\frac{1}{\kappa _l}\Bigg (\theta _r\!-\!\frac{\sigma _r^2}{\kappa _r^2}\Bigg )(e^{\kappa _{l}t}\!-\!1)\!\Bigg )\nonumber \\&- \frac{\rho \sigma _v\sigma _r}{\kappa _r}\Big (\frac{e^{\kappa _{l}t}-1}{\kappa _l}-e^{\kappa _{r}T}\frac{e^{(\kappa _l+\kappa _r)t}-1}{\kappa _l+\kappa _r}\Big )\Bigg ]\nonumber \\ cov^{F_T}_0[ln{X_t},ln{X_u}]&= e^{-\kappa _l(t+u)}\Big [\frac{\sigma _v^2}{2\kappa _l}(e^{2\kappa _{l}u}-1)\nonumber \\&+ \frac{\rho \sigma _v\sigma _r}{\kappa _l+\kappa _r}\Big (\frac{e^{2\kappa _{l}u}-1}{2\kappa _l}-\frac{e^{(\kappa _l-\kappa _r)u}-1}{\kappa _l-\kappa _r}\Big )\nonumber \\&+ \frac{\rho \sigma _v\sigma _r}{\kappa _l+\kappa _r}\Big (\frac{1-e^{(\kappa _l-\kappa _r)t}}{\kappa _l-\kappa _r}+\frac{e^{2\kappa _{l}u}-1}{2\kappa _l}\nonumber \\&+ e^{(\kappa _l+\kappa _r)u}\frac{e^{(\kappa _l-\kappa _r)t}-e^{(\kappa _l-\kappa _r)u}}{\kappa _l-\kappa _r}\Big )\nonumber \\&+ \frac{\sigma _{r}^2}{2\kappa _r}\Big (-\frac{(e^{(\kappa _l-\kappa _r)t}-1)(e^{(\kappa _l-\kappa _r)u}-1)}{(\kappa _l-\kappa _r)^2}\nonumber \\&-\frac{\kappa _r}{\kappa _l^2-\kappa _r^2}\frac{e^{2\kappa _{l}u}-1}{\kappa _l}+(e^{(\kappa _l+\kappa _r)u}-1)\frac{e^{(\kappa _l-\kappa _r)t}-e^{(\kappa _l-\kappa _r)u}}{\kappa _{l}^2-\kappa _{r}^2}\nonumber \\&+\frac{1}{\kappa _l^2-\kappa _r^2}(1-2e^{(\kappa _l-\kappa _r)u}+e^{2\kappa _{l}u})\Big )\Bigg ] \end{aligned}$$

(37)

where

$$\begin{aligned} \bar{\nu }=(\nu - (\delta + \sigma _v^2/2)/ \kappa _l) \end{aligned}$$

(38)

From these equations one can obtain $Q^{F_T}(r_0,l_0,T)$ required for pricing the bond.

Appendix 3: List of bonds used in analysis

See Table 13

Table 13 List of bonds used in analysis

Appendix 4: Estimation results

See Tables 14, 15, 16

Table 14 Structural model estimation figures

Table 15 Intensity model parameter estimates

Table 16 Model-implied and actual probabilities of default

Appendix 5: Simulation algorithm

For the structural model, paths of the short rate and the leverage ratio are simulated where default occurred at the first time when the log-leverage is larger than zero (leverage is greater than or equal to 1). For a typical 5-year horizon of the maturity of the CDS, the simulation algorithm generates paths and at each time point the log-leverage is checked for whether it has a value higher than zero:

• (i) At first step, the short rate is simulated using an Euler discretization of the Vasicek process: Start with $r_{t}=r_0$, and generate $r_{t+1}$ through

  $$\begin{aligned} r_{t+1}=r_t+ \kappa _r(\theta _r-r_t)\Delta t + \sigma _r \sqrt{\Delta t} \epsilon ^1_t \end{aligned}$$

  (39)

  where $\epsilon ^1_t \sim N(0,1)$.

• (ii) Substitute the simulated $r_{t+1}$ into

  $$\begin{aligned} \theta _l(r_{t+1})=-\bar{\nu }-\frac{r_{t+1}}{\kappa _l} \end{aligned}$$

  (40)

• (iii) Generate $l_{t+1}$ through Euler discretization of the leverage process:

  $$\begin{aligned} l_{t+1}=l_t+ \kappa _l(\theta _l-l_t)\Delta t- \sigma _v \sqrt{\Delta t}(\rho \epsilon ^1_t+\sqrt{1-\rho ^2}\epsilon ^2_t) \end{aligned}$$

  (41)

  Here, note that the Brownian motions of the two processes are correlated with a factor of $\rho$ and $\epsilon ^2_t \sim N(0,1)$.

  • a. If $l_{t+1} < 0$ (log leverage having a negative sign) then no default occurs. The CDS premiums up to this time point are cumulated, when a quarter is complete (typical quarterly payments is assumed). This accumulation constitutes the “Premium Leg” of a CDS.

    $$\begin{aligned} PremLeg_{i} = PremLeg_{i-1} + \Big ( e^{- \sum \limits _{0}^{t_i} r_{t_i} \Delta t}\Big ) \end{aligned}$$

    (42)

    Here, $t_i$ is the ith premium date. Simulation continues with step (iv).

  • b. If $l_{t+1} \ge 0$, default happens. Simulation is terminated and the recovery leg is computed to constitute the numerator of the fair price of a CDS. $\tau =t+1$ and

    $$\begin{aligned} RecLeg = \Big ( e^{- \sum \limits _{0}^\tau r_{t} \Delta t} (1- \varphi \cdot b(r_{\tau },T-\tau ))\Big ) \end{aligned}$$

    (43)

    In addition, the accrued premium since the last premium payment is calculated and added to the premium leg. In this implementation, the recovered bond maturity $(T)$ is taken to be the longest dated bond’s maturity. According to the intuition, with no recovery on coupons, the longest available bond should be delivered in case the “cheapest-to-deliver” option is available.

• (iv) Go back to step (i) to generate $r_{t+2}$.

For simulating the fair price of a CDS in the reduced-form case, Euler discretizations for the short rate and leverage process as in Eqs. (39) and (41) have been used. Following Schönbucher (2003), a uniform random variate $U$ is generated as the trigger level. Let $\gamma$ be the default countdown process, which is initiated by letting $\gamma (0)=1$. Different from the structural model described above, step (iii) is replaced by:

• (iii) Generate $l_{t+1}$ through Euler discretization of the leverage process:

  $$\begin{aligned} l_{t+1}=l_t+ \kappa _l(\theta _l-l_t)\Delta t- \sigma _v \sqrt{\Delta t}(\rho \epsilon ^1_t+\sqrt{1-\rho ^2}\epsilon ^2_t) \end{aligned}$$

  (44)

  Compute the associated default intensity as:

  $$\begin{aligned} \lambda (t+1)=a+cl_{t+1} \end{aligned}$$

  (45)

  Then at each time step, the default countdown process is decreased by,

  $$\begin{aligned} \gamma (t+1)=\gamma (t)e^{\lambda (t+1)\Delta t} \end{aligned}$$

  (46)

• a. If $U < \gamma (t+1)$ then no default occurs. Similar to the structural side, the CDS premiums up to this quarter are cumulated, when a quarter is complete. This is the premium leg of the CDS.

  $$\begin{aligned} PremLeg_{i} = PremLeg_{i-1} + \Big ( e^{- \sum \limits _{0}^{t_i} r_{t_i} \Delta t}\Big ) \end{aligned}$$

  (47)

• b. If $U \ge \gamma (t+1)$, default happens and the recovery leg is computed.

  $$\begin{aligned} RecLeg = \Big ( e^{- \sum \limits _{0}^\tau r_{t} \Delta t} (1- \varphi \cdot b(r_{\tau },T-\tau ))\Big ) \end{aligned}$$

  (48)

  Accrued premiums are taken into account since the last premium payment date, as well.