Skip to main content
SpringerLink
Log in

Developers, Herding, and Overbuilding

  • Published:
The Journal of Real Estate Finance and Economics Aims and scope Submit manuscript

Abstract

Recent years have seen the most pronounced turbulence that real estate markets have ever experienced. There have been wild swings in prices, a wave of foreclosures, countless failed investments, and massive overbuilding. This paper will be primarily concerned with overbuilding. Of the many forces that may have combined to produce this situation, the paper will focus on rational overbuilding carried out by developers whose decisions are made under uncertainty. We will establish the possibility of both statistical and reputation-based herding. The former refers to developers learning from each other, and so tending to copy. The latter refers to developers copying each other in order to reduce the probability of a loss of reputation that can result from making an unconventional choice.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. This decline does not reflect an increase in sales, which were 52% lower in January 2010 than in January 2008. The increase in inventories instead reflects a severe decline in construction.

  2. The seasonally adjusted index peaked in May 2006; the non-seasonally adjusted 20 city composite index peaked in July 2006. The January 2008 inventory peak represented a 147% increase over the July 2006 value.

  3. The housing data above is all from the U.S. Census Bureau, except the “months supply of existing homes”, which comes from a National Association of Realtors news release, February 26, 2010.

  4. The “New Houses Under Construction” plotted in Fig. 1 is an Index created by the authors, with January 2005=100.

  5. New home sales were 102,000 in May 2006, and 68,000 in July 2007. Source: U.S. Census Bureau.

  6. Since some markets experience much more pronounced cycles than others (Ghent and Owyang 2010), it is likely that the national average data understate the extent of overbuilding in some highly volatile markets.

  7. See Grenadier (1996) for an interesting and very different analysis of overbuilding that also makes no assumption of irrationality. His explanation is quite different, as we will make clear below.

  8. Wang and Zho (2000) present a quite different analysis from ours, where, in a two-stage model, overbuilding arises in a game of excess entry. In their model, quantity competition occurs first, and price competition comes second. The latter is assumed to involve collusion, which means that prices do not fall in order to eliminate the surplus. The former is assumed to not involve collusion, giving rise to the excess entry/overbuilding.

  9. See the Appendix for details.

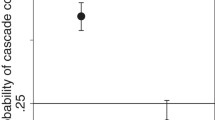
  10. The analysis here has been laid out to establish the possibility of a cascade in one particular market. There is nothing in the model that prevents cascades from taking place in different markets simultaneously.

  11. The differences between these markets were profound. In the fourth quarter of 2005, the FHFA MSA House Price Index for Phoenix rose at an annual rate of 40.87% (www.fhfa.gov). The previous three quarters had brought annual increases in the HPI of 21.84%, 31.67%, and 35.95%. In Fargo, the increases for the four quarters of 2005 were 7.28%, 8.93%, 6.71%, and 5.63%.

  12. The signal si is an element of the continuous set of possible locations. This contrasts with the high-state or low-state signal σ i from the last section.

  13. This assumption ensures that the bank’s rule for future project funding depends only on its posterior estimate of the probability that a developer is good.

  14. In this case, a perfect Bayesian equilibrium requires that the developer choose a location that is optimal given the developer’s own signal, the congestion associated with other developers’ location choices, the signals that can be inferred from other developers’ location choices, and the bank’s updating and funding rules. In addition, the bank must update according to Bayes Rule given the developer’s equilibrium strategies. This means that bank beliefs must be consistent with optimal developer strategies.

  15. The location signal is, of course, a metaphor for a developer’s judgment as to the most promising development location. From a practical perspective, a developer would never select an alternative location unless choosing to copy the choice of another developer, with the latter providing some evidence the location might be good and the protection of the “herd”. In particular, randomly selecting a location would not only assure failure within the model, but would, in practice, not be a sensible choice for a developer.

  16. The posterior is the probability that the developer is good conditional on failing. This equals the probability of failing conditional on being good, (1−α), multiplied by the unconditional probability of being good, p, divided by the unconditional probability of failing (1−αp).

  17. The off-the-equilibrium path beliefs need not be consistent with equilibrium play. If the bank believed that developer 2 was bad with probability 1 whenever a2 ≠ a1, then there would be even stronger reason for developer 2 to herd. This highly punitive off-the-equilibrium path belief is also consistent with equilibrium.

  18. We have chosen the model to make some complex reputational issues as simple as possible. Proposition 2 should not be interpreted literally as suggesting that all development will take place in one location. Instead, the analysis suggests the existence of a reputational force that encourages conformity. Thus, the model here, as with the cascades model analyzed previously, is consistent with herding leading to overbuilding in many markets (i.e., Tampa and Phoenix).

  19. See the Appendix for the details of the updating.

  20. We are continuing with the two-developer, sequential choice framework to avoid confusion. However, it is trivial to alter the model to consider one fully-informed developer choosing whether to join in an ongoing episode of overbuilding at some boom location, or selecting her signaled location which is good with probability 1.

  21. In this specification, the bank is not involved in the initial round of development. Its only role is to offer funding for future projects, and thus make reputation matter.

References

  • Aizenman, J., & Jinjarak, Y. (2009). Current account patterns and national real estate markets. Journal of Urban Economics, 66(2), 75–89.

    Article  Google Scholar 

  • Banerjee, A. V. (1992). A simple model of herd behavior. Quarterly Journal of Economics, 107(3), 797–818.

    Article  Google Scholar 

  • Berliant, M., & Kung, F.-C. (2010). Can information asymmetry cause agglomeration? Regional Science and Urban Economics, 40(4), 196–209.

    Article  Google Scholar 

  • Bikchandani, S., Hirshleifer, D., & Welch, I. (1992). A theory of fads, fashion, custom, and cultural change as informational cascades. Journal of Political Economy, 100(5), 992–1026.

    Article  Google Scholar 

  • Bikchandani, S., Hirshleifer, D., & Welch, I. (1998). Learning from the behavior of others: conformity, fads, and informational cascades. The Journal of Economic Perspectives, 12(3), 151–170.

    Article  Google Scholar 

  • Bikhchandani, S., & Sharma, S. (2000). Herd behavior in financial markets: a review. IMF Working Paper.

  • Case, K., & Shiller, R. (2003). Is there a bubble in the housing market. Brookings Papers on Economic Activity, 2, 299–362.

    Article  Google Scholar 

  • Chamley, C. (2004). Rational herds: Economic models of social learning. Cambridge: Cambridge University Press.

    Google Scholar 

  • Cipriani, M., & Guarino, A. (2008). Herd behavior and contagion in financial markets. The B.E. Journal of Theoretical Economics, 8(1), Article 24.

  • Cresswell, J. (2005). Home builders’ stock sales: Diversifying or bailing out? New York Times, October 4, p. C1.

  • Dasgupta, A., & Prat, A. (2006). Financial equilibrium with career concerns. Theoretical Economics, 1(1), 67–93.

    Google Scholar 

  • Dasgupta, A., & Prat, A. (2008). Information aggregation in financial markets with career concerns. Journal of Economic Theory, 143(1), 83–113.

    Article  Google Scholar 

  • DeCoster, G., & Strange, W. (1993). Spurious agglomeration. Journal of Urban Economics, 33(3), 273–304.

    Article  Google Scholar 

  • Duranton, G., & Puga, D. (2004). Micro-foundations of urban agglomeration economies. In J. V. Henderson & J.-F. Thisse (Eds.), Handbook of urban and regional economics (Vol. 4, pp. 2063–2118). North Holland: Elsevier.

    Google Scholar 

  • Economist. (2007). The rise and fall of the shopping mall. December 18, 2007.

  • Effinger, M. R., & Polborn, M. K. (2001). Herding and anti-herding: a model of reputational differentiation. European Economic Review, 45(3), 385–403.

    Article  Google Scholar 

  • Eid, J., Overman, H. G., Puga, D., & Turner, M. A. (2008). Fat city: questioning the relationship between urban sprawl and obesity. Journal of Urban Economics, 63(2), 385–404.

    Article  Google Scholar 

  • Ewing, R., Schmid, T., Killingsworth, R., Zlot, A., & Raudenbush, S. (2003). Relationship between urban sprawl and physical activity and morbidity. American Journal of Health Promotion, 18(1), 47–57.

    Article  Google Scholar 

  • Ferreira, F., Gyourko, G., & Tracy, J. (2010). Housing busts and household mobility. Journal of Urban Economics, 68(1), 34–45.

    Article  Google Scholar 

  • Foote, C. L., Gerardi, K., & Willan, P. S. (2008). Negative equity and foreclosure: theory and evidence. Journal of Urban Economics, 64(2), 234–245.

    Article  Google Scholar 

  • Fujita, M., & Thisse, J. (2002). The economics of agglomeration. Cambridge: Cambridge University Press.

    Google Scholar 

  • Garreau, J. (1992). Edge city: Life on the new frontier. Toronto: Anchor.

    Google Scholar 

  • Ghent, A. C., & Owyang, M. T. (2010). Is housing the business cycle? Evidence from U.S. cities. Journal of Urban Economics, 67(3), 336–351.

    Article  Google Scholar 

  • Glaeser, E. L., Gyourko, J., & Saiz, A. (2008). Housing supply and housing bubbles. Journal of Urban Economics, 64(2), 198–217.

    Article  Google Scholar 

  • Grenadier, S. R. (1996). The strategic exercise of options: development cascades and overbuilding in real estate markets. The Journal of Finance, 51(5), 1653–1679.

    Article  Google Scholar 

  • Haughwout, A., Peach, R., & Tracy, J. (2008). Juvenile delinquent mortgages: bad credit or bad economy. Journal of Urban Economics, 64(2), 246–257.

    Article  Google Scholar 

  • Hirshleifer, D., & Teoh, S. (2003). Herd behavior and cascading in capital markets: a review and synthesis. European Financial Management, 9(1), 25–66.

    Article  Google Scholar 

  • Keynes, J. M. (1936). The general theory of employment, interest, and money. New York: Harcourt, Brace, & World.

    Google Scholar 

  • Lee, S., & Somerville, T. (2009). Lemons in real estate: Do people believe repairs? Working paper.

  • Pascal, A. H., & McCall, J. J. (1980). Agglomeration economies and search costs. Journal of Urban Economics, 8(3), 383–388.

    Article  Google Scholar 

  • Rosenthal, S. S., & Strange, W. C. (2004). Evidence on the nature and sources of agglomeration economies. In J. V. Henderson & J.-F. Thisse (Eds.), Handbook of urban and regional economics, vol 4 (pp. 2119–2172). Amsterdam: Elsevier.

    Google Scholar 

  • Rybczynski, W. (2008). Last harvest: How a cornfield became New Daleville: Real estate development in America. New York: Scribner.

    Google Scholar 

  • Scharfstein, D., & Stein, J. (1990). Herd behavior and investment. American Economic Review 83, 465–479.

    Google Scholar 

  • Shafran, A. (2008). Risk externalities and the problem of wildfire risk. Journal of Urban Economics, 64(2), 488–495.

    Article  Google Scholar 

  • Strange, W., Hejazi, W., & Tang, J. (2006). The uncertain city: competitive instability, skills, innovation, and the strategy of agglomeration. Journal of Urban Economics, 59(3), 331–351.

    Article  Google Scholar 

  • Wang, K., & Zho, Y. (2000). Overbuilding: a game-theoretic approach. Real Estate Economics, 28(3), 493–522.

    Article  Google Scholar 

  • Welch, I. (1992). Sequential sales, learning, and cascades. Journal of Finance, 47(2), 695–732.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Economics, Bowdoin College, Brunswick, ME, 04011-8497, USA

    Gregory P. DeCoster

  2. Rotman School of Management, University of Toronto, 105 St. George Street, Toronto, ON, M5S 3E6, Canada

    William C. Strange

Authors
  1. Gregory P. DeCoster
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. William C. Strange
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to William C. Strange.

Additional information

We gratefully acknowledge the financial support of the Social Sciences and Humanities Research Council of Canada and the Desautels Centre for Integrative Thinking. We are also grateful for the helpful suggestions of an anonymous referee, Jan Brueckner, Paul Calem, Mark Shroder, Stacy Sirmans, and the participants of the Florida State University Symposium on The Economics of Information in Real Estate Markets. For excellent research assistance, we thank John Shennan and Elizabeth Weston.

Appendix

Appendix

This Appendix contains additional detail on the Bayesian updating of developer quality.

Section III

The expected profit for the first developer choosing “build” is \( {\text{E}}\left( {\left. {\text{V}} \right|\sigma = {\sigma^{\text{H}}}} \right) - {\text{F}} - {\text{C}} \) if the developer receives the high state signal. Since revenues are either VH or 0, \( {\text{E}}\left( {\left. {\text{V}} \right|\sigma = {\sigma^{\text{H}}}} \right) = {\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|\sigma = {\sigma^{\text{H}}}} \right){{\text{V}}^{\text{H}}} \). By Bayes Rule, \( {\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|\sigma = {\sigma^{\text{H}}}} \right) = {\text{prob}}\left( {\sigma = \left. {{\sigma^{\text{H}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right){\text{prob}}\left( {\sigma = {\sigma^{\text{H}}}} \right)/{\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}}} \right) \). By assumption, prob(V = VH)    =  1/2. The unconditional probability of receiving the good signal is \( {\text{prob}}\left( {\sigma = {\sigma^{\text{H}}}} \right) = {\text{prob}}\left( {\sigma = \left. {{\sigma^{\text{H}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right){\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}}} \right) + {\text{prob}}\left( {\sigma = \left. {{\sigma^{\text{H}}}} \right|{\text{V}} = 0} \right){\text{prob}}\left( {{\text{V}} = 0} \right) = \phi * \left( {{1}/{2}} \right) + \left( {{1} - \phi } \right) * \left( {{1}/{2}} \right) = {1}/{2} \). Thus, \( {\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|\sigma = {\sigma^{\text{H}}}} \right) = \phi \), so we have \( {\text{E}}\left( {\left. {\text{V}} \right|\sigma = {\sigma^{\text{H}}}} \right) = \phi {{\text{V}}^{\text{H}}} - {\text{F}} - {\text{C}}. \)

Suppose that the first developer has behaved as if she has received the high state signal. If the second developer receives the high signal, then we have by Bayes’ Rule

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}}} \right) = {\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = \left. {{\sigma^{\text{H}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right)} \hfill \\ {\quad \quad \quad * {\text{ prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}}} \right)/{\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}}} \right)} \hfill \\ {\quad \quad \quad = {\phi^{{2}}} * \left( {{1}/{2}} \right)/\left[ {\left( {{1}/{2}} \right)\left[ {{\phi^{{2}}} + {{\left( {{1} - \phi } \right)}^{{2}}}} \right]} \right] = {\phi^{{2}}}/\left[ {{\phi^{{2}}} + {{\left( {{1} - \phi } \right)}^{{2}}}} \right]} \hfill \\ \end{array} $$
(A.1)

If the second developer receives the low signal, we have

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{L}}}} \right) = {\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = \left. {{\sigma^{\text{L}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right)} \hfill \\ {\quad \quad \quad * {\text{ prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}}} \right)/{\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = \phi * \left( {{1} - \phi } \right) * \left( {{1}/{2}} \right)/\left[ {\phi * \left( {{1} - \phi } \right)} \right] = {1}/{2}} \hfill \\ \end{array} $$
(A.2)

If the third developer observes that both predecessors have built but obtains a negative signal, the probability of the high state is by Bayes’ Rule equal to:

$$ \begin{array}{*{20}c} {{{\text{prob}}{\left( {{\text{V}} = {\text{V}}^{{\text{H}}} \left| {\sigma _{1} = } \right.\sigma ^{{\text{H}}} \cap \sigma _{2} = \sigma ^{{\text{H}}} \cap \sigma _{3} = \sigma ^{{\text{L}}} } \right)}}} \hfill \\ {\quad \quad \quad \quad { = {\text{prob}}{\left( {\sigma _{1} = \sigma ^{{\text{H}}} \cap \sigma _{2} = \sigma ^{{\text{H}}} \cap \sigma _{3} = \sigma ^{{\text{L}}} \left| {{\text{V}} = {\text{V}}^{{\text{H}}} } \right.} \right)}}} \hfill \\ {\quad \quad \quad \quad {*{\text{prob}}{\left( {{\text{V}} = {\text{V}}^{{\text{H}}} } \right)}/{\text{prob}}{\left( {\sigma _{1} = \sigma ^{{\text{H}}} \cap \sigma _{2} = \sigma ^{{\text{H}}} \cap \sigma _{3} = \sigma ^{{\text{L}}} } \right)}}}\hfill \\ {\quad \quad \quad \quad { = \phi ^{2} *{\left( {1 - \phi } \right)}*{\left( {1/2} \right)}/{\left( {1/2} \right)}{\left[ {\phi ^{2} {\left( {1 - \phi } \right)} + {\left( {1 - \phi } \right)}^{2} \phi } \right]}}} \hfill \\ {\quad \quad \quad \quad { = \phi ^{2} {\left( {1 - \phi } \right)}/{\left[ {\phi ^{2} {\left( {1 - \phi } \right)} + {\left( {1 - \phi } \right)}^{2} \phi } \right]} = \phi .}} \hfill \\ \end{array} $$
(A.3)

In the case where developers differ in quality, the probability of a high state of nature when developers 1 and 2 have received positive signals and developer 3 has received a negative signal is

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {{\text{V}} = \left. {{{\text{V}}^{\text{H}}}} \right|{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}} \cap {\sigma_{{3}}} = {\sigma^{\text{L}}}} \right) = {\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}} \cap {\sigma_{{3}}} = \left. {{\sigma^{\text{L}}}} \right|{\text{V}} = {{\text{V}}^{\text{H}}}} \right)} \hfill \\ {\quad \quad \quad * {\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}}} \right)/{\text{prob}}\left( {{\sigma_{{1}}} = {\sigma^{\text{H}}} \cap {\sigma_{{2}}} = {\sigma^{\text{H}}} \cap {\sigma_{{3}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = \left[ {{\phi_{{1}}}{\phi_{{2}}}\left( {{1} - {\phi_{{3}}}} \right)} \right]/\left[ {{\phi_{{1}}}{\phi_{{2}}}\left( {{1} - {\phi_{{3}}}} \right) + \left( {{1} - {\phi_{{1}}}} \right)\left( {{1} - {\phi_{{2}}}} \right){\phi_{{3}}}} \right].} \hfill \\ \end{array} $$
(A.4)

Section IV

In this section, we have assumed that there are multiple good locations. This means that updating will be based only on whether projects succeed or fail when the developers have picked different locations. If the second developer selects a distinct location and succeeds, the probability of the developer being good is

$$ \begin{array}{*{20}c} {{{\text{prob}}{\left( {{\text{developer}}\;2\;{\text{is}}\;{\text{good}}\left| {{\text{developer}}\;2\;{\text{succeeds}}} \right.} \right)}}} \hfill \\ {\quad \quad \quad { = {\text{prob}}{\left( {{\text{developer}}\;2\;{\text{succeeds}}\left| {{\text{developer}}\;2\;{\text{is}}\;{\text{good}}} \right.} \right)}}} \hfill \\ {\quad \quad \quad {*{\text{prob}}{\left( {{\text{developer}}\;2\;{\text{is}}\;{\text{good}}} \right)}/{\text{prob}}{\left( {{\text{developer}}\;2\;{\text{succeeds}}} \right)}}} \hfill \\ {\quad \quad \quad { = \alpha *{\text{p}}/{\left[ {{\text{p}}\alpha + {\left( {1 - {\text{p}}} \right)}\beta } \right]} > {\text{p}}}} \hfill \\ \end{array} $$
(A.5)

If the second developer selects a distinct location and fails, the probability of the developer being good is

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {\left. {\text{developer 2 is good}} \right|{\text{developer 2 fails}}} \right)} \hfill \\ {\quad \quad \quad = {\text{prob}}\left( {\left. {\text{developer 2 fails}} \right|{\text{developer 2 is good}}} \right)} \hfill \\ {\quad \quad \quad * {\text{prob}}\left( {\text{developer 2 is good}} \right)/{\text{prob}}\left( {\text{developer 2 fails}} \right)} \hfill \\ {\quad \quad \quad = \left( {{1} - \alpha } \right){\text{p}}/\left[ {{\text{p}}\left( {{1} - \alpha } \right) + \left( {{1} - {\text{p}}} \right)\left( {{1} - \beta } \right)} \right] < {\text{p}}.} \hfill \\ \end{array} $$
(A.6)

Section V

Suppose that the high state of nature is realized. If developer 3 chooses “elsewhere” and developers 1 and 2 both choose build, then the bank’s posterior estimate of developer 3’s quality is:

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {\left. {\text{developer 3 is good}} \right|{\text{V}} = {{\text{V}}^{\text{H}}} \cap {\sigma_{{3}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = {\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}} \cap {\sigma_{{3}}} = \left. {{\sigma^{\text{L}}}} \right|{\text{developer 3 is good}}} \right)} \hfill \\ {\quad \quad \quad * {\text{prob}}\left( {\text{developer 3 is good}} \right)/{\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{H}}} \cap {\sigma_{{3}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = {\text{p}}\left( {{1} - \phi } \right) * \left( {{1}/{2}} \right)/\left[ {\left( {{1}/{2}} \right)\left[ {{\text{p}}\left( {{1} - \phi } \right) + \left( {{1} - {\text{p}}} \right)\left( {{1}/{2}} \right)} \right]} \right] = {\text{p}}\left( {{1} - \phi } \right)/\left[ {{\text{p}}\left( {{1} - \phi } \right) + \left( {{1} - {\text{p}}} \right)\left( {{1}/{2}} \right)} \right] < {\text{p}}} \hfill \\ \end{array} $$
(A.7)

Similarly, if developers 1 and 2 both choose build and the low state of nature is realized, and developer 3 has received the low-state signal, the bank’s posterior for developer 3 is:

$$ \begin{array}{*{20}{c}} {{\text{prob}}\left( {\left. {\text{developer 3 is good}} \right|{\text{V}} = {{\text{V}}^{\text{L}}} \cap {\sigma_{{3}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = {\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{L}}} \cap {\sigma_{{3}}} = \left. {{\sigma^{\text{L}}}} \right|{\text{developer 3 is good}}} \right)} \hfill \\ {\quad \quad \quad * {\text{prob}}\left( {\text{developer 3 is good}} \right)/{\text{prob}}\left( {{\text{V}} = {{\text{V}}^{\text{L}}} \cap {\sigma_{{1}}} = {\sigma^{\text{L}}}} \right)} \hfill \\ {\quad \quad \quad = {\text{p}}\phi * \left( {{1}/{2}} \right)/\left[ {\left( {{1}/{2}} \right) \left[ {{\text{p}}\phi + \left( {{1} - {\text{p}}} \right)\left( {{1}/{2}} \right)} \right]} \right] = {\text{p}}\phi /\left[ {{\text{p}}\phi + \left( {{1} - {\text{p}}} \right)\left( {{1}/{2}} \right)} \right] > {\text{p}}.} \hfill \\ \end{array} $$
(A.8)

Rights and permissions

Reprints and permissions

About this article

Cite this article

DeCoster, G.P., Strange, W.C. Developers, Herding, and Overbuilding. J Real Estate Finan Econ 44, 7–35 (2012). https://doi.org/10.1007/s11146-011-9309-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11146-011-9309-0

Keywords

JEL Codes

Search

Navigation