Noise effects on entanglement distribution by separable state

Abstract

We investigate noise effects on the performance of entanglement distribution by separable state. We consider a realistic situation in which the mediating particle between two distant nodes of the network goes through a noisy channel. For a large class of noise models, we show that the average value of distributed entanglement between two parties is equal to entanglement between particular bipartite partitions of target qubits and exchange qubit in intermediate steps of the protocol. This result is valid for distributing two-qubit/qudit and three-qubit entangled states. In explicit examples of the noise family, we show that there exists a critical value of noise parameter beyond which distribution of distillable entanglement is not possible. Furthermore, we determine how this critical value increases in terms of Hilbert space dimension, when distributing d-dimensional Bell states.

Appendices

Appendix A: Concurrence

Concurrence which is a measure for quantifying entanglement in a two-qubit system describing by density matrix $\rho$ is defined as follows [29]:

$$\begin{aligned} C(\rho )=\max \lbrace 0,\lambda _{1}-\lambda _{2}-\lambda _{3}-\lambda _{4}\rbrace ,\quad \lambda _{1}\ge \lambda _{2}\ge \lambda _{3}\ge \lambda _{4}, \end{aligned}$$

(A1)

where $\lambda _{i}$ sorting in decreasing order are square root of eigenvalues of matrix $\rho \tilde{\rho }$ where $\tilde{\rho }$ is defined as:

$$\begin{aligned} \tilde{\rho }=(\sigma _{y}\otimes \sigma _{y})\rho ^{*}(\sigma _{y}\otimes \sigma _{y}), \end{aligned}$$

(A2)

in which $\rho ^{*}$ is the complex conjugate of $\rho$ in computational basis: $\{ \vert 00\rangle$, $\vert 01\rangle$, $\vert 10\rangle , \vert 11\rangle \}$ and $\sigma _y$ is the Pauli matrix: $\sigma _y=-~i(|0\rangle \langle 1|-|1\rangle \langle 0|)$.

Appendix B: Negativity

Negativity is an entanglement measure which is based on an partial transposition criterion for separability [34]. For a bipartite system describing by density matrix $\rho \in \mathcal {H}_A\otimes \mathcal {H_{B}}$, it is defined as follows [33]:

$$\begin{aligned} N(\rho )=\frac{\Vert \rho ^{T_{A}}\Vert _{1}-1}{d-1}, \end{aligned}$$

(B1)

where $\rho ^{T_{A}}$ is partial transpose of density matrix $\rho$ with respect to partition A, $d=\hbox {min}\{\hbox {dim}\mathcal {H}_A,\hbox {dim}\mathcal {H}_B\}$ and $\Vert X \Vert =tr\sqrt{X^{\dag }X}$ is the trace norm. Denoting the eigenvalues of $\rho ^{T_A}$ by $\lambda _i$s, negativity is given by

$$\begin{aligned} N(\rho )=\frac{\left( \sum _{i}|\lambda _{i}|\right) -1}{d-1}, \end{aligned}$$

(B2)

It is easy to see that negativity can be written in terms of negative eigenvalues of $\rho ^{T_A}$ as follows:

$$\begin{aligned} N(\rho )=\frac{2\sum _i'|\lambda _i|}{d-1}. \end{aligned}$$

(B3)

where the summation $\sum _i'$ is over negative eigenvalues of $\rho ^{T_A}$.

Appendix C: Noise effects on distributing two qudit entangled states

In this appendix we analyse the effect of noise on distributing entanglement between two qudits. We consider two types of noise: depolarizing channel and amplitude damping channel.

1.1 1. Depolarizing channel

In Sect. 4.1 by analysing the effect of depolarizing channel on EDSS protocol for distributing entanglement between two qubits, we showed that there is a critical value of noise parameter, beyond which entanglement distribution is impossible. It naturally raises some question like how this critical value may depend on dimension of system and whether or not in higher dimensions the protocol performs as well as it does in two-dimensional case. To answer these questions, we start our analysis by considering a separable initial state which is shown to be suitable for distributing d-dimensional Bell states between Alice and Bob in ideal case [24]:

$$\begin{aligned} \Omega ^{(0)}_{abc}= & {} \frac{d}{D(2d-1)}\sum _{k=0}^{D-1}\vert \phi (k),\phi (-k),0\rangle \langle \phi (k),\phi (-k),0\vert \nonumber \\&+\frac{1}{d(2d-1)}\sum _{j\ne l}\Pi _{jj,l-j}, \end{aligned}$$

(C1)

where

$$\begin{aligned} \vert \phi (\pm k)\rangle =\frac{1}{\sqrt{d}}\sum _{j=0}^{d-1}w^{\pm s_{j}k}\vert j\rangle ,\quad k=0,1,\ldots ,D-1, \end{aligned}$$

with $w=e^{\frac{2\pi i}{D}}$, $D=2^{d}-1$ and $s_{i}=2^{i}-1$. Alice generates entanglement between a and bc by performing CNOT gate on qudits a and c which are initially in her laboratory:

$$\begin{aligned} \Omega ^{(1)}_{abc}= & {} C_{ac}\left( \Omega ^{(0)}_{abc}\right) \nonumber \\= & {} \frac{1}{2d-1}\vert \mathrm {GHZ_3^{(d)}}\rangle \langle \mathrm {GHZ}_3^{(d)}\vert +\frac{1}{d(2d-1)}\sum _{j\ne l}(\Pi _{jjl}+\Pi _{jlj}),\nonumber \\ \end{aligned}$$

(C2)

Exchange qudit c, through which qudits a and b interact, is sent to Bob through a depolarizing channel which is defined as follows:

$$\begin{aligned} \mathcal {E}(X)=(1-p)X+\frac{p}{d} tr(X)\mathrm {I_d}, \end{aligned}$$

(C3)

where $\mathrm {I}_d$ is d-dimensional identity operator. After sending qudit c through the noisy channel to Bob, the state of the all three qudits is described by:

$$\begin{aligned} \Omega ^{(1)'}_{abc}= & {} \mathcal {E}\left( \Omega ^{(1)}_{abc}\right) =(1-p)\Omega ^{(1)}_{abc}\nonumber \\&+\frac{p}{d^2(2d-1)}\left( d\sum _{j=0}^{d-1}\Pi _{jj}+\sum _{i\ne j}\Pi _{ij}\right) \otimes \mathrm {I}_d. \end{aligned}$$

(C4)

In the next step Bob performs inverse CNOT gate on qudits b and c which gives

$$\begin{aligned} \Omega ^{(2)'}_{abc}= & {} C^{-1}_{bc}\left( \Omega ^{(1)'}_{ abc}\right) =(1-p)\Omega ^{(2)}_{abc}\nonumber \\&+\frac{p}{d^{2}(2d-1)}\left( (d-1)\sum _{j,k=0}^{d-1}\Pi _{j,j,k-j}+\sum _{ j, k,l=0}^{d-1}\Pi _{j,l,k-l}\right) , \end{aligned}$$

(C5)

with

$$\begin{aligned} \Omega ^{(2)}_{abc}= & {} \frac{1}{2d-1}\vert \chi _{0}\rangle \langle \chi _{0}\vert \otimes \vert 0\rangle \langle 0\vert \nonumber \\&+\frac{1}{d(2d-1)}\sum _{j\ne l}(\Pi _{j,l,j-l}+\Pi _{j,j,l-j}). \end{aligned}$$

(C6)

where $\vert \chi _{0}\rangle =\frac{1}{\sqrt{d}}\sum _{j=0}^{d-1}\vert jj\rangle$ is d-dimensional maximally entangled state. When Bob measures ancilla in computational basis, the state of qudits a and b is projected to separable state for any outcome of measurement by except $|0\rangle$. If the outcome of the measurement is $|0\rangle$, state of qudits a and b is projected to an entangled state $\Omega _{ab}^{(0)}$:

$$\begin{aligned} \Omega _{ab}^{(0)}=\frac{1}{d+p(d-1)}\left( d(1-p)\vert \chi _{0}\rangle \langle \chi _{0}\vert +p\sum _{j=0}^{d-1}\Pi _{jj}+\frac{p}{d}\sum _{j\ne l}\Pi _{jl}\right) , \end{aligned}$$

(C7)

Hence, success probability of protocol in distributing entanglement between a and b is equal to the probability of having outcome $|0\rangle$ in measuring qudit c and is given by probability:

$$\begin{aligned} p_s=\frac{d+p(d-1)}{d(2d-1)}. \end{aligned}$$

(C8)

Quantifying the entanglement properties of $\Omega _{ab}^{(0)}$ by negativity, we find that there is a critical value of noise probability

$$\begin{aligned} p_{c}=\frac{d}{d+1}, \end{aligned}$$

(C9)

beyond which negativity is equal to zero and no distillable entanglement can be shared between distant qudits a and b:

$$\begin{aligned} N(\Omega _{ab}^{(0)})=\left\{ \begin{array}{ll} \frac{d-(d+1)p}{d+(d-1)p},&{}\quad 0\le p\le p_c\\ 0,&{}\quad p_c\le p \le 1 \end{array}\right. . \end{aligned}$$

(C10)

Hence, for $p\le p_c$ average of distillable entanglement between a and b is turned out to be

$$\begin{aligned} \bar{N}_{a|b}(\Omega _{ab})=p_sN_{a|b}\left( \Omega _{ab}^{(0)}\right) =\frac{d-(d+1)p}{d(2d-1)}, \end{aligned}$$

(C11)

and for $p>p_c$ this quantity is zero. It is worth noticing that state of three qudits before the final measurement has block-diagonal form, that is

$$\begin{aligned} \Omega ^{(2)'}_{abc}=p_s\Omega _{ab}^{(0)}\otimes |0\rangle \langle 0|+\sum _{i=1}^{d-1}p_i\Omega _{ab}^{(i)}\otimes |i\rangle \langle i|, \end{aligned}$$

(C12)

where $\Omega _{ab}^{(i)}$ for $i=1\ldots d-1$ are separable states. Regarding this block-diagonal form of $\Omega ^{(2)'}_{abc}$ and following the same arguments as in Sect. 4, we conclude that

$$\begin{aligned} N_{a|bc}\left( \Omega ^{(2)'}_{abc}\right) =N_{b|ac}\left( \Omega ^{(2)'}_{abc}\right) =\bar{N}_{a|b}(\Omega _{ab}), \end{aligned}$$

(C13)

where the first equality is due to the fact that $\Omega ^{(2)'}_{abc}$ in Eq. (C5) is invariant under permutation of indices a and b. Furthermore, since unitary action on qudits b and c cannot change the entanglement between partitions a and bc, we have

$$\begin{aligned} N_{a|bc}\left( \Omega ^{(1)'}_{abc}\right) =N_{b|ac}\left( \Omega ^{(2)'}_{abc}\right) . \end{aligned}$$

(C14)

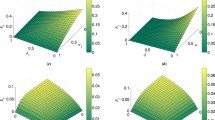
Hence, what we found for distributing two-qubit entangled state is valid for arbitrary dimension. That is, while exchange particle is always in separable state with rest of the system, as long as distillable entanglement between partitions a|bc and b|ac is not vanishing due to the noise, it is possible to distribute distillable entanglement between distant qudits by probabilistic EDSS protocol. Figure 6 shows average distillable entanglement $\bar{N}_{a|b}(\Omega _{ab})$ shared between qudits a and b versus noise parameter p for $d=2$ (red dashed line), $d=3$ (blue dash-dotted line) and $d=6$ (green solid line). As it is seen in this figure, by increasing the dimension of Hilbert space, the entanglement decreases more slowly with p. It means that as the dimension increases the protocol is useful for distributing entanglement up to higher value of noise parameter which is given by $p_c$. Figure 7 shows the increase in $p_c$ versus d, dimension of Hilbert space.

Fig. 6

Average entanglement shared between qudits a and b [Eq. (C11)] versus noise parameter p for $d=2$ (dashed red line), $d=3$ (dot dashed blue line) and $d=6$ (solid green line) when communication channel is depolarizing channel

Fig. 7

Critical value of error parameter $p_{c}$ versus d (dimension of Hilbert space), beyond which distillable entanglement cannot be distributed between distant qudits a and b by mediating particle c when communication channel is depolarizing channel

1.2 2. Amplitude damping noise

This part is devoted to analyse the effect of amplitude damping noise on d-dimensional EDSS protocol. Amplitude damping channel on qudits is defined by

$$\begin{aligned} \mathcal {E}(\rho )=\sum _{m=0}^{d-1}E_{m}\rho E_{m}^{\dagger }, \end{aligned}$$

(C15)

in which

$$\begin{aligned} E_{0}= & {} \vert 0\rangle \langle 0\vert +\sum _{i=1}^{d-1}\sqrt{1-\gamma }\vert i\rangle \langle i|\nonumber \\ E_{m}= & {} \sqrt{\gamma }\vert 0\rangle \langle m\vert ,\quad 1\le m\le d-1. \end{aligned}$$

(C16)

By applying amplitude damping noise on qudit c of state in Eq. (C2), we have:

$$\begin{aligned} \Omega ^{(1)'}_{abc}= & {} \mathcal {E}_{c}\left( \Omega ^{(1)}_{abc}\right) \nonumber \\= & {} \frac{1}{d(2d-1)}\left( \gamma (d-1)\Pi _{000}+\Pi _0\otimes I\otimes \Pi _0\right. \nonumber \\&\left. +\sum _{m=1}\left( \sqrt{1-\gamma }(|0\rangle \langle m|^{\otimes 3}+|m\rangle \langle 0|^{\otimes 3})\right. \right. \nonumber \\&\left. \left. +{(1+\gamma (d-1))}\Pi _{mm0}\right) +\sum _{m,n=1}(1-\gamma )\vert m\rangle \langle n\vert ^{\otimes 3}\right. \nonumber \\&\left. +\sum _{m\ne n}\sum _{n=1}\left( (1-\gamma )(\Pi _{mmn}+\Pi _{nmn})+\gamma \Pi _{nm0}\right) \right) \end{aligned}$$

(C17)

After applying inverse of $\mathrm {CNOT}$ on qudits b and c, state of three qudits is as follows:

$$\begin{aligned} \Omega ^{(2)'}_{abc}=\sum _{m=0}^{d-1}p_{m}\Omega ^{(m)}_{ab}\otimes |m\rangle \langle m|, \end{aligned}$$

(C18)

It is straightforward to show that when Bob measures qudit c in computational basis, if outcome is $|0\rangle$ shared state between a and b is entangled; otherwise, it is separable. Therefore, by probability

$$\begin{aligned} p_{0}=\frac{d+(d-1)\gamma }{d(2d-1)}, \end{aligned}$$

(C19)

entangled state

$$\begin{aligned} \Omega ^{(0)}_{ab}= & {} \frac{1}{d+(d-1)\gamma }\Bigg (\big (1+\gamma (d-1)\big )\Pi _{00}\nonumber \\&\quad +\sum _{m,n=1}(1-\gamma )\vert m\rangle \langle n\vert ^{\otimes 2}\nonumber \\&\quad +\sum _{m=1}^{d-1}\Big (\gamma \Pi _{m0}+\sqrt{1-\gamma }(|0\rangle \langle m|^{\otimes 2}+|m\rangle \langle 0|^{\otimes 2})\Big )\Bigg ) \end{aligned}$$

(C20)

is shared between qudits a and b. Entanglement of this state is given by

$$\begin{aligned} N_{a|b}(\Omega ^{(0)}_{ab})=\frac{d(1-\gamma )}{d+(d-1)\gamma },\quad 0\le \gamma \le 1. \end{aligned}$$

(C21)

Hence, the average shared entanglement between a and b is equal to:

$$\begin{aligned} \bar{N}_{a|b}(\Omega _{ab})=p_{0}N_{a|b}(\Omega ^{(0)}_{ab})=\frac{1-\gamma }{2d-1}. \end{aligned}$$

(C22)

Furthermore, the block-diagonal form of state in Eq. (C18), and the same reasoning of Sect. 4 results that

$$\begin{aligned} N_{a|bc}\left( \Omega ^{(2)'}_{abc}\right) =N_{b|ac}\left( \Omega ^{(2)'}_{abc}\right) =N_{a|bc}\left( \Omega ^{(1)'}_{abc}\right) =\bar{N}_{a|b}\left( \Omega _{ab}\right) . \end{aligned}$$

(C23)

Hence, while exchange particle is always in separable state with rest of the system, since distillable entanglement between partitions a|bc and b|ac is not vanishing due to the noise, it is possible to distribute distillable entanglement between distant qudits by probabilistic EDSS protocol. Figure 8 shows average distillable entanglement shared between qudits a and b versus noise parameter $\gamma$ for $d=2$ (red dashed line), $d=3$ (blue dash-dotted line) and $d=6$ (green solid line). For amplitude damping channel we see that as the dimension of the Hilbert state increases, the amount of average entanglement distributed between qudits a and b decreases.

Fig. 8

Average entanglement shared between qudits a and b [Eq. (C22)] versus noise parameter $\gamma$ for $d = 2$ (dashed red line), $d = 3$ (dot dashed blue line) and $d = 6$ (solid green line)