Quantum walking in curved spacetime

Abstract

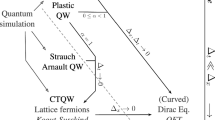
A discrete-time quantum walk (QW) is essentially a unitary operator driving the evolution of a single particle on the lattice. Some QWs admit a continuum limit, leading to familiar PDEs (e.g., the Dirac equation). In this paper, we study the continuum limit of a wide class of QWs and show that it leads to an entire class of PDEs, encompassing the Hamiltonian form of the massive Dirac equation in ($1+1$) curved spacetime. Therefore, a certain QW, which we make explicit, provides us with a unitary discrete toy model of a test particle in curved spacetime, in spite of the fixed background lattice. Mathematically, we have introduced two novel ingredients for taking the continuum limit of a QW, but which apply to any quantum cellular automata: encoding and grouping.

Appendices

Appendix 1: Calculation of the first-order expansion of the discrete model

In this section we prove Eq. (20), which we reproduce here:

$$\begin{aligned} \begin{bmatrix}2 \varepsilon \partial _t u \\ 2\varepsilon \partial _t d \\ u' \\ d'\end{bmatrix} =&(I \oplus U) \begin{bmatrix} 0 \\ 0 \\ u' \\ d' \end{bmatrix} + (I \oplus U) B \begin{bmatrix} 2u' \\ 2d' \\ 0 \\ 0 \end{bmatrix} + \varepsilon \left\{ (2N-\mathrm {i}\tilde{E})(I\oplus U) \right. \nonumber \\&\left. + (I \oplus U) (\mathrm {i}\tilde{E}+2M) + T \right\} \begin{bmatrix} u \\ d \\ 0 \\ 0 \end{bmatrix}. \end{aligned}$$

(44)

Recall that we want to expand

$$\begin{aligned} \phi _{\mathrm{out}}(t,x)&= G~\phi _{\mathrm{in}}(t,x), \end{aligned}$$

(45)

where

$$\begin{aligned} G&= E^\dagger (t+2,x) W'(t,x) (P' \oplus P) (E(t,x-2)\oplus E(t,x+2)). \end{aligned}$$

(46)

The first-order expansion of the encoding and of the walk is, by definition,

$$\begin{aligned} E(t,x)&= E^{(0)}(t,x) + \varepsilon \mathrm {i}E^{(0)}(t,x)\tilde{E}(t,x) + O(\varepsilon ^2) \end{aligned}$$

(47)

$$\begin{aligned} W'(t,x)&= W^{(0)}(t,x) + \varepsilon \mathrm {i}W^{(0)}(t,x)\tilde{W}(t,x) + O(\varepsilon ^2), \end{aligned}$$

(48)

hence, to first order in $\varepsilon$, the operators in (46) expand to

$$\begin{aligned}&E^{\dagger }(t+2,x) \simeq E^{(0)\dagger } + \varepsilon \left( 2 \partial _t E^{(0)\dagger } -\mathrm {i}\tilde{E}E^{(0)\dagger } \right) \end{aligned}$$

(49)

$$\begin{aligned}&W'(t,x) \simeq W^{(0)}+\varepsilon \mathrm {i}W^{(0)}\tilde{W} \end{aligned}$$

(50)

$$\begin{aligned}&E(t,x-2)\oplus E(t,x+2) \nonumber \\&\quad \simeq \left( E^{(0)} - 2 \varepsilon \partial _x E^{(0)} + \mathrm {i}\varepsilon E^{(0)}\tilde{E} \right) \oplus \left( E^{(0)} + 2 \varepsilon \partial _x E^{(0)} + \mathrm {i}\varepsilon E^{(0)}\tilde{E} \right) \end{aligned}$$

(51)

where in the right-hand side all operators are evaluated at (t, x). Recall that the first-order expansions of the output and input are

$$\begin{aligned} \phi _{\mathrm{out}}(t,x) \simeq \begin{bmatrix} u \\ d \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 2\varepsilon \partial _t u \\ 2\varepsilon \partial _t d \\ u' \\ d' \end{bmatrix}, \quad \phi _{\mathrm{in}}(t,x) \simeq \begin{bmatrix} u \\ d \\ 0 \\ 0 \end{bmatrix} \oplus \begin{bmatrix} u \\ d \\ 0 \\ 0\end{bmatrix} + \begin{bmatrix} -2u' \\ -2d' \\ u' \\ d' \end{bmatrix} \oplus \begin{bmatrix} 2u' \\ 2d' \\ u' \\ d' \end{bmatrix}. \end{aligned}$$

(52)

We shall use the identities

$$\begin{aligned}&( P' \oplus P) (E \oplus E) (v \oplus v) = XEv \end{aligned}$$

(53)

$$\begin{aligned}&(P' \oplus P) (E \oplus E) (-v \oplus v) = XZEv \end{aligned}$$

(54)

valid for any $v \in \mathbb {C}^4$, because $P'$ (resp. P) are the projections onto the primed (resp. non-primed) coordinates; in matrix form,

$$\begin{aligned} P' = \begin{pmatrix} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{pmatrix}, \quad P = \begin{pmatrix} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \end{pmatrix}. \end{aligned}$$

(55)

Next we plug the previous expansions into (45). Collecting all the terms of first order in $\varepsilon$,

$$\begin{aligned} \begin{bmatrix} 2\varepsilon \partial _t u \\ 2\varepsilon \partial _t d \\ u' \\ d' \end{bmatrix} =&E^{(0) \dagger } W^{(0)} X E^{(0)} \begin{bmatrix} 0 \\ 0 \\ u' \\ d' \end{bmatrix} + E^{(0) \dagger } W^{(0)} X Z E^{(0)} \begin{bmatrix} 2u' \\ 2d' \\ 0 \\ 0 \end{bmatrix} \\&+\left\{ \varepsilon (2\partial _t E^{(0)\dagger } -\mathrm {i}\tilde{E}E^{(0) \dagger } )W^{(0)} X E^{(0)} + \mathrm {i}\varepsilon E^{(0)\dagger } W^{(0)} \tilde{W} X E^{(0)} \right. \\&\left. + \mathrm {i}\varepsilon E^{(0)\dagger }W^{(0)} X E^{(0)}\tilde{E} + 2 \varepsilon E^{(0)\dagger } W^{(0)} X Z \partial _x E^{(0)} \right\} \begin{bmatrix} u \\ d \\ 0 \\ 0 \end{bmatrix}. \end{aligned}$$

Next we use the zeroth-order condition (cf. (19)), namely $E^{(0)\dagger } W^{(0)} X E^{(0)} = I \oplus U$, so that

$$\begin{aligned} \begin{bmatrix} 2\varepsilon \partial _t u \\ 2\varepsilon \partial _t d \\ u' \\ d' \end{bmatrix}&= (I \oplus U) \begin{bmatrix} 0 \\ 0 \\ u' \\ d' \end{bmatrix} + (I\oplus U) \underbrace{E^{(0) \dagger } Z E^{(0)}}_{\mathrm {B }} \begin{bmatrix} 2u' \\ 2d'\\ 0 \\ 0 \end{bmatrix} \\&\quad \times \varepsilon \left\{ \left[ 2\underbrace{(\partial _t E^{(0) \dagger })E^{(0)}}_{\mathrm {N}} -\mathrm {i}\tilde{E} \right] (I\oplus U ) + \underbrace{\mathrm {i}E^{(0)\dagger } W^{(0)}\tilde{W} X E^{(0)}}_{\mathrm {T}} \right. \\&\quad \left. +\, \mathrm {i}(I\oplus U) \tilde{E} + 2 (I\oplus U) \underbrace{E^{(0)\dagger } Z \partial _x E^{(0)}}_{\mathrm {M}} \right\} \begin{bmatrix} u \\ d \\ 0 \\ 0 \end{bmatrix}, \end{aligned}$$

and we get the desired result.

Appendix 2: General form of B

Since B must be Hermitian, cf. (21a), then $B_1$ and $B_4$ are Hermitian. Since it is also unitary, then it must square to the identity. This implies that the conditions

$$\begin{aligned} B_1^2 + B_2^\dagger B_2&= {\text {Id}}_2 \end{aligned}$$

(56a)

$$\begin{aligned} B_4^2 + B_2 B_2^\dagger&= {\text {Id}}_2 \end{aligned}$$

(56b)

and

$$\begin{aligned} B_2 B_1 + B_4 B_2&= 0 \end{aligned}$$

(57a)

$$\begin{aligned} B_1 B_2^\dagger + B_2^\dagger B_4&= 0 \end{aligned}$$

(57b)

must hold. Note also that B must have a complete set of orthonormal eigenvectors, eigenvalues $\pm 1$, and it shall be traceless, because it is similar to Z.

First, we parameterize the block $B_2$. Consider the spectral decomposition of $B_1 = V D V^\dagger$, $D = \text {diag}\{ d_1,d_2\}$. From the first of conditions (56a), we have that $d_1,d_2 \in [-1,1]$, because the square root of the components of ${\text {Id}}-D^2$ is precisely the singular values of $B_2$, which should be nonnegative. Next, we shall find $B_2$ such that constraint (34a) is satisfied. The same equation also determines U.

We look for $B_2 \in \mathbb {C}^{2\times 2}$ such that conditions (34a) and (56a) are satisfied, namely that

• 1. ${\text {Id}}+ 2 B_2$ is unitary,

• 2. $B_2^\dagger B_2 = {\text {Id}}- B_1^2$.

To prove our lemma we will use a shortcut provided by the following characterization of matrices with positive definite [26] real part. Recall that if $A \in \mathbb {C}^{n\times n}$, its real and imaginary parts are $\mathfrak {R}A := \frac{1}{2}( A+A^\dagger )$ and $\mathfrak {I}A = \frac{1}{2\mathrm {i}} (A-A^\dagger )$, respectively.

Theorem 1

(see [27]) Let $A \in \mathbb {C}^{n\times n}$. Then, $\mathfrak {R}A$ is positive definite if and only if

$$\begin{aligned} A = T \begin{pmatrix} 1+\mathrm {i}\alpha _1 &{} &{} \\ &{} \ddots &{} \\ &{} &{} 1 + \mathrm {i}\alpha _n \end{pmatrix} T^\dagger \end{aligned}$$

(58)

for some non-singular T and $\alpha _1,\ldots ,\alpha _n \in \mathbb {R}$.

Note that, from condition 1 above,

$$\begin{aligned} ({\text {Id}}+ 2 B_2^\dagger )({\text {Id}}+ 2 B_2) = {\text {Id}}\Rightarrow B_2 + B_2^\dagger + 2 (B_2^\dagger B_2) = 0, \end{aligned}$$

(59)

hence condition 1 is equivalent to $\mathfrak {R}B_2 = -B_2^\dagger B_2$. Recall that $A^\dagger A$ is positive definite for any $A \in \mathbb {C}^{n\times n}$, hence Theorem 1 can be applied to $-B_2$.

We recall the following parameterization of the U(2) group, namely that

$$\begin{aligned} U(2) = \left\{ e^{\mathrm {i}\theta } \begin{pmatrix} \alpha &{} \beta \\ -\overline{\beta } &{} \overline{\alpha } \end{pmatrix} : \theta \in [0,2\pi ),~\alpha ,\beta \in \mathbb {C},~|\alpha |^2+|\beta |^2 = 1 \right\} . \end{aligned}$$

(60)

Lemma 1

Let $B_1 \in \mathbb {C}^{2\times 2}$ be Hermitian, with spectral decomposition $B_1 = V_1 D_1 V_1^\dagger$, and eigenvalues $d_1,d_2 \in [-1,1] \in \mathbb {R}$. Assume that $B_2 \in \mathbb {C}^{2\times 2}$ satisfies the conditions

• 1. $\mathfrak {R}B_2 = -B_2^\dagger B_2$,

• 2. $B_2^\dagger B_2 = {\text {Id}}- B_1^2$.

Let $\lambda _{i} = \sqrt{{1-d_{i}^2}}$, and $\eta _1 \in \{\eta _1^+, \eta _1^-\}$, $\eta _2 \in \{\eta _2^+, \eta _2^-\}$, with $\eta _i^+ \in [0,\pi /2]$, $\eta _i^- \in [-\pi /2,0]$, and such that $\sin \eta ^\pm _{i} = \pm |d_{i}|$ for any $i \in \{1,2 \}$. Then,

• 1. If $d_1^2 \ne d_2^2$ (non-degenerate case), then

  $$\begin{aligned} B_2 = -V_1 \begin{pmatrix} \lambda _{1} e^{\mathrm {i}\eta _1} &{} 0 \\ 0 &{} \lambda _{2} e^{\mathrm {i}\eta _2} \end{pmatrix} V_1^\dagger . \end{aligned}$$

  (61)

• 2. If $d_1^2 = d_2^2$ and $\eta _1 = \eta _2$, then $B_2 = -\lambda _1 e^{\mathrm {i}\eta _1} {\text {Id}}$.

• 3. If $d_1^2 = d_2^2$ and $\eta _1 = -\eta _2$, then

  $$\begin{aligned} B_2 = -\lambda _1 K e^{\mathrm {i}\eta _1\sigma _z} K^\dagger , \end{aligned}$$

  (62)

  for any $K \in U(2)$. We remark that any two $K_{1,2}$ such that $K_1 = K_2 K'$ for some $K'$ of the form $K' = \cos (\theta ){\text {Id}}+ \mathrm {i}\sin (\theta )\sigma _z$, will give the same $B_2$.

Proof

From Theorem 1, and condition 1, $B_2$ can be written as $B_2 = -T_2 D_2 T_2^\dagger$ for some non-singular $T_2$ and $D_2 = \text {diag}\{ 1+\mathrm {i}\alpha _1,1+\mathrm {i}\alpha _2 \}$, $\alpha _1,\alpha _2 \in \mathbb {R}$. Substitution into condition 1 gives

$$\begin{aligned} T_2^\dagger T_2 = \begin{pmatrix} (1+\alpha _1^2)^{-1} &{} 0 \\ 0 &{} (1+\alpha _2^2)^{-1} \end{pmatrix}. \end{aligned}$$

(63)

Now, let the SVD of $T_2 = W \Sigma V^\dagger$. Then $T_2^\dagger T_2 = V \Sigma ^2 V^\dagger$ and using (63) it is easy to see, using the canonical decomposition of unitary matrices (cf. (60)), that we must have one of the following cases:

• 1. If $\alpha _1^2 \ne \alpha _2^2$, then for some $\theta _1,\theta _2 \in [0,2\pi )$, either

  • (a) $\Sigma = \begin{pmatrix} \frac{1}{\sqrt{1+\alpha _2^2}} &{} 0 \\ 0 &{} \frac{1}{\sqrt{1+\alpha _1^2}} \end{pmatrix}$ and $V = \begin{pmatrix} 0 &{} e^{\mathrm {i}\theta _1} \\ e^{\mathrm {i}\theta _2} &{} 0 \end{pmatrix}$. Hence, $B_2 = - W \begin{pmatrix} \frac{1+\mathrm {i}\alpha _2}{1+\alpha ^2_2} &{} 0 \\ 0 &{} \frac{1+\mathrm {i}\alpha _1}{1+\alpha ^2_1} \end{pmatrix} W^\dagger$.

  • (b) $\Sigma = \begin{pmatrix} \frac{1}{\sqrt{1+\alpha _1^2}} &{} 0 \\ 0 &{} \frac{1}{\sqrt{1+\alpha _2^2}} \end{pmatrix}$ and $V = \begin{pmatrix} e^{\mathrm {i}\theta _1} &{} 0 \\ 0 &{} e^{\mathrm {i}\theta _2} \end{pmatrix}$. Hence, $B_2 = - W \begin{pmatrix} \frac{1+\mathrm {i}\alpha _1}{1+\alpha ^2_1} &{} 0 \\ 0 &{} \frac{1+\mathrm {i}\alpha _2}{1+\alpha ^2_2} \end{pmatrix} W^\dagger$. Note that in either case, we can write $B_2 = - W \text {diag}\left\{ \frac{1+\mathrm {i}\alpha _{\sigma (1)}}{1+\alpha ^2_{\sigma (1)}}, \frac{1+\mathrm {i}\alpha _{\sigma (2)}}{1+\alpha ^2_{\sigma (2)}} \right\} W^\dagger$, where $\sigma : \{ 1,2\} \rightarrow \{ 1,2\}$ is a permutation. It is easy to check that condition 1 is indeed satisfied. Next, substitution into condition 2 gives

    $$\begin{aligned} \begin{pmatrix} 1-d_1^2 &{} 0 \\ 0 &{} 1-d_2^2 \end{pmatrix} = K \begin{pmatrix} \frac{1}{1+\alpha _{\sigma (1)}^2} &{} 0 \\ 0 &{} \frac{1}{1+\alpha _{\sigma (2)}^2} \end{pmatrix} K^\dagger , \end{aligned}$$

    (64)

    with $K := V_1^\dagger W \in U(2)$. Again, we use the canonical form, cf. (60), to find that K is diagonal or antidiagonal, with two independent phases. Introducing back W into $B_2$, in either case we have $\alpha _{i}^2 = \frac{d_{i}^2}{1-d_{i}^2}$, $i=1,2$, hence $\alpha _{i} = \pm \frac{|d_i|}{\sqrt{1-d_i^2}}$, so

    $$\begin{aligned} \frac{1+\mathrm {i}\alpha _{i}}{1+\alpha ^2_{i}} = \sqrt{{1-d_{i}^2}}\left( \sqrt{{1-d_{i}^2}} \pm \mathrm {i}|d_{i}| \right) = \sqrt{{1-d_{i}^2}} e^{\mathrm {i}\eta ^\pm _{i}}, \end{aligned}$$

    (65)

    provided that $\cos \eta ^\pm _{i} = \sqrt{{1-d_{i}^2}}$, and $\sin \eta ^\pm _{i} = \pm |d_{i}|$. This proves part 1.

• 2. If $\alpha _1^2 = \alpha _2^2$, then $\Sigma = \frac{1}{\sqrt{1+\alpha _1^2}} {\text {Id}}_2$, and $V \in U(2)$ is arbitrary. Thus, we can write $B_2 = -\frac{1}{1+\alpha _1^2} K \begin{pmatrix} 1+\mathrm {i}\alpha _1 &{} 0 \\ 0 &{} 1\pm \mathrm {i}\alpha _1 \end{pmatrix} K^\dagger$ for some $K \in U(2)$. Substitution into condition 2 gives $\alpha _1^2 = d_1^2 / (1-d_1^2)$, and proceeding as in (65), we obtain the claim.$\square$

Next we characterize $B_4$. We assume that the relevant constraints from (56a)-(57b) are satisfied, namely $B_1^2 + B_2^\dagger B_2 = {\text {Id}}_2$ and that $B_4^2 + B_2 B_2^\dagger = {\text {Id}}_2$.

Lemma 2

In the hypothesis of above,

• 1. If $d_1^2 \ne d_2^2$ (non-degenerate case), then $B_4=-B_1$.

• 2. If $d_1 = d_2$, then $B_4 = -B_1$.

• 3. If $d_1 = -d_2$, then

  $$\begin{aligned} B_4= d_1 K \sigma _z K^\dagger , \end{aligned}$$

  (66)

  for any $K \in U(2)$. We remark that any two $K_{1,2} \in U(2)$ such that $K_1 = K_2 K'$ for some $K'$ of the form $K' = \cos (\theta ){\text {Id}}+ \mathrm {i}\sin (\theta )\sigma _z$, will give the same $B_4$.

Proof

From (34a), $B_2$ is normal; then, from (56a) and (56b) we have that $B_1^2=B_4^2$. Since $B_4$ is Hermitian consider its spectral decomposition, $B_4=W D_4 W^\dagger$, $W \in U(2)$. Then, $D_4^2 = K D_1^2 K^\dagger$, where $K := W^\dagger V_1$. Using the canonical form (60), we find that

• 1. If $d_1^2 \ne d_2^2$, then K is either diagonal or antidiagonal, with arbitrary phases. In either case we obtain $B_4 = V_1\text {diag}\{ \pm d_1,\pm d_2 \} V_1^\dagger$, but since we must have $\text {Tr}B_4=-\text {Tr}B_1$, we shall take $-d_1$, $-d_2$. Hence, $B_4=-B_1$.

• 2. If $d_1^2 = d_2^2$, then $K \in U(2)$ is arbitrary, and we have $B_4 = V_1 K^\dagger \text {diag}\{ \pm d_1,\pm d_1 \} K V_1^\dagger$. If $d_1=d_2$, then $\text {Tr}B_4 = -2d_1$, so $B_4 = -d_1 {\text {Id}}_2 = -B_1$. If $d_1=-d_2$, then $\text {Tr}B_4=0$, and we can take $d_1,-d_1$ or $-d_1, d_1$. $\square$