Abstract
For analyzing conflict between two large open countries over external territories rich in natural resources, we develop a game-theoretic model of trade under resource appropriation possibilities. We show that greater trade openness (by lowering trade costs) reduces the overall intensity of arming when the adversary countries are symmetric in all dimensions. This finding is consistent with the liberal peace hypothesis that trade reduces conflict. We further analyze how equilibrium is affected by differences in national resource endowments. The resulting asymmetric equilibrium reveals that arming by the more endowed country exceeds that of the less endowed country and the two adversaries respond to lower trade costs differently: the more endowed country cuts back on its arming, whereas the less endowed country may increase it. Under resource endowment asymmetry, the aggregate arming allocations of the adversaries could increase despite greater trade openness.




Similar content being viewed by others
Notes
For studies that present empirical evidence on the correlation between trade, conflict and related issues, see, e.g., Polachek (1992), Barbieri (1996), Barbieri and Levy (1999), Reuveny and Kang (1998), Polachek et al. (1999), Barbieri and Schneider (1999), Anderton and Carter (2001), Mansfield and Pollins (2001, 2003), Levy and Barbieri (2004), Kim and Rousseau (2005), and Glick and Taylor (2010).
The book by Mansfield and Pollins (2003) contains studies of the trade and conflict debate. The contribution by Oneal and Russett (1999) supports Polachek (1980) and shows that strengthening the extent of trade openness between contending countries effectively can reduce their conflicts in terms of overall armament expenditures. Nevertheless, some studies (e.g., Kim and Rousseau 2005) find that the pacifying effect of greater trade openness can be neutral; other studies (e.g., Barbieri 1996) find that extensive trade linkages may increase the probability of armed conflicts. Barbieri and Levy (1999) show that war does not have significant impacts on trading relationships between adversaries.
Conflicts between nations for valuable resources reflect international competition for rents through non-market means. We hypothesize that each nation has an aggregate payoff function and devotes efforts or resources into international rent-seeking activities (i.e., fighting) for more resources. We abstract our analysis from destruction costs. For studies on conflict that takes into account the endogeneity of destruction costs see, e.g., Sanders and Walia (2014), and Chang et al. (2015), and Chang and Luo (2017).
The modeling approach herein thus stands in contrast to the traditional assumption of "small open economies" in neoclassical international trade analysis, wherein trading nations accept the prices of tradable goods in their world markets under perfect competition.
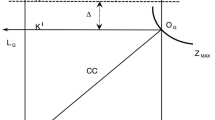
We thank an anonymous referee for valuable suggestions to consider reinforcement of borders as part of arming expenditures. This makes trade costs to be determined endogenously determined by arming choices. To focus on disputes over an external territory, our analysis abstracts from conflict over national endowments, which are taken to be secured. That is, the analysis abstracts from border issues of the contending countries. Our simple analysis considers arming expenditures by each country as the number of guns required for occupying the territory so as to acquire its valuable resource or intermediate input for final good production. The term "trade costs" refers to the purely economic costs of engaging in bilateral trade according to the traditional international economics analysis. One advantage of this traditional treatment of trade costs is to see how economic decisions (in exporting and importing different final goods) affects military decisions (in terms of conflict-related resources allocated to armaments production). For ease of showing the relationship between trade decisions and military decisions, we consider trade costs to be exogenous in the analysis. The endogeneity of trade costs would add analytical complexity. We wish to pursuit this interesting extension in our future research.
For the case of symmetry in all dimensions that shall be discussed in the latter part of this section, we see that this inequality condition implies that \(Z < 4G,\) where \(G = G_{A} = G_{B} .\) The inequality condition then indicates that \(G > {Z \mathord{\left/ {\vphantom {Z 4}} \right. \kern-0pt} 4}.\) That is, each country's arming is strictly greater than a quarter of its national resource endowment.
That condition guarantees that the equilibrium prices and quantities of the final goods are positive under symmetry.
Note that country A's arming reaction curve, \(G_{A}^{S} (G_{B} ),\) is implicitly defined by its FOC that \({{\partial \varPi_{A} } \mathord{\left/ {\vphantom {{\partial \varPi_{A} } {\partial G_{A} }}} \right. \kern-0pt} {\partial G_{A} }} = 0\) and country B's arming reaction curve, \(G_{B}^{S} (G_{A} ),\) is implicitly defined by its FOC that \({{\partial \varPi_{B} } \mathord{\left/ {\vphantom {{\partial \varPi_{B} } {\partial G_{B} }}} \right. \kern-0pt} {\partial G_{B} }} = 0.\)
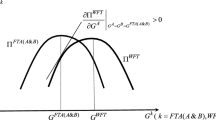
We thank an anonymous referee for valuable suggestions to discuss whether the arming levels are strategic substitutes or strategic complements. We find that they are strategic complements under symmetry. For the case in which there is asymmetry in national endowments, the arming levels may be strategic substitutes. We present the case of asymmetry in Sect. 3.
The parameter \(\delta\) may be used to represent the country size differential between A and B in that the higher the value of \(\delta\) the greater the size of country A relative to country B.
We owe thanks to an anonymous referee in providing us this important point for further study.
Garfinkel and Syropoulos (2017) examine the case where two adversaries do not trade with each other but do engage in trade with a third country. For issues on how the equilibrium outcome of a two-party conflict is altered by the strategic involvement of an outside party, see Chang et al. (2007), Chang and Sanders (2009), Sanders and Walia (2014). But these three studies do not consider the possibility of bilateral trade between adversaries.
References
Acemoglu, D., Golosov, M., Tsyvinski, A., & Yared, P. (2012). A dynamic theory of resource wars. Quarterly Journal of Economics, 121, 283–331.
Anderton, C. H., & Carter, J. R. (2001). The impact of war on trade: An interrupted times-series study. Journal of Peace Research, 38, 445–457.
Bagwell, K., & Staiger, R. W. (1997). Multilateral cooperation during the formation of free trade areas. International Economic Review, 38, 291–319.
Barbieri, K. (1996). Economic interdependence: a path to peace or a source of interstate conflict? Journal of Peace Research, 33, 29–49.
Barbieri, K., & Levy, J. S. (1999). Sleeping with the enemy: The impact of war on trade. Journal of Peace Research, 36, 463–479.
Barbieri, K., & Schneider, G. (1999). Globalization and peace: Assessing new directions in the study of trade and conflict. Journal of Peace Research, 36, 387–404.
Chang, Y.-M., & Luo, Z. (2017). Endogenous destruction in conflict: Theory and extensions. Economic Inquiry, 55, 479–500.
Chang, Y.-M., Potter, J., & Sanders, S. (2007). War and peace: Third-party intervention in conflict. European Journal of Political Economy, 23, 954–974.
Chang, Y.-M., & Sanders, S. (2009). Raising the cost of rebellion: The role of third-party intervention in intrastate conflict. Defence and Peace Economics, 20, 149–169.
Chang, Y.-M., Sanders, S., & Walia, B. (2015). The costs of conflict: a choice-theoretic, equilibrium analysis. Economics Letters, 131, 62–65.
Findlay, R., & O’Rourke, K. (2010). War, trade and natural resources: A historical perspective. In M. R. Garfinkel & S. Skaperdas (Eds.), The Oxford Handbook of the Economics of Peace and Conflict. Oxford: Oxford University Press.
Garfinkel, M. R., Skaperdas, S., & Syropoulos, C. (2015). Trade and insecure resources. Journal of International Economics, 95, 98–114.
Garfinkel, M. R., & Syropoulos, C. (2017). Trade with the enemy: could the classic liberals be right?. Unpublished manuscript.
Glick, R., & Taylor, A. M. (2010). Collateral damage: Trade disruption and the economic impact of war. Review of Economic Statistics, 92, 102–127.
Hirshleifer, J. (1989). Conflict and rent-seeking success functions: ratio vs. difference models of relative success. Public Choice, 63, 101–112.
Kim, Y. S., & Rousseau, D. L. (2005). The classical liberals were right (or half wrong): new tests of the ‘liberal peace’, 1960–88. Journal of Peace Research, 42, 523–543.
Levy, J. S., & Barbieri, K. (2004). Trading with the enemy during wartime. Security Studies, 13, 1–47.
Mansfield, E. D., & Pollins, B. M. (2001). The study of interdependence and conflict: recent advances, open questions, and directions for future research. Journal of Conflict Resolution, 45, 834–859.
Mansfield, E. D., & Pollins, B. M. (2003). Economic interdependence and international conflict: New perspectives on an enduring debate. Ann Arbor: University of Michigan Press.
Martin, P., Mayer, T., & Thoenig, M. (2008). Make trade not war. Review of Economic Studies, 75, 865–900.
Martin, P., Mayer, T., & Thoenig, M. (2012). The geography of conflicts and regional trade agreements. American Economics Journal: Macroeconomics, 4, 1–35.
Oneal, J. R., & Russett, B. (1999). Assessing the liberal peace with alternative specifications: Trade still reduces conflict. Journal of Peace Research, 36, 423–442.
Polachek, S. M. (1980). Conflict and trade. Journal of Conflict Resolution, 24, 55–78.
Polachek, S. M. (1992). Conflict and trade: an economics approach to political international interactions. In I. Walter & C. Anderton (Eds.), Economics of arms reduction and the peace process (pp. 89–120). Amsterdam: Elsevier Science.
Polachek, S. W., Robst, J., & Chang, Y.-C. (1999). Liberalism and interdependence: Extending the trade-conflict model. Journal of Peace Research, 36, 405–422.
Reuveny, R., & Kang, H. (1998). Bilateral trade and political conflict/cooperation: Do goods matter? Journal of Peace Research, 35, 581–602.
Sanders, S., & Walia, B. (2014). Endogenous destruction in a model of armed conflict: Implications for conflict intensity, welfare, and third-party intervention. Journal of Public Economic Theory, 16, 604–609.
Skaperdas, S. (1996). Contest success functions. Economic Theory, 7, 283–290.
Skaperdas, S., & Syropoulos, C. (2001). Guns, butter, and openness: On the relationship between security and trade. American Economic Review, Papers and Proceedings, 91, 353–357.
Tullock, G. (1980). Efficient rent seeking. In J. Buchanan, R. Tollison, & G. Tullock (Eds.), Towards a theory of the rent-seeking society. Texas: Texas A&M University Press.
Acknowledgements
We are indebted to William F. Shughart II, the Editor in Chief, and two anonymous reviewers for insightful comments and valuable suggestions, which have significantly improved the paper. An earlier version of this paper was presented in the conflict/security sessions at the International Conference on Game Theory, Stony Brook University, July 17–21, 2017. We acknowledge helpful comments from the session organizers Timothy Mathews, Shane Sanders, as well as conference participants. All remaining errors are ours.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Appendix 1: Equilibrium prices, consumer surplus, and producer surplus
After substituting \(X_{A}\) from (2a) and \(Y_{B}\) from (2b) into the final good prices in (11), we have:
Substituting these equilibrium prices into the demand equations in (3), we then use Eqs. (4) and (5) to calculate consumer and producer surplus. For country A, we have
For country B, we have
1.2 Appendix 2: Decomposing the effect of country A’s arming
Making use of \({{\partial CS_{A} } \mathord{\left/ {\vphantom {{\partial CS_{A} } {\partial G_{A} }}} \right. \kern-0pt} {\partial G_{A} }}\) in (14) and \({{\partial PS_{A} } \mathord{\left/ {\vphantom {{\partial PS_{A} } {\partial G_{A} }}} \right. \kern-0pt} {\partial G_{A} }}\) in (15), the effect of country A’s arming on its aggregate payoff is calculated as follows:
The above derivative can further be re-written as \(\frac{{\partial \varPi_{A} }}{{\partial G_{A} }} = E_{X} \frac{{\partial P_{X} }}{{\partial G_{A} }} + M_{Y} \left( { - \frac{{\partial P_{Y} }}{{\partial G_{A} }}} \right) + P_{X} \frac{{\partial X_{A} }}{{\partial G_{A} }}.\) Similarly, country B determines an arming allocation \(G_{B}\) that solves the following maximization problem: \(\mathop {\text{Max}}\limits_{{\{ G_{B} \} }} \varPi_{B} = CS_{B} + PS_{B} ,\) where \(CS_{B}\) and \(PS_{B}\) are consumer and producer surplus as given in Appendix 1. We decompose the effect of country B’s arming into three separate terms:
where \(E_{Y} \equiv (Y_{B} - D_{Y} )\) is the amount of the final good Y exported from B to A.
Alternatively, we can use (14)–(16) to decompose the effect of country A’s arming into three separate terms explicitly in terms of \(G_{A}\) and \(G_{B}\) as follows:
where \(X_{A} ,\)\(D_{X} ,\)\(M_{Y} ,\) and \(P_{X}\) are functions of \(G_{A}\) and \(G_{B} .\) That expression implies that country A increases its arming up to where marginal benefit equals marginal cost, that is,
As for country B, we have the following FOC:
Country B’s arming likewise is chosen where marginal benefit equals marginal cost, namely,
1.3 Appendix 3: Proof of Lemma 1
For country A, \({{\partial \varPi_{A} } \mathord{\left/ {\vphantom {{\partial \varPi_{A} } {\partial G_{A} }}} \right. \kern-0pt} {\partial G_{A} }} < 0\) when \(E_{X} ({{\partial P_{X} } \mathord{\left/ {\vphantom {{\partial P_{X} } {\partial G_{A} }}} \right. \kern-0pt} {\partial G_{A} }})\) is less than the sum of \(M_{Y} ( - {{\partial P_{Y} } \mathord{\left/ {\vphantom {{\partial P_{Y} } {\partial G_{A} }}} \right. \kern-0pt} {\partial G_{A} }})\) and \(P_{X} ({{\partial X_{A} } \mathord{\left/ {\vphantom {{\partial X_{A} } {\partial G_{A} }}} \right. \kern-0pt} {\partial G_{A} }})\) in absolute value. That is, \(MR_{A}^{Arms} < MC_{A}^{Arms} .\) Similarly, \({{\partial \varPi_{B} } \mathord{\left/ {\vphantom {{\partial \varPi_{B} } {\partial G_{B} }}} \right. \kern-0pt} {\partial G_{B} }} < 0\) when \(MR_{B}^{Arms} < MC_{B}^{Arms} .\) As a result, we have \(G_{A} = G_{B} = 0.\)□
1.4 Appendix 4: Comparative statics of the equilibrium arming under symmetry
Taking the derivative of \(G^{ * }\) (18) with respect to \(Z\), R, and t, respectively, we have the following derivatives:
1.5 Appendix 5: Aggregate payoff functions under asymmetry in national endowments
Substituting \(R_{A} = (R_{o} + \delta )\) and \(R_{B} = (R_{o} - \delta )\) into (28) and (29) in Appendix 1, we have the following aggregate payoff functions for countries A and B:
and
Rights and permissions
About this article
Cite this article
Chang, YM., Sellak, M. A game-theoretic analysis of international trade and political conflict over external territories. Public Choice 179, 209–228 (2019). https://doi.org/10.1007/s11127-018-0505-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11127-018-0505-9