Model averaging estimators for the stochastic frontier model

Abstract

Model uncertainty is a prominent feature in many applied settings. This is certainty true in the efficiency analysis realm where concerns over the proper distributional specification of the error components of a stochastic frontier model is, generally, still open along with which variables influence inefficiency. Given the concern over the impact that model uncertainty is likely to have on the stochastic frontier model in practice, the present research proposes two distinct model averaging estimators, one which averages over nested classes of inefficiency distributions and another that has the ability to average over distinct distributions of inefficiency. Both of these estimators are shown to produce optimal weights when the aim is to uncover conditional inefficiency at the firm level. We study the finite-sample performance of the model average estimator via Monte Carlo experiments and compare with traditional model averaging estimators based on weights constructed from model selection criteria and present a short empirical application.

Appendices

Appendices

A.1. Proof of Theorem 1. We first decompose C(w) as follows:

$$\begin{array}{c}C({\boldsymbol{w}}) = \left\Vert {\widehat {\boldsymbol{\rho }}({\boldsymbol{w}}) - \widehat {\boldsymbol{\rho }}_{{\mathrm{full}}}} \right\Vert^2\, + \,n^{1/2}\log (n){\boldsymbol{k}}\prime {\boldsymbol{w}}\\ = \left\Vert {\widehat {\boldsymbol{\rho }}({\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\Vert^2\, + \,\left\Vert {\widehat {\boldsymbol{\rho }}_{{\mathrm{full}}} - {\boldsymbol{\rho }}} \right\Vert^2 - 2\left\{ {\widehat {\boldsymbol{\rho }}({\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\}\prime \left\{ {\widehat {\boldsymbol{\rho }}_{{\mathrm{full}}} - {\boldsymbol{\rho }}} \right\} \\+\,n^{1/2}\log (n){\boldsymbol{k}}\prime {\boldsymbol{w}}.\end{array}$$

(A.1)

From the $\sqrt n$-consistency property of MLE and Assumption C.1, we have, for any $s^ \ast \in \{ {\cal O} \cup \{ t\} \}$,

$$\left\Vert {\widehat {\boldsymbol{\rho }}_{s^ \ast } - {\boldsymbol{\rho }}} \right\Vert^2 = \mathop {\sum}\limits_{i = 1}^n {\left\Vert {\frac{{\partial \widehat {\boldsymbol{\rho }}_{s^ \ast ,i}}}{{\partial \widehat {\boldsymbol{\theta }}_{s^ \ast }^\prime }}\mid _{\widehat {\boldsymbol{\theta }}_{s^ \ast } = \widetilde {\boldsymbol{\theta }}_{s^ \ast ,i}}(\widehat {\boldsymbol{\theta }}_{s^ \ast } - {\boldsymbol{\theta }}_{s^ \ast })} \right\Vert^2} = O_p(1),$$

(A.2)

where $\widetilde {\boldsymbol{\theta }}_{s^ \ast ,i}$ lies between $\widehat {\boldsymbol{\theta }}_{s^ \ast }$ and ${\boldsymbol{\theta }}_{s^ \ast }$. By the definition of $\widehat {\boldsymbol{w}}$ in Eq. (14), we have

$$\begin{array}{c}C(\widehat {\boldsymbol{w}}) \le \left\Vert {\widehat {\boldsymbol{\rho }}_{s^ \ast } - \widehat {\boldsymbol{\rho }}_{{\mathrm{full}}}} \right\Vert^2\, + \,n^{1/2}\log(n)k_{s^ \ast }\\ \le 2\left\Vert {\widehat {\boldsymbol{\rho }}_{s^ \ast } - {\boldsymbol{\rho }}} \right\Vert^2\, + \,2\left\Vert {\widehat {\boldsymbol{\rho }}_{{\mathrm{full}}} - {\boldsymbol{\rho }}} \right\Vert^2\, + \,n^{1/2}\log(n)k_{s^ \ast },\end{array}$$

(A.3)

which, along with (A.1), implies that

$$\begin{array}{lcc}\left\Vert {\widehat {\boldsymbol{\rho }}(\widehat {\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\Vert^2 - 2\left\{ {\widehat {\boldsymbol{\rho }}(\widehat {\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\}^{\prime} \left\{ {\widehat {\boldsymbol{\rho }}_{{\mathrm{full}}} - {\boldsymbol{\rho }}} \right\} \le 2\left\Vert {\widehat {\boldsymbol{\rho }}_{s^ \ast } - {\boldsymbol{\rho }}} \right\Vert^2\\ +\, \left\Vert {\widehat {\boldsymbol{\rho }}_{{\mathrm{full}}} - {\boldsymbol{\rho }}} \right\Vert^2\, + \,O(n^{1/2}\log(n))\end{array},$$

and thus

$$\begin{array}{lcc}\left\Vert {\widehat {\boldsymbol{\rho }}(\widehat {\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\Vert^2\, \le 2\left\Vert {\widehat {\boldsymbol{\rho }}_{s^ \ast } - {\boldsymbol{\rho }}} \right\Vert^2\, + \,\left\Vert {\widehat {\boldsymbol{\rho }}_{{\mathrm{full}}} - {\boldsymbol{\rho }}} \right\Vert^2 \\\,+ \,O(n^{1/2}\log(n)) + 2\left\Vert {\widehat {\boldsymbol{\rho }}(\widehat {\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\Vert\left\Vert {\widehat {\boldsymbol{\rho }}_{{\mathrm{full}}} - {\boldsymbol{\rho }}} \right\Vert\end{array}.$$

Therefore,

$$\begin{array}{lcc}\left\{ {\left\Vert {\widehat {\boldsymbol{\rho }}(\widehat {\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\Vert - \left\Vert {\widehat {\boldsymbol{\rho }}_{{\mathrm{full}}} - {\boldsymbol{\rho }}} \right\Vert} \right\}^2\, \le 2\left\Vert {\widehat {\boldsymbol{\rho }}_{s^ \ast } - {\boldsymbol{\rho }}} \right\Vert^2 \\+ \,O(n^{1/2}\log(n)) + 2\left\Vert {\widehat {\boldsymbol{\rho }}_{{\mathrm{full}}} - {\boldsymbol{\rho }}} \right\Vert^2\end{array}.$$

(A.4)

The full model belongs to ${\cal O}_1$ provided that any one candidate model belongs to ${\cal O}_1$. Hence we can obtain Eq. (15) from (A.2) and (A.4).

We next prove Eq. (16). Let

$$a_{s,m} = \left( {\widehat {\boldsymbol{\rho }}_s - \widehat {\boldsymbol{\rho }}_{{\mathrm{full}}}} \right)\prime \left( {\widehat {\boldsymbol{\rho }}_m - \widehat {\boldsymbol{\rho }}_{{\mathrm{full}}}} \right)$$

(A.5)

and Φ be an S × S matrix with its smth element given by

$$\Phi _{s,m} = a_{s,m} + n^{1/2}\log (n)(k_s + k_m)/2.$$

(A.6)

It can be easily shown that for any ${\boldsymbol{w}} \in {\cal W}$, C(w) = w′Φw. Now, define

$$\widetilde{\boldsymbol{w}} = \left({\widehat{w}}_1, \ldots, {\widehat{w}}_{s_o - 1},{\widehat{w}}_{s_o} + {\widehat{w}}_{m^ \ast }, {\widehat{w}}_{s_o + 1}, \ldots ,{\widehat{w}}_{m^ \ast - 1},0,{\widehat{w}}_{m^ \ast + 1}, \ldots ,{\widehat{w}}_S\right){\prime}.$$

Then we have

$$\begin{array}{c}0 \le C(\widetilde {\boldsymbol{w}}) - C(\widehat {\boldsymbol{w}})\\ = \widetilde {\boldsymbol{w}}\prime \Phi \widetilde {\boldsymbol{w}} - \widehat {\boldsymbol{w}}\prime {\bf{\Phi }}\widehat {\boldsymbol{w}}\\ = \left( {\widetilde {\boldsymbol{w}} + \widehat {\boldsymbol{w}}} \right)\prime {\bf{\Phi }}(\widetilde {\boldsymbol{w}} - \widehat {\boldsymbol{w}})\\ = \{ 2\widehat {\boldsymbol{w}}\prime - (0, \ldots ,0,\widehat w_{m^ \ast },0, \ldots ,0, - \widehat w_{m^ \ast },0, \ldots ,0)\} {\bf{\Phi }}\left( {0, \ldots ,0,\widehat w_{m^ \ast },0, \ldots ,0, - \widehat w_{m^ \ast },0, \ldots ,0} \right)\prime \\ = \widehat w_{m^ \ast }^2(2\Phi _{s_o,m^ \ast } - \Phi _{s_o,s_o} - \Phi _{m^ \ast ,m^ \ast }) + 2\widehat {\boldsymbol{w}}\prime {\bf{\Phi }}\left( {0, \ldots ,0,\widehat w_{m^ \ast },0, \ldots ,0, - \widehat w_{m^ \ast },0, \ldots ,0} \right)\prime \\ = \widehat w_{m^ \ast }^2(2\Phi _{s_o,m^ \ast } - \Phi _{s_o,s_o} - \Phi _{m^ \ast ,m^ \ast }) + 2\widehat w_{m^ \ast }\widehat {\boldsymbol{w}}\prime \left( {\Phi _{1,s_o} - \Phi _{1,m^ \ast }, \ldots ,\Phi _{S,s_o} - \Phi _{S,m^ \ast }} \right)\prime \\ = \widehat w_{m^ \ast }^2(2\Phi _{s_o,m^ \ast } - \Phi _{s_o,s_o} - \Phi _{m^ \ast ,m^ \ast }) + 2\widehat w_{m^ \ast }\mathop {\sum}\limits_{s = 1}^s {\widehat w_s} (\Phi _{s,s_o} - \Phi _{s,m^ \ast })\\ = \widehat w_{m^ \ast }^2O_p(1) + 2\widehat w_{m^ \ast }\mathop {\sum}\limits_{s = 1}^S {\widehat w_s} \left\{ {O_p(n^{1/2}) + n^{1/2}\log(n)(k_{s_o} - k_{m^ \ast })/2} \right\}\\ = \widehat w_{m^ \ast }^2O_p(1) + 2\widehat w_{m^ \ast }O_p(n^{1/2}) + 2\widehat w_{m^ \ast }n^{1/2}\log(n)(k_{s_o} - k_{m^ \ast })/2,\end{array}$$

where the seventh equality expression is obtained using (A.2), (A.5) and (A.6). This yields

$$\widehat {w}_{m^ {\ast} }n^{1/2}\log(n)(k_{m^ {\ast} } - k_{s_o})/2 \le \widehat {w}_{m^ \ast }^2O_p(1) + \widehat {w}_{m^ {\ast} }O_p(n^{1/2})$$

and hence $\widehat w_{m^ \ast } = O_p(\log ^{ - 1}(n))$, which is Eq. (16).

A.2. Proof of Theorem 2. Write

$$\begin{array}{c}\left\Vert {\widehat {\boldsymbol{\rho }}({\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\Vert^2\, =\left\Vert {\widehat {\boldsymbol{\rho }}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\Vert^2\, + \,\left\Vert {\widehat {\boldsymbol{\rho }}({\boldsymbol{w}}) - \widehat {\boldsymbol{\rho }}^ \ast ({\boldsymbol{w}})} \right\Vert^2\\ \qquad\qquad\qquad+ \;2\left\{ {\widehat {\boldsymbol{\rho }}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\}\prime \left\{ {\widehat {\boldsymbol{\rho }}({\mathbf{w}}) - \widehat {\boldsymbol{\rho }}^ \ast ({\mathbf{w}})} \right\}.\end{array}$$

(A.7)

From (A.1), (A.7), Assumption C.2, and the proof of Theorem 1′ in Wan et al. (2010), Theorem 2 holds provided that the following conditions hold:

$$\mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \frac{{\left\Vert {\widehat {\boldsymbol{\rho }}({\boldsymbol{w}}) - \widehat {\boldsymbol{\rho }}^ \ast ({\boldsymbol{w}})} \right\Vert^2}}{{\left\Vert {\widehat {\boldsymbol{\rho }}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\Vert^2}}\, = o_p(1),$$

(A.8)

$$\mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \frac{{\left| {\left\{ {\widehat {\boldsymbol{\rho }}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\}^\prime \left\{ {\widehat {\boldsymbol{\rho }}({\boldsymbol{w}}) - \widehat {\boldsymbol{\rho }}^ \ast ({\boldsymbol{w}})} \right\}} \right|}}{{\left\Vert {\widehat {\boldsymbol{\rho }}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\Vert^2}}\, = o_p(1),$$

(A.9)

and

$$\mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \frac{{\left| {\left\{ {\widehat {\boldsymbol{\rho }}({\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\}^\prime \left\{ {\widehat {\boldsymbol{\rho }}_{{\mathrm{full}}} - {\boldsymbol{\rho }}} \right\}} \right|}}{{\left\Vert {\widehat {\boldsymbol{\rho }}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{\rho }}} \right\Vert^2}} = o_p(1).$$

(A.10)

From Eq. (17) and Assumption C.1, we have

$$\begin{array}{l}\mathop {\sup}\limits_{{\boldsymbol{w}} \in {\cal W}} \frac{{\left\Vert {\widehat {\boldsymbol{\rho }}({\boldsymbol{w}})\, - \,\widehat {\boldsymbol{\rho }}^ {\ast} ({\boldsymbol{w}})} \right\Vert^{2}}}{{\left\Vert {\widehat {\boldsymbol{\rho }}^ \ast ({\boldsymbol{w}}) - \,{\boldsymbol{\rho }}} \right\Vert^{2}}}\\{\le} \xi _n^{ - 1}\mathop {\sum}\limits_{i = 1}^{n} {\mathop {\sup}\limits_{{\boldsymbol{w}} \in {\cal W}} } \left\{ {\widehat \rho _i({\boldsymbol{w}}) - \widehat \rho _i^ {\ast} ({\boldsymbol{w}})} \right\}^{2}\\ = \xi _n^{ - 1}\mathop {\sum}\limits_{i = 1}^{n} {\mathop {\sup}\limits_{{\boldsymbol{w}} \in {\cal W}} } \left\{ {\mathop {\sum}\limits_{s = 1}^{S} {w_s} (\widehat \rho _{s,i} - \widehat \rho _{s,i}^{\ast} )} \right\}^{2}\\ \le \xi _n^{ - 1}\mathop {\sum}\limits_{i = 1}^{n} {\mathop {sup}\limits_{1 \le s \le S} } (\widehat \rho _{s,i} - \widehat \rho _{s,i}^{\ast})^{2}\\ = \xi _{n}^{ - 1}\mathop {\sum}\limits_{i = 1}^{n} {\mathop {\sup}\limits_{1 \le s \le S} } \left\{ {\frac{{\partial \widehat \rho _{s,i}}}{{\partial \widehat {\boldsymbol{\theta }}_s{\prime} }}|_{\widehat {\boldsymbol{\theta }}_s = \widetilde {\boldsymbol{\theta }}_{s,i}}(\widehat {\boldsymbol{\theta }}_s - {\boldsymbol{\theta }}_s^{\ast} )} \right\}^{2}\\ = O_p(\xi _n^{ - 1}).\end{array}$$

(A.11)

It follows from (A.11) and Assumption C.2 that (A.8) holds. In a similar way, we can prove that (A.9) and (A.10) hold. This proves Theorem 2.

A.3. Proof of Theorem 3. It can be seen that

$$\begin{array}{c}CV_J({\boldsymbol{w}}) = \left\Vert {\widetilde {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{y}}} \right\Vert^2\\ = \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}} + \widetilde {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - (\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})) + {\boldsymbol{b}} - {\boldsymbol{y}}} \right\Vert^2\\ \le \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2 + \left\Vert {\widetilde {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert^2 + \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert^2 + \left\Vert {{\boldsymbol{b}} - {\boldsymbol{y}}} \right\Vert^2\\ + \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert\left\Vert {\widetilde {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert + \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert\left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert + \left| {(\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}){\prime}({\boldsymbol{b}} - {\boldsymbol{y}})} \right|\\ + \left\Vert {\widetilde {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert + \left\Vert {\widetilde {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\left\Vert {{\boldsymbol{b}} - {\boldsymbol{y}}} \right\Vert + \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\left\Vert {{\boldsymbol{b}} - {\boldsymbol{y}}} \right\Vert\\ \le \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2 + \left\Vert {\widetilde {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert^2 + \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert^2\\ + \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\left\Vert {\widetilde {\boldsymbol{b}}({\mathbf{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert + \left\Vert {{\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert\left\Vert {\widetilde {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\\ + \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert + \left\Vert {{\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert\left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\\ + \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\left\Vert {{\boldsymbol{b}} - {\boldsymbol{y}}} \right\Vert + \left| {({\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}){\prime}({\boldsymbol{b}} - {\boldsymbol{y}})} \right| + \left\Vert {\widetilde {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\\ + \left\Vert {\widetilde {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\left\Vert {{\boldsymbol{b}} - {\boldsymbol{y}}} \right\Vert + \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert\left\Vert {{\boldsymbol{b}} - {\boldsymbol{y}}} \right\Vert + \left\Vert {{\boldsymbol{b}} - {\boldsymbol{y}}} \right\Vert^2\\ \equiv \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2 + {\Pi}_n({\boldsymbol{w}}) + \left\Vert {{\boldsymbol{b}} - {\boldsymbol{y}}} \right\Vert^2\end{array}$$

and

$$\begin{array}{c}\left\Vert \,{\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2 = \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) + {\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2\\ = \left\Vert {{\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2 + \left\Vert \,{\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert^2 + \,2\left( {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right)\prime ({\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}})\\ = \left\Vert {{\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2 + \,\Xi _n({\boldsymbol{w}}).\end{array}$$

Hence to prove Theorem 3, it suffices to show that

$$\mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \frac{{\Xi _n({\boldsymbol{w}})}}{{\left\Vert {{\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2}} = o_p(1)$$

(A.12)

and

$$\mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \frac{{{\Pi}_n({\boldsymbol{w}})}}{{\left\Vert {{\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2}}\, = o_p(1).$$

(A.13)

Similar to the proof of (A.2), by Eq. (17) and Assumption C.4, we have

$$\begin{array}{l}\mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert^2\, = O_p(1)\quad \\{\mathrm{and}}\\ \mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \left\Vert {\widetilde {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert^2\, = O_p(1)\end{array}.$$

(A.14)

It is readily seen that

$$\left\Vert {{\boldsymbol{b}} - {\boldsymbol{y}}} \right\Vert^2\, = O_p(n)$$

(A.15)

and

$$\mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \frac{{\left\Vert {{\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert\left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert}}{{\left\Vert {{\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2}}, = \mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \frac{{\left\Vert {\widehat {\boldsymbol{b}}({\boldsymbol{w}}) - {\boldsymbol{b}}^ \ast ({\boldsymbol{w}})} \right\Vert}}{{\left\Vert {{\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert}}.$$

(A.16)

For any δ > 0,

$$\begin{array}{l}Pr\{ \mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \zeta _n^{ - 1}|({\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}){\prime}({\boldsymbol{b}} - {\boldsymbol{y}})| \,{>}\, \delta \} \\ \le Pr\{ \mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \zeta _n^{ - 1}\mathop {\sum}\limits_{s = 1}^S {w_s} |({\boldsymbol{b}}_m^ \ast - {\boldsymbol{b}}){\prime}({\boldsymbol{b}} - {\boldsymbol{y}})| \,{>}\, \delta \} \\ = Pr\{ \mathop {{\max }}\limits_s |({\boldsymbol{b}}_s^ \ast - {\boldsymbol{b}}){\prime}({\boldsymbol{b}} - {\boldsymbol{y}})| \,{>}\, \zeta _n\delta \} \\ \le \mathop {\sum}\limits_{s = 1}^S {Pr} \{ |({\boldsymbol{b}}_s^ \ast - {\boldsymbol{b}}){\prime}({\boldsymbol{b}} - {\boldsymbol{y}})| \,{>}\, \zeta _n\delta \} \\ \le \mathop {\sum}\limits_{s = 1}^S E \{ \zeta _n^{ - 2}\delta ^{ - 2}({\boldsymbol{b}}_s^ \ast - {\boldsymbol{b}}){\prime}({\boldsymbol{b}} - {\boldsymbol{y}})\} ^2\\ = \mathop {\sum}\limits_{s = 1}^S E \left[ {E\{ \zeta _n^{ - 2}\delta ^{ - 2}({\boldsymbol{b}}_s^ \ast - {\boldsymbol{b}}){\prime}({\boldsymbol{b}} - {\boldsymbol{y}})|{\boldsymbol{x}},{\boldsymbol{z}}\} ^2} \right]\\ = \mathop {\sum}\limits_{s = 1}^S E \left[ {\zeta _n^{ - 2}\delta ^{ - 2}({\boldsymbol{b}}_s^ \ast - {\boldsymbol{b}}){\prime}{\mathrm{var}}({\boldsymbol{b}} - {\boldsymbol{y}}|{\boldsymbol{x}},{\boldsymbol{z}})({\boldsymbol{b}}_s^ \ast - {\boldsymbol{b}})} \right]\\ \le \mathop {\sum}\limits_{s = 1}^S E \left[ {\zeta _n^{ - 2}\delta ^{ - 2}\sigma ^2\left\Vert {{\boldsymbol{b}}_s^ \ast - {\boldsymbol{b}}} \right\Vert^2} \right],\end{array}$$

where x = (x₁, …, x_n)′ and z = (z₁, …, z_n)′, and σ² is defined in the line above Assumption C.3. Together with Assumption C.3, this implies

$$\mathop {{\sup }}\limits_{{\boldsymbol{w}} \in {\cal W}} \frac{{|({\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}){\prime}({\boldsymbol{b}} - {\boldsymbol{y}})|}}{{\left\Vert {{\boldsymbol{b}}^ \ast ({\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2}} = o_p(1).$$

(A.17)

By combining (A.14)–(A.17) and Assumption C.3, we can obtain (A.12) and (A.13) and hence Eq. (21). This completes the proof of Theorem 3.

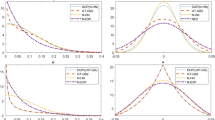
A.4. Simulation Results with Smaller Hold Out Sample. Similar to Tables 2 and 4 presents the mean, median and standard deviation of $\left\Vert {{\boldsymbol{b}}(\widehat {\boldsymbol{w}}) - {\boldsymbol{b}}} \right\Vert^2/n_{}^{}$, where b = E[y|x, z], based on AIC and BIC model selection, as well as s-AIC and s-BIC model averaging, the full (correctly specified model) and two variants of JCVMA across 1000 replications. JCVMA1 uses ${\boldsymbol{b}}(\widehat {\boldsymbol{w}}) = \widehat {\boldsymbol{b}}(\widehat {\boldsymbol{w}})$, as defined in Eq. (11), the fitted values from S candidate models not using hold-out samples, while JCVMA2 uses ${\boldsymbol{b}}(\widehat {\boldsymbol{w}}) = \widetilde {\boldsymbol{b}}(\widehat {\boldsymbol{w}})$, as defined in Eq. (12), the leave-J-observations-out fitted values from the estimated models. Note that both JCVMA1 and JCVMA2 use the same weights, $\widehat {\boldsymbol{w}}$, obtained from Eq. (20), they just conduct the averaging over different sets of fitted values. For all the simulations we leave out 2.5% of the sample size for our hold out prediction (i.e., for n = 200, we hold out 5 observations at a time, for n = 400 we hold out 10 observations at a time, etc.).

Table 4 Simulation results for the JCVMA estimator—1000 simulations. Holdout sample is 2.5% of n

Several insights are immediate from Table 4 relative to the results from Table 2. JCVMA2 still outperforms JCVMA1. JCVMA2 always outperforms the other methods in terms of mean risk, and also has equal standard deviation of risk. Comparing mean and median risk, it does not appear that the size of the hold out sample has much effect on the performance of either of the JCVMA estimators.