Abstract
In this paper we examine wage dispersion in labor markets across currently employed workers. We argue that differences in the potential productivity of a match (typically assumed to be known in the previous literature) generates a surplus between the minimum wage the worker is willing to accept and the maximum wage the firm is willing to offer for the job. Existence of this surplus leads to wage dispersion due to negotiating over the amounts extracted by each agent. Our objective is to estimate the surplus extracted by each firm-worker pair and the effect of the net extracted surplus on the wage, for each firm-worker pair using the two-tier stochastic frontier model. An empirical application finds that, on average, firms paid workers less than their expected productivity. More specifically, at the mean, the net effect of productivity uncertainty leads to equilibrium wages which are 3.33% below the expected productivity of matches.
Similar content being viewed by others
Notes
It might be revealed at a later date or not revealed at all.
Given that we have a supply side dataset we leave the effects of firm type on uncertainty for future research.
For a current synopsis of the state of the literature see the special issue of the European Economic Review (2006) in honor of Dale Mortensen.
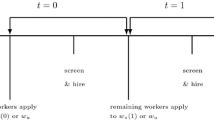
We thank an anonymous referee for suggesting the following framework to us.
Pissarides (2000) used p instead of \(\overline{wage}\) and rU instead of \(\underline{wage}\). Also, we used η to represent relative bargaining power of workers, instead of β as in Pissarides. Furthermore, in our modeling framework η can be observation specific.
The actual wage also represents a weighted average of the maximum offer and the reservation wage.
Using these notions we can define the expected productivity, μ(x) formally as the conditional expectation of wage given x when either there is no surplus to extract or surplus extracted by workers and firms are equal.
See Shapiro (2006) for a similar idea along these lines.
Although they did mention that the next logical step in their modelling framework would be to introduce human capital accumulation.
See Shi (2006) for a recent theoretical insight into the effects of productivity on wages.
We thank an anonymous referee for bringing this link with the model to our attention.
Although in (3) we are assuming μ(x) = x′δ thereby making the assumption that μ(x) is linear in parameters, the linearity assumption is not necessary for the frontier model to work. One can, in principle, assume any functional form on μ(x).
Recall that this is our measure of net surplus introduced prior.
Possibly from having relatively more bargaining power than firms.
Note that although E(u) and E(w) are non-zero, E(w − u) might be zero. If this happens then the OLS estimator of the intercept will also be unbiased. This, however, does not mean that surplus does not exist in the market.
Here Exp(σ z , σ 2 z ) denotes a random variable z that is exponentially distributed with mean σ z and variance σ 2 z .
The full derivations of all results are contained in the Appendix.
In fact, further research into the distributional assumptions of the two-tiered method, aside from making the technique more general, may also provide greater insight into wage variations once the error decomposition has taken place. See Tsionas (2008) for estimation of the two-tier model using Gamma distributions instead of exponentials. Also, the effect of distributional assumptions on the ranking of firms in efficiency studies has been found to have minor differences in the rankings of producers (see Kumbhakar and Lovell 2000, p. 90).
Calculations with a different data set, not reported here, suggest that there is an additional impact from being a new worker that lowers wages. The results are available upon request.
In their 1987 (1996) paper, Polachek and Yoon found that 79.8% (98.5%) of the unexplained wage variation was due to incomplete information.
If the goal is to obtain an estimate of the mean of the net effect, one can use the estimated value of E(w − u) = σ w − σ u which is −0.0339. This does not require use of the observation-specific estimates of w and u.
To avoid notational clutter we dropped the i subscript in all the derivations.
References
Abowd J, Kramarz F, Margolis D (1998) High wage workers and high wage firms. Econometrica 67:251–333
Acemoglu D (1999) Changes in unemployment and wage inequality: an alternative theory and some evidence. Am Econ Rev 89:1259–1278
Acemoglu D, Shimer R (2000) Wage and technology dispersion. Rev Econ Stud 67:585–607
Albrecht J, Axell B (1984) An equilibrium model of search employment. J Polit Econ 92:824–840
Blackburn M, Neumark D (1992) Unobserved ability, efficiency wages, and interindustry wage differentials. Q J Econ 107:1421–1436
Bontemps C, Robin J-M, Van den Berg GJ (1999a) An empirical equilibrium job search model with search on the job and heterogeneous workers and firms. Int Econ Rev 40:1039–1075
Bontemps C, Robin J-M, Van den Berg GJ (1999b) Equilibrium search with continuous productivity dispersion: theory and nonparametric estimation. Int Econ Rev 41:305–358
Bowlus A, Keifer N, Neumann G (1995) Estimation of equilibrium wage distributions with heterogeneity. J Appl Econ 10:S119–S131
Burdett K, Judd L (1983) Equilibrium price distributions. Econometrica 51:955–970
Burdett K, Mortensen D (1998) Wage differentials, employer size, and unemployment. Int Econ Rev 39:257–273
Burdett K, Vishwanath T (1988) Balanced matching and labor market equilibrium. J Polit Econ 96:1048–1065
Burdett K, Wright R (1998) Two-sided search and nontransferable utility. Rev Econ Dyn 1:220–245
Butters G (1977) Equilibrium distributions of sales and advertising prices. Rev Econ Stud 44:465–491
Cole H, Rogerson R (1999) Can the Mortensen-Pissarides matching model match the business-cycle facts? Int Econ Rev 40:933–959
Dey M, Flinn C (2005) An equilibrium model of health insurance provision and wage determination. Econometrica 73:571–627
Diamond P (1971) A model of price adjustment. J Econ Theory 3:156–168
Eckstein Z, Wolpin K (1990) Estimating a market equlibrium search model from panel data on individuals. Econometrica 58:783–808
Eckstein Z, Van den Berg G (forthcoming) Empirical labor search: a survey. J Econom
Flinn C (1986) Wage and job mobility of young workers. J Polit Econ S88–S110
Flinn C (2006) Minimum wage effects on labor market outcomes under search matching and endogenous contact rates. Econometrica 74:1013–1062
Flinn C, Heckman J (1982a) Models for the analysis of labor force dynamics. In: Rhodes G, Basmann R (eds) Advances in econometrics. JAI Press, London, CT
Flinn C, Heckman J (1982b) New methods for analyzing structural models of labor force dynamics. J Econom 18:115–168
Gaumont D, Schindler M, Wright R (2006) Alternative theories of wage dispersion. Eur Econ Rev 50:831–848
Hosios A (1990) On the efficiency of matching and related models of search and unemployment. Rev Econ Stud 57:279–298
Jondrow J, Lovell CAK, Materov IS, Schmidt P (1982) On the estimation of technical inefficiency in the stochastic frontier production function model. J Econom 19:233–38
Johnson W (1978) A theory of job shopping. Q J Econ 92:261–278
Jovanovic B (1979a) Firm specific capital and turnover. J Polit Econ 87:1246–1260
Jovanovic B (1979b) Job matching and the theory of turnover. J Polit Econ 87:972–990
Kumbhakar SC, Lovell CAK (2000) Stochastic frontier analysis. Cambridge University Press, New York.
Lippman S, McCall J (1976) The economics of job search: a survey, Part I. Econ Inq 14:155–189
Marimon R, Zilibotti F (1999) Unemployment vs. mismatch of talent: reconsidering unemployment benefits. Econ J 109:266–291
Meeusen W, van den Broeck J (1977) Efficiency estimation from Cobb-Douglas production functions with composed error. Int Econ Rev 18:435–444
Mortensen D, Pissarides C (1994) Job creation and job destruction in the theory of unemployment. Rev Econ Stud 61:397–415
Nagypál É (2004) Learning-by-doing versus learning about match quality: can we tell them apart? Northwestern University, Mimeo
Nelson P (1970) Information and consumer behavior. J Polit Econ 78(2):311–329
Osbourne MJ, Rubinstein A (1990) Bargaining and markets. Academic Press, San Diego
Pissarides CA (2000) Equilibrium unemployment theory. 2nd edn, MIT Press, Cambridge
Polachek S, Yoon BJ (1987) A two-tiered earnings frontier estimation of employer and employee information in the labor market. Rev Econ Stat 69:296–302
Polachek S, Yoon BJ (1996) Panel estimates of a two-tiered earnings frontier. J Appl Econ 11:169–178
Postel-Vinay F, Robin J-M (2002) Equilibrium wage dispersion with heterogeneous workers and firms. Econometrica 70:2295–2350
Postel-Vinay F, Robin J-M (2003) The distribution of earnings in an equilibrium search model with state-dependent offers and counter-offers. Int Econ Rev 43:989–1016
Pries M (2004) Persistence of employment fluctuations: a model of recurring job loss. Rev Econ Stud 71:193–215
Rothschild M (1973) Models of market organization with imperfect information: a survey. J Polit Econ 81(6):1283–1308
Shapiro J (2006) Wage and effort dispersion. Econ Lett 92:163–169
Shi S (2006) Wage differentials, discrimination and efficiency. Eur Econ Rev 50:849–875
Tsionas EG (2008) Maximum likelihood estimation of non standard stochastic frontier models using the Fourier transform. Working paper, Athens University of Business and Economics
Viscusi WK (1979) Job hazards and worker quit rates: an analysis of adaptive worker behavior. Int Econ Rev 20(1):29–58
Viscusi WK (1980a) A theory of job shopping: a Bayesian perspective. Q J Econ 94(3):609–614
Viscusi WK (1980b) Sex differences in worker quitting. Rev Econ Stat 62(3):388–398
Viscusi WK (1980c) Self-selection, learning-induced quits, and the optimal wage structure. Int Econ Rev 21(3):529–546
Viscusi WK (1983) Employment relationships with joint employer and worker experimentation. Int Econ Rev 24(2):313–322
Wilde L (1980) An information-theoretic approach to job quits. In: Lippman S, McCall J (eds) Studies in the economics of search. Amsterdam, North Holland
Acknowledgements
The authors thank two anonymous referees, Suqin Ge, Christopher Hanes, Daniel Henderson, Nicolai Kuminoff, Xiang Lie, Knox Lovell, and Solomon Polachek. Comments and suggestions from seminar participants at Syracuse University and SMU as well as Sandra Ahearn’s help in proofreading the Appendix are gratefully acknowledged. The usual disclaimer applies.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Derivations of selected equations
DerivationFootnote 23 of Eq. 5:
Beginning with the definition of the composed error term ɛ1 = v − u, the marginal distribution of this is, following Kumbhakar and Lovell (2000),
The three component error may then be written as ɛ = ɛ1 + w, which implies that ɛ1 = ɛ − w, yielding the following joint distribution, \(g(\varepsilon,w)=g(\varepsilon_{1},w)\cdot \vert d\varepsilon_{1} /d\varepsilon\vert= g(\varepsilon_{1},w)=f(\varepsilon_{1})\cdot f(w)\). Upon integrating out w one obtains the marginal distribution of ɛ. This is done below.
where χ1 = Φ (b) + exp{α − a}Φ (β). Similarly,
where χ2 = Φ(β) + exp {a − α}Φ (b) = exp {a − α}χ1.
The derivation for E(w|ɛ) follows similarly as:
Thus,
Using integration by parts, we get
and using the change of variable, \(z=\frac{u}{\sigma_{v}} +\left(b+\sigma_{v} \left(1+\lambda \right)\right)\Rightarrow dz={du\mathord{\left/ {\vphantom {du \sigma_{v}}} \right. } \sigma_{v}}\), we have
For the derivation of Eq. 12 we follow the same procedure as follows:
Using integration by parts
Finally, using the change of variable, \(z=\frac{w}{\sigma_{v}} +\left(\beta+\sigma_{v}\left(1+\lambda \right)\right)\Rightarrow dz={dw\mathord{\left/ {\vphantom {dw \sigma_{v}}} \right. } \sigma_{v}} \), we have
Rights and permissions
About this article
Cite this article
Kumbhakar, S.C., Parmeter, C.F. The effects of match uncertainty and bargaining on labor market outcomes: evidence from firm and worker specific estimates. J Prod Anal 31, 1–14 (2009). https://doi.org/10.1007/s11123-008-0117-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11123-008-0117-3