1 Introduction

It is well known that the III-N semiconductor materials have a wurtzite crystal and a direct energy bandgap, better chemical resistance and wider operational temperature range. Therefore, the gallium nitride-based semiconductors have attracted much attention on light emitting devices (LED) Nakamura et al. (1995), laser diodes Nakamura et al. (1996), ultraviolet photodetector Su et al. (2002) and high power and high-electron-mobility-transistors (HEMTs)Park and Bayram (2016), Wu and Alamo (2016), Wang et al. (2012) over twenty years.

At room temperature, the bandgap energy of InGaN from 0.7 to 3.4 eV depends on composition. Its corresponding wavelength can vary from the ultraviolet (365 nm) to the near-infrared (1770 nm). Therefore, the photodetector can detect the different wavelength by adjusting the In component x of \(\hbox {In}_{x}\hbox {Ga}_{1-x}\hbox {N}\). Although the InGaN LED has been commercialized and the InGaN quantum well solar cells have been reported widely. However, only a few research groups concentrating on the InGaN-based ultraviolet photodetector. The InGaN p–i–n photodiode reported exhibit a responsivity of 0.037 A/W at 426 nm with zero-bias Berkman et al. (2008). The high peak responsivity reported for a photodetector with 0.206 A/W at wavelength of 380 nm Su et al. (2009). LU Yi-dan et al reported that an unit front-illuminated InGaN p–i–n ultraviolet photodetector displayed an unbiased responsivity of 0.22 A/W at 378 nm Lu et al. (2014). Moreover, there were papers studied on the InGaN photodetector by Silvaco TCAD.

In this paper, we fabricated the back-illuminated \(\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\) ultraviolet photodetectors. The electric filed and responsivity properties of the photodetectors will be simulated and discussed by Silvaco TCAD. Furthermore, we discussed about the SRH recombination lifetime, the thickness of p-GaN layer, i-InGaN layer, n-GaN layer, the extinction coefficient and the polarization intensity for affecting the responsivity of the photodetector in detail. It was found that the simulation results can verify the theoretical parameters impact on the photodetector performances and provide a powerful reference for designing feasibility of the detector.

2 Experimental and important parameters

2.1 Device fabrications

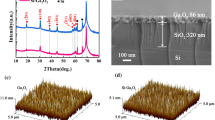
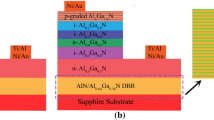
The \(\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\) epitaxial layers presented in this work were all grown on c-face (0001) double-sided polished sapphire substrates by Huazhong University of Science and Technology using a low-pressure metal organic chemical vapor deposition (MOCVD) system. In this experiment, trimethylindium (TMIn), trimethylgallium (TMGa) were used as sources of In and Ga, respectively, and nitrogen \((\hbox {N}_{2})\) were used as carrier gases. The Silane \((\hbox {SiH}_{4})\, (\hbox {Cp}_{2}\hbox {Mg})\) was used as the n-type sources and the biscyclopentadienyl magnesium was used as the p-type dopant, respectively. Here we designed two samples. The structure of sample 2 for fabricated back-illuminated \(\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\) photodetector p–i–n consist of a c-face (0001) sapphire substrate layer, a 1.5-μm-thick GaN buffer layer, a 2.8-μm-thick Si-doped n-GaN window layer, a 30-nm-thick undoped i-GaN layer, a 280-nm-thick undoped i-\(\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\) active layer, and a 230-nm-thick Mg-doped p-GaN layer. Yet the sample 1 has the same structure, except that without the 30-nm-thick i-GaN layer. Figure  1 shows the structures and SEM images of samples. It can be found that the interfaces were clearly indicated that epitaxial layers with high quality. The \(\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\) ultraviolet photodetectors were fabricated by the standard III–V group device fabrication processes by photolithography and inductively coupled plasma etching (ICP). The Ni/Au/Ni/Au (20/20/20/20 nm) and Ti/Al/Ti/Au (50/50/30/30 nm) was evaporated by electron-beam evaporation as p-type electrode and n-type electrode, respectively. The samples were annealed in RTP 500 rapid thermal annealing furnace after lift-off which was contributed to form the ohmic contact. Finally, a 300-nm-thick \(\hbox {SiO}_{2}\) layer was deposited via plasma-enhanced chemical vapor deposition (PECVD) for passivation.

Fig. 1
figure 1

The structures and SEM images of the samples. a Schematic diagrams of the samples, b SEM images of the samples

Full size image

2.2 Important parameters

The Silvaco TCAD is based on the a series of physical models for mathematical calculations. Those models consist of the fundamental physical equations which have been derived from the Maxwell’s laws and Poisson’s equation, the carrier continuity equations and the transport equations. In this study, we will use the carrier generation/recombination model, the carrier drift diffusion model, the bandgap narrowing model and the high/low field mobility model et al in the back-illuminated \(\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\) p–i–n ultraviolet photodetector simulation. For the \(\hbox {In}_{x}\hbox {Ga}_{1-x}\hbox {N}\) material, the bandgap energy obey to the Vgard’s Law SILVACO (2015) which is given by Eq. (1).

$$\begin{aligned} E_g \left( {In_x Ga_{1-x} N} \right) =xE_g \left( {InN} \right) +\left( {1-x} \right) E_g \left( {GaN} \right) -1.43x\left( {1-x} \right) \end{aligned}$$
(1)

Here, \(\hbox {E}_{g}\hbox {(InN)}\) and \(\hbox {E}_{g}\hbox {(GaN)}\) are the bandgap energy of InN and GaN at 300 k, \(\hbox {E}_{g}\hbox {(InN)}=0.7\, \hbox {eV}\), \(\hbox {E}_{g}\hbox {(GaN)}=3.4\, \hbox {eV}\), respectively.

The refractive index is a very important parameter that affects the photons absorption for the material. And for InGaN material, it can be expressed by the complex refractive index which is given by Eq. (2)

$$\begin{aligned} \tilde{n}=n+ik \end{aligned}$$
(2)

where n is the refractive index and k is the extinction coefficient. Using the Adachi’s refractive index model generally for the \(\hbox {In}_{x}\hbox {Ga}_{1-x}\hbox {N}\) material which is expressed by Eq. (3) Piprek (2003)

$$\begin{aligned} n_r \left( \nu \right) =\sqrt{A\left( \frac{h\nu }{E_g }\right) ^{-2}\left\{ {2-\sqrt{1+\frac{h\nu }{E_g }} -\sqrt{1-\frac{h\nu }{E_g }} } \right\} +B} \end{aligned}$$
(3)

where, \(E_g\) is the bandgap, \(\nu\) is the optical frequency of the incident photons and A, B are the material composition dependent parameters. The A and B parameters expressions are given by Eqs. (4) and (5)

$$\begin{aligned} A\left( x \right)= & {} 9.83\left( {1-x} \right) \text{+ }53.57x \end{aligned}$$
(4)
$$\begin{aligned} B\left( x \right)= & {} 2.74\left( {1-x} \right) -9.19x \end{aligned}$$
(5)

The extinction coefficient k can be obtained by the relationship with the absorption coefficient \(\alpha\) from Eq. (6).

$$\begin{aligned} \alpha =\frac{4\pi k}{\lambda } \end{aligned}$$
(6)

The absorption coefficient \(\alpha\) is expressed by Eq. (7) Brown et al. (2010).

$$\begin{aligned} \alpha \left( {hv} \right) =10^5\sqrt{a\left( {hv-E_g } \right) +b\left( {hv-E_g } \right) ^2} cm^{-1} \end{aligned}$$
(7)

where, a and b are the fitting parameters. For GaN, a is 3.52517, b is −0.65710 and for InN, a is 0.69642, b is 0.46055. The other values of a and b in composition fraction x range from 0 to 1 over scope of the whole \(\hbox {In}_{x}\hbox {Ga}_{1-x}\hbox {N}\) are obtained by linear interpolation, their values are shown in Table  1.

Table 1 The values of a and b in the \(\hbox {In}_{x}\hbox {Ga}_{1-x}\hbox {N}\) absorption coefficient model
Full size table

In the lattice mismatch between heterojunctions due to the different lattice constants produce spontaneous polarization and piezoelectric polarization. Those stresses create higher interface charges density at heterojunctions interface between InGaN/GaN layers. At the same times, the Vegard’s Law is used to calculate the interface charges for the spontaneous polarization and piezoelectric polarization intensity of the \(\hbox {In}_{x}\hbox {Ga}_{1-x}\hbox {N}\) material. The spontaneous polarization is caused by non-ideal symmetry of internal structural under no stress Ambacher et al. (2002). The spontaneous polarization of the \(\hbox {In}_{x}\hbox {Ga}_{1-x}\hbox {N}\) is a function of In composition fraction x given to second order in x which is expressed by Eq. (8).

$$\begin{aligned} P_{sp} \left( {In_x Ga_{1-x} N} \right) =-0.042x-0.034\left( {1-x} \right) +0.038x\left( {1-x} \right) \end{aligned}$$
(8)

The intensity of the piezoelectric polarization which results from the stress effect of the heterojunctions interface and the lattice constants mismatch Piprek (2007) can be expressed by Eq. (9).

$$\begin{aligned} P_{piezo} =\left( {1-R} \right) 2\frac{a-a_0 }{a_0 }\left[ {e_{31} -e_{33} \frac{C_{13} }{C_{33} }} \right] \end{aligned}$$
(9)

where, R is the strain relaxation degree, \(\hbox {a}_{0}\) is the substrate lattice constant, a is the epitaxial layer lattice constant, \(\hbox {e}_{33}\) and \(\hbox {e}_{31}\) are the piezoelectric constants, and \(\hbox {C}_{13}\) and \(\hbox {C}_{33}\) are the elastic constants. The total macroscopic polarization intensity P is the sum of the spontaneous polarization \(\hbox {P}_{sp}\) and the piezoelectric polarization \(\hbox {P}_{piezo}\) intensity that can be expressed as \(P = P_{sp} \text{+ }P_{piezo}\). The thin polarization-induced charges of the InGaN/GaN interface are equal to the polarized charges of the upper layer minus the polarized charges of the lower layer.

3 Results and discussion

Figure  2 shows the spectral responsivity of sample 1 and sample 2 at zero bias. The spectral responsivity was measured by a test system which was consists of a xenon lamp, a monochromator, and a computer-controlled SR570 current preamplifier. The light from Xenon lamp went-through the monochromator and then irradiated to the photodetector. The photodetector converted the incident light into the response current. The current was amplified by the SR570 and the current data was recorded by computer. In addition, the test responsivity must be calibrated by standard Si photodetector. The spectral responsivity of photodetectors was improved from 0.06 A/W at 394 nm of sample 1 to 0.19 A/W at 402 nm of sample 2. It was clear that the response band of sample 2 was larger than sample 1. The possible reason was that the In composition x was not well controlled under the growth process. According to long cutoff wavelength of the spectral responsivity can be calculated the In composition x of sample 1 is 0.09, the sample 2 is 0.14.

Fig. 2
figure 2

Sepctral responsivity of sample 1 and sample 2 at zero bias

Full size image
Fig. 3
figure 3

Dark current–voltage (I–V) characteristics of samples

Full size image

Figure  3 shows the dark current-voltage characteristics of InGaN photodetectors. The I–V measurements were carried out on a cascade probe station using a Keithley 236 semiconductor analyzer. The phototsensitive suface was circular with diameters of 40, 50 μm.The dark current of sample 2 was as low as 1 μA at reverse bias of −10 V, and dark current of sample 2 was much less than sample 1.

The back-illuminated InGaN p–i–n ultraviolet photodetector was simulated by Atlas module in Silvaco TCAD. For studying the factors that affect the responsivity of the InGaN photodetector, we have made a detail analysis of the sample 2 structure. Here, we have studied the SRH recombination lifetime, the thickness of n-GaN layer, i-InGaN layer and p-GaN layer, the extinction coefficient k and the polarization intensity, mainly.

The electric filed across the structure of the samples simulated by Silvaco TCAD, as shown in Fig.  4. It can be found that the electric filed at i-GaN/n-GaN interface of sample 2 was much smaller than sample 1 at the i-InGaN/n-GaN interface. The electric filed decreased from 0.375 MV/cm of sample 1 to 0.135 MV/cm of sample 2. One possible reason could be that the 30-nm-thick i-GaN increase the distance of build-in potential impact. In addition, the 30-nm-thick i-GaN layer can reduce the polarized charge density. If the relaxation degree R=0, the spontaneous polarization charge density of sample 1 was \(-0.0316\, \hbox {C/m}^2\) at \(\hbox {i-}\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\)/n-GaN interface. However, sample 2 spontaneous polarization charge density was \(-0.0305\, \hbox {C/m}^2\) at \(\hbox {i-In}_{0.14}\hbox {Ga}_{0.86}\hbox {N/i-GaN}\) interface. The polarized charge resulting in form a electron barrier and attract a large number of holes at interface to form an induced p–n junction. The direction of the electric field of the induced p–n junction was opposite to that of the original p–n junction. The photo-generate carriers were recombined by induced p–n junction. Therefore, the 30-nm-thick i-GaN growth between i-InGaN and n-GaN can increase responsivity. Wang et al. (2010) had demonstrated that decrease in the polarized charge density can increase the spectral responsivity.

Fig. 4
figure 4

Electric filed profile of sample 1 and sample 2

Full size image

Figure  5 shows the spectral responsivity of the sample 2 with different SRH recombination lifetime compare against the experimental values. It can be found that the biggest peak responsivity was 0.22 A/W at 398 nm when the SRH recombination lifetime was about 10 ns. Furthermore, the sample 2 was remained a high responsivity about 0.19 A/W at the wavelength of 380–425 nm. It was found that the simulation results were in good agreement with the experimental values when the SRH recombination lifetime about 0.01–0.1 ns. According to the formula between the diffusion length and the carrier lifetime, the diffusion distance of electrons and holes decreased with the decrease of the carrier recombination lifetime The peak responsivity was less than 0.10 A/W when the SRH recombination lifetime was 0.001 ns. Therefore, the number of carriers recombination increased and the number photo-generated of carriers decreased in the depletion region, which resulted in the responsivity decreased.

Fig. 5
figure 5

The spectral responsivity with different SRH carrier recombination lifetime and the experimental values

Full size image

Next, the spectral responsivity with different thickness of each layer of the back-illuminated p–i–n photodetector was studied. Figure  6 shows the responsivity spectral with different n-GaN thickness when the thickness of i-InGaN layer was 280 nm. It was noted that the responsivity of less than 398 nm was decreased with the thickness of n-GaN layer increased of the sample 2. As we know, the absorption edge of GaN layer was 365 nm. It means that the light of wavelength less than 365 nm was absorbed by n-GaN layer. It was found that the absorption length in n-GaN layer was less than 0.8 μm by calculating the absorption length relationship with wavelength. Therefore, the absorption length was less than 800 nm in the n-GaN layer for the wavelength of light less than 365 nm. In addition, the responsivity decreased with the increase of the n-GaN layer thickness at 365–398 nm. The ultraviolet light can’t be absorbed completely at 365–398 nm, which results in a small counts of photons absorbed by the depletion layer form a response signal directly. It was noted that increase of the n-GaN thickness caused the number of photons absorbed by the depletion layer to decrease so that the responsivity was decreased.

Fig. 6
figure 6

The spectral responsivity with different n-GaN thickness

Full size image

The appropriate thickness of intrinsic layer can be designed to achieve the optimal peak responsivity. The responsivity increased with the rise of thickness of i-InGaN layer in a certain range when the thickness of p-GaN layer and n-GaN layer unchanged, as shown in Fig.  7. Because that the depletion layer width would be increased with the thickness of i-InGaN layer, the effective working area of photoelectric conversion increased. It means that the number of photons absorbed increased with increase of i-InGaN layer, so the responsivity can be improved. However, it can be found that the responsivity was not obviously increased and saturated gradually when the thickness of i-InGaN layer was more than 400 nm.

Fig. 7
figure 7

The spectral responsivity with different i-InGaN thickness

Full size image
Fig. 8
figure 8

The electric field distribution with different i-InGaN thickness

Full size image

It was found that the electric field intensity decreased with the increase of i-InGaN layer. At the same time, the recombination probability of the photo-generated carriers was increased during drift process so that the device responsivity increased was not obvious. The responsivity was drop rapidly when the thickness of i-InGaN layer exceeds 800 nm. We can clearly explain those results in two reasons. First, the electric filed intensity was drastically decreased near the n-GaN side, as shown in Fig.  8, which leading to the drift velocity decreased drastically. The other one was the drift distance increasing with the increase of thickness of i-InGaN layer. These two reasons lead to increase of carrier recombination probability and decrease of responsivity. Furthermore, the resistance value of the device was increased with increase of the thickness of i-InGaN layer that results in the RC time constant increased and the response speed of the device decreased.

Fig. 9
figure 9

The spectral responsivity with different p-GaN thickness

Full size image

Figure  9 shows that the responsivity of the sample 2 with different p-GaN thickness. It can found that the responsivity was substantially independent of the thickness of p-GaN layer. The incident photons were almost completely absorbed by i-InGaN layer on the detector, no extra incident photons into the p-GaN layer to form the response signal.

Fig. 10
figure 10

The responsivity spectral of structure 2 with \(\hbox {i-}\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\), \(\hbox {i-In}_{0.14}\hbox {Ga}_{0.86}\hbox {N}\) and the experimental values

Full size image

The III-N materials have the different refractive index n and extinction coefficient k with different wavelength light. The refractive index n mainly affects the photons energy are less than the bandgap width that cannot be absorbed by the material, while the extinction coefficient k mainly affects the photons energy are greater than the bandgap width that can be absorbed. So the refractive index n parameter influence was much smaller than the extinction coefficient k on the responsivity. Therefore, determining the accurate extinction coefficient k was vital important for the device simulation by Silvaco TCAD calculation.

Wang et al. (2010) found that the crystalline quality and surface morphology of InGaN layer depredates with increasing thickness. Moreover, the InGaN layer strain relaxation and In components x increased with the increase of the thickness of InGaN layer. Figure  10 shows that responsivity spectral curves of structure 2 with \(\hbox {i-}\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\), \(\hbox {i-In}_{0.14}\hbox {Ga}_{0.86}\hbox {N}\) and the experimental results. It can be seen that the simulation results were in good agreement with the experimental result when In component x was introduced in a 0.05 increment as \(\hbox {i-In}_{0.14}\hbox {Ga}_{0.86}\hbox {N}\). It means that the InGaN layer strain relaxation has a great influence on the responsivity of p–i–n photodetector.

Fig. 11
figure 11

The effect of different polarization intensities on responsivity curves and electric field distributions

Full size image

Considering of the effect of strain relaxation on the materials, a thin charge layer was set up between i-InGaN layer and p-GaN layer to substitute for the polarized charges. Since the thickness of the intercalation layer was about 2 nm, the effect of ionization free carriers can be negligible on the whole device. Here, the polarization charge density can convert to the doping concentration of the intercalation layer, express by Eq. (10)

$$\begin{aligned} \delta N=\frac{Q}{V}=\frac{Q}{S\cdot d}=\frac{\sigma }{d} \end{aligned}$$
(10)

where, Q is the total amount of polarized charge, V is the volume of the intercalation layer, S, d are the intercalation layer area and thickness, \(\sigma\) is the polarized interface charge density.

The effect of different polarization intensities on the responsivity spectral of the back-illuminated p–i–n detector was shown in Fig.   11a. It was found that the polarization strength had little effect on the responsivity of the device. The intensity of the electric field increased with the strain relaxation degree R = 0 to R = 1 from \(0.13\, \hbox {MV/cm}\) to 0.15 MV/cm at the p-GaN/i-InGaN interface, as shown in Fig.  11b. Therefore, the total intensity of the depletion layer had little change, which had little effect on the photon absorption that the responsivity no change of the device.

4 Conclusion

In this paper, the back-illuminated \(\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\) p–i–n ultraviolet photodetector were fabricated by the standard III-V group device fabrication processes and simulated by the Atlas module of Silvaco TCAD semiconductor simulation software, responsively. The spectral responsivity of photodetector was improved from 0.06 A/W at 394 nm to 0.19 A/W at 402 nm achieves a high peak responsivity since growth of a 30-nm-thick i-GaN layer between the i-InGaN layer and the n-GaN layer. The responsivity characteristics of \(\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\) p–i–n ultraviolet photodetector were studied in detail. The simulation results reveal that the responsivity has great relationship with the SRH recombination carrier lifetime, intrinsic layer thickness and extinction coefficient k. Photo-response results indicate that polarization charge has little effect on the responsivity of the device because of the In composition x was only 0.09. Finally, when the In composition of InGaN introduced a 0.05 increment and the SRH recombination lifetime about 0.01–0.1 ns, the responsivity spectral was in good agreement with the experimental results in the back-illuminated \(\hbox {In}_{0.09}\hbox {Ga}_{0.91}\hbox {N}\) p–i–n ultraviolet photodetector.