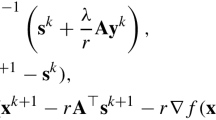Abstract
We present a primal-dual predictor-corrector interior-point method for symmetric cone optimization. The proposed algorithm is based on the Nesterov-Todd search directions and a wide neighborhood, which is an even wider neighborhood than a given negative infinity neighborhood. At each iteration, the method computes two corrector directions in addition to the Ai and Zhang directions (SIAM J. Optim. 16, 400–417, 2005), in order to improve performance. Moreover, we derive the complexity bound of the wide neighborhood predictor-corrector interior-point method for symmetric cone optimization that coincides with the currently best known theoretical complexity bounds for the short step algorithm. Finally, some numerical experiments are provided to reveal the effectiveness of the proposed method.
Similar content being viewed by others
References
Karmarkar, N.K.: A new polynomial-time algorithm for linear programming. Combinatorica 4, 373–395 (1984)
Faraut, J., Korányi, A.: Analysis on Symmetric Cones. Oxford University Press, New York (1994)
Schmieta, S.H., Alizadeh, F.: Extension of primal-dual interior-point algorithms to symmetric cones. Math. Program. 96, 409–438 (2003)
Gu, G., Zangiabadi, M., Roos, C.: Full Nesterov-Todd step interior-point methods for symmetric optimization. Eur. J. Oper. Res. 214, 473–484 (2011)
Zhang, J., Zhang, K.: Polynomiality complexity of an interior point algorithm with a second order corrector step for symmetric cone programming. Math. Meth. Oper. Res. 73, 75–90 (2011)
Liu, H., Yang, X., Liu, C.: A new wide neighborhood primal-dual infeasible-interior-point method for symmetric cone programming. J. Optim. Theory Appl. 158, 796–815 (2013)
Ai, W.: Neighborhood-following algorithms for linear programming. Sci. China Ser. A 47, 812–820 (2004)
Ai, W., Zhang, S.: An \(O(\sqrt {n}L)\) iteration primal-dual path-following method, based on wide neighborhoods and large updates, for monotone LCP. SIAM J. Optim. 16, 400–417 (2005)
Li, Y., Terlaky, T.: A new class of large neighborhood path-following interior point algorithms for semidefinite optimization with \(O(\sqrt {n}\log (Tr(X^{0} S^{0})/\varepsilon ))\) iteration complexity. SIAM J. Optim. 20, 2853–2875 (2010)
Feng, Z.Z.: A new \(O(\sqrt {n}L)\) iteration large update primal-dual interior-point method for second-order cone programming. Numer. Funct. Anal. Optim. 33, 397–414 (2012)
Feng, Z.Z., Fang, L.: A new \(O(\sqrt {n}L)\)-iteration predictor-corrector algorithm with wide neighborhood for semidefinite programming. J. Comp. App. Math. 256, 65–76 (2014)
Sayadi Shahraki, M., Mansouri, H., Zangiabadi, M.: A new primal-dual predictor-corrector interior-point method for linear programming based on a wide neighborhood. J. Optim. Theory Appl. https://doi.org/10.1007/s10957-016-0927-9 (2016)
Liu, C., Liu, H., Cong, W.: An \(O(\sqrt {n}L)\) iteration primal-dual second-order corrector algorithm for linear programming. Optim. Lett. 5, 729–743 (2011)
Sayadi Shahraki, M., Mansouri, H., Zangiabadi, M.: A new wide neighborhood primal-dual predictor-corrector interior-point method for linear programming. To appear in Numer. Funct. Anal. Optim. https://doi.org/10.1080/01630563.2016.1138128 (2015)
Nesterov, Y.E., Todd, M.J.: Primal-dual interior-point methods for self-scaled cones. SIAM J. Optim. 8, 324–364 (1998)
Faybusovich, L.: A Jordan-algebraic approach to potential-reduction algorithms. Math. Z. 239, 117–129 (2002)
Nesterov, Y.E., Nemirovskii, A.S.: Interior-Point Polynomial Algorithms in Convex Programming. SIAM, Philadelphia (1994)
Liu, C.: Study on Complexity of Some Interior-Point Algorithms in Conic Programming. Ph.D. thesis, Xidian University, in Chinese (2012)
Wright, S.J.: Primal-Dual Interior-Point Methods. SIAM, Philadelphia (1997)
Todd, M.J., Toh, K. C., Tautauncau, R.H.: On the Nesterov-Todd direction in semidefinite programming. Optimization 8, 769–796 (1998)
Liu, C., Liu, H., Liu, X.: Polynomial convergence of Second-Order Mehrotra-Type Predictor-Corrector algorithms over symmetric cones. J. Optim. Theory Appl. 154, 949–965 (2012)
Zhang, Y., Zhang, D.: On polynomial of the Mehrotra-type predictor-corrector interior-point algorithms. Math. Program. 68, 303–318 (1995)
Bai, Y.Q., Wang, G.Q., Roos, C.: Primal-dual interior-point algorithms for second-order cone optimization based on kernel functions. Nonlinear Anal. 70, 3584–3602 (2009)
Acknowledgements
The research of the first author was in part supported by a grant from IPM (No. 96900076). The second and third authors thank Shahrekord University and the fourth author thanks Research Council of Sharif University of Technology for financial support. The second and third authors were also partially supported by the Center of Excellence for Mathematics, University of Shahrekord, Shahrekord, Iran.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sayadi Shahraki, M., Mansouri, H., Zangiabadi, M. et al. A wide neighborhood primal-dual predictor-corrector interior-point method for symmetric cone optimization. Numer Algor 78, 535–552 (2018). https://doi.org/10.1007/s11075-017-0387-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-017-0387-9