Modal interactions in the nonlinear dynamics of a beam–cable–beam

Abstract

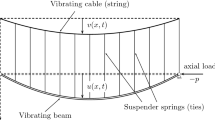
Quadratic and cubic modal interactions characterize the geometrically nonlinear dynamics of a parametric analytical model composed by two cantilever beams connected by a suspended shallow cable. The natural frequencies and modes of the linearized model are determined exactly, by solving the integral–differential eigenproblem governing the undamped free oscillations. Interesting phenomena of linear cable–beam interaction (frequency veering and modal hybridization) are recognized in the spectrum. Global and local modes are distinguished by virtue of the two localization factors measuring the modal kinetic energy stored in the beams and cable, respectively. The localization level is also put in relation to the magnitude of the quadratic and cubic nonlinearities. Therefore, the exact linear eigensolution is employed to formulate a nonlinearly coupled two-degrees-of-freedom model, defined in the reduced space of the modal amplitudes corresponding to a global and a local mode. The modal interactions between the two modes are analyzed, with focus on the autoparametric excitation mechanisms that can be favored by the occurrence of integer frequency ratios (1:2 and 2:1). Such internal resonance conditions enable significant transfers of mechanical energy—essentially governed by the quadratic coupling terms—from the small amplitudes of the externally excited global mode to the high amplitudes of the autoparametrically excited local mode. Different regimes of periodic and quasi-periodic oscillations are identified.

Appendix

The modal coefficients related to masses (set to unity by virtue of the mode normalization), dampings and external forces in the equations of motion (23) governing the reduced 1dof and 2dofs models are

$$\begin{aligned}&m_{\textit{ij}} = \frac{\beta _c^2 }{\omega ^{2}}I_{\textit{ij}}^c +\mu \alpha \chi \frac{\beta _{b1}^4 }{\omega ^{2}}I_{\textit{ij}}^{b1}+ \nonumber \\&\qquad +\mu \alpha \chi \frac{\beta _{b2}^4 }{\omega ^{2}}I_{\textit{ij}}^{b2} \nonumber \\&\zeta _{\textit{ij}} =\frac{2\xi _c }{\omega }I_{\textit{ij}}^c +\mu \alpha \chi \frac{2\xi _{b1} }{\omega }I_{\textit{ij}}^{b1}+ \nonumber \\&\qquad +\mu \alpha \chi \frac{2\xi _{b2} }{\omega }I_{\textit{ij}}^{b2}\nonumber \\&p_i \left( \tau \right) = f_c \left( \tau \right) F_{i}^c +\alpha f_{b1} \left( \tau \right) F_{i}^{b1}+ \nonumber \\&\qquad \qquad +\,\alpha f_{b2} \left( \tau \right) F_{i}^{b2} \end{aligned}$$

(A.1)

while the coefficients of the quadratic and cubic terms are defined as

$$\begin{aligned} c_{ij}^n= & {} \mu \left[ {\begin{array}{l} \left( {4\delta J_{ij}^n -\frac{1}{2}G_{ij}^n } \right) \left( {2-\delta _{ij} } \right) + \\ -C_{ij}^n -D_{ij}^n \left( {1-\delta _{ij} } \right) \\ \end{array}} \right] \nonumber \\ c_{\textit{ijh}}^n= & {} -\frac{1}{2}\mu \delta H_{ijh}^n \delta _{ij} +\nonumber \\&\quad -\left[ {\left( {\mu \delta Q_{\textit{ijh}}^n +\frac{1}{2}P_{\textit{ijh}}^n } \right) \left( {1-\delta _{\textit{ij}} } \right) } \right] \end{aligned}$$

(A.2)

where $\delta _{ij}$ is the Kronecker symbol, the superscript n is related to the mode (that is, $n=1$ and $n=2$ are referred to the first and second mode, respectively), while the subscript $i=1,2$, $j=1,2$ and $h=1,2$. The following positions have been introduced to enlighten the notation in the nonlinear equations of motion (23) governing the reduced 2dofs model

$$\begin{aligned}&c_{ij}^n \rightarrow c_{ij} \, \hbox {for} \,n=1\\&c_{ij}^n \rightarrow d_{ij} \, \hbox {for} \,n=2\\&c_{ijh}^n \rightarrow c_{ijh} \, \hbox {for} \,n=1\\&c_{ijh}^n \rightarrow d_{ijh} \, \hbox {for} \,n=2 \end{aligned}$$

The following integrals have been used in Eqs. (A.1) and (A.2)

$$\begin{aligned} I_{ij}^c= & {} \int _0^1 {\varphi _{ci} } \varphi _{cj} \mathrm{d}x_c \\ I_{ij}^{b1}= & {} \int _0^1 {\varphi _{b1i} } \varphi _{b1j} \mathrm{d}x_{b1} \\ I_{ij}^{b2}= & {} \int _0^1 {\varphi _{b2i} } \varphi _{b2j} \mathrm{d}x_{b2} \\ F_{i}^c= & {} \int _0^1 {\psi _{c} } \varphi _{cj} \mathrm{d}x_c \\ F_{i}^{b1}= & {} \int _0^1 {\psi _{b1} } \varphi _{b1i} \mathrm{d}x_{b1} \\ F_{i}^{b2}= & {} \int _0^1 {\psi _{b2} } \varphi _{b2i} \mathrm{d}x_{b2} \\ J_{ij}^n= & {} \int _0^1 {{\varphi }^{\prime }_{ci} } {\varphi }^{\prime }_{cj} \mathrm{d}x_c \int _0^1 {\varphi _{cn} } \mathrm{d}x_c \\ G_{ij}^n= & {} -\alpha _{b2} \varphi _{b2n} \left( 1 \right) \int _0^1 {{\varphi }^{\prime }_{ci} \varphi _{cj} } \mathrm{d}x_c + \\&+\,\alpha _{b1} \varphi _{b1n} \left( 1 \right) \int _0^1 {{\varphi }^{\prime }_{ci} \varphi _{cj} } \mathrm{d}x_c \\ C_{ij}^n= & {} \alpha _{b2} \varphi _{b2j} \left( 1 \right) \int _0^1 {{\varphi }^{\prime \prime }_{ci} \varphi _{cn} } \mathrm{d}x_c + \\&-\,\alpha _{b1} \varphi _{b1j} \left( 1 \right) \int _0^1 {{\varphi }^{\prime \prime }_{ci} \varphi _{cn} } \mathrm{d}x_c+ \nonumber \\&+\,8\delta \int _0^1 {\varphi _{cj} } \mathrm{d}x_c \int _0^1 {{\varphi }^{\prime \prime }_{ci} \varphi _{cn} } \mathrm{d}x_c \\ D_{ij}^n= & {} \alpha _{b2} \varphi _{b2i} \left( 1 \right) \int _0^1 {{\varphi }^{\prime \prime }_{cj} \varphi _{cn} } \mathrm{d}x_c - \\&-\,\alpha _{b1} \varphi _{b1i} \left( 1 \right) \int _0^1 {{\varphi }^{\prime \prime }_{cj} \varphi _{cn} } \mathrm{d}x_c+ \nonumber \\&+\,8\delta \int _0^1 {\varphi _{ci} } \mathrm{d}x_c \int _0^1 {{\varphi }^{\prime \prime }_{cj} \varphi _{cn} } \mathrm{d}x_c \\ H_{ijk}^n= & {} \int _0^1 {{\varphi }^{\prime }_{ci} {\varphi }^{\prime }_{cj} } \mathrm{d}x_c \int _0^1 {{\varphi }^{\prime \prime }_{ck} \varphi _{cn} } \mathrm{d}x_c \\ Q_{ijk}^n= & {} \int _0^1 {{\varphi }^{\prime }_{cj} {\varphi }^{\prime }_{ck} } \mathrm{d}x_c \int _0^1 {{\varphi }^{\prime \prime }_{ck} \varphi _{cn} } \mathrm{d}x_c \\ P_{ijk}^n= & {} \int _0^1 {\left( {{\varphi }^{\prime }_{ck} } \right) ^{2}} \mathrm{d}x_c \int _0^1 {{\varphi }^{\prime \prime }_{cj} \varphi _{cn} } \mathrm{d}x_c \end{aligned}$$

where the functions $\psi _c(x_c), \psi _{b1}(x_{b1}), \psi _{b2}(x_{b2})$ define the external loads $p_c(x_c, \tau )=f_c(\tau )\psi _c(x_c), p_{b1}(x_{b1},\tau )=f_{b1}(\tau )\psi _{b1}(x_{b1})$ and $p_{b2}(x_{b1},\tau )=f_{b2}(\tau )\psi _{b2}(x_{b2})$.