1 Introduction

Since its introduction into clinical practice 15 years ago, capsule endoscopy (CE) has become the primary modality for examining the surface lining of the small intestine, an anatomical site previously considered to be inaccessible to clinicians. However, all the available CEs have passive locomotion systems, and their reliance on peristalsis for passage through the intestine leads to significant limitations, in particular due to their unpredictable and variable locomotion velocities. For example, intermittent high transit speeds lead to incomplete visualisation of the intestinal surface, resulting in the potential for significant abnormalities to be missed. To improve the proportion of the lining that is visualised, patients must fast for 8–12 h before the procedure and for at least 4 h after ingestion of the capsule. In most cases, they are also required to drink 1–2 L of polyethylene glycol solution 12 h before the examination, in order to clear residual intestinal contents. Furthermore, the time taken for the capsule to pass varies from 14 to 70 h, with a transit time of 2–5 h through the oesophagus and stomach, 2–6 h for the small intestine, and 10–59 h for the large intestine [1]. Reviewing the images obtained during such lengthy transit periods means that the procedure of passive CE is considered both time-consuming and burdensome for clinicians. Considering all these drawbacks, an active locomotive mechanism for CE can dramatically reduce the procedure time and allow the endoscopist to focus the examination on areas of interest. In this study, we propose the model of an on-board vibro-impact self-propelled capsule system for examining the small intestine. The aim of this study is to understand the dynamics and efficient control of the system in the small intestinal environment, so that the results presented in this paper can be utilised for prototype design and fabrication.

To design a locomotive mechanism for such a small capsule is a challenging task due to its limited on-board space. Smart materials [2] and small-scale DC motors have been used to address this issue. For example, a CE with three active flexible legs controlled by means of an on-board microcontroller was constructed by using shape memory alloy [3]. The micro-actuation concept of the shape memory alloy was also used for the development of a 6-legged endoscopic capsule [4]. Legged CEs using on-board DC motors have been designed for 4 legs [5] and 12 legs [6, 7]. A small DC motor has been included in a small capsule to simultaneously control 8 polymer treads located on the outer surface [8]. In [9], a legged capsule controlled by an on-board DC motor and a slot-follower mechanism with a lead screw was developed. Lin and Yan [10] proposed an inch-like locomotion mechanism by using DC motor-driven legs and extension/retraction of the CE body. De Falco et al. [11] reported their work of a swimming wireless capsule that utilised four propellers independently activated by DC motors. In addition to such on-board locomotive mechanisms, external magnetic fields have also been adopted for capsule propulsion, see, e.g. [12,13,14]. Manipulation of the external magnet can alter the locomotive direction and orientation of the capsule. Such on-board and external driving mechanisms make it feasible to either move a capsule in a limited region or anchor it at a fixed location. However, the fabrication, manipulation, system reliability, and cost of such complex devices are the main barriers of development. Our work addresses these issues by employing the so-called vibro-impact self-propulsion approach [15,16,17]. Its advantages over the locomotion solutions described above include the fact that all the components can be located inside the capsule and no external accessories are required. This could potentially allow for simpler sterilisation of the capsule so that make it reusable. In addition, the cost of the components needed to produce this locomotion solution is small. Together, these attributes may significantly reduce the overall cost of CE, making it an attractive proposition to healthcare providers in both developed and developing countries.

The principle of vibro-impact self-propulsion is that bidirectional rectilinear motion of the capsule can be obtained by utilising internal vibration and impact force in the presence of external resistance. A prototype of the capsule robot propelled by internal interactive force and external friction was designed by Li et al. [18], and its velocity-dependent frictional resistance inside the intestine was experimentally investigated [19]. Carta et al. [20] developed a vibrational propelled capsule composed of a motor with an eccentric mass, which can produce a reduction in the friction with the environment. The motion of a complex micro-robot exhibiting impact and friction was studied numerically and experimentally using non-smooth multibody dynamics by Nagy et al. [21]. They found that the stiction and sliding of the robot were governed by the frequency of excitation and the friction, while impact around the resonant frequency of the oscillator does not contribute to the propulsion of the robot. Numerical simulations and experimental investigations of a vibration-driven capsule system under four different friction models were studied by Wang et al. [22]. This group have also considered the planar locomotion of a vibration-driven capsule with two internal masses [23]. In the current paper, we will discuss our vibro-impact capsule, which employs additional internal impact to enhance progression [16], and analyse its dynamic characteristics in a pig small intestine. Numerical studies [24, 25] suggest that forward and backward progression of the capsule can be controlled under either fast progression or energy-saving modes in different frictional environments. Preliminary experimental studies [26, 27] have demonstrated that the vibro-impact self-propulsion technique could be a potential alternative modality for active CE, and in particular, the provision of both forward and backward progression can improve both the quality and the sensitivity of clinical examinations. It is, therefore, useful to understand how the vibro-impact self-propelled capsule can be adapted to the intestinal environment in terms of selection of system and control parameters, such as mass ratio, stiffness ratio, and frequency and amplitude of excitation for prototyping and testing.

The remainder of this paper is organised as follows: In Sect. 2, the resistances exerted on the capsule by the intestinal tract are firstly studied and then employed in mathematical modelling of the vibro-impact capsule system. In Sect. 3, bifurcation analysis is performed to study the influences of various parameters on capsule dynamics and performance in terms of average velocity and energy efficiency. Finally, some concluding remarks are drawn in Sect. 4.

2 Mathematical modelling

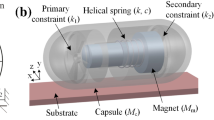
In this work, we consider the two-degrees-of-freedom dynamical capsule system as shown in Fig. 1a, where a movable internal mass \(m_1\) is driven by a harmonic excitation with forcing magnitude \(P_\mathrm{d}\) and frequency \(\Omega \). The internal mass interacts with a rigid capsule \(m_2\) via a linear spring with stiffness k and a viscous damper with damping coefficient c. The capsule has a cylindrical body with a hemispherical head and tail. Impact between the internal mass and a weightless plate connected to the capsule through a secondary spring with stiffness \(k_1\) may occur, once their relative displacement \(x_1-x_2\) is larger than or equal to the gap \(g_1\), where \(x_1\) and \(x_2\) are the absolute displacements of the internal mass and the capsule, respectively.

2.1 Resistances

As the diameter of the capsule is larger than the inner diameter of the small intestine, the capsule stretches the intestinal tract to yield hoop stress. This hoop stress causes normal and frictional forces on the capsule yielding environmental resistance which prevents the progression of the capsule. In addition, the gravity of the capsule which exerts normal pressure on the intestinal tract also adds additional value to the resistance. It is therefore that the overall resistance on the capsule can be written as

$$\begin{aligned} F_\mathrm{r}=F_\mathrm{hoop}+F_\mathrm{gravity}, \end{aligned}$$
(1)

where \(F_\mathrm{hoop}\) and \(F_\mathrm{gravity}\) represent the resistances introduced by hoop stress and capsule gravity, respectively. As depicted in Fig. 1b, the resistance due to hoop stress can be written as

$$\begin{aligned} F_\mathrm{hoop}=-{{\,\mathrm{sign}\,}}(v_2)(F_\mathrm{Hp}+F_\mathrm{Tp}+F_\mathrm{Hf}+F_\mathrm{Bf}+F_\mathrm{Tf}), \end{aligned}$$
(2)

where \(v_2\) is capsule speed, \(F_\mathrm{Hp}\) and \(F_\mathrm{Tp}\) are the normal pressures of the intestine on capsule head and tail, and \(F_\mathrm{Hf}\), \(F_\mathrm{Bf}\) and \(F_\mathrm{Tf}\) are the frictional forces exerted on the head, the body, and the tail, along the axial direction of the capsule, respectively. As the cross section of the small intestine is expanded by the capsule yielding tensile stress, hoop stress will depend on the geometric deformation of the intestinal wall. The geometric parameters of the capsule are shown in Fig. 1b, where L is the length of the capsule, \(R_\mathrm{c}\) is the radius of the head, the body, and the tail, \(R_\mathrm{i}\) is the original inner radius of the intestinal tract, \(\phi _\mathrm{c}\) is the angle of the point from where the intestinal tract starts to surround the capsule, and \(x_\mathrm{c}\) is the distance from the contact point to the centre of the head (or the tail).

Fig. 1
figure 1

(Colour online) a Physical model of the vibro-impact capsule in small intestine. b Resistances and geometric parameters of the capsule. The capsule is depicted in cyan with black shell, and the intestinal tract is displayed in light red

Full size image
Fig. 2
figure 2

(Colour online) a Hoop stress on the head and the body of the capsule. b Cross section of the intestinal tract. The intestinal tract without stretch is depicted in grey, and the tract with stretch is shown in light red

Full size image

As shown in Fig. 2a, a local frame \(\{x,\,o,\,R(x)\}\) is employed to calculate hoop stress in terms of variation of the inner intestinal radius, where \(x\in [0,\,2x_\mathrm{c}+L]\), \(x_\mathrm{c}=R_\mathrm{c}\cos \phi _\mathrm{c}\), and \(\cos \phi _\mathrm{c}=\sqrt{R_\mathrm{c}^2-R_\mathrm{i}^2}/R_\mathrm{c}\). When the capsule moves in a constant speed, according to this local frame, the intestine is stretched to yield the hoop strain given by

$$\begin{aligned} \epsilon (x)=\frac{R_\mathrm{i}-R(x)}{R_\mathrm{i}}, \end{aligned}$$
(3)

and therefore, the hoop stress which can be expressed using the five-element model [19, 28] as

$$\begin{aligned} \tau (x)=\epsilon (x)\left( E_1\text {e}^{-\frac{E_1 x}{\eta _1 v_2}}+E_2\text {e}^{-\frac{E_2 x}{\eta _2 v_2}}+E_3\right) , \end{aligned}$$
(4)

where \(E_1\), \(E_2\), and \(E_3\) represent the elastic property of the intestine, and \(\eta _1\) and \(\eta _2\) are viscosity coefficients. It is therefore that, as can be seen from Fig. 2b, the pressure between the capsule and the intestine due to hoop stress can be written as

$$\begin{aligned} q(x)=\frac{\tau (x)t_\mathrm{m}}{R(x)}, \end{aligned}$$
(5)

where \(t_\mathrm{m}\) is the mean thickness of the intestine. Consider that for every infinitesimal increment of x as shown in Fig. 2a, the corresponding normal pressure can be written as

$$\begin{aligned} \text {d}p(x)=q(x)\text {d}A(x)=q(x)2\pi R(x) \sqrt{1+R^{\prime }(x)^2}\text {d}x, \end{aligned}$$
(6)

where \(R^{\prime }(x)\) is the derivative of R(x) with respect to x [29]. Thus, the pressure on capsule head along the x-axis can be expressed as

$$\begin{aligned} F_\mathrm{Hp}=\int _{0}^{x_\mathrm{c}}\cos \phi (x)\text {d}p(x), \end{aligned}$$
(7)

where \(\cos \phi (x)=(x_\mathrm{c}-x)/R_\mathrm{c}\) for \(x\in [0,x_\mathrm{c}]\), and the friction force generated by normal pressure can be obtained using

$$\begin{aligned} F_\mathrm{Hf}=\int _{0}^{x_\mathrm{c}}\mu \sin \phi (x)\text {d}p(x), \end{aligned}$$
(8)

where \(\mu \) is the Coulomb friction coefficient. Similarly, the resistance on capsule tail can be obtained using

$$\begin{aligned} F_\mathrm{Tp}=\int _{x_\mathrm{c}+L}^{2x_\mathrm{c}+L}\cos \phi (x)\text {d}p(x), \end{aligned}$$
(9)

and

$$\begin{aligned} F_\mathrm{Tf}=\int _{x_\mathrm{c}+L}^{2x_\mathrm{c}+L}\mu \sin \phi (x)\text {d}p(x), \end{aligned}$$
(10)

where \(x\in [x_\mathrm{c}+L,2x_\mathrm{c}+L]\) and \(\cos \phi (x)=(x_\mathrm{c}+L-x)/R_\mathrm{c}<0\), which indicates a negative resistance due to the direction of the pressure on the tail. In addition, the frictional force on capsule body due to hoop stress can be written as

$$\begin{aligned} F_\mathrm{Bf}=\int _{x_\mathrm{c}}^{x_\mathrm{c}+L}\mu \text {d}p(x). \end{aligned}$$
(11)

Now, applying Eqs. (3–6) to (2), the resistance due to hoop stress can be written as

$$\begin{aligned}&F_\mathrm{hoop}=-{{\,\mathrm{sign}\,}}(v_2)\left( \int _{0}^{x_\mathrm{c}}\cos \phi (x)\text {d}p(x)\right. \nonumber \\&\qquad \left. +\,\int _{x_\mathrm{c}+L}^{2x_\mathrm{c}+L}\cos \phi (x)\text {d}p(x)\right. \nonumber \\&\qquad \left. +\,\int _{0}^{x_\mathrm{c}}\mu \sin \phi (x)\text {d}p(x)\right. \nonumber \\&\qquad \left. +\,\int _{x_\mathrm{c}}^{x_\mathrm{c}+L}\mu \text {d}p(x) +\int _{x_\mathrm{c}+L}^{2x_\mathrm{c}+L}\mu \sin \phi (x)\text {d}p(x)\right) \nonumber \\&\quad =-{{\,\mathrm{sign}\,}}(v_2)\left( 2\pi t_\mathrm{m} E_1\left( \frac{1}{R_\mathrm{i}} \left( \frac{\eta _1 |v_2|}{E_1}\right) ^2\right. \right. \nonumber \\&\qquad \left. \left. +\,\left( \mu -\frac{x_\mathrm{c}}{R_\mathrm{i}}\right) \left( \frac{\eta _1 |v_2|}{E_1}\right) -R_\mathrm{i}\right. \right. \nonumber \\&\qquad \left. \left. +\,\text {e}^{-\frac{E_1}{\eta _1 |v_2|}x_\mathrm{c}}\left( -\frac{1}{R_\mathrm{i}} \left( \frac{\eta _1 |v_2|}{E_1}\right) ^2-\mu \frac{R_\mathrm{c}}{R_\mathrm{i}} \left( \frac{\eta _1 |v_2|}{E_1}\right) \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. +\,R_\mathrm{c}+\left( \frac{E_1}{\eta _1 |v_2|}-\frac{\mu }{R_\mathrm{i}}\right) \int _{-x_\mathrm{c}}^{0}\text {e}^{-\frac{E_1 \xi }{\eta _1 |v_2|}} \sqrt{R_\mathrm{c}^2-\xi ^2}\text {d}\xi \right) \right. \right. \nonumber \\&\qquad \left. \left. +\,\text {e}^{-\frac{E_1}{\eta _1 |v_2|}(x_\mathrm{c}+L)}\left( \frac{1}{R_\mathrm{i}} \left( \frac{\eta _1 |v_2|}{E_1}\right) ^2+\mu \frac{R_\mathrm{c}}{R_\mathrm{i}} \left( \frac{\eta _1 |v_2|}{E_1}\right) \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. -\,R_\mathrm{c}+\left( \frac{E_1}{\eta _1 |v_2|}-\frac{\mu }{R_\mathrm{i}}\right) \int _{0}^{x_\mathrm{c}}\text {e}^{-\frac{E_1 \xi }{\eta _1 |v_2|}}\sqrt{R_\mathrm{c}^2-\xi ^2}\text {d}\xi \right) \right. \right. \nonumber \\&\qquad \left. \left. +\,\text {e}^{-\frac{E_1}{\eta _1 |v_2|}(2x_\mathrm{c}+L)} \left( -\frac{1}{R_\mathrm{i}}\left( \frac{\eta _1 |v_2|}{E_1}\right) ^2\right. \right. \right. \nonumber \\&\qquad \left. \left. \left. -\,\left( \mu +\frac{x_\mathrm{c}}{R_\mathrm{i}}\right) \left( \frac{\eta _1 |v_2|}{E_1}\right) +R_\mathrm{i}\right) \right) \right. \nonumber \\&\qquad \left. +\,2\pi t_\mathrm{m} E_2\left( \frac{1}{R_\mathrm{i}} \left( \frac{\eta _2 |v_2|}{E_2}\right) ^2\right. \right. \nonumber \\&\qquad \left. \left. +\,\left( \mu -\frac{x_\mathrm{c}}{R_\mathrm{i}}\right) \left( \frac{\eta _2 |v_2|}{E_2}\right) -R_\mathrm{i}\right. \right. \nonumber \\&\qquad \left. \left. +\,\text {e}^{-\frac{E_2}{\eta _2 |v_2|}x_\mathrm{c}}\left( -\frac{1}{R_\mathrm{i}} \left( \frac{\eta _2 |v_2|}{E_2}\right) ^2-\mu \frac{R_\mathrm{c}}{R_\mathrm{i}} \left( \frac{\eta _2 |v_2|}{E_2}\right) \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. +\,R_\mathrm{c}+\left( \frac{E_2}{\eta _2 |v_2|}-\frac{\mu }{R_\mathrm{i}}\right) \int _{-x_\mathrm{c}}^{0}\text {e}^{-\frac{E_2 \xi }{\eta _2 |v_2|}}\sqrt{R_\mathrm{c}^2-\xi ^2}\text {d}\xi \right) \right. \right. \nonumber \\&\qquad \left. \left. +\,\text {e}^{-\frac{E_2}{\eta _2 |v_2|}(x_\mathrm{c}+L)}\left( \frac{1}{R_\mathrm{i}} \left( \frac{\eta _2 |v_2|}{E_2}\right) ^2\right. \right. \right. \nonumber \\&\qquad \left. \left. \left. +\,\mu \frac{R_\mathrm{c}}{R_\mathrm{i}} \left( \frac{\eta _2 |v_2|}{E_2}\right) -R_\mathrm{c} +\left( \frac{E_2}{\eta _2 |v_2|}-\frac{\mu }{R_\mathrm{i}}\right) \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. \times \,\int _{0}^{x_\mathrm{c}}\text {e}^{-\frac{E_2 \xi }{\eta _2 |v_2|}}\sqrt{R_\mathrm{c}^2-\xi ^2}\text {d}\xi \right) \right. \right. \nonumber \\&\qquad \left. \left. +\,\text {e}^{-\frac{E_2}{\eta _2 |v_2|}(2x_\mathrm{c}+L)}\left( -\frac{1}{R_\mathrm{i}}\left( \frac{\eta _2 |v_2|}{E_2}\right) ^2\right. \right. \right. \nonumber \\&\qquad \left. \left. \left. -\,\left( \mu +\frac{x_\mathrm{c}}{R_\mathrm{i}}\right) \left( \frac{\eta _2 |v_2|}{E_2}\right) +R_\mathrm{i}\right) \right) \right. \nonumber \\&\qquad \left. +\,2\pi t_\mathrm{m} E_3\mu \left( x_\mathrm{c}-\frac{R_\mathrm{c}^2}{R_\mathrm{i}}\tan ^{-1} \left( \frac{x_\mathrm{c}}{R_\mathrm{i}}\right) -L\frac{R_\mathrm{c}-R_\mathrm{i}}{R_{\mathrm{i}}}\right) \right) . \end{aligned}$$
(12)

The frictional resistance caused by the gravity of the capsule can be given as

$$\begin{aligned} F_\mathrm{gravity}=-{{\,\mathrm{sign}\,}}(v_2)\left( m_1+m_2\right) g\mu \cos \gamma , \end{aligned}$$
(13)

where g and \(\gamma \) are the acceleration due to gravity and the inclination of the intestine, respectively.

Table 1 Physical parameters of the pig small intestine
Full size table
Fig. 3
figure 3

Resistances introduced by a the hoop stress \(F_\mathrm{hoop}\) and b capsule’s gravity \(F_\mathrm{gravity}\) as a function of the capsule velocity \(v_2\) calculated for \(R_\mathrm{c}=4\) (mm), \(L=10\) (mm), \(g=9.81\) (m/s\(^{2}\)) and \(m_1+m_2=0.04\) (kg). Variations of the hoop resistance \(F_\mathrm{hoop}\) under varying c radius \(R_\mathrm{c}\) and d length L

Full size image

Physical parameters of the pig small intestinal tract used in the following simulations are listed in Table 1. Based on these parameters, calculations of the resistances due to hoop stress and the gravity of the capsule with respect to capsule velocity are presented in Fig. 3, where \(F_\mathrm{hoop}\) in Fig. 3a is a typical Stribeck friction and \(F_\mathrm{gravity}\) in Fig. 3b is a classical Coulomb friction. Figure 3c, d illustrates variations of the resistance caused by the hoop stress \(F_\mathrm{hoop}\) in terms of capsule’s radius \(R_\mathrm{c}\) and length L, respectively. From these two figures, one can observe that both the threshold and the maximal value of the resistance will increase if either \(R_\mathrm{c}\) or L increases, and the resistance \(F_\mathrm{hoop}\) is more sensitive to capsule’s radius \(R_\mathrm{c}\).

2.2 Equations of motion

As depicted in Fig. 1, a periodic external force, \(P_\mathrm{d}\cos (\Omega t)\), is applied on the inner mass \(m_1\) to drive the capsule \(m_2\). The inner mass interacts with the capsule via a damped spring at the tail and a secondary spring at the head of the capsule. Due to the gap between the mass and the secondary spring, \(g_1\), the interaction between \(m_1\) and \(m_2\) keeps switching between two phases: no contact (\(x_1-g_1-x_2<0\)) and contact (\(x_2-g_1-x_1\ge 0\)). Therefore, the mutual interactive force between the inner mass and the capsule can be calculated as

$$\begin{aligned} F_i={\left\{ \begin{array}{ll} -c(\dot{x}_1-\dot{x}_2)-k(x_1-x_2),&{}\quad \text {for}\quad x_1-g_1-x_2<0\\ -c(\dot{x}_1-\dot{x}_2)-k(x_1-x_2)-k_1(x_1-g_1-x_2),&{}\quad \text {for}\quad x_2-g_1-x_1\ge 0 \end{array}\right. } \end{aligned}$$
(14)

or

$$\begin{aligned} F_i=-c(\dot{x}_1-\dot{x}_2)-k(x_1-x_2)-H_{1}k_1(x_1-g_1-x_2), \end{aligned}$$
(15)

where \(H_1\) is the Heaviside function given by

$$\begin{aligned} {\begin{matrix} H_1=&H(x_1-g_1-x_2). \end{matrix}} \end{aligned}$$
(16)

Here, a detailed consideration of these switching phases can be found from [16, 24]. Finally, the comprehensive equations of motion for the vibro-impact capsule system are written as

$$\begin{aligned} \begin{aligned} \dot{x}_1&=v_1,\\ \dot{v}_1&=\tfrac{1}{m_1}[P_\mathrm{d}\cos (\Omega t)+F_i]-g \sin \gamma ,\\ \dot{x}_2&=v_2,\\ \dot{v}_2&=-\tfrac{1}{m_2}[F_i-F_\mathrm{hoop}-F_\mathrm{gravity}]-g \sin \gamma . \end{aligned} \end{aligned}$$
(17)

3 Bifurcation analysis

As described by Eq. (17), a periodic driving force is implemented to overcome the environmental resistance for capsule progression. Intuitive speaking, a large driving force and a small resistance are preferred for fast capsule progression. As can be seen from Fig. 3, resistance becomes larger once the radius or the length of the capsule increases. Therefore, our bifurcation analysis in this paper will focus on the driving force and the dimension of the capsule system. For bifurcation diagrams, we have adopted the velocity \(v^*_1\)–\(v^*_2\), which is a projection of the Poincaré map on the \(v_1\)–\(v_2\) axis, as a function of the magnitude/frequency of the driving force. Calculations were performed for 300 cycles of the driving force, and the data for the first 280 cycles were omitted to ensure steady-state responses, whereas the next 20 values of the relative velocity, \(v^*_1\)–\(v^*_2\), were plotted in bifurcation diagrams.

In order to study the capsule’s performance in the small intestine, the average speed of progression given by

$$\begin{aligned} v_\mathrm{avg}=\frac{x_2(N T)-x_2(0)}{N t} \end{aligned}$$
(18)

and the energy efficiency expressed as

$$\begin{aligned} x_E=\frac{x_2(N T)-x_2(0)}{\int _{0}^{N T}P_\mathrm{d}\cos (\Omega t)\text {d}t} \end{aligned}$$
(19)

were calculated, where N and \(T=\frac{2\pi }{\Omega }\) are the number of cycles and the period of driving force, respectively. For simplicity, the abbreviation P-m-n is used to denote the period-m motion with n impacts per period of the driving force.

3.1 Influence of intestinal resistances

Our first numerical study has focused on the dynamics of the capsule under various magnitudes of the driving force, \(P_\mathrm{d}\), as shown in Fig. 4. As can be seen from Fig. 4a, most of the capsule responses are P-1-1, except the P-2-2 motion for \(P_\mathrm{d}\in [2.7,6.7]\) (mN). In Fig. 4b, our calculations show that the average progression speed of the capsule increases with the increase in magnitude of the driving force until \(P_\mathrm{d}\ge 14.4\) (mN) from where the capsule gradually slows down its forward motion. When \(P_\mathrm{d}\le 0.4\) (mN), the driving force is too small such that the capsule cannot overcome its intestinal resistances. Thereafter, as shown in Fig. 4c, the energy efficiency, \(x_E\), experiences a rapid growth until \(P_\mathrm{d}=2.7\) (mN) when a period doubling of the capsule is encountered. It is obvious that the P-2-2 motion weakens capsule’s performance in terms of energy consumption. As the magnitude of the driving force increases further, a reverse period doubling is observed at \(P_\mathrm{d}=6.6\) (mN) followed by a P-1-1 response of the capsule with decreased energy efficiency.

Fig. 4
figure 4

(Colour online) a Bifurcation diagram, b average velocity, and c energy efficiency constructed for varying the magnitude of the driving force, \(P_\mathrm{d}\) calculated for \(R_\mathrm{c}=3.91\) (mm), \(L=10\) (mm), \(m_1=0.001\) (kg), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(g_1=1\) (mm), \(\Omega =31\) (rad/s), and \(\gamma =0\) (rad). d–f The trajectories of the capsule system on the phase plane (\(x_1\)–\(x_2\), \(v_1\)–\(v_2\)), and g–i the time histories of the inner mass (black lines) and the capsule (red lines) for \(P_\mathrm{d}=2.6\) (mN), 5 (mN), and 8 (mN), respectively. The locations of the impact surface are shown by vertical black lines, and Poincaré sections are marked by blue dots

Full size image
Fig. 5
figure 5

(Colour online) a Bifurcation diagram, b average velocity, and c energy efficiency constructed for varying the magnitude of the driving force, \(P_\mathrm{d}\) calculated for \(R_\mathrm{c}=4\) (mm), \(L=10\) (mm), \(m_1=0.001\) (kg), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(g_1=1\) (mm), \(\Omega =31\) (rad/s), and \(\gamma =0\) (rad). Coexisting attractors are marked by circles. d–j The trajectories of the capsule system on the phase plane (\(x_1\)–\(x_2\), \(v_1\)–\(v_2\)), and k–q the time histories of the inner mass (black lines) and the capsule (red lines) for \(P_\mathrm{d}=5\) (mN), 6.9 (mN), 8 (mN), 9 (mN), 10 (mN), 13 (mN) and 15 (mN), respectively. The locations of the impact surface are shown by vertical black lines, and Poincaré sections are marked by red dots

Full size image

When the radius of the capsule increases slightly from \(R_\mathrm{c}=3.91\) (mm) to 4 (mm), the bifurcation pattern presented in Fig. 5a becomes more complex. After the first period doubling recorded at \(P_\mathrm{d}=6.6\) (mN), a grazing bifurcation occurs to yield the coexistence of P-2-2 and P-2-3 motions for \(P_\mathrm{d}\in [6.8,9]\). The P-2-2 motion disappears next, leaving only the P-2-3 motion which then bifurcates into a P-4-6 motion through the second period doubling at \(P_\mathrm{d}=8.5\) (mN) as shown in Fig. 5g, n. As the magnitude of the driving force \(P_\mathrm{d}\) increases, the motion of the capsule becomes chaotic as shown in Fig. 5h, o. Thereafter, two successive bifurcations of reverse period doubling are observed at \(P_\mathrm{d}=12.4\) and 14.6 (mN), which yield a P-4-6 and P-2-3 motions as demonstrated in Fig. 5i, j, respectively. Comparing the average velocity shown in Fig. 5b, as the threshold of the resistances elevated by the increase in capsule’s radius, \(R_\mathrm{c}\), the starting point of capsule progression is postponed from \(P_\mathrm{d}=0.5\) (mN) to 1.2 (mN), which means that a larger driving force is required to overcome the external resistance. With respect to the increase of \(P_\mathrm{d}\), the average capsule velocity, \(v_\mathrm{avg}\), keeps growing, with a sudden jump induced by the grazing bifurcation at \(P_\mathrm{d}=7\) (mN). It is remarkably shown in Fig. 5b that a larger resistance (i.e. a larger radius of the capsule) does not always result in a slower capsule progression. When \(P_\mathrm{d}\) keeps increasing beyond 14.2 (mN), the average velocity of the capsule for \(R_\mathrm{c}=4\) (mm) is faster than the one for \(R_\mathrm{c}=3.91\) (mm). However, as shown in Fig. 5c, the capsule with a smaller radius presents much higher energy efficiency.

Fig. 6
figure 6

(Colour online) Bifurcation diagrams for a\(R_\mathrm{c}=4.2\) (mm) and b 4.4 (mm), c average velocity, and d energy efficiency constructed for varying the magnitude of the driving force, \(P_\mathrm{d}\), where the rest of the parameters were chosen as \(L=10\) (mm), \(m_1=0.001\) (kg), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(g_1=1\) (mm), \(\Omega =31\) (rad/s), \(\gamma =0\) (rad). Coexisting attractors are marked by circles. e–g Evolution of basins of attraction for the blue netted area of b

Full size image

As the radius of the capsule, \(R_\mathrm{c}\), increases further, as shown in Fig. 6, the responses of the capsule become simpler compared to the responses obtained for \(R_\mathrm{c}=4\) (mm). As can be seen from Fig. 6a, b, both cases are dominated by period-two motion and the time of impact per period of excitation switches from three to two via grazing bifurcation. To illustrate the coexistence of two different attractors observed in Fig. 6, the region for \(P_\mathrm{d}\in [6.8,9]\) in Fig. 6b was marked by netted blue to indicate the coexisting P-2-3 and P-2-2 motions. Their corresponding basins of attraction at \(P_\mathrm{d}=7\) (mN), 8 (mN), and 9 (mN) are presented in Fig. 6e–g, respectively, where the initial displacement and velocity of the capsule were fixed as zero, with only the initial conditions of \(x_1\) and \(v_1\) varying. As can be seen from the basins, there are two white regions for the initial conditions leading to P-2-3 motion with all the other purple region resulting in P-2-2 motion. As the forcing magnitude increases, the basin of P-2-3 shrinks slightly.

It also can be observed from Fig. 6c that the contribution of P-1-1 to capsule progression for both \(R_\mathrm{c}=4.2\) (mm) and 4.4 (mm) is nearly invisible as their resulting driving forces are insufficient to make considerable progression for the entire capsule system. In general, the enlargement of \(R_\mathrm{c}\) increases the resistances in the intestinal tract and the energy dissipation of the capsule, so degrades its energy efficiency. However, Fig. 6c shows that the capsule with a larger radius might result in a faster average velocity when the driving force is sufficiently large. In addition, \(x_E\) for \(R_\mathrm{c}=4.4\) (mm) in Fig. 6d is negative for \(P_\mathrm{d}\in [4.9,5.7]\) (mN), which demonstrates a slow backward motion of the capsule.

Fig. 7
figure 7

(Colour online) a Average velocity and b energy efficiency as functions of \(P_\mathrm{d}\) calculated for \(R_\mathrm{c}=4.3\), \(m_1=0.001\) (kg), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(g_1=1\) (mm), \(\Omega =31\) (rad/s), and \(\gamma =0\) (rad)

Full size image

As can be seen from Fig. 2, the capsule length, L, has a significant influence on the resistance in the intestinal tract. Intuitively, the longer of the capsule, the larger resistance in the tract, so that the slower of capsule progression. Figure 7 presents the average speeds and the energy efficiencies of the capsule for various lengths of the capsule, and different periodic responses of the capsule are marked in the figure. As can be seen from Fig. 7a, period doubling is critical for capsule progression, since the period-one motions produced by small driving force cannot overcome the resistances in the tract, but visible progression can be observed after the period-doubling bifurcation from P-1-1 to P-2-2. As \(P_\mathrm{d}\) increases, the P-2-2 motion on each curve successively bifurcates into P-2-3 via grazing bifurcation, except for the red curve for \(L=11\) (mm). In addition, the green and purple curves for long capsules (\(L=14\) (mm) and 17 (mm)) undergo another grazing bifurcation when the driving force is sufficiently large, which switches P-2-3 into P-2-2 again. Comparing both \(v_\mathrm{avg}\) and \(x_E\), our calculations prove that a shorter capsule has faster average speed and better efficiency for energy consumption.

Fig. 8
figure 8

(Colour online) a Bifurcation diagram and b average velocity constructed for varying the frequency of the driving force, \(\Omega \), calculated for \(R_\mathrm{c}=4\) (mm), \(L=10\) (mm), \(m_1=0.001\) (kg), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(g_1=1\) (mm), \(\gamma =0\) (rad), and \(P_\mathrm{d}=8\) (mN). Coexisting attractors are denoted by circles. c–i The trajectories of the capsule system on the phase plane (\(x_1\)–\(x_2\), \(v_1\)–\(v_2\)), and j–p present the time histories of the inner mass (black lines) and the capsule (red lines) for \(\Omega =13\) (rad/s), 15 (rad/s), 20 (rad/s), 28 (rad/s), 32 (rad/s), 32.4 (rad/s), and 34 (rad/s). The locations of the impact surface are shown by vertical solid lines, and Poincaré sections are marked by blue dots

Full size image
Fig. 9
figure 9

(Colour online) Bifurcation diagrams for a\(P_\mathrm{d}=12\) (mN), b\(P_\mathrm{d}=16\) (mN), c average velocity, and d energy efficiency as functions of the driving frequency, \(\Omega \), calculated for \(R_\mathrm{c}=4\), \(L=10\) (mm), \(m_1=0.001\) (kg), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(g_1=1\) (mm) and \(\gamma =0\) (rad). Coexisting attractors are denoted by circles

Full size image

To sum up, it can conclude that increasing the driving force will benefit the average velocity of the capsule but can decrease its corresponding energy efficiency. It has also shown that increasing the capsule’s size will enlarge the resistances on the capsule introducing more period-two responses for the system. The occurrence of period-two motion always slows down the capsule and decreases its energy efficiency. However, this does not mean that the capsule’s size needs to be as small as possible, because larger resistances can restrain capsule’s backward motion and produce faster progression when the driving force is sufficiently large.

3.2 Influence of the magnitude and frequency of the driving force

Figure 8 shows bifurcation diagram and average velocity of the capsule as functions of the driving frequency, \(\Omega \). In order to use resonance to enhance capsule progression, the branching parameter, \(\Omega \), was varied around the natural frequency of the inner mass, i.e.

$$\begin{aligned} \omega _\mathrm{n}=\sqrt{\frac{k}{m_1}}=31.62 \text { (rad/s)}. \end{aligned}$$

When driving frequency is relatively low (\(\Omega <30\) (rad/s)), it can be seen from Fig. 8a that the capsule undergoes a series of successive grazing bifurcations as \(\Omega \) increases. Panels (c–f) demonstrate these bifurcations showing the variation of capsule dynamics from P-1-4 to P-1-1. These successive grazing bifurcations induce a number of “jumps” on the average speed of the capsule as presented in Fig. 8b, which remarkably shows that \(v_\mathrm{avg}\) reaches its local maximum after each “jump”. As \(\Omega \) increases (\(\Omega >30\) (rad/s)), a period doubling which leads to a P-2-3 motion and a sudden drop on \(v_\mathrm{avg}\) can be observed at \(\Omega =30.4\) (rad/s). Thereafter, two coexisting P-2-3 and P-2-2 motions were recorded for \(\Omega =32.2\) (rad/s). The P-2-2 motion bifurcates again into a P-1-1 motion at \(\Omega =33\) (rad/s) through a reverse period doubling, and the average speed of capsule progression, \(v_\mathrm{avg}\), keeps increasing as the forcing frequency increases.

As shown in Fig. 9, once the driving force is gradually increased, the dynamics of the capsule becomes more complex, with several regions having multistable dynamics. When \(P_\mathrm{d}\) is 12 (mN), the bifurcation pattern of the system is almost the same as the one for \(P_\mathrm{d}=8\) (mN), except the cascade period doubling on the period-2 branch, which induces a small parametric window of chaos. Further increasing \(P_\mathrm{d}\) to 16 (mN) makes bifurcation pattern more complex as stronger excitation incurs larger-amplitude vibration involving two nonlinearities, impact and friction. As a result, Fig. 9b displays more period-doubling bifurcations for relatively low \(\Omega \) (\(\Omega <30\) (rad/s)). When \(\Omega \) is relatively high (\(\Omega >30\) (rad/s)), the parametric regime for P-1-1 can be shrunk as the driving force increases.

Fig. 10
figure 10

(Colour online) Bifurcation diagrams for a\(k=0.5\) (N/m), b\(k=0.7\) (N/m), c\(k=0.9\) (N/m), d average velocity, and e energy efficiency as functions of the driving frequency, \(\Omega -\omega _\mathrm{n}\), calculated for \(R_\mathrm{c}=4\) (mm), \(L=10\) (mm), \(m_1=0.002\) (kg), \(m_2=0.003\) (kg), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(g_1=1\) (mm), \(\gamma =0\) (rad), and \(P_\mathrm{d}=12\) (mN)

Full size image
Fig. 11
figure 11

(Colour online) Bifurcation diagrams for a\(m_1=0.001\) (kg), b\(m_2=0.002\) (kg), c\(m_3=0.003\) (kg), d average velocity, and e energy efficiency as functions of the driving frequency, \(\Omega -\omega _\mathrm{n}\), calculated for \(R_\mathrm{c}=4\) (mm), \(L=10\) (mm), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(g_1=1\) (mm), \(\gamma =0\) (rad) and \(P_\mathrm{d}=12\) (mN)

Full size image

It can be seen from Fig. 9c that, when \(P_\mathrm{d}=16\) (mN), the average progression of the capsule is remarkably reduced once period-2 motion occurs. Comparing the average velocities for different magnitudes of the driving force when \(\Omega >40\) (rad/s), it shows that high frequency and large magnitude of the driving force cannot improve capsule progression, and this in turn degrades the energy efficiency of the capsule as shown in Fig. 9d. According to Fig. 9c, d, it can be concluded that the best regime for the frequency of the driving force is the P-1-2 motion around \(\Omega =20\) (rad/s), where a compromise between average speed and energy efficiency can be made.

Fig. 12
figure 12

(Colour online) Bifurcation diagrams for a\(k_1=4\) (N/m), b\(k_1=8\) (N/m), c\(k_1=12\) (N/m), d average velocity, and e energy efficiency as functions of the driving frequency, \(\Omega \), calculated for \(R_\mathrm{c}=4\) (mm), \(L=10\) (mm), \(m_1=0.002\) (kg), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(c=0.001\) (Ns/m), \(g_1=1\) (mm), \(\gamma =0\) (rad), and \(P_\mathrm{d}=12\) (mN)

Full size image
Fig. 13
figure 13

(Colour online) a Bifurcation diagram, b average velocity, and c energy efficiency as functions of the forcing frequency, \(\Omega \), calculated for \(R_\mathrm{c}=4\) (mm), \(L=10\) (mm), \(m_1=0.002\) (kg), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(P_\mathrm{d}=12\) (mN), \(\gamma =0\) (rad), and \(g_1=-3\) (mm). d–l and m–u illustrate phase trajectories and time histories for \(\Omega =12.86\) (rad/s), 12.96 (rad/s), 17.56 (rad/s), 22.96 (rad/s), 24.66 (rad/s), 25.66 (rad/s), 25.76 (rad/s), 27.46 (rad/s), and 29.06 (rad/s), respectively

Full size image

3.3 Influence of the natural frequency of the inner mass

If the stiffness of the primary spring or the weight of the inner mass varies, the natural frequency of the inner mass, \(\omega _\mathrm{n}\), will be changed. Then, the driving frequency, \(\Omega \), should be adjusted accordingly to match such variations. In this subsection, we will study the influence of the natural frequency of the inner mass on capsule dynamics by varying the stiffness of the primary spring and the weight of the inner mass. Firstly, bifurcation diagrams for \(k=0.5\) (N/m), 0.7 (N/m), and 0.9 (N/m) under variation of the driving frequency, \(\Omega \), are shown in Fig. 10a–c, respectively. As can be seen from these figures, the range for the driving frequency was chosen in the vicinity of its corresponding natural frequency, \(\Omega \in [\omega _\mathrm{n}-10,\omega _\mathrm{n}+10]\). In general, these bifurcations are very similar, and the only difference is that the larger the stiffness of the primary spring, the less the number of the period doubling. In addition, for the same type of capsule dynamics, say P-1-2 motions in Fig. 10a–c, the capsule with a smaller k has larger average velocity. Regardless of the stiffness of the primary spring, the fastest progression was achieved just after the occurrence of the grazing bifurcation when the capsule bifurcates from P-1-3 to P-1-2 motion. Figure 10d shows that the efficiencies of the capsule for different stiffness are very close, so changing the stiffness of the primary spring does not affect the efficiency of the system.

Fig. 14
figure 14

(Colour online) Bifurcation diagrams for a\(g_1=-1\) (mm), b\(g_1=1\) (mm), c\(g_1=3\) (mm), d average velocity, and e energy efficiency as functions of the forcing frequency, \(\Omega \), calculated for \(R_\mathrm{c}=4\) (mm), \(L=10\) (mm), \(m_1=0.002\) (kg), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(P_\mathrm{d}=12\) (mN), and \(\gamma =0\) (rad). Coexisting attractors are denoted by circles

Full size image

Apart from the stiffness of the primary spring, the weight of the inner mass, \(m_1\), also affects the natural frequency of the inner mass. When \(m_1\) is increased from 0.001 (kg) to 0.003 (kg), as shown in Fig. 11, the number of period-doubling bifurcations reduces. Since period-two motion retards capsule velocity, it can be observed from Fig. 11d that the capsule has a faster average velocity when its inner mass is heavier. However, the efficiency of the capsule is not affected by \(m_1\) as their local maxima are very close as shown in Fig. 11e.

In summary, both grazing bifurcation for \(\Omega <\omega _\mathrm{n}\) and period doubling for \(\Omega \) near \(\omega _\mathrm{n}\) were observed. When \(\Omega \) is much larger than \(\omega _\mathrm{n}\), the capsule has P-1-1 motion, and increasing \(\Omega \) will degrade the energy efficiency of the system. When the magnitude of the driving force is increased, the average speed of the capsule is sensitive to the frequency of the driving force, and its energy efficiency will decrease. If the stiffness of the primary spring is reduced or the weight of the inner mass is increased, i.e. decreasing the natural frequency of the inner mass, the average speed of the capsule can be enhanced while maintaining the energy efficiency unchanged.

Fig. 15
figure 15

a Average velocity as a function of the forcing magnitude, \(P_\mathrm{d}\), calculated for \(R_\mathrm{c}=4\) (mm), \(L=10\) (mm), \(m_1=0.001\) (kg), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(g_1=1\) (mm), and \(\Omega =22\) (rad/s). Extra windows demonstrate phase trajectories and time histories of the capsule for \(P_\mathrm{d}=10\) (mN), b, f\(\gamma =0.05\) (rad), c, g 0.15 (rad), d, h 0.25 (rad), and e, i 0.35 (rad)

Full size image
Fig. 16
figure 16

a Average velocity as a function of the forcing magnitude, \(P_\mathrm{d}\), calculated for \(L=10\) (mm), \(m_1=0.001\) (kg), \(m_2=0.003\) (kg), \(k=1\) (N/m), \(k_1=9\) (N/m), \(c=0.001\) (Ns/m), \(g_1=1\) (mm), \(\Omega =22\) (rad/s), and \(\gamma =0.2\) (rad). Extra windows demonstrate phase trajectories and time histories of the capsule for \(P_\mathrm{d}=30\) (mN), b, g\(R_\mathrm{c}=4.1\) (mm), c, h 4.2 (mm), d, i 4.3 (mm), e, j 4.4 (rad), and f, k 4.5 (mm)

Full size image

3.4 Influence of the stiffness of the secondary spring

The stiffness of the secondary spring is another control parameter affecting the performance of the capsule. As shown in Fig. 12, hardening the secondary spring enlarges the parametric region of period-two motion degrading the average speed of the capsule. For \(k_1=4\) (N/m), there is only a small region for P-2-2 motion. When \(k_1\) was increased to 8 (N/m), the region was expanded and a grazing bifurcation for the switching from P-2-3 to P-2-2 was recorded. When \(k_1=12\) (N/m), an additional period doubling from P-2-2 to P-4-6 was observed. Comparing the average velocity of the capsule, as can be seen from Fig. 12d, the capsule with a stiffer secondary spring has faster average speed when the driving frequency is low (i.e. before the grazing bifurcation from P-1-2 to P-1-1), but slower average speed for high driving frequency (i.e. after the grazing bifurcation). Similar trend can be observed from the energy efficiency presented in Fig. 12e. It can be seen that, after the grazing bifurcation from P-1-2 to P-1-1, the energy efficiencies of the capsules with different secondary springs are similar, but the period-doubling bifurcation degrades the performance of the capsule. After the reverse period doubling, i.e. when the dynamics of the capsule bifurcates into P-1-1 motion, the capsule with a stiffer secondary spring has better energy efficiency.

3.5 Influence of the contact gap

The influence of the contact gap between the inner mass and the secondary spring is considered in this subsection. Firstly, a negative gap, \(g_1=-3\) (mm), representing a prestressed secondary spring, is studied, and its bifurcation diagram as a function of the forcing frequency, \(\Omega \), is presented in Fig. 13. The bifurcation diagram shown in Fig. 13a has similar bifurcation pattern as the previous ones (i.e. a grazing bifurcation followed by a period doubling), but around \(\Omega =25\) (rad/s), which is slightly higher than the natural frequency of the inner mass, the capsule has chaotic and period-3 motions.

When the driving frequency is low, \(\Omega <12.96\) (rad/s), the capsule experiences P-1-4 motion as demonstrated in Fig. 13d, m, and bifurcates into P-1-3 via a grazing bifurcation. The capsule bifurcates from P-1-3 to P-1-2 via the second grazing bifurcation recorded at \(\Omega =16.66\) (rad/s) with the coexistence of P-1-3 and P-1-2 motions recorded for \(\Omega \in [16.26, 16.66]\) (rad/s) and then from P-1-2 to P-2-4 through a period doubling at \(\Omega =16.86\) (rad/s). For \(\Omega =18.26\) (rad/s), a reverse period doubling occurs and the capsule experiences P-1-2 again until \(\Omega =23.86\) (rad/s), where a cascade of period-doubling bifurcations leads the capsule to a chaotic motion for \(\Omega \in [24.26,25.96]\) (rad/s) including a small window of P-3-5 motion for \(\Omega \in [24.46,25.06]\) (rad/s). As the frequency increases, a cascade of reverse period-doubling bifurcations was recorded, and the capsule eventually settles down at a P-1-1 motion.

The maximum average speed of the capsule can be obtained at where the grazing bifurcation from P-1-3 to P-1-2 occurs as shown in Fig. 13b. As the frequency increases, the average speed of the capsule decreases. When the frequency was increased to \(\Omega =\omega _\mathrm{n}=22.36\) (rad/s), capsule speed was enhanced again by the resonance. As can be observed from Fig. 13c, the P-1-1 motion after the reverse period doubling has the best efficiency in energy consumption. However, the energy efficiency of the P-1-2 motion (for the maximum average speed) is not far from the best efficiency obtained by the P-1-1 motion, so the P-1-2 motion is a better choice in terms of both performance indices.

Bifurcation diagrams for different gaps under variation of the forcing frequency are shown in Fig. 14. As the gap increases, bifurcations of the capsule become simpler. For example, as can be seen from Fig. 14a, the regions for chaotic motion and coexisting P-1-3 and P-1-2 motions were significantly shrunk compared to the one for \(g_1=-3\) (mm). When the gap becomes positive as shown in Fig. 14b, c, chaotic motions are completely removed and only period-two motions exist. Comparing the average velocity of the capsule shown in Fig. 14d, it can be seen that local maxima of the average velocities for different gaps can be obtained after each grazing bifurcation, and the capsule with \(g_1=3\) (mm) has the maximal average velocity after its grazing bifurcation from P-1-2 to P-1-1. Energy efficiencies presented in Fig. 14e demonstrate that the capsules with different gaps have similar efficiencies for energy consumption after their grazing bifurcations from P-1-2 to P-1-1.

3.6 Progression in an inclined intestine

Our previous studies have focused on the capsule progression along a horizontal small intestinal tract. In the real environment, as the gastrointestinal tract is folded inside human body, it may require the capsule to progress along an inclined intestine, i.e. \(\gamma >0\). Influence of the inclined slope on capsule progression is studied here by calculating the average velocity of the capsule as a function of the forcing magnitude as presented in Fig. 15. It can be seen that the capsule has zero average velocity for all the inclined slopes when driving force is small. As the magnitude of the driving force increases, forward progression of the capsule can be observed, where the capsule moves faster for smaller angle of the slope. It is worth noting that a larger driving force does not always lead to a faster progression, especially when the angle of the slope is large, e.g. \(\gamma =0.25\) (rad) and 0.35 (rad), which yields backward progression (negative average velocity of the capsule) as the driving force increases.

To progress forward along an inclined intestine, the capsule needs to overcome its own gravity, and the only external resource it can utilise is the environmental resistance. According to Fig. 3c, the capsule with a larger radius is required to generate larger resistance so that the capsule can progress forward along a steeper slope. This study is shown in Fig. 16, where the average velocity of the capsule was calculated as a function of the forcing magnitude under variations of capsule’s radius. As can be seen from Fig. 16a, when the forcing magnitude increases, the average speed of the capsule starts to successively increase from zero to a positive value. However, the capsule with \(R_\mathrm{c}=4.1\) (mm) firstly slows down its forward progression and begins to move backward when \(P_\mathrm{d}=28.4\) (mN). When \(R_\mathrm{c}\) is 4.2 (mm), the capsule moves slower than that for \(R_\mathrm{c}=4.1\) (mm) when \(P_\mathrm{d}<13.9\) (mN), but has a better progression when \(P_\mathrm{d}\ge 13.9\) (mN). Similar phenomenon can be observed when \(R_\mathrm{c}\) is increased to 4.3 (mm), which yields a faster progression than that for \(R_\mathrm{c}=4.2\) (mm) once \(P_\mathrm{d}\ge 29.2\) (mN). Based on our calculations, the capsule with \(R_\mathrm{c}=4.2\) (mm) and the forcing magnitude, \(P_\mathrm{d}\in [13.9, 29.2)\) (mN), is the reasonable dimension and operational regime for capsule design and control.

4 Conclusions and future work

In this paper, we studied the modelling of a vibro-impact self-propelled capsule system moving in the small intestine. Our studies focused on exploring the dynamics of the system and its performance in terms of the average velocity and energy efficiency under various system and control parameters, such as the forcing frequency and magnitude of excitation, the natural frequency of the inner mass, the contact gap between the inner mass and the secondary spring, and the capsule’s radius and length. We also considered the capsule’s progression along an inclined intestine and its optimum design and control parameters.

Under the assumption that the intestinal tract fully contacts with capsule surface, the intestinal resistance exerted on the capsule can be modelled using hoop strain and stress. It was found that the resistance and its threshold become larger when the capsule’s size or its instantaneous velocity increases. We also found that strengthening the forcing magnitude of excitation can benefit the average velocity of the capsule, but will lead to low energy efficiency. Increasing the radius and length of the capsule could result in resistance enhancement, which can simplify its bifurcation pattern, enlarge the parametric regime of period-two motion, and decrease capsule’s average velocity and energy efficiency. However, if the magnitude of the driving force is sufficiently large, the capsule having a larger resistance can achieve a faster forward progression.

Our investigation on the natural frequency of the inner mass shows that, when the driving frequency is relatively lower than its natural frequency, successive grazing bifurcations will occur, and this will decrease the times of impact at each period but drastically increase the average velocity of the capsule. When the forcing frequency is chosen to be in the vicinity of the natural frequency, period doubling can be observed, which leads to sudden drops of average velocity and energy efficiency. As the forcing magnitude is increased, average velocity will be decreased at low forcing frequencies while be increased at high forcing frequencies (i.e. the frequency greater than the natural frequency). Our calculations also reveal that reducing the natural frequency of the inner mass can improve capsule’s average velocity. However, this will not affect the energy efficiency of the system.

The stiffness of the secondary spring and the contact gap between the inner mass and the secondary spring was studied under variation of forcing frequency. For a stiffer secondary spring, the capsule has a faster average velocity under a low driving frequency, while a slower progression when the driving frequency becomes high (i.e. the frequency greater than its natural frequency). The dynamics of the capsule is complicated under a prestressed secondary spring, leading to a small window of chaos and period-three motion when the forcing frequency is a branching parameter. When the gap is increased, the parametric regime of period-one motion can be enlarged, which can simplify the dynamics of the capsule. Our studies also indicate that the local maxima of the average velocities for different gaps can be obtained after each grazing bifurcation, and the capsule with \(g_1=3\) (mm) has the maximal average speed after its grazing bifurcation from period-one with two impacts to period-one motion with one impact. Furthermore, varying the contact gap cannot improve the energy efficiency of the system.

Our final study focused on the locomotion of the capsule along an inclined intestinal tract. As the magnitude of the driving force increases, the capsule can move forward on a slope with an inclined angle up to \(\gamma =0.35\) (rad). However, larger magnitude of the driving force will not help capsule’s forward progression, especially for a steeper slope, e.g. \(\gamma =0.35\) (rad). It was found that, along a steeper slope, the capsule always has a slower velocity due to gravity and insufficient resistance. To overcome gravity, the capsule with \(R_\mathrm{c}=4.2\) (mm) and the forcing magnitude, \(P_\mathrm{d}\in [13.9, 29.2)\) (mN), is a reasonable choice for locomotion control.

In conclusion, our numerical studies based on a pig small intestine with the radius of \(R_\mathrm{i}=3.9\) (mm) suggest the following optimum design and control parameters as a design guideline, capsule’s radius \(R_\mathrm{c}=4.2\) (mm) and length \(L=10\) (mm), forcing frequency \(\Omega >30\) (rad/s) and magnitude \(P_\mathrm{d}>15\) (mN), natural frequency of the inner mass \(\omega _n<25\) (rad/s), stiffness of the secondary spring \(k_1=4\) (N/m), and the gap between the inner mass and the secondary stiffness \(g_1=3\) (mm).

Future works include prototype design and fabrication, test rig design, and experimental testing of the capsule prototype. Design and fabrication of the capsule prototype will be based on the numerical studies in this paper, and an artificial intestinal environment will be built for experimental testing of the prototype. Research findings along this direction will be reported in a separate publication in due course.