Non-smooth predictive control for mechanical transmission systems with backlash-like hysteresis

Abstract

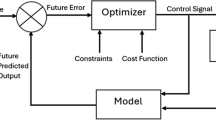
This paper proposes a non-smooth predictive control approach for mechanical transmission systems described by dynamic models with preceded backlash-like hysteresis. In this type of system, the work platform is driven by a DC motor through a gearbox. The work platform is represented by a linear dynamic sub-model connected in series with a backlash-like hysteresis inherent in gearbox. Here, backlash-like hysteresis is modeled as a non-smooth function with multi-valued mapping. In this case, the conventional model predictive control for such system cannot be implemented directly since the gradients of the control objective function with respect to control variables do not exist at non-smooth points. In order to solve this problem, a non-smooth receding horizon strategy is proposed. Moreover, the stability of predictive control of such non-smooth dynamic systems is analyzed. Finally, a numerical example and a simulation study on a mechanical transmission system are presented for validating the proposed method.

Appendices

Appendix 1

In the following, the proof of Theorem 3 will be presented.

For the convenience of analysis, it is supposed that

$$\begin{aligned} \mathbf{U}_1 (k)=\mathbf{U}(k)-\mathbf{D}(k). \end{aligned}$$

(43)

Based on formulae (1), (2), (12) and (22), $\mathbf{U}_1 (k)$ can be represented by

$$\begin{aligned} \mathbf{U}_1 (k)= & {} \left[ {{\varvec{\Lambda }}+\left( \tilde{\mathbf{h}}(k) \right) ^{T}{} \mathbf{F}_0 ^{T}{} \mathbf{QF}_0 \mathbf{h}(k)} \right] ^{-1} \nonumber \\&\Bigg \{{\varvec{\Lambda }} \mathbf{U}_1 (k-1)+\left( \tilde{\mathbf{h}}(k) \right) ^{T}{} \mathbf{F}_0 ^{T}{} \mathbf{Q}\nonumber \\&\times \Bigg [ {\mathbf{R}}(k+1)\mathbf{-G}y(k)+\mathbf{F}_\mathbf{0} \tilde{{\varvec{\upvarphi }}}(k)\mathbf{X}(k-1)\nonumber \\&-\mathbf{F}_\mathbf{1} \Delta \mathbf{X}(k-1)\Bigg ] \Bigg \}. \end{aligned}$$

(44)

It is known that, in receding horizon control strategy, only the first element of control vector, i.e., u(k) is implemented to the controlled system, the other control sequence, i.e., $u(k+1),\ldots ,$ and $u(k+N_u -1)$ are not implemented. Therefore, from (44), it is obtained that

$$\begin{aligned} u_1 (k)= & {} [1{\hbox { 0 }}\ldots \mathrm{0}]\mathbf{U}_1\nonumber \\= & {} \mathbf{d}_{\mathbf{11}} u_1 (k-1)+\mathbf{d}_{21} \left[ \mathbf{R}(k+1)\mathbf{-G}y(k)\right. \nonumber \\&\left. +\,\mathbf{F}_\mathbf{0} \tilde{{\varvec{\upvarphi }}}(k)\mathbf{X}(k-1)-\mathbf{F}_\mathbf{1} \Delta \mathbf{X}(k-1) \right] . \end{aligned}$$

(45)

Based on the definition of $\mathbf{F}_0 ,\mathbf{X}(k),{\tilde{{\varvec{\upvarphi }}}}(k),\mathbf{F}_\mathbf{1}$ and $\Delta \mathbf{X}(k-1)$, it leads to:

$$\begin{aligned}&{} \mathbf{F}_0 {\tilde{\varvec{\upvarphi }}}(k)\mathbf{X}(k-1)\nonumber \\&\quad =\left[ {{\begin{array}{cccccc} {s_{d,0} }&{} 0&{} \ldots &{} &{} 0 \\ {s_{d+1,1} }&{} {s_{d,0} }&{} \ldots &{} &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} &{} \vdots \\ {s_{L,L-d+2} }&{} {s_{L-1,L-d+3} }&{} \ldots &{} &{} {s_{L-N_u +1,L-N_u -d+1} } \\ \end{array} }} \right] \nonumber \\&\quad \times \left( {{\begin{array}{l} {\left( {1-\phi (k-1)} \right) \hat{{x}}(k-1)} \\ {\left( {1-\phi (k)} \right) \hat{{x}}(k)} \\ \vdots \\ {\left( {1-\phi (k+N_u -2)} \right) \hat{{x}}(k+N_u -2)} \\ \end{array} }} \right) \nonumber \\&\quad =\left( {{\begin{array}{l} {s_{d,0} z^{-1}\left( {1-\phi (k-1)} \right) } \\ {(s_{d+1,1} z^{-1}+s_{d,0} )\left( {1-\phi (k)} \right) } \\ \vdots \\ (s_{L,L-d+2} z^{-1}+s_{L-1,L-d+3} +\ldots \\ \quad +s_{L-N_u +1,L-N_u -d+1} z^{N_u -2})\\ \quad \left( {1-\phi (k+N_u -2)} \right) \\ \end{array}}} \right) \hat{{x}}(k)\nonumber \\&\quad ={\bar{\mathbf{F}}}_0 (z^{-1})\hat{{x}}(k) \end{aligned}$$

(46)

and

$$\begin{aligned}&{} \mathbf{F}_\mathbf{1} \Delta \mathbf{X}(k-1)\nonumber \\&\quad =\left[ {{\begin{array}{cccc} {s_{d,n_b } }&{} {s_{d,n_b -1} }&{} \ldots &{} {s_{d,1} } \\ {s_{d+1,n_b +1} }&{} {s_{d+1,n_b } }&{} \ldots &{} {s_{d+1,2} } \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ {s_{L,n_b +L-d} }&{} {s_{L,n_b +L-d-1} }&{} \ldots &{} {s_{L,L-d+1} } \\ \end{array}}}\right] \nonumber \\&\qquad \times \left( {{\begin{array}{l} {\Delta \hat{{x}}(k-n_b )} \\ {\Delta \hat{{x}}(k-n_b +1)} \\ \vdots \\ {\Delta \hat{{x}}(k-1)} \\ \end{array} }} \right) \nonumber \\&=\left[ {{\begin{array}{l} -s_{d,n_b } z^{-n_b -1}+(s_{d,n_b } -s_{d,n_b -1} )z^{-n_b }+\cdots \\ \quad +(s_{d,2} -s_{d,1} )z^{-2}+s_{d,1} z^{-1} \\ -s_{d+1,n_b +1} z^{-n_b -1}+(s_{d+1,n_b +1} -s_{d+1,n_b } )z^{-n_b }\\ \quad +\cdots +(s_{d+1,3} -s_{d+1,2} )z^{-2}+s_{d+1,2} z^{-1} \\ \vdots \\ -s_{L,n_b +L-d} z^{-n_b -1}+(s_{L,n_b +L-d} -s_{L,n_b +L-d-1} )\\ \quad \times z^{-n_b }+\cdots +(s_{L,L-d} -s_{L,L-d+1} )z^{-2}\\ \quad +s_{L,L-d+1} z^{-1} \\ \end{array} }} \right] \hat{{x}}(k) \nonumber \\&\quad ={\bar{\mathbf{F}}}_1 (z^{-1})\hat{{x}}(k). \end{aligned}$$

(47)

By substituting (46) and (47) into (45), it yields

$$\begin{aligned}&u_1 (k)=\mathbf{d}_{\mathbf{11}} u_1 (k-1)\nonumber \\&\quad +\mathbf{d}_{21} \left[ {\mathbf{R}(k+1)\mathbf{-G}y(k)+({\bar{\mathbf{F}}}_0 (z^{-1})-{\bar{\mathbf{F}}}_1 (z^{-1}))\hat{{x}}(k)} \right] .\nonumber \\ \end{aligned}$$

(48)

It is known that

$$\begin{aligned} y(k)=y_{m} (k)+e(k). \end{aligned}$$

(49)

where $y_{m} (k)$ is the output of system model, e(k) is the model error which is defined as $e(k)=y(k)-y_{m} (k)$.

For $\hat{{M}}_1 (z^{-1})$ is the model of linear sub-system, it leads to:

$$\begin{aligned} y_m (k)=\hat{{M}}_1 (z^{-1})\hat{{x}}(k). \end{aligned}$$

(50)

Then, substituting Eqs. (50) into (49) results in

$$\begin{aligned} y(k)=\hat{{M}}_1 (z^{-1})\hat{{x}}(k)+e(k). \end{aligned}$$

(51)

Afterward, substituting Eqs. (51) into (48) yields

$$\begin{aligned} u_1 (k)= & {} \mathbf{d}_{\mathbf{11}} u_1 (k-1)+\mathbf{d}_{21}\nonumber \\&\times \left[ \mathbf{R}(k+1)\mathbf{-G}\hat{{M}}_1 (z^{-1})\hat{{x}}(k)-\mathbf{G}e(k)\right. \nonumber \\&+\, \left. ({\bar{\mathbf{F}}}_0 (z^{-1})-{\bar{\mathbf{F}}}_1 (z^{-1}))\hat{{x}}(k) \right] . \end{aligned}$$

(52)

In the following, the proof will be implemented based on two cases, i.e.,

Case 1 if the system operates in linear zones, based on Eqs. (2), (25) and (43), Eq. (52) can be written as:

$$\begin{aligned}&u_1 (k)=\mathbf{d}_{\mathbf{11}} z^{-1}u_1 (k)\!+\!\mathbf{d}_{21} \left[ \mathbf{R}(k+1)\mathbf{-G}\hat{{M}}_1 (z^{-1})\right] \nonumber \\&\quad \left[ {\hat{{m}}_1 +(\hat{{m}}_2 -\hat{{m}}_1 )\tilde{w}(k)} \right] u_1 (k)\nonumber \\&\quad -\,\mathbf{G}e(k)+({\bar{\mathbf{F}}}_0 (z^{-1})-{\bar{\mathbf{F}}}_1 (z^{-1})\left[ \hat{{m}}_1\right. \nonumber \\&\quad \left. +\,(\hat{{m}}_2 -\hat{{m}}_1 )\tilde{w}(k) \right] u_1 (k)], \end{aligned}$$

(53)

namely,

$$\begin{aligned} u_1 (k)\!=\!\frac{1}{F(z^{-1})}[D_r (z^{-1})r(k\!+\!L)\!-\!M_2 (z^{-1})e(k)],\nonumber \\ \end{aligned}$$

(54)

where

$$\begin{aligned} F(z^{-1})= & {} \mathbf{d}_{21} \mathbf{G}\hat{{M}}_1 (z^{-1})\left[ {\hat{{m}}_1 +(\hat{{m}}_2 -\hat{{m}}_1 )\tilde{w}(k)} \right] \\&+\mathbf{d}_{21}({\bar{\mathbf{F}}}_1 (z^{-1})-{\bar{\mathbf{F}}}_0 (z^{-1}))\\&\times \left[ {\hat{{m}}_1 +(\hat{{m}}_2 -\hat{{m}}_1 )\tilde{w}(k)} \right] -\mathbf{d}_{\mathbf{11}} z^{-1}+1 \\= & {} \mathbf{d}_{21} \mathbf{G}G_m (z^{-1})+\mathbf{d}_{21} ({\bar{\mathbf{F}}}_1\\&(z^{-1})-{\bar{\mathbf{F}}}_0 (z^{-1}))\left[ {\hat{{m}}_1 +(\hat{{m}}_2 -\hat{{m}}_1 )\tilde{w}(k)} \right] \\&-\mathbf{d}_{\mathbf{11}} z^{-1}+1 , \end{aligned}$$

$M_2 (z^{-1})=\mathbf{d}_{21} \mathbf{G}$ and $D_{r} (z^{-1})y_{r} (k+L)=\mathbf{d}_{21} \mathbf{R}(k+1)$. Based on (43), it leads to

$$\begin{aligned} u(k)=u_{1} (k)+D(k). \end{aligned}$$

(55)

By considering Remark 1, (24)–(28) and (49)–(51), (54) can be written as:

$$\begin{aligned} u_1 (k)= & {} \frac{1}{F(z^{-1})-M_2 (z^{-1})G_m (z^{-1})}\nonumber \\&[D_r (z^{-1})r(k+L)-M_2 (z^{-1})y(k)]. \end{aligned}$$

(56)

Then, based on (24)–(29), (49)–(51) and (54), it leads to

$$\begin{aligned} y(k)= & {} \frac{G_{s} (z^{-1})D_{r} (z^{-1})r(k+L)}{F(z^{-1})+M_2 (z^{-1})\Delta \tilde{G}(z^{-1})}\nonumber \\= & {} \frac{G_{s} (z^{-1})G_{c} (z^{-1})D_{r} (z^{-1})r(k+L)}{1+G_{c} (z^{-1})M_2 (z^{-1})\Delta \tilde{G}(z^{-1})}. \end{aligned}$$

(57)

In terms of the small gain Theorem, note that the relation between (29) and (30). Then, it is known that the control system is stable if $G_{c} (z^{-1})$ and $P(z^{-1})$ are selected to satisfy

$$\begin{aligned}&\mathrm{sup}|G_c (z^{-1})||M_2 (z^{-1})||\eta (z^{-1})|\nonumber \\&\quad =\frac{{\hbox {sup}}|M_2 (z^{-1})||\eta (z^{-1})|}{\mathrm{inf}|P(z^{-1})|}<1,\hbox { and namely },\nonumber \\&\quad \times \mathrm{sup}|M_2 (z^{-1})||\eta (z^{-1})|<\mathrm{inf}|P(z^{-1})| \end{aligned}$$

(58)

Case 2 The control system works in memory zones.

In this case, it is known that:

$$\begin{aligned} u(k)=u(k-1). \end{aligned}$$

(59)

If (58) is satisfied to enable the control system to be stable in Case 1, the control system is also stable when the system works in memory zones.

Thus, the corresponding closed-loop control system can be stabilized if $\mathrm{sup}|M_2 (z^{-1})||\eta (z^{-1})|<\mathrm{inf}|P(z^{-1})|$.

End of proof. $\square$

Appendix 2

• Step 1: Given $\varepsilon >0$;

• Step 2: Calculate the Clarke sub-gradient of x(k) with respect to u(k), i.e., estimate $\tilde{h}_1 (k)$ in (22);

• Step 3: Calculate the Clarke sub-gradient of J(k) with respect to u(k), i.e., $\partial J_{k}^{j_2 } (u(k))$ where $j_2 =1,2,\cdots ,t$, and t is a bounded natural number;

• Step 4: Calculate $u_{j_2 } (k)$ based on Eq.(23);

• Step 5: If $J(k)\le t_1 \varepsilon ,t_1 \in (0,1)$, and $u(k)=u_{j_2 } (k)$, it goes to step 7; otherwise, go to step 6;

• Step 6: Let $u(k)=u_{j_3} (k)$, where $u_{j_3}(k)$ enables J(k) to reach its minima;

• Step 7: Let $k=k$ +1, and go to step 2.

Appendix 3

In this appendix, the procedure to deduce (22) is shown as follows.

Substituting (15) into (12) leads to:

$$\begin{aligned} J(k)= & {} \frac{1}{2}[\mathbf{R}(k+1)-\mathbf{G}y(k)-\mathbf{F}_\mathbf{0} \mathbf{h}(k)\mathbf{U}(k)\nonumber \\&+\mathbf{F}_\mathbf{0} \mathbf{h}(k)\mathbf{D}(k) +\mathbf{F}_\mathbf{0}{\tilde{\varvec{\upvarphi }}}(k)\mathbf{X}(k-1) \nonumber \\&-\,\mathbf{F}_1 \Delta \mathbf{X}(k-1)]^{\mathbf{T}}{} \mathbf{Q}[\mathbf{R}(k+1)- \nonumber \\&\mathbf{G}y(k)-\mathbf{F}_\mathbf{0} \mathbf{h}(k)\mathbf{U}(k)+\mathbf{F}_\mathbf{0} \mathbf{h}(k)\mathbf{D}(k)\nonumber \\&+\mathbf{F}_\mathbf{0} {\tilde{\varvec{\upvarphi }}}(k)\mathbf{X}(k-1)-\,\mathbf{F}_1 \Delta \mathbf{X}(k-1)]\nonumber \\&+\Delta \mathbf{U}(k)^{\mathbf{T}} {\varvec{\Lambda }} \Delta \mathbf{U}(k) \end{aligned}$$

(60)

Thus, the corresponding Clarke sub-differential of J(k) with respect to u(k) can be obtained by:

$$\begin{aligned}&\partial _{u(k)} J(k) \nonumber \\&\quad =-\left( {{\tilde{\mathbf{h}}}(k)} \right) ^{T}{} \mathbf{F}_0 ^{T}{} \mathbf{Q}\big [ \mathbf{R}(k+1)\nonumber \\&\qquad -\mathbf{G}y(k)-\mathbf{F}_\mathbf{0} \mathbf{h}(k)\mathbf{U}(k)+\,\mathbf{F}_\mathbf{0} \mathbf{h}(k)\mathbf{D}(k)\nonumber \\&\qquad +\,\mathbf{F}_\mathbf{0} {\tilde{\varvec{\upvarphi }}}(k)\mathbf{X}(k-1)-\mathbf{F}_1 \Delta \mathbf{X}(k-1) \big ]+\,{\varvec{\Lambda }} \Delta \mathbf{U} .\nonumber \\ \end{aligned}$$

(61)

Based on Theorem 1 and (61), it leads to:

$$\begin{aligned}&-\left( {{\tilde{\mathbf{h}}}(k)} \right) ^{T}{} \mathbf{F}_0 ^{T}{} \mathbf{Q}\big [ \mathbf{R}(k+1)-\mathbf{G}y(k)\nonumber \\&\quad -\mathbf{F}_\mathbf{0} \mathbf{h}(k)\mathbf{U}(k)+\,\mathbf{F}_\mathbf{0} \mathbf{h}(k)\mathbf{D}(k)\nonumber \\&\quad +\,\mathbf{F}_\mathbf{0} {\tilde{\varvec{\upvarphi }}} (k)\mathbf{X}(k-1)-\mathbf{F}_1 \Delta \mathbf{X}(k-1) \big ]\nonumber \\&\quad +{\varvec{\Lambda }} \Delta \mathbf{U}=0. \end{aligned}$$

(62)

Namely, (22) is obtained