Abstract
An accurate means of predicting erosion rates is essential to improve the predictive capability of breach models. During breach growth, erosion rates are often determined with empirical equations. The predictive capability of empirical equations is governed by the range for which they have been validated and the accuracy with which empirical coefficients can be established. Most empirical equations thereby do not account for the impact of material texture, moisture content, and compaction energy on the erosion rates. The method presented in this paper acknowledges the impact of these parameters by accounting for the process of dilation during erosion. The paper shows how, given high surface shear stresses, the erosion rate can be quantified by applying the principles of soil mechanics. Key is thereby to identify that stress balance situation for which the dilatency induced inflow gives a maximum averaged shear resistance. The effectiveness of the model in predicting erosion rates is indicated by means of three validation test cases. A sensitivity analysis of the method is also provided to show that the predictions lie within the range of inaccuracy of the input parameters.
Similar content being viewed by others
1 Introduction
Once earthen dams or levees have breached high flow velocities cause for the breach to grow in lateral direction until the breach flow drowns (see Fig. 1) (Morris 2011; Morris et al. 2008; Visser 1998). The process of lateral widening is characterized by erosion and subsequent undercutting of the near vertical side slopes of the breach by the breach flow (Morris 2011) (see Fig. 1).
Photo taken of the breach widening process during the breach experiment in The Zwin, the Netherlands (Visser 1998)
Once a geotechnical failure of the side slope initiates, high flow velocities through the breach rapidly remove the failed soil material as was observed during the IMPACT field experiments (Morris 2011). The breach widening rate is therefore given by the rate of lateral erosion. The process of erosion of steep slopes due to high shear stresses is not yet fully understood. Despite this, erosion rates are often predicted with empirical equations like the Erosion Equation. The Erosion Equation linearly relates the lateral erosion rate to an excess shear stress via a soil erodibility parameter (Morris et al. 2008). Applying the Erosion Equation is problematic as no accurate means of predicting the soil erodibility and critical shear stress exist. Morris et al. (2008), Hanson and Hunt (2007) and Al-Riffai and Nistor (2010) noted that the soil erodibility depends on material texture, moisture content, and compaction energy. Erosion relationships that do not account for these parameters struggle to provide reliable predictions over the range of embankment types and conditions (Morris et al. 2008). Van Rhee (2010) and Bisschop et al. (2016) identified that the erosion sensitivity of dilatant soils depends on the initial porosity with respect to the critical porosity, and the hydraulic conductivity of soil. Bisschop et al. (2016) noted that under high shear stress conditions the rate of erosion E of horizontal beds of dilatant sediments is proportional to the bed shear stress \(\tau _0\) [\(\hbox {N}/\hbox {m}^{2}\)] according to: \(E=\alpha \tau _0^{\beta }\). Here \(\beta\) has a range of 0.25–0.75. The unknown power dependence of the erosion rate on the surface shear stress further adds to the inaccuracy of predictions of lateral erosion rates. Besides the erosion equations, other sediment pick-up formulas have been developed for flow velocities up to 3 m/s (Winterwerp et al. 1992; Mastbergen and Van den Berg 2003; Van Rhee 2010) which provide improved predictions for the pick-up flux under high shear stresses (van Rijn 1984; Bisschop et al. 2016). However, these relations are predominantly empirical and have been developed for horizontal beds. The range of validity of these methods is implicitly limited to the range of experimental testing conditions. Not all soil material subjected to erosion in a breach is fully saturated at the onset of erosion. Dissipation of the effective stresses during infiltration of water may thereby make the erosion process time dependent (Verruijt 2001; Al-Riffai and Nistor 2010). Capturing all these influences in empirical models would be challenging. Hence, a process-based approach is welcomed to better predict lateral erosion rates.
This paper outlines a new and accurate method for predicting breach widening rates. This new method is based on relating the rate of erosion to the exchange of mass and momentum during dilation of soil. Flow-induced shear stresses acting on the breach sides easily exceed 10 \(\hbox {N}/\hbox {m}^{2}\). The breach thereby grows due to live scour effects as no equilibrium transport conditions are reached. When dilatant soils are subjected to high shear stresses, the erosion process is no longer characterized by the pick-up of individual particles but by the continuous shear failure of layers of soil. Over the depth over which the bed shear stresses exceed the shear strength, momentum is transferred to the acceleration of the bed (Iverson et al. 1997; Iverson 2000; Tamotsu 2009; Takahashi 1981). For soil layers to shear over each other, soil needs to dilate. The associated increase in pore volume is accommodated by an inflow of water which is driven by the pressure gradient over the bed. The reduction in pore water pressures in the bed gives an increase in effective stresses and an increase in shear resistance. Material types, soil permeability, compaction efforts, and moisture content influence the process of dilation and therefore also the rate of erosion (Morris et al. 2008; Hanson and Hunt 2007; Van Rhee 2007, 2010). When the degree of compaction is high, the initial porosity and hydraulic conductivity are small, and the degree of dilation needed for soil to shear is high. Together with the low hydraulic conductivity, this gives rise to high negative pore water pressures inside the soil. Consequently, the dilatancy induced shear resistance is higher than for poorly compacted soils, giving lower erosion rates (Van Rhee 2010). Similarly, a rough material texture gives a high critical porosity at which the particles are able to shear over each other.
The constitutive equations that describe the process of dilation, given in Sect. 2, provide an improved understanding of the process of erosion of dilatant soils observed during breach widening. During erosion, the exchange of momentum between soil and water was found to converge to a state for which the average dilatancy induced shear resistance is optimum. The outlined process-based method provides accurate predictions for the pick-up rate of soil subjected to high shear stresses for various geometries. The correspondence between the predicted and measured data is presented in Sect. 3 for two cases of breach widening and a case of erosion of a horizontal bed. A discussion of the results and the conclusions are given in Sect. 4 of this paper.
2 Methodology
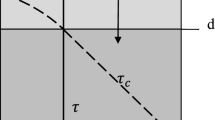
This section outlines the constitutive equations that describe the process of dilatancy of soils subjected to high shear stresses by fast-flowing water. Shear stresses acting on a soil surface are transferred to the deeper layers. Particles mobilize over the depth d [m] over which shear stresses exceed the shear resistance (Tamotsu 2009). The maximum shear resistance \(\tau _c\) [\(\hbox {N}/\hbox {m}^{2}\)] of soil is given by the Mohr–Coulomb failure criterion
where \(\sigma '\) [\(\hbox {N}/\hbox {m}^{2}\)] denotes the effective stress, \(\phi\) is the angle of internal friction, and C [\(\hbox {N}/\hbox {m}^{2}\)] is the cohesion of the bed. Shear deformation of dilatant soils is accommodated by an increase in pore volume (see Fig. 2). The pressure gradient required to accommodate the associated inflow of water gives a decrease in pore pressures in the soil, an increase in effective stresses \(\sigma '\) [\(\hbox {N}/\hbox {m}^{2}\)], and an increase in shear resistance.
Dissipation of the low pore pressures by the inflow of water induces continuous shallow shear failures of soil, resembling the process of erosion.
In the following sections the constitutive equations that describe this process are derived for the case of a flow past a near-vertical wall. The x-direction thereby coincides with the main flow direction past the x, z-plane. The z-coordinate has been taken parallel to the soil-water interface pointing upwards, and the positive y-direction is pointing into the soil (see Fig. 3). The positive velocity vectors u [m/s], v [m/s] and w [m/s], respectively, coincide with the positive x-, y- and z-coordinate directions.
2.1 Mass balance equation
For the case of incompressible particles and incompressible water the mass balance equation for water in a porous system is given by
where n denotes the porosity, and subscript \(_{w}\) refers to water. Similarly, the mass balance equation for solid particles in a porous medium is given by
where subscript \(_{p}\) refers to particles. Adding Eqs. 2 and 3 gives
The last three terms in Eq. 4 give a change in porosity due to volumetric strain and equal \(\frac{1}{1-n}\frac{\partial n}{\partial t}\) (Verruijt 2006). The terms \(n(u_{w}-u_{p})\), \(n(v_{w}-w_{p})\) and \(n(w_{w}-w_{p})\), respectively, denote the specific discharges \(q_{x}\) [m/s], \(q_{y}\) [m/s] and \(q_{z}\) [m/s]. Substituting the expressions for the specific discharges in Eq. 4 gives
Flow and gravity induced shear stresses acting on the x, z-plane are transferred in y-direction. The thickness of shear layers is assumed small compared to the characteristic length scales of the surface on which the shear stresses act. This allows for the problem of erosion to be regarded as the problem of displacement of a soil plane in the y-coordinate direction. To better describe the continuous displacement of the soil plane, a coordinate system was defined by \(y = \eta - ct\) (Jensen and Finlayson 1980; Verruijt 2006), where c [m/s] is the rate of displacement of the x, z-surface in the y-coordinate direction. No significant spatial variations in shear stress are assumed to occur in the x- and z-coordinate directions. The depth integrated mass balance equation for water (see Eq. 2) now becomes
Over the depth d the increase in porosity is assumed to be constant (Verruijt 2006; Van der Schrieck 2006). This is in line with the conclusions of Casagrande (1936) who observed that samples subjected to large deformations reach the same porosity. It is also a requirement for integrating the momentum balance equations, as will be discussed in Sect. 2.2. At depth d, shear stresses equal the shear strength. Over the short time duration required to remove a soil layer with depth d, denoted by \(t = d/c\), the degree of deformation of the soil skeleton below the failure depth d is assumed negligible compared to the deformation over d. Under this assumption \(v_{w}|_{\eta =d} = v_{p}|_{\eta =0} = 0\). Dilation is thereby assumed to be solely accommodated by the inflow of water through the soil surface given by the x, z-plane. Integrating Eq. 6 over \(\eta\) from \(\eta = 0\) to \(\eta = d\) gives
Rewriting Eq. 3 in terms of a moving coordinate system and integrating it from \(\eta = 0\) to \(\eta = d\) similarly gives the depth integrated mass balance equation for the particles
whereby it has been assumed that \(v_{p}|_{d}=0\). The depth integrated mass balance equation of the total porous medium similarly follows from rewriting and integrating Eq. 5 leading to
Here \(n|_{\eta =d}\) has been assumed to equal the initial porosity \(n_{0}\), whereas \(n|_{\eta =0}\) is assumed to equal the critical porosity of fully dilated material \(n_{\text {loose}}\) (Van der Schrieck 2006).
2.2 Momentum balance equations
The general momentum balance equations for a flow in soil consist of the sum of the momentum balance equations of the particles and those of water. Below the momentum balance equations for an infinitely long slope are given whereby stress gradients and gradients in momentum exchange in the x- and z-direction are neglected. The bed displaces due to dilation in the negative y-coordinate direction (see Fig. 4). The momentum balance equations in, respectively, the x- and z-coordinate direction are now given by
and
Here \(\rho _{p}\) [\(\hbox {kg}/\hbox {m}^{3}\)] and \(\rho _{w}\) [\(\hbox {kg}/\hbox {m}^{3}\)], respectively, denote the density of the soil particles and the density of water, g [m/s\(^{2}\)] denotes the acceleration constant, \(K_{s}\) [m/s] is the saturated hydraulic conductivity of the bed, \(\tau _{yx}'\) [\(\hbox {N}/\hbox {m}^{2}\)] is the shear stress component in the x-coordinate direction, and \(\tau _{yz}'\) [\(\hbox {N}/\hbox {m}^{2}\)] is the shear stress component acting in the z-coordinate direction. The terms \(\gamma _{w}\) [\(\hbox {N}/\hbox {m}^{3}\)] and \(\gamma _{s}\) [\(\hbox {N}/\hbox {m}^{3}\)], respectively, denote the specific weight of water and that of soil. The momentum balance equation describing the exchange in momentum in the y-coordinate direction via the pore water pressures is given by
where P [\(\hbox {N}/\hbox {m}^{2}\)] denotes the pore water pressure. An integrable form of the momentum balance equation in the x-coordinate direction is obtained by substituting Eqs. 2 and 3 in Eq. 10 under the assumption that n is spatially constant over d, which leads to
Prior to integrating Eq. 13 the fixed coordinate system has been replaced by the moving coordinate system \(\eta = y - ct\), giving
The same procedure of substituting the mass balance equations and transforming the fixed coordinate system into a moving coordinate system has been applied to the momentum balance equations in the z- and y-coordinate directions (see Eqs. 11 and 12), giving
and
When acceleration terms are temporarily ignored, the momentum balance equations show that shear stresses uniformly acting on a soil surface are translated to the deeper soil layers without change (Takahashi 1981). This is indicated by the dotted line in Fig. 4, which represents the distribution in \(\tau _{\eta x}|_{\eta =0}\) with depth. Over the depth over which the shear stresses exceed the shear resistance, denoted by \(\tau _{c}|_{\eta = d}\), the momentum balance needs to be enforced causing for the soil particles to accelerate and dilate. The process of dilation leads to, acceleration of soil particles, a reduction in pore water pressure and an increase in shear resistance. Casagrande (1936) noted that samples subjected to large deformations reach the same porosity (Van Rhee 2010). Based on this observation, dilatancy has been assumed to give a uniform increase in pore spaces over the interval \(\mathopen {[}0,d\mathclose {)}\) (see Fig. 4). Consequently, \(v_{w}\) [m/s] and \(v_{p}\) [m/s] are linearly distributed over \(\eta\) and \(v_{w}|_{\eta =d} = v_{p}|_{\eta =0} = 0\).
Over the depth d the velocity component of the particles in the x-coordinate direction is assumed to equal the velocity component of the pore water in the x-coordinate direction. Similarly, the velocity components of the pore water in the z-coordinate direction is expected to equal the velocity components of the particles in the z-coordinate direction. Integrating Eqs. 14, 15 and 16 under these conditions from \(\eta = 0\) to \(\eta = d\) give for the momentum balance equation in the x-coordinate direction
For the momentum balance equation in the z-coordinate direction this becomes
Due to dilation, the pore water flow in y-direction is in opposite direction of the movement of the particles in \(\eta\)-direction. Consequently, a Darcy friction term was included. The momentum balance equation in the \(\eta\)-coordinate direction now becomes
The mass balance equations given by Eqs. 7 and 8 state that at boundary (\(\eta = 0\)), \(v_{w}|_{\eta =0} = c\frac{n_{\text {loose}}-n_0}{n_{\text {loose}}}\) and \(v_{p}|_{\eta =0} = -c\frac{n_{\text {loose}}-n_0}{1-n_{\text {loose}}}\). Here \(n_{\text {loose}}\) corresponds with the porosity of a critically dilated bed at \(n|_{\eta =0}\) and \(n_0\) corresponds with the in-situ porosity given by \(n|_{\eta =d}\). The porosity \(n\approx n_{\text {loose}}\). Substituting these relationships in the momentum balance equations gives the following integrated momentum balance equation in the x-coordinate direction expressed in terms of the rate of displacement of the boundary c [m/s].
The momentum balance equations describing the exchange of momentum in, respectively, the z- and \({\eta }\)-coordinate directions now become
and
The second term on the second row of Eq. 22 equals the total contribution of the friction experienced by the flow over d. \(v_{w}\) and \(v_{p}\) linearly decrease over \({\eta }\) and are 0 at depth d. The total head loss experienced by the porous flow due to friction is consequently half the displacement rate of the surface, denoted by the 2 in the denominator. The rate of displacement of the soil body c is of the order of mm/s. The depth d is of the order of mm, and for sands the hydraulic conductivity is of the order of mm/s. Under these conditions, the effects of friction far outweigh the effects of the advective acceleration, or \(cd/K_{s}>> c^{2}\). Equation 22 gives the pressure at the failure depth \(P|_d\). The effective stress at depth d follows from the soil pressure minus the water pressure. Assuming a negligible impact of the acceleration terms in Eq. 22 now gives the following expression for the effective stresses at depth d.
The failure depth is given by the depth at which the shear stress equals the Mohr–Coulomb failure criterion given by Eq. 1 (Verruijt 2001). Soil failure initiates when the shear stresses equal the shear strength. Substituting Eq. 23 into Eq. 1 and setting the Mohr–Coulomb failure criterion at depth d [m] equal to the shear stress at depth d [m], given by Eq. 20, leads to the following expressions for the stability of the soil.
and
Equations 24 and 25 relate the failure depth d [m] to the rate of displacement of the boundary c [m/s]. As c increases d decreases.
Breach widening resembles the erosion of a submerged (near) vertical soil surface. This follows from setting \(\alpha = 0\), \(\tau _{\eta z}|_{\eta =0} = 0\), and \(\tau _{\eta x}|_{\eta =0} > 0\). Hence, the flow is only assumed to induce a surface shear stress in the x-coordinate direction. The flow velocity component \(u_{w} = u_{p}\) is thereby approximated by the shear velocity (Schiereck 2004) which is given by
where the fraction serves to preserve the correct sign. The surface shear stress in the z-coordinate direction is 0. However, due to the steep slope, gravity initiates dilation of the material. The lateral erosion rate of the wall follows from the sum of the effects of gravity induced shear stress and the effects of the flow induced shear stress. The first solution, denoted by \(c_z\) [m/s], is given by the vertical force balance whereby the dilatancy induced effective stresses give a shear resistance \(\tau _c|_{\eta }\), which must equal the effects of the weight of the soil \(\sigma _g|_{\eta }\) (Van Rhee 2010; Van der Schrieck 2006) (see Fig. 5).
The solution for this problem follows from Eq. 25 for \(\tau _{\eta z}|_{\eta =0} = 0\), and \(w_{p} = w_{w} = 0\). For this specific case, the depth d drops out of the equation and the rate of boundary displacement becomes purely a function of the hydraulic conductivity \(K_{s}\), the specific weights of the soil \(\gamma _{s}\) and water \(\gamma _{w}\), and the difference between the initial porosity \(n_0\) and critical porosity \(n_{\text {loose}}\). Under these conditions Eq. 25 becomes.
The contribution of the surface shear stress to the lateral erosion rate follows from the horizontal momentum balance equation whereby \(\tau _{\eta x}|_{\eta =0} > 0\). Due to the presence of a horizontal shear stress component acting on a vertical soil surface, a failure depth d [m] needs to be defined. The lateral erosion rate is related to the rate of inflow of water into soil. A high rate of inflow requires a high pressure gradient. The corresponding low pore water pressures give a high shear resistance and a low failure depth. Hence, the c is inversely related to the failure depth d. The average excess shear stress available for accelerating the sheared soil layers depends on the average resistance against shearing over d. As the failure depth and erosion rate are inversely related, a failure depth d exists for which the average dilatancy induced shear resistance is maximum, and the momentum available for accelerating the particles is minimum. This situation corresponds with a maximum in effective stresses, averaged over the failure depth. The linear decrease in velocity profiles \(v_{w}\) [m/s] and \(v_{p}\) [m/s], associated with the spatially constant rate of dilation, is given by
Substituting Eq. 28 in Darcy’s law and twice integrating with respect to \(\eta\) and dividing by d gives the average shear induced drop in pore water pressure over d [m]. For \(\frac{dP}{d\eta }|_{\eta =d} = 0\) and \(P|_{\eta =0} = 0\) the integral of the drop in pore water pressure, denoted by \(P_f\) [\(\hbox {N}/\hbox {m}^{2}\)], is given by.
Effective stresses are given by the soil pressure minus the water pressure. The failure depth averaged contribution of pore water pressures to the increase in effective stress, and hence shear resistance, follows from substituting \(\eta = d\) and dividing by d. The failure depth averaged effective stress is now given by
The depth d for which the averaged effective stress is maximum follows from including the effects of \(c_z\) (see Eq. 27). The shear resistance provided by the gravity induced dilation equals \(\tau = (\gamma _{s}-\gamma _{w})\text {cos}(\alpha )d\), for \(\alpha = 0\) (see Eq. 27). The constant inflow thereby also induces an additional exchange of momentum between the flow and the soil. Accounting for the effects of \(c_z\) in Eq. 24 gives for \(\alpha = 0\)
where the contribution of \(c_z\) [m/s] on the shear resistance is accounted for in the first term of the denominator. Substituting Eq. 31 in Eq. 30 gives a relationship for the average effective stress as a function of the rate of displacement of a vertical soil surface due to erosion c [m/s]. Figure 6 shows this relationship for a shear stress of \(\tau _0 = 100\) \(\hbox {N}/\hbox {m}^{2}\) and \(K_{s} = 1E-4\) m/s, for a non-cohesive dilatant soil.
As illustrated by Fig. 6 a maximum average effective stress is found for a specific value of the boundary displacement rate c [m/s]. This maximum corresponds with a minimum in momentum available for the acceleration of soil particles at the surface and resembles the most stable situation.
3 Results
Here, the hypothesis is tested that the erosion rate corresponds with the bed displacement rate for which the average shear resistance is optimum. Since more data are available on the erosion of flat beds than the erosion of steep slopes the method was first validated against available data on the erosion of a flat surface due to high flow velocities, whereby \(\alpha = 90\) and \(c_{y} = 0\). The method is also validated against two cases on lateral breach growth. The deposit of material in the breach due to sudden failure of undermined embankment material is thereby assumed to have a negligible effect on breach growth rate due to rapid removal of the material by the high flow velocities through the breach (Morris 2011). Results of a sensitivity analysis are also presented to indicate the sensitivity of the erosion rate prediction for the model input.
3.1 Validation against high speed erosion experiments on a horizontal bed
Here, erosion rate predictions are validated against the dataset published by Bisschop (2018), who performed high speed erosion tests on a flat bed (\(\alpha = 90\) degrees)for various types of sand in order to derive a pick-up relation. Based on observations Bisschop (2018) related the observed bed shear stress to the occurrence of turbulent sweeps. Here, this method has not been adopted as the bed shear stresses are assumed to resemble the Reynolds averaged bed shear stresses. These follows from extrapolating the Reynolds shear stress distribution outside the laminar sub layer to the bed. According to the Reynolds decomposition, turbulent motions in the flow are split in a mean and fluctuating part. The Reynolds shear stress follows from the average of the product of the turbulent fluctuations in horizontal and vertical direction. The impact of turbulent sweeps is consequently already accounted for in the determination of the bed shear stress. By relating the erosion process to the occurrence of turbulent sweeps the impact of the sweeps would be accounted for twice. Here is therefore assumed that the impact of the turbulent sweeps has implicitly been accounted for via the Reynolds averaged bed shear stress.
For the Geba and Zilverzand sand the properties are given in Table 1 (Bisschop 2018), where the d10, d50, and d90 denote the particle sizes for which respectively 10%, 50%, and 90% of the particles are smaller, Cu denotes the coefficient of uniformity, and nmin and nmax refer to the minimum and maximum porosity.
The hydraulic conductivity of the sand beds was determined with the Kozeny–Carman Equation (see Eq. 34) after substituting the Kozeny–Carman constants. The friction angle was set at 35 degrees. Based on the values for the bed shear stress \(\tau _{\eta x}|_{\eta = 0}\), the critical porosity nloose = nmax and initial porosity \(n_0 = n_{min}\), provided by Bisschop (2018), that boundary displacement rate c was determined for which the dilatancy induced shear resistance is maximum. For a flat bed (\(\alpha = 90\) degrees) the failure depth follows from
and the shear resistance follows from Eq. 30. The boundary displacement rate c [m/s] was translated into a pick-up flux by multiplying it with the density of the bed given by \(\rho _{w} n_0+(1-n_0)\rho _{p}\). The match between the data and the predictions is given in Figs. 7 and 8. The volatile nature of the erosion process induced high measurement errors in the data. Bisschop (2018) estimated the errors in bed shear stress to be between 10% and 80%, and errors in erosion rate predictions to be up to 70% for low pick-up fluxes and between 20% and 40% for high pick-up fluxes. The results, nevertheless, clearly show that the general trend of the predictions is in line with the measurements.
3.2 Validation of the erosion predictions for vertical walls
3.2.1 Sensitivity analysis
A sensitivity analysis was performed on the method to evaluate a range in acceptable predictions given the accuracy of the input parameters. The results of this analysis are given in Table 2 for the case of lateral erosion past a vertical side wall. The wall shear stress \(\tau _{\eta x}|_{\eta = 0}\) was thereby varied between 20 and 100 \(\hbox {N}/\hbox {m}^{2}\). Input parameters were changed individually by 5% in either direction with respect to the input parameters given in the table. The sensitivity is given by the average ratio between the new prediction and the original prediction.
The effect of the slope angle \(\alpha\) was also investigated. For a decrease in steepness of the side slope of the breach by 5.5 deg. the erosion rate decreased by \(5\%\). The hydraulic conductivity was kept constant when the sensitivity of the initial porosity \(n_0\) was determined. The hydraulic conductivity is, however, dependent on the porosity (see Eq. 34). Consequently, the effects of changing the initial porosity on the erosion rates are expected to be higher. The change in density of water \(\rho _{w}\) here implies the effect of accounting for a mixture flow over the bed. The density of water present in or flowing through the porous media has not been altered in this analysis.
3.3 Validation against the Zwin breach experiment
In 1994, a full scale breach experiment was executed in the Zwin Channel, a tidal inlet at the Dutch Belgian border. Inside the tidal channel a sand dam had been constructed for the purpose of a breach experiment. The sand dam had a crest height \(H_c\) of 2.6 m, a crest width \(W_c\) of 8 m, a landside slope gradient \(1:S_L = 1:3\) (V:H) and a waterside slope gradient \(1:S_W = 1:1.6\) (V:H). (see Table 3). Approximately 8.5 minutes after the start of the experiment a full breach had formed with steep breach sides and the breach started to widen (Visser 1998). The angle of the side slopes has been estimated at 75 degrees (see Fig. 1), which was used to validate the process based method for predicting lateral erosion rates. During the breach widening stage, and prior to the drowning of the breach flow, surface flow velocities through the breach reached between 4.2 and 4.4 \(\hbox {m}/\hbox {s}\) (Visser 1998). Over a time interval of 15 minutes the breach width B [m] increased at a constant rate from 8 m to 28 m giving an average breach widening rate of 0.022 \(\hbox {m}/\hbox {s}\) (Visser 1998). The shear stress acting on the side walls at this velocity is approximately 0.7 times the bed shear stress (Chow 1959) and has been estimated with
where the hydraulic radius R [m] has been approximated by the water depth which has been estimated at 1.8 m. The Manning coefficient N was estimated to be 0.025 \(\hbox {s}/\hbox {m}^{1/3}\). Substituting the observed range of flow velocities in Eq. 33 gives a range of shear stresses between 62–68 \(\hbox {N}/\hbox {m}^{2}\).
During the Zwin breach experiment the sand dam was constructed from both the original Zwin sand and construction sand. The density of the sand particles has been estimated at 2650 \(\hbox {kg}/\hbox {m}^{3}\). The porosity of the constructed sand dam was estimated at \(n_0 = 0.37\). Of the original Zwin sand the \(d_{10} = 0.155\) mm. For the construction sand the \(d_{10} = 0.215\) mm. Since these sand fractions are finer than 3 mm, the hydraulic conductivity could be estimated from the Kozeny–Carman equation given by
where \(C_k\) is the Kozeny Carman constant which was set to \(8.3\times 10^{-3}\) (Chapuis and Aubertin 2003), g [\(\hbox {m}/\hbox {s}^{2}\)] is the gravitational constant, and \(\nu\) [\(\hbox {m}^{2}\)/s] is the kinematic viscosity of water. As the hydraulic conductivity of soil is determined by the smallest particles, the \(d_{10}\)-value of the Zwin sand was used to determine the hydraulic conductivity of the levee material. Substituting the porosity \(n_0\) and the \(d_{10}\) value of the Zwin sand in Eq. 34 gives \(K_{s} = 2.5\times 10^{-4}\) \(\hbox {m}/\hbox {s}\). The internal friction angle was estimated at 35 deg. and the critical porosity \(n_{\text {loose}}\) was estimated to be 0.46 (Van der Schrieck 2006). For \(\alpha = 15\), Fig. 9 depicts the erosion rate as a function of the shear stress. The figure also depicts the depth d at which the shear stresses equal the shear resistance. As can be seen, the depth far exceeds the diameter of the particles.
For the given input parameters the erosion rate per breach side is expected to vary between 0.011 m/s and 0.0113 m/s (see Fig. 9). The breach widening rate is given by twice the erosion rate as erosion occurs on both sides of the breach. This gives a breach widening rate 2c of between 0.022 m/s and 0.023 m/s which is in good agreement with the measured rates of erosion during the experiment. The contribution of the momentum balance in the z-coordinate direction to the breach widening rate is thereby \(1.7E-3\) m/s indicating that the surface shear stress dominates the erosion process. For an initial porosity of \(n_0 = 0.4\), the predictions of the widening rate would become approximately, respectively, 0.028 and 0.029 m/s which is 14% higher than predicted but of the same order of magnitude. This error of 14% does indicate the need for detailed information on the initial porosity of the material.
Schematization of the breach experiments with the parameters given by Table 3
3.4 Validation against the ARS breach widening tests
A large-scale breach widening test performed by Hunt et al. (2005) on a homogeneous levee constructed of silty sand formed the second validation test case. The levee was 1.3 m high, and had a crest width of 1.8 m. The landside and waterside slope gradients were 1:3 (V:H). Prior to testing, a 0.3 m wide notch was cut over the full height of the test levee and backfilled with sand. The water level in the test basin was increased until the sand in the breach notch overtopped. This caused for rapid removal of the sand and for the breach to start widening. During the experiment, the water level upstream of the levee was kept at a constant elevation such that flow velocities through the breach remained constant. The average wall shear stress exerted on to the breach side slopes was 20 \(\hbox {N}/\hbox {m}^{2}\) (Hunt et al. 2005).
These levees contained a significant degree of fines. The \(d_{10}\) was estimated from the distribution of fines at 2 \(\mu\)m. The density of the particles was 2670 \(\hbox {kg}/\hbox {m}^{3}\). The initial porosity was obtained from the dry specific weight and the grain density and was \(n_0 = 0.35\). The critical porosity was estimated at \(n_{\text {loose}} = 0.46\). Equation 34 now gives a hydraulic conductivity of \(K_{s} = 3.31 \times 10^{-8}\) \(\hbox {m}/\hbox {s}\). For \(\alpha = 0\) and \(\tau = 20\) \(\hbox {N}/\hbox {m}^{2}\), the lateral erosion rate c for which the average shear resistance is maximum is \(c = 1.02 \times 10^{-4}\) m/s (see Fig. 11, which corresponds with a breach widening rate of \(2.04 \times 10^{-4}\) m/s. The prediction is thereby in agreement with the measured breach widening rate of \(2c = 2 \times 10^{-4}\) m/s. Figure 11 thereby also shows that the depth over which the shear failures occur exceeds the particle diameter of the material in the bed.
4 Discussion
This paper provides a method for quantifying lateral erosion rates. The method is based on the constitutive mass and momentum balance equations that describe the dilation process. Predictions show a significant decrease in erosion rates decrease with a decrease in initial porosity or hydraulic conductivity. The initial porosity of material influences the hydraulic conductivity, the density of the bed material, and the degree of dilation required to loosen the soil. This corresponds with observations by Roberts et al. (1998); Van Rhee (2010) and Hunt et al. (2005) who noted that the porosity has a significant influence on the erosion rate. Figures 11 and 9 thereby show that the depth d over which shear failures occur and particles are accelerated is significantly larger than the diameter of the soil particles, indicating that erosion indeed describes the shear failure of layers of particles. The predictions for the pick-up flux under high flow velocities are in line with the general trend observed in the data of Bisschop (2018). For both the Zwin as the ARS breach widening tests, the breach widening rate predictions are in accordance with the data. It should, however, be noted that for the breach widening tests no accurate information was available on the critical porosity or hydraulic conductivity. Nevertheless, given the level of accuracy of the Kozeny Carman equation (Chapuis and Aubertin 2003), the uncertainty of the prediction of the critical porosity, and the sensitivity for the prediction on these parameters, the predictions of the erosion rates are in good agreement with the measured values. The method has thus far only been validated against cases whereby sand or silty sand eroded. Consequently it is only possible to state that sand or silty sand converges to a state for which the average shear resistance is optimum when it is subjected to high shear stresses. For this state the exchange of momentum between the flow and the sand is minimum. Extension of the method to other soil types, unsaturated porous media, and other stress configurations is recommended (Al-Riffai and Nistor 2010). To facilitate further validation, the hydraulic conductivity, porosity, and critical porosity of the construction material should be determined when performing erosion and breach experiments. It should thereby be noted that the process of high speed erosion differs significantly from the process of erosion at low velocities, which is governed by the pick-up of individual particles (Van Rhee 2010). Scaled model tests hence may not provide an accurate representation of the breach process.
5 Conclusions
This paper provides a process based explanation of how dilation affects the erosion process of sand during lateral erosion by high velocity flows. The lateral erosion rates follow from analyzing those conditions for which the dilatancy induced shear resistance of sand is maximum. The predicted pick-up rates are in agreement with measurements for both horizontal beds and vertical slopes. Further validation of the method for other soil types and stress orientations is highly recommended.
Availability of data and material
Not applicable.
References
Al-Riffai M, Nistor I (2010) Impact and analysis of geotechnical processes on earthfil dam breaching. Nat Hazards 55:15–27
Bisschop F (2018) Erosion of sand at high flow velocities. PhD thesis, Delft University of Technology
Bisschop F, Miedema SA, Visser PJ, Keetels GH, Van Rhee C (2016) Experiments on the pickup flux of sand at high flow velocities. J Hydraul Eng 142(7):04016013.1–0401603.11. https://doi.org/10.1061/(ASCE)HY.1943-7900.0001142
Casagrande A (1936) Characteristics of cohesionless soils affecting the stability of earth fills. J Boston Soc Civ Eng 23:257–276
Chapuis R, Aubertin M (2003) Predicting the coefficient of permeability of soils using the Kozeny–Carman equation. Tech. rep., Département des génies civil, géologique et des mines
Chow VT (1959) Open-channel hydraulics. McGraw-Hill, New York
Hanson GJ, Hunt SL (2007) Lessons learned using laboratory JET method to measure soil erodibility of compacted soils. Appl Eng Agric 23(3):305–312
Hunt S, Hanson G, Cook K, Kadavy K (2005) Breach widening observations from earthen embankment tests. Am Soc Agric Eng 48(3):1115–1120
Iverson RM (2000) Landslide triggering by rain infiltration. Water Resour Res 36(7):1897–1910. https://doi.org/10.1029/2000WR900090
Iverson RM, Reid ME, LaHusen RG (1997) Debris-flow mobilization from landslides. Annu Rev Earth Planet Sci 25(1):85–138. https://doi.org/10.1146/annurev.earth.25.1.85
Jensen OK, Finlayson BA (1980) Solution of the transport equations using a moving coordinate system. Adv Water Resour 3:9–18. https://doi.org/10.1016/0309-1708(80)90014-7
Mastbergen DW, Van den Berg JH (2003) Breaching in fine sands and the generation of sustained turbidity currents in submarine canyons. Sedimentology 40(4):625–637
Morris M (2011) Breaching of earth embankments and dams. PhD thesis, Open University
Morris M, Hanson G, Hassan M (2008) Improving the accuracy of breach modelling: why are we not progressing faster? J Flood Risk Manag 1(3):150–161. https://doi.org/10.1111/j.1753-318X.2008.00017.x
Roberts J, Jepsen R, Gotthard D, Lick W (1998) Effects of particle size and bulk density on erosion of quartz particles. J Hydraul Eng 124(12):1261–1267
Schiereck GJ (2004) Introduction to bed, bank and shore protection. Delft University Press, Engineering the interface of soil and water
Takahashi T (1981) Debris flow. Annu Rev Fluid Mech 13(1):57–77. https://doi.org/10.1146/annurev.fl.13.010181.000421
Tamotsu T (2009) A review of Japanese Debris flow research. Int J Erosion Control Eng 2(1):1–14. https://doi.org/10.13101/ijece.2.1
Van Rhee C (2010) Sediment entrainment at high flow velocities. J Hydraul Eng 136(9):572–582
van Rijn LC (1984) Sediment pick-up functions. J Hydraul Eng 110(10):1494–1502. https://doi.org/10.1061/(ASCE)0733-9429(1984)110:10(1494)
Van der Schrieck GLM (2006) Dredging technology CT5300. Delft University of Technology
Van Rhee C (2007) Erosion of granular sediments at high flow velocities. In: Hydrotransport 17, conference on the hydraulic transport of solids, pp 551–560
Verruijt A (2001) Soil mechanics. Delft University of Technology. http://geo.verruijt.net/
Verruijt A (2006) Offshore soil mechanics. Delft University of Technology, Delft
Visser PJ (1998) Breach growth in sand-dikes. PhD thesis, Delft University of Technology, Netherlands
Winterwerp JC, Bakker WT, Mastbergen DR, van Rossum H (1992) Hyperconcentrated sand-water mixture flows over erodible bed. J Hydraul Eng 118(11):1508–1525. https://doi.org/10.1061/(ASCE)0733-9429(1992)118:11(1508)
Funding
This research was performed as part of an NWO TTW Project (Project Number 13861).
Author information
Authors and Affiliations
Contributions
Not applicable.
Corresponding author
Ethics declarations
Conflict of interest
There are no conflicts of interests and no competing interests.
Code availability
Custom code.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
van Damme, M. A process-based method for predicting lateral erosion rates. Nat Hazards 107, 375–394 (2021). https://doi.org/10.1007/s11069-021-04587-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-021-04587-y