Abstract
An efficient approach to ocean–iceberg modelling provides a means for assessing prospects for seasonal forecasting of iceberg distributions in the northwest Atlantic, where icebergs present a hazard to mariners each spring. The stand-alone surface (SAS) module that is part of the Nucleus for European Modelling of the Ocean (NEMO) is coupled with the NEMO iceberg module (ICB) in a “SAS-ICB” configuration with horizontal resolution of 0.25°. Iceberg conditions are investigated for three recent years, 2013–2015, characterized by widely varying iceberg distributions. The relative simplicity of SAS-ICB facilitates efficient investigation of sensitivity to iceberg fluxes and prevailing environmental conditions. SAS-ICB is provided with daily surface ocean analysis fields from the global Forecasting Ocean Assimilation Model (FOAM) of the Met Office. Surface currents, temperatures and height together determine iceberg advection and melting rates. Iceberg drift is further governed by surface winds, which are updated every 3 h. The flux of icebergs from the Greenland ice sheet is determined from engineering control theory and specified as an upstream flux in the vicinity of Davis Strait for January or February. Simulated iceberg distributions are evaluated alongside observations reported and archived by the International Ice Patrol. The best agreement with observations is obtained when variability in both upstream iceberg flux and oceanographic/atmospheric conditions is taken into account. Including interactive icebergs in an ocean–atmosphere model with sufficient seasonal forecast skill, and provided with accurate winter iceberg fluxes, it is concluded that seasonal forecasts of spring/summer iceberg conditions for the northwest Atlantic are now a realistic prospect.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Icebergs have long been a risk to shipping in the northwest Atlantic (Hill 2006), with records of collisions and sinkings stretching back into the seventeenth century (Bigg 2016). While the period of maximum risk is largely restricted to only a few months of the spring and early summer, the combination of greater volume of shipping and the introduction of marine technology enabling near all-weather travel increased the number of major iceberg incidents in the northwest Atlantic dramatically through the late nineteenth century, until the tragic sinking of RMS Titanic in 1912 sparked the formation of the International Ice Patrol (IIP). This has the combined mission of observing sea ice and icebergs in the northwest Atlantic, warning shipping of ice hazards, and understanding ice–ocean processes (Murphy and Cass 2012). The IIP issues daily ice and iceberg charts, with short-term warning services, and keeps a long-term record of iceberg locations and particularly the number of icebergs reaching waters south of 48°N in the northwest Atlantic, the area of greatest risk to shipping travelling between Europe and northeast North America.
The iceberg risk varies enormously from year to year, however, with some years recording no icebergs passing across 48°N while others record well in excess of 1000 (Bigg 2016), and generally higher numbers have been counted south of 48°N since the 1980s. Bigg et al. (2014) showed that variable calving rates from Greenland largely explain the observed variability in annual counts of icebergs drifting south of 48°N (henceforth “I48N”), using both an ocean–iceberg model and control system modelling of over a century of iceberg records to independently lead to this conclusion. Given this finding, we here explore the extent to which spring/summer iceberg distributions in the northwest Atlantic are related to early season southward flux of icebergs in the Labrador Current. Specifying the upstream iceberg flux in the vicinity of Davis Strait from engineering control theory, we use advanced ocean forecasting and iceberg trajectory model technology to assess the potential for seasonal forecasting of iceberg risk in the northwest Atlantic.
Models of iceberg drift have been used for some time for short-term forecasting of individual icebergs (e.g. Smith 1993) or study of climatological iceberg distributions (Bigg et al. 1997). Recently, Marsh et al. (2015) took the basic model system of Bigg et al. (1997) and developed a model to represent the drift and melting of icebergs in the polar oceans as an interactive option in the Nucleus for European Modelling of the Ocean (NEMO), named ICB (for ICeBerg). The NEMO framework is widely used throughout Europe, and the Met Office adopted NEMO around 2010. The Met Office has developed seamless prediction systems that use NEMO for daily forecasts in Forecasting Ocean Assimilation Model (FOAM), for seasonal forecasts in Global Seasonal Forecasting (GloSea5) and for climate prediction in the latest in the Hadley Centre family of climate models (HadGEM3). Here, FOAM and ICB are used to explore iceberg distributions in the northwest Atlantic and their predictive potential. We are using “best-estimate” ocean and atmospheric analyses as inputs rather than seasonal forecasts, so the results provide an upper bound on the predictive potential for seasonal timescales.
To facilitate efficient investigation, ICB is forced in offline mode with surface ocean currents, temperatures and height from FOAM, and corresponding winds. While icebergs can feed back on the ocean state and circulation on multi-decadal timescales (Marsh et al. 2015), such feedbacks will be small at seasonal timescales, justifying the offline mode developed here. ICB is therefore coupled with the stand-alone surface (SAS) module that is part of the NEMO framework, a model option subsequently termed SAS-ICB. We configure SAS-ICB at a resolution of 1/4° that is compatible with the current global FOAM configuration.
For this exploration we chose three recent, and highly contrasting, years in terms of their observed iceberg density and southward extent, namely 2013–2015. The basic driving forces sending icebergs south from Greenland are the ocean currents, principally the subpolar gyre and particularly the Labrador Current, in which most icebergs are embedded, and the near-surface winds. The influence of winds on iceberg trajectories is twofold. Wagner and Eisenman (2017) recently showed that winds can strongly influence iceberg drift, but also that winds strongly influence melt rates through the standard parameterization of wind-driven wave erosion, which dominates iceberg melting in the open ocean. In the same study, stronger ocean currents are shown to carry icebergs further afield before fully melting.
Both the local winds and the Labrador Current vary, to a large extent with the North Atlantic Oscillation (NAO) (Wang et al. 2016, and references therein). Anomalous strong northwesterly and westerly winds in the winters of 2013/2014 and 2014/2015, respectively, led to extensive cooling across much of the subpolar gyre (Grist et al. 2016; Duchez et al. 2016). Given this variability, we further explore the links to anomalous winds, currents and surface temperatures, investigating whether more icebergs arrive with anomalously cold water and/or whether icebergs persist longer, in larger numbers, in cold years. Iceberg conditions in the northwest Atlantic are thus closely linked to the climate state and have the potential to be forecast at seasonal timescale, given recent advances in winter forecasting (e.g. Scaife et al. 2014).
We emphasize again here that our study addresses the prospects for seasonal forecasting rather than the actual forecasts themselves. The paper is organized as follows. In Sect. 2 we provide a brief description of SAS-ICB, the method for specifying iceberg influx in the upstream Labrador Current just south of Davis Strait, model forcing (surface currents, temperatures, height and winds), and the IIP data we use for evaluating our simulations. In Sect. 3, we present recent observations of iceberg distributions and fluxes, as used in model evaluation, followed by the results of model experiments to investigate the sensitivity of simulated iceberg distributions to upstream flux and environmental conditions. Concluding with Sect. 4, we summarize our findings and consider the prospects for seasonal prediction.
2 Method and data
2.1 SAS-ICB: model description
The stand-alone surface (SAS) module of NEMO provides a framework for efficiently testing surface flux schemes and sea ice models (http://www.nemo-ocean.eu/About-NEMO/News/New-release-of-2012-developments). For the current study, we extended SAS to run with ICB, in the new model variant SAS-ICB. We configure SAS-ICB on the ORCA025 grid (the same configuration as FOAM), with a global horizontal resolution of 0.25° on a tripolar mesh, with 1442 and 1021 grid cells in model longitude and latitude, respectively (Madec 2008). The time step is 24 min (60 time steps per day).
ICB runs with default parameters (see Marsh et al. 2015). A calving rate file specifies iceberg fluxes at arbitrary locations—normally the termini of glaciers or ice shelves, but here in the upstream Labrador Current (see Sect. 2.3). Icebergs in ICB are treated statistically as point collections of icebergs across 10 size categories, using a size distribution introduced by Bigg et al. (1997), which has persisted in widespread use through the later developments of Martin and Adcroft (2010) and Marsh et al. (2015). Assuming that this distribution is appropriate to the Greenland Ice Sheet (GrIS) calving flux, the small percentage reaching the upstream Labrador Current should appropriately represent the number of large icebergs anticipated to survive by this point. All icebergs are represented as cuboids, with a fixed width/length ratio of 1.5, following Bigg et al. (1997) and subsequent iceberg modelling studies.
The ORC025 configuration of SAS-ICB runs on 96 cores of a local high-performance computing system at the National Oceanography Centre, Southampton. ICB provides a wide range of iceberg diagnostics. In particular, individual iceberg positions are recorded daily, along with the iceberg dimensions and local sea surface temperature (SST). Trajectory data are post-processed to obtain the results presented in Sects. 3.2 and 3.3. In comparing simulations with IIP data, we count model icebergs as individuals, regardless of their size category. In the case of icebergs surviving to 48°N, these are typically in the largest three size categories, represented by a single berg. Counting model icebergs that move south across 48°N, it is possible that we occasionally double-count icebergs that move back north across 48°N and return south again, although this is unlikely to substantially influence our results.
2.2 NARMAX predictions
Bigg et al. (2014) used the Nonlinear Auto-Regressive Moving Average with eXogenous input (NARMAX) system identification model to separate the annual GrIS discharge signal in I48N data from post-calving ocean–atmospheric influences, over 1900–2008. The NARMAX model is “trained” using I48N data, but the discharge predictions are based on three independent variables: the NAO-index; GrIS mass balance; mean SST for the Labrador Sea. NARMAX thus provides the discharge, or calving flux, appropriate to icebergs drifting south towards 48°N in a given year, with no knowledge of the specific I48N count in that year. This approach was subsequently extended to monthly analysis (Zhao et al. 2016). In the present study, this NARMAX model was extended to 2015. Further details of the NARMAX predictions are provided in Supplementary Material.
For icebergs calved from Greenland to reach 48°N, dominant lag times are around 6–10 months (see Figure S3 of Supplementary Material). Relating this 4-month spread to arrival at 48°N typically in the period March–June, all icebergs would have calved in the previous September. Alternatively relating this spread to the observed April/May peak in arrival at 48°N, icebergs are inferred to calve during the previous June–December. In summary, the NARMAX fluxes for iceberg arrival at 48°N in a given year relate to calving during the second half of the previous year, centred on autumn.
Over the twentieth century, decadal means of GrIS iceberg discharge inferred by Bigg et al. (2014) were found to vary in the range 96–659 km3 year−1. A small fraction of this calved flux reaches the northern Labrador Current around January–February, where we specify it as an influx (see Sect. 2.3). Our estimates for the three simulated years are as follows: 7.3 km3 year−1 (2013); 865.8 km3 year−1 (2014); 652.4 km3 year−1 (2015).
2.3 Model forcing
To force SAS-ICB, we specify the following oceanographic and meteorological variables:
-
Oceanographic variables from FOAM: daily-mean surface fields of current, temperature, salinity and sea surface height.
-
Atmospheric variables from v5 of the Drakkar Forcing Set (DFS5, Dussin et al. 2016): zonal and meridional components of wind at 10 m, temperature and humidity at 3 m (all 3-hourly); daily-mean net shortwave and longwave radiation; monthly mean rainfall and snowfall rates.
FOAM is an operational ocean forecasting system run at the Met Office each day, providing global analyses and 6-day forecasts of the three-dimensional ocean and sea ice state (Blockley et al. 2014). Observational data from various platforms are assimilated into the NEMO model using a 3DVar data assimilation scheme (Waters et al. 2015). The assimilated data include: in situ and satellite SST data; satellite altimeter sea surface height (SSH) data; satellite sea ice concentration data; and in situ profiles of temperature and salinity from various platforms including Argo, XBTs, CTDs, moored buoys and marine mammals. As well as providing short-range forecasts, the FOAM analysis is used to initialise the ocean component of coupled seasonal predictions in the GloSea5 system (MacLachlan et al. 2015). The FOAM data used here are from the near real-time operational system. The DFS5 forcing is specified in the absence of the weather forecasts used to force FOAM, which were not available to us.
Iceberg fluxes are a further key aspect of model forcing. With considerable uncertainty in the details of upstream iceberg distribution, an idealized forcing strategy was specified. In baseline experiments, we release an ensemble of icebergs in the 1° × 1° square 61–62°W, 59–60°N, at a specified rate during January or February, with zero flux thereafter. Our release location is close to that used in other studies of Greenland iceberg drift (e.g. Wagner and Eisenman). Based on the spread of lag times of around 6–10 months for icebergs calved from Greenland to reach 48°N and the range/peak of spring arrival times (see Sect. 2.1), initial fluxes in January or February infer a transit timescale from Greenland to the upstream Labrador Current of 1–6 months.
We vary the influx as follows. To a baseline flux of 10 km3 year−1, representing multi-year icebergs from Greenland and those from elsewhere, we add 2.5% of monthly flux, F, equivalent to the annual NARMAX flux. The monthly flux is simply calculated as the annual flux expressed in a single month; hence, the annual flux is multiplied by 12 to obtain the monthly equivalent flux. This small fraction (2.5%) is consistent with the limited number of icebergs that reach the Labrador Current, several months after calving plus melting en route, and is based on previous experience with NEMO-ICB (Marsh et al. 2015). We thus obtain the total fluxes applied in January or February, F tot, that are presented in Table 1.
In additional sensitivity experiments, we distribute the 2014 and 2015 flux 1° onshore or offshore of the default starting longitude, across 62–63°W and 60–61°W, respectively. Finally, to isolate the influence of variable currents, SST and winds on iceberg distributions, we take the 2000–2008 average of 271 km3 year−1 (Bigg et al. 2014) and apply this as a February influx (preferred over January, based on initial sensitivity experiments)—as for variable influx (see Table 1). All experiments are undertaken for each of 2013–2015 and are summarized in Table 2.
2.4 IIP data
The International Ice Patrol (IIP) publishes and archives daily charts of iceberg observations (http://www.navcen.uscg.gov/?pageName=iipCharts&Archives). In a pragmatic approach, we digitize charts published for the 15th day of each month, January–December, and sum these to obtain a cumulative total number of icebergs per 1° grid square, as a basic metric of iceberg distribution for that year. Good coverage is available for the years 2009 onwards, including the three study years, so we apply this analysis to 2009–2015.
2.5 Model and evaluation system
The proto-forecast system is summarized in Fig. 1, indicating in simple terms how SAS-ICB is forced, including the NARMAX process, and the outputs that are related to available IIP observations.
3 Results
3.1 Recent observations of iceberg distributions and fluxes, and prevailing oceanographic/meteorological conditions
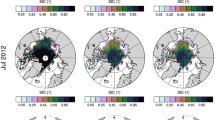
Figure 2 shows IIP iceberg distributions for 2009–2015, colour-coded for cumulative number per 1° grid square, sampling the 15th day of each month. This metric indicates considerable year-to-year differences in the extent and concentration of icebergs in the region, and correspondingly large year-to-year differences in the number of icebergs observed crossing 48°N. In Fig. 3, we show the number of icebergs observed crossing 48°N, monthly over 2009–2015 (Fig. 3a) and annually over 1900–2015 (Fig. 3b). The monthly I48N counts are highly variable from year to year, as in Fig. 2, with clear spring/summer peaks in 2009 (May), 2012 (May), 2014 (April/May) and 2015 (April), in contrast to near-zero values throughout 2010, 2011 and 2013. This is consistent with strong interannual–decadal variability in the annual I48N count over the longer period.
Paying particular attention to the ocean surface and meteorological conditions that influence icebergs in the Labrador Current during the critical months of February–May, Fig. 4 shows the corresponding anomalies (relative to a common reference period 1981–2010) for SST, sea level pressure (SLP), and wind speed, for the study years 2013–2015. In the northwest Atlantic, February–May 2013 was notable for anomalous warmth (with SST anomalies around 1 °C) and positive SLP anomalies, which favoured anomalous southerly winds. In contrast, February–May 2014 featured negative SST anomalies of around − 4 °C in Davis Strait and around − 2 °C in the Labrador Current, negative SLP anomalies across subpolar latitudes, and anomalously strong northwesterly winds across the Labrador Sea, while February–May 2015 brought SST and SLP anomalies similar to 2014, but with more climatologically typical winds. Taken together, iceberg and ocean/atmosphere observations suggest that heavier iceberg conditions are associated with colder surface temperatures and stronger northwesterly winds.
3.2 Sensitivity of simulated iceberg distributions to upstream flux
Here we present the results of the “VAR” experiments, comparing simulations to the IIP distributions (Fig. 2) and the I48N counts (Fig. 3). To first illustrate the full trajectory datasets, which we sample for diagnostics to more directly compare with observations or for statistical analysis of iceberg conditions, Fig. 5 shows daily positions for 2013–2015, colour-coded for day-of-year. Trajectories from January starts (Fig. 5a–c) and February starts (Fig. 5d–f) are shown separately.
The day-of-year diagnostic increases along trajectories from 0 to 30 (early January to early February) up to around 200 (late July) in 2014 and 2015, with earlier final dates in 2013. Icebergs clearly advect in a broadly southward direction in all experiments, remaining close to the Labrador coast in 2013, while moving substantial distances offshore in 2014 and 2015. Movement offshore is more extensive for initial iceberg fluxes in January. Large numbers of icebergs drift south of 48°N in 2014 and 2015, resulting in a widespread distribution of icebergs across the Grand Banks from around day 120 (early May). Differences between the years (January or February initial fluxes) are primarily a consequence of the considerable differences between initial iceberg fluxes.
For direct comparison with the IIP observations, in Fig. 6 we plot the simulated iceberg distributions for each experiment, sampled and colour-coded as in Fig. 2. Again apparent are large differences between the experiments. Very low concentrations are obtained in 2013, with much higher concentrations in 2014 and 2015. We obtain broadly good agreement with observations, better with January upstream iceberg fluxes in 2013 (Fig. 6a) and with February fluxes in 2014 (Fig. 6d) and 2015 (Fig. 6f). As in the observations, highest concentrations, exceeding 100 icebergs per 1° grid square, are obtained for 2014 (Fig. 6d). The relatively poor agreement with observations in 2013 indicates that we may have underestimated the upstream iceberg influx for that year, although erroneous ocean/atmosphere forcing could also contribute to the limited iceberg extent.
Simulated iceberg distributions, 2013–2015, colour-coded for cumulative number per 1° grid square (sampling as for IIP data—see Fig. 1): a, c, e January starts; b, d, f February starts
Averaged in 1° grid squares, but now sampling all trajectory points in Fig. 5, mapped statistics of advective timescale for iceberg drift, iceberg size (thickness) and local SST are presented in Figs. 7, 8 and 9. To explain the tendency for smaller and larger icebergs to, respectively, drift offshore or remain in the Labrador Current (Fig. 8), consider the momentum balance for an iceberg of mass M:
where f is the Coriolis parameter, and drag forces, \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\tau }_{\text{a}} \), \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\tau }_{\text{o}} \), \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\tau }_{\text{i}} \), for atmosphere, ocean and sea ice, respectively, a “wave radiation” force, \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{\text{r}} \), and a pressure gradient force, \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{\text{p}} \), are formulated as follows:
given iceberg width W, length L, submerged draught, D = (ρ/ρ o)T, thickness T = F + D (for freeboard F), sea ice thickness T i, and wave amplitude a. The vectors \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{\text{a}} \), \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{\text{o}} \) and \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{\text{i}} \) correspond to surface wind, surface ocean current and sea ice motion, respectively; η is the sea surface height. The parameters c a,v, c a,h, c o,v, c o,h and c i,v are drag coefficients parameterizing stresses between icebergs and the atmosphere, the ocean and sea ice, respectively, separately treating vertical and horizontal stresses between icebergs and wind or current.
As Fig. 6, colour-coded for day of year
As Fig. 6, colour-coded for thickness
As Fig. 6, colour-coded for sea surface temperature, indicating the − 1.5 °C isotherm with the thick white line
For steady iceberg drift, and dividing through by M, (1) can be re-written:
The four frictional and external force terms in (2) are thus functions of iceberg dimensions, as follows:
-
Atmospheric drag is a function of WF and LW
-
Ocean drag is a function of WD and LW
-
Sea ice drag is a function of W
-
Wave radiation force is a function of LW/(L + W)
Ocean drag and the wave radiation force tend to dominate atmospheric and sea ice drag, with atmospheric drag proportionately more important for small icebergs (Bigg et al. 1997). For small icebergs, compared to larger icebergs, the wave radiation force is also proportionately more important than ocean drag, which is more likely to be oriented with the geostrophic flow. Given these size dependencies, large icebergs will follow more geostrophic trajectories. This explains why small icebergs tend to escape the near-geostrophic Labrador Current and drift into the interior of the Labrador Sea, while large icebergs, remaining in the boundary current, dominate the iceberg flux past Newfoundland.
Considered together, mean thickness and local SST indicate that small icebergs melt in waters warmer than 2 °C, in the interior of the Labrador Sea, while large icebergs, with much greater thermal inertia, eventually melt quickly in waters warmer than 10 °C, beyond the outer Grand Banks. Icebergs are clearly most concentrated and persistent in the very cold waters of the Labrador Current, where SST in winter and early spring ranges from the freezing point of − 1.8 °C to around 2 °C. We indicate an approximate sea ice edge in Fig. 9 with the − 1.5 °C isotherm, slightly above the freezing point for seawater. In the model, icebergs do not interact directly with sea ice, but are indirectly affected, to a limited extent, through the effects (of sea ice) on wind stress, ocean currents and surface temperature. Consistent with the climate state for 2013–2015 (Fig. 4), mean local SST experienced by icebergs is relatively higher in 2013 (Fig. 9a, b) compared to 2014 (Fig. 9c, d) and 2015 (Fig. 9e, f)—indicated by the extent of the sea ice edge. SST anomalies—whether independent of, or related to, iceberg melting—may contribute to year-to-year differences in iceberg distributions and the I48N count, an issue we re-visit in Sect. 3.3.
Next, to address the timing of iceberg drift into the region of heaviest shipping and offshore activity, we sample the full trajectory dataset to obtain the number of icebergs crossing 48°N, I48N. Figure 10 shows monthly counts, in simulations with iceberg fluxes prescribed in January (blue bars) and February (green bars), and observed (red bars), for each year. Confirming our findings with the day-of-year diagnostic (Fig. 7), it is clear that very few icebergs drift south of 48°N in 2013, in both observations and VAR13Jan, with no such icebergs counted in VAR13Feb. In contrast, high values for I48N are observed and simulated for 2014 and 2015, with a clear April peak in 2015, best simulated in the VAR15Feb experiment; we obtain an unrealistic March peak in the VAR15Jan experiment. Likewise, the 2014 observations are best reproduced in the VAR14Feb experiment.
Finally, we consider sensitivity to start position, by shifting 1° onshore or offshore, relative to the default starting position, the prescribed February iceberg fluxes at 60°N. Figure 11 shows monthly counts for the three starting positions, again compared to observations, for 2014 (Fig. 11a) and 2015 (Fig. 11b). Overall, the simulated I48N statistics are somewhat degraded for both onshore and offshore starting positions. We therefore conclude that the most realistic I48N values are obtained for upstream iceberg fluxes specified in January 2013, February 2014 and February 2015, at the default longitude, in the main Labrador Current.
As Fig. 10, for prescribed February iceberg fluxes at 60°N, at the default longitude, shifted 1° on/offshore, and observed: a 2014; b 2015
3.3 Sensitivity of simulated iceberg distributions to environmental conditions
We isolate the secondary influences of variable environmental conditions with the “FIX” (climatological iceberg flux) experiments, for which differences in iceberg distributions are related only to anomalous winds, currents and temperatures. Figure 12 shows simulated iceberg distributions and mean day-of-year, for each year. In spite of specifying identical initial fluxes, differences are evident between the three years, although considerably smaller than with the iceberg fluxes for the correct year. In FIX13Feb, icebergs tend to remain more concentrated near the boundary, and limited numbers drift south of 48°N (Fig. 12a), compared to FIX14Feb (Fig. 12c) and FIX15Feb (Fig. 12e). The day-of-year diagnostic further indicates variations in transit time. On average, icebergs reach 48°N off Newfoundland at around day 150 (early June) in 2013 and 2014 (Figs. 12b, d), compared to day 120 (early May) in 2015 (Fig. 12f), and progress most slowly eastward of 50°W in 2013.
To further highlight differences between the three FIX experiments, Fig. 13 shows the simulated I48N diagnostics (blue bars) alongside the observed counts (red bars). It is again evident that substantially more icebergs drift south of 48°N in 2014 and 2015, compared with 2013. Also clear is the earlier peak in iceberg numbers in 2015, compared with 2014. Evidently then, environmental conditions reinforced the heavier iceberg conditions observed in 2014 and 2015.
It is intuitive that more/earlier icebergs coincide with cold conditions, but does anomalously cold water arrive with the icebergs, or do they persist longer in an already cold local environment? More intriguing is the extent to which icebergs influence their environment and hence melting rate. The extent to which icebergs contribute to local cooling via the latent heat flux of fusion may be estimated as follows. In a year of high iceberg concentration, such as 2014, consider 100 km3 of icebergs (about 40% of the total influx specified in January or February) melting over 1 month. Given the latent heat of fusion, 334 × 105 J kg−1, and average iceberg density, 850 kg m−3, the associated heat demand from the upper ocean is 100 × 109 × 334 × 105 × 850 = 2.84 × 1019 J, which over 4 months (e.g. February–May) equates to a flux of 2.75 × 1012 W. If we further consider that the icebergs melt in a convoluted area comprising the Labrador Current and part of the inner and outer Grand Banks, encompassing roughly 5° × 5° or ~ 250,000 km2, this equates to a surface heat flux of 11 Wm−2, although this heat flux will be distributed across a depth range that corresponds to the sub-surface melting. Locally and temporally, the heat demand by melting icebergs may be much higher.
How does this compare with local air–sea heat flux anomalies, in explaining anomalies in February–May averaged SST that locally range ± 2 °C (Fig. 4)? Figure 14 shows anomalies of net air–sea heat flux averaged over February–May, for 2013–2015. Across the region of iceberg melting, where the climatological net heat flux is close to zero, year-to-year anomalies are in the range ± 20 W m−2. Larger anomalies are located further offshore in the central Labrador Sea, where large amounts of heat are lost to the atmosphere. Returning to the region of iceberg melting, we conclude that the cooling associated with iceberg melting during February–May is comparable in magnitude to the local air–sea heat flux anomaly.
More indirectly, melting icebergs may freshen the upper ocean to a considerable extent. Climatological melt rates in the Grand Banks region of 1–10 cm year−1 (Martin and Adcroft 2010; Marsh et al. 2015) likely increase by an order of magnitude in years of high iceberg concentration, such as 2014 and 2015. The majority of this freshwater input will occur in late spring, implying monthly freshwater inputs of up to 25 cm (per month) during February–May, comparable to the local air–sea freshwater flux associated with excess precipitation in the region, at this time of the year. In terms of density flux, these freshwater fluxes are similar in magnitude to the local surface heat fluxes. Melting icebergs may therefore promote upper ocean stratification across the region in spring. For a given surface layer heat loss, direct to the atmosphere or due to iceberg melting, the temperature of a shallower surface layer will fall more rapidly. Stratification thus promotes lower surface layer temperatures.
In summary, the combined effects of local cooling and a more stratified surface layer due to iceberg melting are consistent with the negative SST anomalies along the Labrador Current and across the Grand Banks (Fig. 4) averaged for February–May of 2014 and 2015, coincident with high iceberg concentrations in these years (Fig. 2).
4 Conclusions and discussion
In the northwest Atlantic, icebergs are a major hazard for shipping around the Grand Banks, to the east and south of Newfoundland, where trans-Atlantic shipping lanes are located. On 6 April 2017, various media outlets cited IIP warnings that an unusually high number of icebergs (~ 450) were affecting the shipping lanes, causing considerable inconvenience to several large cargo ship operators. To our knowledge, earlier advance warnings were not issued for the 2017 season. In the current study, we demonstrate the potential for substantially earlier warnings. We have used an offline iceberg model, SAS-ICB, to simulate iceberg drift and distributions in the northwest Atlantic during three contrasting years, 2013–2015. SAS-ICB is between 1 and 2 orders of magnitude more computationally efficient, compared to its fully coupled counterpart, NEMO-ICB, taking around 6 h to simulate iceberg drifts for a given year with SAS-ICB, configured globally. SAS-ICB is thus ideal for multiple short-term forecasts, and for undertaking the extensive tests necessary to refine forecasts, experimenting in particular with the prescription of early-season iceberg fluxes, here specified in the upstream Labrador Current.
We have evaluated our simulations using digitized charts of icebergs that are observed during regular aircraft surveillance. The model is forced with daily oceanographic data (surface currents, temperatures and height) from the Met Office ocean forecast system and 3-hourly winds. We post-process up to several thousand individual iceberg trajectories to obtain composite maps of mean iceberg concentration, size (thickness), age (day-of-year), and local SST, per 1° grid squares. Selecting icebergs drifting southward across 48°N, per month, we obtain data directly comparable to a key observed index, I48N.
Monthly simulated I48N counts (see Figs. 10, 11, 13) help to explain variable timing of the observed I48N peak, between late spring and early summer (see Fig. 3a). An early summer peak in iceberg numbers is favoured by: (a) “off-shelf” location of the iceberg flux; (b) a later (February) peak influx (perhaps favoured by late retreat of sea ice); (c) lower SST. A summary of observed and simulated annual I48N counts is provided in Table 3. We were not able to simulate enough years for statistical testing, such as with root-mean-square errors for monthly I48N counts (relative to observations), per experimental setup. At a nominal level, best agreement with annual I48N counts in the 2 years of extensive iceberg drift (2014, 2015) is obtained with prescribed February iceberg influx located in the central Labrador Current, and with ocean and atmospheric conditions appropriate to each year (see Table 3).
On the basis of our experiments, we further find that Greenland discharge and environmental conditions appear to influence the I48N counts in a rough ratio of 2:1—i.e. around 1/3 of variation in the I48N count is explained by interannual variations in ocean and atmosphere conditions more or less conducive to iceberg survival to 48°N, with the remaining 2/3 of I48N variation attributed to variation in discharge. This initial finding also demands further scrutiny via rigorous statistical analysis of simulations and observations spanning more years. Further evaluation of modelled size distributions with IIP size observations is potentially informative. However, the reported size data are likely to be less certain than the basic position data, which we currently use. It would also be difficult to relate observed sizes to our input iceberg flux, as we represent size in a statistical sense rather than tracking specific icebergs.
With IIP data available intermittently from 1998, and more reliably from 2009, it would be possible to evaluate further simulations for years prior to 2013, forced with lower frequency (5-daily) data from ORCA025 hindcasts. The current study nevertheless stands as a first-stage proof-of-concept for seasonal iceberg forecasting. To make an actual prediction using the extant SAS-ICB system, we would need the three NARMAX input variables for the preceding months (NAO-index, Greenland surface mass balance, mean SST for the Labrador Sea) to determine the upstream iceberg flux, and a skilful seasonal forecast of winds, surface currents and SST (available via e.g. the GloSea5 system of the Met Office) up to summer of the forecast year. In this study, we used default values for ICB parameters, such as the six drag coefficients and key melt parameters, as in Martin and Adcroft (2010) and Marsh et al. (2015). Varying these parameters across plausible ranges, a “perturbed physics” ensemble of predictions could be obtained, to account for parameter uncertainty, with the forecast obtained as an ensemble mean.
Beyond accounting for parameter uncertainty, there is scope to improve ICB structurally. We currently use surface ocean fields in iceberg momentum and mass balance equations. Vertical shear in ocean currents and temperature stratification may substantially alter both the dynamics and melting rates of icebergs in baroclinic and stratified environments. This is most evident in fjords (FitzMaurice et al. 2016), for which a new parameterisation has recently been proposed (FitzMaurice et al. 2017). However, in the current study, we largely address advection and melting of icebergs in the strongly barotropic (low shear) Labrador Current, where temperature stratification is limited. For these reasons, use of sheared currents and upper ocean temperature profiles is unlikely to substantially alter our findings, although ongoing model development should soon permit iceberg forecasts that account for the effects of shear and stratification on iceberg dynamics and melting.
A further process that may improve forecast skill is the interaction of icebergs with sea ice. Where sea ice concentrations are high (> 90%), observations indicate that icebergs drift predominantly with the pack ice (e.g. Morison and Goldberg 2012). However, in our region of interest, icebergs drift in the open ocean, the marginal ice zone, and together with pack ice that is advecting southward under the influence of ocean currents and prevailing winds (Prinsenberg and Peterson 1992), so the absence of iceberg interaction with sea ice is unlikely to substantially alter our main findings. Finally, we note that the subpolar circulation, and the Labrador Current in particular, is more realistic at a higher resolution of 1/12° (Marzocchi et al. 2015), which is not currently available in the forecast system on which we are trialling seasonal iceberg forecasting. Future improved forecasts will likely be undertaken at this higher resolution.
In conclusion, we emphasize the primary importance of appropriately initializing iceberg distribution/influx and the secondary influence of SST, winds and currents on iceberg drift and melting. Further progress may be achieved with accurate specification of iceberg production at source. This would require appropriate representation of the important process of iceberg melting in transit through Greenland fjords (FitzMaurice et al. 2016; Enderlin et al. 2016), demanding a higher level of model fidelity that we have yet to fully develop. Ancillary investigations with NARMAX reveal dominant lag times of around 6–10 months for icebergs calved from Greenland to reach 48°N. Given accurate knowledge of the iceberg calving around Greenland during autumn and early winter, we envisage that useful seasonal forecasts may be issued for spring/summer iceberg conditions in the northwest Atlantic. Such forecasts should be obtained in coupled mode (Scaife et al. 2014) with the fully interactive NEMO-ICB ocean configuration, as our preliminary analysis suggests that icebergs act to cool and stratify the northwest Atlantic in late spring, favouring persistence of icebergs in the region.
References
Bigg GR (2016) Icebergs: their science and links to global change. Cambridge University Press, Cambridge
Bigg GR, Wadley MR, Stevens DP, Johnson JA (1997) Modelling the dynamics and thermodynamics of icebergs. Cold Regions Sci Technol 26:113–135
Bigg GR, Wei HL, Wilton DJ, Zhao Y, Billings SA, Hanna E, Kadirkamanathan V (2014) A century of variation in the dependence of Greenland iceberg calving on ice sheet surface mass balance and regional climate change. Proc R Soc A. https://doi.org/10.1098/rspa.2013.0662
Blockley EW, Martin MJ, McLaren AJ, Ryan AG, Waters J, Lea DJ, Mirouze I, Peterson KA, Sellar A, Storkey D (2014) Recent development of the Met Office operational ocean forecasting system: an overview and assessment of the new Global FOAM forecasts. Geosci Model Dev 7:2613–2638. https://doi.org/10.5194/gmd-7-2613-2014
Duchez A, Frajka-Williams E, Josey SA, Evans D, Grist JP, Marsh R, McCarthy GD, Sinha B, Berry DI, Hirschi Joel J-M (2016) Drivers of exceptionally cold North Atlantic Ocean temperatures and their link to the 2015 European heat wave. Environ Res Lett. https://doi.org/10.1088/1748-9326/11/7/074004
Dussin R, Barnier B, Brodeau L (2016) The making of the Drakkar Forcing Set DFS5. Drakkar/MyOcean report 01-04-16, LGGE, Grenoble, France
Enderlin EM, Hamilton GS, Straneo F, Sutherland DA (2016) Iceberg meltwater fluxes dominate the fresh-water budget in Greenland’s iceberg-congested glacial fjords. Geophys Res Lett. https://doi.org/10.1002/2016GL070718
FitzMaurice A, Straneo F, Cenedese C, Andres M (2016) Effect of a sheared flow on iceberg motion and melting. Geophys Res Lett. https://doi.org/10.1002/2016GL071602
FitzMaurice A, Cenedese C, Straneo F (2017) Nonlinear response of iceberg side melting to ocean currents. Geophys Res Lett. https://doi.org/10.1002/2017GL073585
Grist JP, Josey SA, Jacobs ZL, Marsh R, Sinha B, Van Sebille E (2016) Extreme air–sea interaction over the North Atlantic subpolar gyre during the winter of 2013–2014 and its sub-surface legacy. Clim Dyn. https://doi.org/10.1007/s00382-015-2819-3
Hill BT (2006) Ship collisions with iceberg database. In: 7th international conference and exhibition on performance of ships and structures in ice, 16–19 July 2006, Banff, Alberta
MacLachlan C, Arribas A, Peterson KA, Maidens A, Fereday D, Scaife AA, Gordon M, Vellinga M, Williams A, Comer RE, Camp J, Xavier P, Madec G (2015) Global Seasonal forecast system version 5 (GloSea5): a high-resolution seasonal forecast system. Q J R Meteorol Soc 141:1072–1084. https://doi.org/10.1002/qj.2396
Madec G (2008) “NEMO ocean engine”. Note du Pole de modélisation, Institut Pierre-Simon Laplace (IPSL), France, No 27 ISSN No 1288-1619
Marsh R, Ivchenko VO, Skliris N, Alderson S, Bigg GR, Madec G, Blaker AT, Aksenov Y, Sinha B, Coward AC, Le Sommer J, Merino N, Zalesny VB (2015) NEMO–ICB (v1.0): interactive icebergs in the NEMO ocean model globally configured at eddy-permitting resolution. Geosci Model Dev 8:1547–1562. https://doi.org/10.5194/gmd-8-1547-2015
Martin T, Adcroft A (2010) Parameterizing the fresh-water flux from land ice to ocean with interactive icebergs in a coupled climate model. Ocean Model 34:111–124
Marzocchi A, Hirschi JJ-M, Holliday NP, Cunningham SA, Blaker AT, Coward AC (2015) The North Atlantic subpolar circulation in an eddy-resolving global ocean model. J Mar Sys 142:126–143. https://doi.org/10.1016/j.jmarsys.2014.10.007
Morison J, Goldberg D (2012) A brief study of the force balance between a small iceberg, the ocean, sea ice, and atmosphere in the Weddell Sea. Cold Reg Sci Technol 76:69–76
Murphy DL, Cass JL (2012) The International Ice Patrol—safeguarding life and property at sea. Coast Guard Proc Mar Safety Security Council 69:13–16
Prinsenberg S, Peterson I (1992) Sea–ice properties off Labrador and Newfoundland during Limex-89. Atmos Ocean 30:207–222
Scaife AA et al (2014) Skillful long-range prediction of European and North American winters. Geophys Res Lett 41:2514–2519. https://doi.org/10.1002/2014GL059637
Smith SD (1993) Hindcasting iceberg drift using current profiles and winds. Cold Regions Sci Technol 22:33–45
Wagner TJW, Eisenman I (2017) How climate model biases skew the distribution of iceberg meltwater. Geophys Res Lett. https://doi.org/10.1002/2016GL071645
Wang Z, Brickman D, Greenan BJW, Yashayaev I (2016) An abrupt shift in the Labrador Current System in relation to winter NAO events. J Geophys Res Oceans 121:5338–5349. https://doi.org/10.1002/2016JC011721
Waters J, Lea DJ, Martin MJ, Mirouze I, Weaver A, While J (2015) Implementing a variational data assimilation system in an operational 1/4 degree global ocean model. QJR Meteorol Soc 141:333–349. https://doi.org/10.1002/qj.2388
Zhao Y, Bigg GR, Billings SA, Hanna E, Sole AJ, Wei H, Kadirkamanathan V, Wilton DJ (2016) Inferring the variation of climatic and glaciological contributions to West Greenland iceberg discharge in the Twentieth Century. Cold Reg Sci Technol 121:167–178
Acknowledgements
SAS-ICB was developed as part of the project “Iceberg forecasting—from days to decades (ICECAST)”, funded by a NERC Innovation Grant (No. NE/M007820/1). We are grateful to the US Coast Guard for compiling and archiving IIP iceberg charts. Tom Lees and Jacob Marsh assisted with digitization of the IIP iceberg charts. We acknowledge Philippe Huybrechts for contributing the original runoff model code, which we used in adapted form to update the GrIS SMB monthly time series. We further acknowledge a wide range of helpful comments from two anonymous reviewers.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Marsh, R., Bigg, G., Zhao, Y. et al. Prospects for seasonal forecasting of iceberg distributions in the North Atlantic. Nat Hazards 91, 447–471 (2018). https://doi.org/10.1007/s11069-017-3136-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-017-3136-4