1 Introduction

Due to the advancements in networking and multimedia coding technology, media such as images are commonly stored and shared over the Internet. This makes them vulnerable to be used for malicious purposes. Hence, image security and encryption has become a much researched area to ensure confidentiality and stop un-authorised access to the digital content. Traditional symmetric ciphers such as Advanced Encryption Standard (AES) [7] are designed with good confusion and diffusion properties. However, standard encryption, methods such as AES seem not to be suitable to cipher data like images [15]. Since 1990, chaotic systems have gained a lot of interest in the field of cryptography due to their desirable properties such as high sensitivity to initial conditions, ergodicity and pseudo randomness. Chaotic systems have also demonstrated great potential for information security especially image encryption [1, 6, 10, 12, 14, 20, 22].

More recently, researchers have showed interest in combining neural network and chaos to develop enhanced encryption algorithms [4, 5, 13, 18, 19]. The authors in [13] have trained the neural network with chaos to replace the chaotic generator in the encryption algorithm. In [19], the chaotic map is used as transfer function for each neuron. They then proposed to use this generator in a stream encryption algorithm where the image is considered as a 1-dimensional array and each bit is encrypted using a binary chaotic output. In [5], neural network biases and weights are adjusted using a chaotic sequence, which would make the output of the neural network very random. The output of the neural network is then used to encrypt image using AES. However, this encryption method uses simple operations such as bit XOR which makes the proposed mechanism easy to break. In addition, the encryption time and computation processing in this case is also quite high.

As well as neural networks, DNA-based chaotic image encryption (and decryption) has been proposed in several works [9, 16, 17, 23, 24]. In Liu et al. [16], each pixel is encoded into four nucleotides and then transferred to their base pairs at random times using a chaotic generator. In Zhang et al. [23], chaos is used to disturb the positions and the values of the pixels and DNA encoding using quaternary code rules to encode the pixel values. In Enayatifar et al. [9], chaotic map function and DNA rules are used to determine a DNA mask which is improved by evolutionary algorithm and used for image encryption. In [17], a cryptanalysis system using DNA rules is proposed in order to break a cryptographic system. The authors in [24] studied security aspects of symmetric ciphers using DNA coding.

In this paper, we propose to combine neural network, chaotic systems and complementary DNA rules in one block encryption algorithm for secure image transmission and storage. Neural network and chaotic functions are used to implement a new heterogeneous chaotic pseudo-random sequence generator. The resulting chaotic sequences are then used as inputs for the proposed encryption operations including pixel position permutation, DNA-based pixel bit permutation and substitution.

The structure of this paper is as follows: Section 2 provides background information and reviews some of the related works on image encryption using neural network and DNA rules. Section 3 introduces the proposed chaos and neural network based pseudo-random sequence generator. Section 4 describes the proposed DNA rules based image encryption algorithm. The simulation results and security analysis of the proposed generator and encryption scheme are given in Section 5. Section 6 gives a conclusion of the results and security features of the proposed encryption system.

2 Background and related work

In this section, we briefly introduce the chaotic functions the most often used in the literature and which we have chosen to use in this paper. Later, we describe some of the most recent chaotic encryption algorithms based on neural network and DNA encoding.

2.1 Chaos and chaotic maps

Several chaotic maps have been proposed in the literature. In this section, we briefly introduce three chaotic maps: Logistic map, Piece Wise Linear Chaotic Map (PWLCM), and Logistic-Tent system.

  1. 1)

    Logistic Map is a simple one-dimensional chaotic map and it is described in (1) as follows:

    $$ x_{n + 1}=p \: x_{n} \left( 1 - x_{n} \right) $$
    (1)

    where p is the control parameter in the range [3.58, 4]. xn and xn+ 1 are the outputs/states of the chaotic map at iterations n and n+ 1 and both are in the interval of (0, 1).

  2. 2)

    Piece-Wise Linear Chaotic Map or PWLCM is a map composed of multiple linear segments and it has better balance properties then the Logistic map. It is defined by (2) as follows:

    $$ \begin{array}{ll} x_{n + 1}& =F \left[ x_{n} \right] \\ &= \left\{\begin{array}{ll} x_{n}/p & \text{if } \: 0 \: \leq x_{n}< p \\ \left( x_{n}-p\right)/\left( 0.5-p\right) & \text{if } \: p \: \leq x_{n} < 0.5 \\ F\left[1-x_{n}\right] & \text{if } \: 0.5 \: \leq x_{n} < 1 \end{array}\right. \end{array} $$
    (2)

    where p is the control parameter in the range (0, 0.5). xn and xn+ 1 are the outputs/states of the chaotic map at iterations n and n+ 1 and both are in the interval of (0, 1). In the proposed generator, the control parameter is restricted to (0.2, 0.3) which produces better chaotic properties compared to the whole range.

  3. 3)

    Logistic-Tent System or (LTS) [25], combines the Logistic and Tent (piece-wise linear) maps into one map as described in (3) below:

    $$ \begin{array}{ll} &x_{n + 1} = \\ & \left\{\begin{array}{ll} \left( p x_{n} \left( 1 - x_{n} \right) + \left( 4-p\right)x_{n}/2 \right) \text{mod } 1&\\ \text{if} \: x_{n}<0.5 \\ \left( p\: x_{n} \: \left( 1- x_{n} \right) + \left( 4-p \right) \left( 1-x_{n}\right)/2 \right) \text{mod }1 &\\ \text{if} \: x_{n}<0.5 \end{array}\right. \end{array} $$
    (3)

where p is the control parameter in the range [0, 4] for chaotic behavior, xn and xn+ 1 are the outputs/states of the chaotic map at iterations n and n+ 1 and both are in the interval of (0, 1).

2.2 Neural network based encryption

In Singla et al. [19], a neural network based chaotic generator is proposed. The neural network parameters such as weights, biases and control parameters were initialized by a 1-D Cubic chaotic map. The neurons of the neural network are assigned PWLCM as their transfer function. The neural network takes 64-bits (eight 8-bit inputs) as the key for the first cycle of its operation and generates a single bit of the pseudo-random sequence on every cycle. After every cycle of the network, the control parameter of each layer is updated by the output of the same layer in order to keep the control parameters close to 0.5 (for best chaotic behavior). The generated sequence had good randomness properties as demonstrated by the tests. The encryption process is implemented by XORing the generated sequence with the image bitstream. There is a shortcoming of the proposed generator here that it produces just a single bit at the output layer after a complete neural network cycle with four layers. We believe it can be improved to reduce computation overhead. Also, the encryption method used is just to XOR the chaotic bits with the image pixel bits which is not very secure.

Kassem et al. [13] use artificial neural networks as a source of perturbation for their proposed generator. The neural network scheme is first trained with PWLCM datasets. Then, it is used to replace the PWLCM function to generate the pseudo random inputs to the system periodically. The proposed neural network perturbation approach enlarges the key space by means of the structure of the neural network (number of layers, activation functions, weights, biases). Adding perturbation increases the cycle’s length and thus avoids the problem of dynamical degradation of the chaotic orbit.

2.3 DNA based encryption

In Awad et al. [2], pixel bit substitution method based on DNA complementary rule is proposed. Authors use DNA complementary rules to calculate new values for the image pixels. Initially, the pixel value is decomposed into four “2-bits” values, and to each of them is assigned a DNA letter (A, T, C and G). Then, DNA letters are converted into binary values using a binary coding rule e.g. A = 00, T = 01 etc. Then, to every letter, a complement is assigned and denoted by C(X) e.g. C(A) = T, C(T) = C etc. A DNA transformation rule is applied on these letters for a number of iterations which, in its turn, calculated using the chaotic generator. The six allowed complementary transformations are shown below,

$$\begin{array}{@{}rcl@{}} Rule_{0}: (AT)(TC)(CG)(GA)\\ Rule_{1}: (AT)(TG)(GC)(CA)\\ Rule_{2}: (AC)(CT)(TG)(GA)\\ Rule_{3}: (AC)(CG)(GT)(TA)\\ Rule_{4}: (AG)(GT)(TC)(CA)\\ Rule_{5}: (AG)(GC)(CT)(TA) \\ \end{array} $$

Out of 8 bit chaotic output, the first 3 bits of the chaotic value are used to select the complementary transformation rule. Of the remaining 5 bits, the 4th and 5th are used to compute the number of iterations of the selected rule for the first DNA letter of the selected pixel block using equation as below:

$$ it\left( 1\right)=mod\left( Ch/2^{3},4\right) $$
(4)

where it is the no. of iterations and ch is the chaotic value. Similarly, 5th and 6th bits are used for the second DNA letter and so on. The transformation works by changing a DNA letter to its complement for each iteration: for example A becomes T after one iteration, then T becomes C for the second iteration and so on. After the iterations of the selected rule on each DNA letter, the resultant DNA letter is then converted into its binary format and substituted in place of the old bits. This process is applied for every pixel of the image to get substituted image.

In Zhang et al. [23], DNA rules based encoding is used to scramble the image pixel values. The image is mapped to a quaternary sequence and a randomly generated key selects the DNA encoding rule. Then, a DNA matrix of size (M, 4xN) is generated, where M xN is the size of the image. A chaotic map is used to generate a chaotic sequence C of length M xN x4 and is transformed to a matrix of size (M, 4xN). Then, for a DNA value, at position (i, j), in the DNA matrix, following rules are applied:

  • if C(i, j)= 0, then no change is done to the value

  • if C(i, j)= 1, then DNA complement is performed and XOR is done

  • if C(i, j)= 2 then DNA value is complemented

  • if C(i, j)= 3 then DNA complement is performed and NXOR (Not Exclusive-Or) is done.

After performing this operation, the new DNA sequence matrix obtained is the encrypted image.

Though these two encryption schemes make use of chaos for encryption, they do not use neural network for generating chaotic sequences which will provide much better performance due to its architecture having several parameters (weights, biases etc). Hence, we propose an encryption scheme which combines chaos generation using neural network and DNA encoding for encryption. In the next section, we present our proposed neural network and chaos based pseudo-random sequence generator.

3 Proposed generator

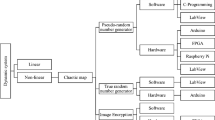
In this section, we present our proposed neural network based chaotic pseudo-random generator. As mentioned earlier, a neural network architecture is used for the generator implementation. Our proposed generator architecture is heterogeneous i.e. more than one chaotic map is used. Figure 1 depicts the proposed generator.

Fig. 1
figure 1

Proposed neural network generator architecture

Full size image

The proposed neural network generator contains four layers: one input layer, two hidden layers and an output layer. Each neuron of the neural network generator uses a chaotic map equation as its transfer function. In the proposed architecture, the input layer has a single neuron and receives a part of the 64-bit encryption key. The key is divided into two 32-bit parts: the first part is used as input for the first cycle of the neural network operation and the second part is used to initialize the neural network parameters. The two hidden layers contain nhl neurons while the output layer contains mol number of neurons (depending on the number of operations to be performed).

A heterogeneous chaotic system is implemented by using different chaotic maps, as transfer functions, alternately in the neural network layers. For example, if the first layer is using Logistic map, then the second layer will have PWLCM and so on. The weight matrices of the four layers, i.e. 0 to 3, (see Fig. 1) are W0,W1,W2, and W3, and are of the sizes 1x1, nhlx1, nhlxnhl, and molxnhl respectively. The bias matrix of the layers are B0,B1,B2, and B3. The control parameter matrix of the chaotic map transfer function are P0,P1,P2, and P3. Both B0-B3 and P0-P3 are of the sizes 1x1, nhlx1, nhlx1 and molx1 in order. The ‘mol’ outputs of the neural network generator can be used for the different operations of the encryption algorithm.

To initialize the neural network generator (weight, bias, control parameter matrices and number of iterations for the first neural network cycle), a 1-D Cubic map is used. The second 32-bit part of the 64-bit key is used as the initial condition for the Cubic map described in (5) below:

$$ x_{n + 1} = \lambda \: x_{n} \left( 1- {x_{n}^{2}} \right) $$
(5)

where xn is the initial condition for the first cycle or the previous state for further cycles of the chaotic function, xn+ 1 is the current state of the chaotic function. Both xn and xn+ 1 are in the range of (0, 1). λ is the control parameter of the chaotic function with a value of 2.59. The map is run initially for 50 iterations in order for the chaotic nature to emerge. Thereafter, its outputs are used to initialize the neural network parameters.

In our paper, we use four outputs, i.e. mol= 4 and then four chaotic sequences are generated:

  • OP4w - is used for pixel position permutation (PPP)

  • OP4x - is used for pixel bit permutation (PBP)

  • OP4y - is used for pixel bit substitution (PBS)

  • OP4z - is used for updating the number of iterations of the chaotic transfer functions of all the neurons

Figure 2 shows the outputs of the output layer (OP4w,OP4x,OP4y, and OP4w) assigned to the operations (PPP, PBS, PBP and updating the number of iterations) respectively. All the outputs of the output layer are XORed and the obtained value is fed back as input after each cycle of the neural network operation. The control parameter of the chaotic map, i.e. transfer function, of each neuron is updated after every cycle of the neural network using the output of the same neuron. To do so, the output of each neuron of every layer is transformed to the range of the control parameter of the chaotic map used for the neuron using (6) as follows:

$$ P_{new}=startingValue+\left( range \times OP\right) $$
(6)

Where startingValue is the value from which the control parameter range begins, range is the difference between the lowest and the highest values of the control parameter and OP is the output of the neuron. For example, for a neuron using the Logistic map, startingValue is 3.58 and range is (4 - 3.58) = 0.42. The transformed output is used to replace the old control parameter of the neuron and the new value will be used in the next cycle of the neural network.

Fig. 2
figure 2

Execution of the proposed generator

Full size image

Subsequently, in this paper, the outputs of the generator are named as per operation that is performed using them, such as PPP sequence for operation pixel position permutation etc. as has been shown in Fig. 2.

4 Proposed image encryption algorithm

In this section, we describe our proposed image encryption algorithm and a new DNA rules based pixel bit permutation algorithm. Figure 3 shows the architecture of the proposed image encryption algorithm. As it can be seen, the outputs from the generator are being used for different operations of the encryption algorithm.

The encryption operation can be divided into two distinct blocks. The first block is the pixel position permutation (PPP-box) block which performs the diffusion of the image pixels, and the second block is the substitution and permutation block, or the SP-box, which is performed at pixel bit level and performs the confusion and diffusion operations.

Fig. 3
figure 3

Proposed encryption algorithm

Full size image

4.1 Pixel position permutation

In the PPP-box, pixel positions in the image are shuffled by identifying the initial position and the target pixel positions in the image. The output PPP from the generator is used to calculate the initial and target positions.

For an N*N image, the first N bits of the PPP sequence is used to calculate the initial position of the random pixel to be permuted. The last N bits are used to calculate the target position for the selected pixel. This process is repeated N*N number of times ensuring that all the pixels’ positions are permuted. If a pixel in initial position is already permuted or a target position is already filled, the nearest available position is selected. Figure 4 depicts the PPP operation where a value in the PPP sequence is used to shift a pixel in position 3 to position N-1.

Fig. 4
figure 4

Pixel position permutation operation of the proposed encryption algorithm

Full size image

4.2 SP-box operation

Input to the SP-box is the pixel position permuted image obtained after the PPP-box. The SP-box contains two separate operations which are performed on per pixel basis of the input image, first chaotic output of PBS and PBP is used for pixel 1, second output PBS and PBP for pixel 2, and so on. First, the chosen image pixel is subjected to the pixel bit substitution operation. Then, the bit substituted pixel undergoes bit permutation operation. In the pixel bit substitution and pixel bit permutation operations, the 32 bits of the chaotic outputs PBS and PBP respectively are used by divided into four bytes as follows:

$$Ch=\left\{Ch1,Ch2,Ch3,Ch4 \right\} $$

and each part is used for the four iterations, i.e. i= 1 to 4, of the SP-box operation for the said pixel.

For bit substitution, we use the DNA based method from [2] that was described earlier in the paper in Section 2. Let us assume that i= 4, hence we are using Ch4 and the let the output pixel be PPBS after bit substitution. The PPBS will be used as the input for the proposed pixel bit permutation operation that is described in the next subsection.

4.3 Proposed DNA-based pixel bit permutation

In this section, we propose a new bit permutation algorithm based on complementary DNA rules. In the bit permutation operation, we permute the bit positions of each pixel. As explained earlier, SP-box operation is iterated four times. For each of the four iterations of the SP-box, one of the four bytes Chi=Ch1,...,Ch4, where i = (1, 4), of the 32-bit PBP value is used.

Since we are considering 4th iteration, i.e., i= 4, of the SP-box, the input is PPBS. We start by considering an array Arr whose values represent the positions of each bit of PPBS bit substituted pixel. Arr can be represented as:

$$Arr=\left[0,1,2,3,4,5,6,7\right] $$

After applying DNA-based bit permutation operation, we get a new permuted pixel PPBP. In subsection below, we explain proposed DNA-based pixel bit permutation.

4.3.1 Pixel bit permutation operation

Within an iteration i of SP-box, bit permutation operation is repeated four times, which we represent by t where t = 1 to 4. We represent the 8 bits of the chaotic output as,

$$Chi=\{Chi_{b0}, Chi_{b1},..Chi_{b7}\} $$

During the ith iteration of the SP-box, for the tth repetition of the permutation operation, the byte Chi is decomposed as follows: the first three chaotic bits {Chib((t− 1)mod8),Chib(tmod8),Chib((t+ 1)mod8)} are used to find the initial selected position and is identified as value V in the array Arr. The bits in V are then used to get the DNA letters on what the DNA transformation rules are applied. The following three bits {Chib((t+ 2)mod8),Chib((t+ 3)mod8),Chib((t+ 4)mod8)} are used to choose the Ruler, i.e. the DNA rule number to apply. The last two bits {Chib((t+ 5)mod8),Chib((t+ 6)mod8)} are used to determine the number of times nrule the DNA rule Ruler is applied.

We are considering i= 4 and let us say t= 1 and Chi={0,1,0,1,0,1,0,1} as shown in Fig. 5. Then, we have V={1,1,0}= 2, Ruler={1,0,0}= 5, and nrule={0,1}= 1(+ 1)= 2. We start by assigning part of Chi, i.e. w={Chib((t− 1)mod8),Chib(tmod8),Chib((t+ 1)mod8)}. We take last two bits of W, i.e. {1,0}, and convert it into a DNA letter, i.e C. Then, we apply the DNA Rule4, which gives new DNA letter A [2]. Then, we convert the new DNA letter A to binary format (which gives us {0,0}) and substituted to last two bits of W which gives new W={1,0,0}. For the next iteration of nrule, we choose first two bits of W, i.e. {1,0}, which gives us C and applying the DNA Rule4 gives new letter A. The new DNA letter is converted to binary, i.e. {0,0}, and substituted at first two bits of W, we get new W={0,0,0}. In the example nrule is 2, hence we stop at this point and the new value we of W is assigned as X. In the example V is 6 and X is 0. We then swap bit at V with bit at X in the array Arr to get Arr’.

$$Arr^{\prime}=\left[6,1,2,3,4,5,0,7\right] $$

We continue this process alternately selecting bits of W for nrule number of times. For next repetition, i.e. t= 2, by assigning t= 2, we get V={1,0,1}= 5, Ruler={0,0,0} = Rule0, and nrule= 2(+ 1)= 3. Following the method, we get X={0,1,1}= 3. By performing permutation of V and X, we get Arr”,

$$Arr^{\prime\prime}=\left[6,1,2,5,4,3,0,7\right] $$

The operation described above is repeated till t = 4. At this point, we have Arr””=[6,1,2,5,4,3,0,7]. The final bit permuted pixel PPBP by shuffling bits to positions of PPBS as indicated by Arr””.

Fig. 5
figure 5

Pixel bit permutation operation of the proposed encryption algorithm

Full size image

5 Image decryption

For decryption of the encrypted image, the same 64-bit key, initially used for encryption, must be used. Decryption follows the reverse process of that of encryption, i.e. the encrypted image first undergoes SP-box and then the pixel position permutation is applied. In the SP-box also the pixel bit permutation operation must be performed prior to the pixel bit substitution operation. This is depicted in the Fig. 6 where the same key is used for the neural network generator parameter initialization and for generating chaotic sequence.

As seen in Fig. 6, the SP-box operation is first. Similar to encryption, we divide the 32-bit chaotic outputs into four 8-bit values. The difference in decryption is that, we reverse order of chaotic sequence for each iteration of SP-box, i.e. i=(4, 1). It is as shown below,

$$Ch=\left\{Ch4,Ch3,Ch2,Ch1 \right\} $$

Let us consider that we are have PPBP and for decryption, we should have Chi={0,1,0,1,0,1,0,1}. Similar to encryption, bit permutation in decryption works by assuming an array as,

$$Arr_{decr}=\left[0,1,2,3,4,5,6,7\right] $$

After 4 repetitions of bit permutation, we get the array Arrdecr=[6,1,2,5,4,3,0,7] which is same as Arr””. Therefore, by swapping bits of PPBP to positions indicated by Arrdecr, we get PPBS. The pixel PPBS then undergoes decryption in bit substitution. Please refer [2] for decryption technique for pixel bit substitution. Again, similar to encryption, SP-box is repeated for four iterations.

The output from SP-box after four iterations is the original image pixel. After SP-box is applied to all the pixels, we obtain the actual values of all the pixels, but their positions are still permuted. Applying PPP-box in reverse will give us the original image with each pixel in their proper position. For PPP-box, the initial and target positions in the permutation operations are reversed, i.e. for an N*N image the first N bits are used to determine the target pixel position and the last N bits are used to find the initial position of the pixel.

Fig. 6
figure 6

Proposed decryption algorithm

Full size image

6 Simulation results and security analysis

Experimental results are given in this section to demonstrate the efficiency of our proposed generator and encryption algorithm. The implementation was developed on Matlab 2012a running on Windows 7 machine with Intel Core i7-3770 3GHz processor and 12GB of RAM.

6.1 Testing the proposed generator

Our proposed generator was tested with several combinations of the chaotic maps that are most used in the literature, such as PWLCM, Logistic, LTS [25] etc. The effect of the number of neurons in the hidden layers and the number of iterations of the chaotic maps are also tested in order to choose the best parameters for the neural network generator.

6.1.1 Choosing generator parameters

To test the randomness properties of the generator with different chaotic map combinations, we have used NIST (National Institute of Standards and Technology) statistical tests [3]. NIST test suite is a statistical package that was developed to test the randomness of arbitrary long binary sequences produced by either hardware or software based cryptographic random or pseudo-random number generators. The test suite consists of 188 statistical tests for evaluating randomness. These tests focus on identifying a variety of different types of non-randomness that could exist in a binary sequence. NIST suite determines if there is any non-randomness or periodicity in the sequence being tested, and decides if the sequence has good enough randomness.

NIST tests were applied on sequences generated from 100 different keys each of length 106 bits. Note that to generate a sequence of length 106 bits, the generator took approximately 661.35 secs.

Table 1 shows the number of failed tests (out of a total of 13 tests) for a common set of keys for several map combinations. It can be seen from Table 1 that, Logistic and PWLCM maps combination passes all the tests. This showed that the approach of using heterogeneous chaotic generator gives the best randomness.

Table 1 Number of Failed Tests in NIST Test Suite Using Different Chaotic Map Combinations With 8 Neurons in the Hidden Layers
Full size table

Table 2 shows the effect of the number of neurons in the hidden layers on the randomness of the generated chaotic outputs when Logistic and PWLCM are used. As we can see, increasing the number of neurons gives better randomness and the generator having 8 neurons passes all the tests.

Table 2 Number of Failed Tests of NIST Test Suite using different No. of neurons in the Hidden layers of the chaotic generator
Full size table

Table 3 shows the effect of number of iterations of the chaotic maps in the neural network on the NIST results, for a fixed combination (Logistic + PWLCM) and the number of hidden layers (8 neurons).

Table 3 Number of failed tests of NIST test suite using different No. of iterations for the chaotic maps in the generator
Full size table

As can be seen the randomness increases when the number of iterations increases and the generator passes all the tests when five iterations were used.

Based on the above results of NIST tests using different parameters for the generator, we chose to use Logistic and PWLCM combination, with 8 neurons in the hidden layers and 5 iterations of the chaotic maps.

6.1.2 NIST test for the chosen generator

The results of NIST test for the three chaotic outputs of the generator (PPP, PBS, PBP), with the above chosen parameters, for hundred different sequences each of length 106 bits are shown in the Table 4.

Table 4 NIST Test Results for 100 Sequences of Length 106 Bits with 100 Different Keys
Full size table

It can be seen from Table 4 that all the 3 sequences passed all the tests of NIST test suite. It also means that 3 different sequences can be generated simultaneously for different encryption operations.

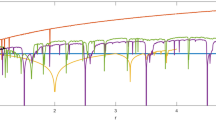
Figure 7 shows the chaotic signal for the first output PPP of our proposed generator.

Fig. 7
figure 7

State sequence of the proposed generator for one of the sequences

Full size image

6.1.3 Autocorrelation

The autocorrelation test performed on the generated sequence PPP is shown in Fig. 8. As we can see, the sequence does not contain any periodicity and produces similar result of a random signal with zero value for non-zero time shift.

Fig. 8
figure 8

Autocorrelation function of the generated chaotic sequence PPP

Full size image

6.1.4 0/1 balance test

The 0/1 balance property is the ratio of the number of bits with a value ‘0’ to that of number of bits with value ‘1’. A value of 50 for this property means, good randomness, i.e. the sequence has equal number of “0s” and “1s”.

For this test, we calculated the 0/1 balance for hundred sequences (each of length 106 bits) using different keys. The average values for the three chaotic outputs of our generator are shown in Table 5.

Table 5 Comparison of 0/1 Balance
Full size table

Table 5 shows that the generated sequences have good 0/1 balance properties comparing to the results obtained in [13] and [19]. Note that the best results obtained, for the 100 sequences tested, are 50, 50.001 and 50 for the three sequences PPP, PBS and PBP.

6.1.5 Attractor test

Phase space is the plot of a system’s previous state to its new state. It is also called attractor for the reason that the plot shows if the system is being attracted to a steady state. It can indicate randomness in a system if the system does not seem to have a steady state region. Figure 9 shows the 2D phase space plot for the proposed generator. From the plot, it can be seen that there is no steady state region in the plot, which signifies that the signal generated is highly random and chaotic. It also shows that the system has an inherent perturbation mechanism due to neural network architecture and dynamic control parameter variation which prevents the system from going into a steady state.

Fig. 9
figure 9

2D phase space plot of the proposed generator

Full size image

6.1.6 Histogram analysis

The histogram of the generated sequence is shown in Fig. 10. As we can see, the chaotic values in the range of (0, 1) are distributed equally, which means that the generated sequence is highly random.

Fig. 10
figure 10

Histogram plot of the proposed generator

Full size image

6.1.7 Key sensitivity test

In this test, two different keys with just 1-bit difference were used to generate two sequences using our proposed generator. We have used PPP sequence to perform this test but similar results were obtained for PBS and PBP. In order to compare them, their cross-correlation is plotted as shown in Fig. 11.

Fig. 11
figure 11

Cross correlation of 2 PPP sequences with 1-bit change in the initial key

Full size image

As it can be seen, the two sequences are entirely different which proves the sensitivity of the generator to the secret key and initial conditions. Similar cross correlation figures were obtained for the other two sequences PBS and PBP.

Figure 12 shows the cross correlation plot between PBP and PBS sequences.

Fig. 12
figure 12

Cross correlation between multiple generated sequences at the same time

Full size image

As it can be seen, there is no similarity between the generated chaotic sequences from different neurons in the output layer of the generator.

6.2 Testing the proposed encryption algorithm

We applied our encryption algorithm on several test images of various sizes such as Lena and Mandrill of sizes 256*256 and 512*512 for both gray-scale and RGB colour images. In this section, several tests were performed to measure the randomness of the encrypted images and resilience of the algorithm against attacks and the results are compared to a number of existing encryption algorithms. The encryption time for a 256*256 Lena image is approximately 74 secs.

6.2.1 Histogram analysis

The histogram of an image shows the distribution of the pixel intensity values in the range of (0, 256). If the intensity of the pixels are uniformly distributed, then the image is highly random and highly resistant against statistical attacks.

Figure 13 shows the plain gray-scale Lena image of size 256*256, its corresponding encrypted image and histograms of plain and encrypted Lena images. It can be seen from Fig. 13b and d that the histograms of the plain and encrypted images are very different and that the pixel intensity values are uniformly distributed. The average pixel intensity obtained for 100 encrypted images is 127.4612 which is very close to the ideal value of 127.5 and is better than the result of 127.5689 found in [19]. Note that the best average pixel intensity value obtained for one of the 100 tested encrypted images was 127.5067.

Fig. 13
figure 13

a Plain Lena Image, b Histogram of Plain Lena Image c Encrypted Lena Image, and d Histogram of Encrypted Lena Image

Full size image

6.2.2 Correlation of two adjacent pixels

Adjacent pixels on an average are correlative to an extent of 8 to 16 pixels. Randomness is better if correlation between adjacent pixels is as low as possible. We calculate the correlation coefficients for horizontally, vertically and diagonally adjacent pixels using (7–10):

$$ E\left( x\right)=\frac{1}{M \times N} \sum\limits_{i = 1}^{M} \sum\limits_{j = 1}^{N} P\left( i,j\right) $$
(7)
$$ D\left( P\right)=\frac{1}{M \times N} \sum\limits_{i = 1}^{M} \sum\limits_{j = 1}^{N} \left[ P\left( i,j\right)-E\left( P\left( i,j\right)\right)\right]^{2} $$
(8)
$$ \begin{array}{lll} Cov\left( P,C\right)= \frac{1}{M \times N} {\sum}_{i = 1}^{M} {\sum}_{j = 1}^{N} \left[ P \left( i,j \right)- E \left( P \left( i,j \right) \right) \right] \\ \left[C\left( i,j\right) -E \left( P\left( i,j\right)\right) \right] \end{array} $$
(9)
$$ r_{PC}=\frac{Cov(P,C)}{\sqrt{D(P)} \sqrt{D(C)}} $$
(10)

where P(i, j) and C(i, j) are the intensity values of the original and encrypted pixels.

Figure 14a and b show the correlation distribution of horizontally adjacent pixels for plain and encrypted images of Lena.

Fig. 14
figure 14

Horizontal Pixel Correlation of Lena Image a Plain and b encrypted

Full size image

As we can see, a high correlation appears in Fig. 14a. However, this correlation is suppressed in the encrypted image where the values of adjacent pixels are quite different.

The correlation coefficients calculated for the original and encrypted images are shown in Table 6 for a number of grayscale images and in Table 7 for coloured images. In addition, a comparison is given with existing encryption algorithms.

Table 6 Adjacent Pixel Correlation for Grayscale plain and encrypted images
Full size table
Table 7 Adjacent Pixel Correlation for Color Plain and Encrypted Images
Full size table

Tables 6 and 7 show that the values of the correlation coefficients are very close to ‘0’, which proves that encrypted image is very random. As it can be seen, the obtained correlation values are better than [2, 19] and [23] at least in two of the three dimensions. Also compared to other works described earlier such as [13, 16] and [9], we get better results in all the dimensions.

6.2.3 Information entropy

Information entropy is a statistical tool to measure the randomness present in an image and characterizes the texture of the image. Entropy H(m) of a message source m is given by the (11),

$$ H\left( m\right)=\sum\limits_{i = 0}^{2^{N}-1} p\left( m_{i} \right) \log_{2} \frac{1}{p(m_{i})} $$
(11)

where p(mi) is the probability of occurrence of a message symbol mi. A message source m is considered to be random if there are 28 or 256 possible outcomes of the message each of which has equal probability of occurrence. Hence, a value of 8 for the entropy means that the message source is highly random. Table 8 presents the average entropy value obtained for 100 encrypted images with 100 different keys for several test images. The obtained results are compared with existing algorithms.

Table 8 Entropy Values for the Proposed Algorithm With Related Works
Full size table

As we can see, the entropy values are very close to 8 which means that the information leakage is negligible and the encryption system is secure against entropy attack. When comparing the results obtained for our algorithm to similar related works for different images, we can see that our proposed algorithm gives higher entropy than the results shown in [2, 11, 13, 16] and [9] (for Mandrill 512*512 grayscale), similar to [19] and [9] (for Lena 512*512 gray) and it is slightly lower than [23] with a difference of 0.0002. However, the correlation of adjacent pixels are better for our proposed algorithm comparing to [23].

6.2.4 NPCR and UACI

Common measures like NPCR (Number of Pixels Change Rate) and UACI (Unified Average Changing Intensity) are used to test the difference between the original image P and the encrypted one C as given by (12–14):

$$ D\left( i,j\right) = f\left( x\right)= \left\{\begin{array}{ll} 1 & \text{if} \: P\left( i,j \right) \neq C \left( i, j\right) \\ 0 & \text{else} \end{array}\right. $$
(12)
$$ \begin{array}{lll} NPCR=\frac{ {\sum}_{i = 0}^{M-1} {\sum}_{j = 0}^{N-1} D\left( i,j \right)}{M \times N} \times 100 \end{array} $$
(13)
$$ \begin{array}{ll} UACI=\frac{1}{M \times N} {\sum}_{i = 0}^{M-1} {\sum}_{j = 0}^{N-1} \frac{|P(i,j)- C(i,j)|}{255} \times 100 \end{array} $$
(14)

where P(i, j) and C(i, j) are the intensity values of the pixels at the position (i, j) in the plain and encrypted images of size M*N respectively.

Table 9 below shows the NPCR and UACI results for a number of test images encrypted by our proposed algorithm and some of the related works.

Table 9 NPCR and UACI Results for the Proposed Encryption Algorithm and Related Works
Full size table

We compared the NPCR and UACI between the plain image and encrypted grayscale Lena image (of size 256*256) produced by our proposed encryption algorithm and compared with some of the related work. We found that our calculated NPCR is higher than the values found in [2] when the UACI is slightly lower with a difference of 0.0154. The NPCR is slightly lower than [19] with a difference of 0.0045. However, as we mentioned earlier, the adjacent pixels correlation is better with our algorithm and the entropy is similar.

We also calculated the NPCR and UACI for the color image of Mandrill (of size 256*256) as shown in Table 10. Our obtained NPCR was slightly lower than [13] by 0.0576. However, the percentage of adjacent pixels as well as the entropy was better with our algorithm. Furthermore, the obtained NPCR and UACI are high enough to prove that the plain and encrypted image are very different.

6.2.5 Key-sensitivity test

For any encryption algorithm, it is important that a small change in the key produces an entirely different cipher text. In order to test this, we used two keys with just a single bit difference and used them to encrypt the same Lena gray-scale 512*512 image. Figure 15 shows the difference between the two cipher images. It can be seen that the difference is not equal to zero for nearly all the pixels which means that the two encrypted images are entirely different even with just a single bit difference in the keys used to encrypt them.

Fig. 15
figure 15

Difference between 2 encrypted Lena images with 1-bit change in the initial key

Full size image

We calculated the percentage of changed pixels in the two cipher images and we got a value of 99.60%, which indicates that nearly all the pixels are dissimilar, and hence proves that the two encrypted images are completely different [21].

6.2.6 NIST statistical tests

NIST tests were performed on 100 encrypted Lena 512*512 gray-scale images, each encrypted with hundred different keys. Table 10 below shows the obtained results of NIST tests. As it can be observed, all the tests were passed with a minimum passing rate of 98%.

Table 10 NIST Results for 100 Encrypted Lena 512x512 Images
Full size table

6.2.7 Plaintext sensitivity

In this section, we will discuss the sensitivity of our algorithm to the plain image. As it can be observed, the algorithm is shown and tested in the Electronic Codebook (ECB) mode i.e. the encryption and decryption of each block of the image is independent from the other blocks or pixels. Therefore, under a given key, any given plain image block always gets encrypted to the same encrypted image block and then the encryption in this mode is not very sensitive to the original image. If this property is undesirable, then as mentioned in [8], the ECB mode should not be used”. A cryptographic mode of operation usually combines the basic encryption method with some sort of feedback and some simple operations. The most popular confidentiality modes of operation for symmetric key block encryption are the Electronic Codebook (ECB) mode, Cipher Block Chaining (CBC), Cipher Feedback (CFB) mode, Output Feedback (OFB) mode and Counter (CTR) modes. When a block is changed in the plain image (or in the encrypted image) results in a different number of changed number of encrypted blocks (or decrypted blocks) depending on the chosen mode of operation. For example, OFB mode avoids the propagation of errors in the decrypted image, when an error occurs in the encrypted image (a bit is changed). However, its robustness to the chosen plaintext attack and differential attack is not guaranteed. CBC mode doubles the errors in the decrypted image but the algorithm in this mode is more resistant to this type of attack. As it can be concluded, this is relative to the chosen mode of operation and not to the proposed encryption algorithm. Our algorithm is compliant with NIST recommendations exposed in [8] and same results are obtained for the standard AES encryption algorithm.

7 Conclusions

In this paper, a heterogeneous chaotic generator, implemented using neural network, is proposed. The heterogeneity of the generator is obtained by alternating two different chaotic maps; Logistic and PWLCM, in the neural network layers. The proposed generator is highly random and possesses good chaotic properties as shown in the test results including auto-correlation, cross-correlation, 0/1 balance and NIST tests. The 0/1 balance was compared to similar works in pseudo-random generators and it was seen that our proposed generator difference between 50-50 distribution of 0s and 1s was on average 0.004 while similar works achieved at best 0.01. Hence, our proposed generator is nearly 10 orders better on 0/1 balance. The NIST was conducted on 100 sequences, and on average of 100 sequences 99.2 passed the test with lowest being 96. In addition, using our proposed generator, several chaotic sequences can be generated simultaneously by varying the number of neurons in the output layer which allows to perform a number of cryptographic operations with a minimum number of the neural network cycles. In the paper, we also proposed a new encryption algorithm using chaotic generator as input for its cryptographic operations including: pixel position permutation, DNA based substitution and DNA based bit permutation which was also introduced in this paper to enhance the statistical properties of the encrypted images. Several tests were performed on the encrypted images such as correlation, entropy, histogram, NIST statistical test etc. Histogram analysis shows that for 100 encrypted images, we get average value for pixel intensity of 127.46 which is close to ideal value of 127.5. The entropy value for encrypted images is very close to 8, with average difference between entropy of proposed method to 8 being 0.003. The entropy value was compared to other works, and in most cases it is similar or better than similar works. NIST tests one 100 images showed that all the images passed all the tests. From the test and comparisons to similar works, it is proved that the proposed encryption algorithm has high cryptographic quality and it is compliant with NIST standards.