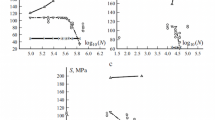
A review of the previous works of the authors dedicated to the use of Daniels’ sequence (DS) for analyzing the relation between the distribution of the static strength of components of a unidirectional fibrous composite (UFC) and the distribution of its fatigue life is presented. A generalization of the DS which can be used to analyze the association of distribution of the static strength of composite components with distribution of the static strength of the UFC itself is given. In analyzing the fatigue life of a UFC, unlike in Daniels’ model, the loading rate and randomness of the number of still workable components in the weak microvolume in which the destruction process takes place are taken into account. By analyzing the fatigue life, it is possible to explain the existence of the random fatigue strength and to calculate the maximum load at which the probability of absence of fatigue failure is great enough when the number of cycles of fatigue loading tends to infinity. Numerical examples of processing of experimental data are presented, and estimates for parameters of the corresponding nonlinear regression model, which can be interpreted as the strength parameters of UFC, are obtained.







Similar content being viewed by others
References
F. T. Peirce, “The weakest link. Theorem on the strength of long and composite specimens,” J. Text. Inst. Trans., 17, No. 7, 355-68 (1926).
H. E. Daniels, “The statistical theory of the strength of bundles of threads,” Proc. Royal Soc. London, Ser. A, No. 183, 405-435 (1945).
R. L. Smith, “The asymptotic distribution of the strength of a series-parallels system with equal load sharing,” Ann. Prob., 10, 137-171 (1982).
D. E. Gucer and J. Gurland, “Comparison of the statistics of two fracture modes,” J. Mech. Phys. Solids, 10, 365-373 (1962).
J. Bogdanoff and F. Kozin, Probabilistic Model of Damage Accumulation [Russian translation], Mir, Moscow (1989).
K. Goda, T. Okabe, and N. Takeda, “A strength reliability model of unidirectional fiber-reinforced ceramic matrix composites by Markov process,” Adv. Comp. Mater., 15, No. 3, 263-285 (2006).
Yu. Paramonov and J. Andersons, “A family of weakest link models for fiber strength distribution,” Composites: Pt A, 38, 1227-1233 (2007).
Yu. Paramonov, “Extended weakest link distribution family and analysis of fiber strength dependence on length,” Composites: Pt A, 39, 950-955 (2008).
Yu. Paramonov and J. Andersons, “Analysis of the fiber length dependence of its strength by using the weakest-link approach. 1. A family of weakest-link distribution functions,” Mech. Compos. Mater., 44, No. 5, 479-486 (2008).
Yu. Paramonov and J. Andersons, “Analysis of the fiber length dependence of its strength by using the weakest-link approach. 2. Analysis of test data,” Mech. Compos. Mater., 45, No. 1, 45-52 (2009).
Yu. Paramonov, J. Andersons, and S. Varickis, “MinMaxDM distribution family for a series of parallel systems with defects and the tensile strength of a composite material,” Int. J. Performability Eng., 8, No. 3, 299-309 (2012).
Yu. Paramonov, M. Kleinhofs, and A. Paramonova, “Markov model of connection between the distribution of static strength and the fatigue life of a fibrous composite,” Mech. Compos. Mater., 42, No. 5, 431-442 (2006).
Yu. M. Paramonov, J. Andersons, M. A. Kleinhofs, and A. Yu. Paramonova, “Markov model for analyzing the residual static strength of a fiber-reinforced composite,” Mech. Compos. Mater., 44, No. 4, 389-396 (2008).
Yu. Paramonov, J. Andersons, M. Kleinhofs, and I. Blumbergs, “MinMaxDM distribution functions for an analysis of the tensile strength of a unidirectional composite,” Mech. Compos. Mater., 46, No. 3, 275-286 (2010).
Yu. Paramonov, R. Chatys, J. Andersons, and M. Kleinhofs, “Markov model of fatigue of a composite material with Poisson process of defect initiation,” Mech. Compos. Mater., 48, No. 2, 217-228 (2012).
Yu. Paramonov, R. Chatys, J. Andersons, V. Cimanis, and M. Kleinhofs, “Markov models for tensile and fatigue reliability analysis of unidirectional fiber composite,” RT&A, 03, No. 26, 53-65 (2012).
Yu. Paramonov, A. Kuznetsov, and M. Kleinhofs, Reliability of Fatigue-Prone Airframes and Composite Materials, Riga Techn. Univ., Riga (2011). (<http://gnedenko-forum.org/library/Paramonov/Reliability_Paramonov.pdf>)
V. Cimanis and Yu. Paramonov, “Fatigue curve approximation using Daniels’ sequence and Markov chains,” Mater. Dig. XXIV Sci. Pract. Conf. Theory and Practice in Physical, Mathematical and Technical Sciences, IASHE, London, 31-33 (2012).
Yu. Paramonov, V. Cimanis, S. Varickii, and M. Kleinhofs, “Investigation of the reliability and longevity of parallel systems with defects using Daniels’ sequences,” Automat. Contr. Comput. Sci., 47, No. 2, 87-93 (2013).
M. Kleinhofs, Investigation of the Static Strength and Fatigue of a Composite Material Used in Aircraft Structures. PhD thesis, Riga (1983).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Mekhanika Kompozitnykh Materialov, Vol. 49, No. 5, pp. 821-838 , September-October, 2013.
Rights and permissions
About this article
Cite this article
Paramonov, Y., Cimanis, V., Varickis, S. et al. Modelling the Strength and Fatigue Life of a Unidirectional Fibrous Composite by Using Daniels’ Sequence and Markov Chains. Mech Compos Mater 49, 551–562 (2013). https://doi.org/10.1007/s11029-013-9371-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11029-013-9371-1