Abstract
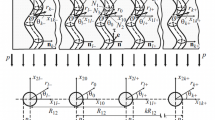
Within the framework of a piecewise homogeneous body model, with the use of three-dimensional geometrically nonlinear exact equations of elasticity theory, a method for determining the stress—strain state in unidirectional fibrous composites with locally curved fibers is developed for the case where the interaction between the fibers is neglected. All the investigations are carried out for an infinite elastic body containing a single locally curved fiber. Numerical results illustrating the effect of geometrical nonlinearity on the distribution of the self-balanced normal and shear stresses acting on the interface and arising as a result of local curving of the fiber are presented.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
Yu. M. Tarnopol’skii, V. I. Zhigun, and V. A. Polyakov, Spatially Reinforced Composite Materials, Handbook [in Russian], Mashinostroenie, Moscow (1987).
A. N. Guz’, Failure Mechanics of Composite Materials in Compression [in Russian], Naukova Dumka, Kiev (1990).
A. Kelly, “Composite materials: impediments to wider use and some suggestions to overcome them,” in: Proceedings of ECCM-8, 3–6 June, Napoles, Italy. Vol. I (1998), pp. 15–18.
S. D. Akbarov and A. N. Guz’, Mechanics of Curved Composites, Kluwer Academic Publ. (2000).
A. N. Guz’, “A two-level model in the mesomechanics of compression fracture of cracked composites,” Int. Appl. Mech., 39, No.3, 274–285 (2003).
S. D. Akbarov and A. N. Guz’, “Method of solving problem in the mechanics of fiber composites with curved structures,” Sov. Appl. Mech., No. 3, 777–785 (March, 1985).
S. D. Akbarov and A. N. Guz’, “Mechanics of curved composites (piecewise homogeneous body model),” Int. Appl. Mech., 38, No.12, 1415–1439 (2002).
R. Kosker and S. D. Akbarov, “Influence of the interaction between two neighboring periodically curved fibers on the stress distribution in a composite material,” Mech. Compos. Mater., 39, No.2, 165–176 (2003).
S. D. Akbarov and R. Kosker, “On a stress analysis for an infinite elastic body with two neighboring curved fibers,” Composites, Pt. B: Eng., 34, No.2, 143–150 (2003).
E. K. Dzhafarova, “Solution method for stress-strain state problems in fibrous composites with locally curved structures,” in: Proceedings of Young Scientists’ Conference, Pt. I [in Russian], Institute of Mechanics of the Ukrainian Academy of Sciences, Kiev (1992), pp. 39–44.
E. K. Dzhafarova, “Distribution of self-equilibrated stresses in fibrous composite materials with local curvings in their structures,” Dep. in VINITI 07.09.94, No. 2166-B94 [in Russian] (1994).
E. K. Dzhafarova, Stress State in Composite Materials with Locally Curved Fibers, Candidate’s Dissertation [in Russian], Institute of Mathematics and Mechanics of the National Academy of Sciences of Azerbaijan, Baku (1995).
A. N. Guz, Fundamentals of the Three-Dimensional Theory of Stability of Deformable Bodies, Springer (1999).
Author information
Authors and Affiliations
Additional information
__________
Russian translation published in Mekhanika Kompozitnykh Materialov, Vol. 41, No. 4, pp. 433–448, July–August, 2005.
Rights and permissions
About this article
Cite this article
Akbarov, S.D., Kosker, R. & Simsek, K. Stress Distribution in an Infinite Elastic Body with a Locally Curved Fiber in a Geometrically Nonlinear Statement. Mech Compos Mater 41, 291–302 (2005). https://doi.org/10.1007/s11029-005-0055-3
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/s11029-005-0055-3