Development of a high-resolution spatial inventory of greenhouse gas emissions for Poland from stationary and mobile sources

Abstract

Greenhouse gas (GHG) inventories at national or provincial levels include the total emissions as well as the emissions for many categories of human activity, but there is a need for spatially explicit GHG emission inventories. Hence, the aim of this research was to outline a methodology for producing a high-resolution spatially explicit emission inventory, demonstrated for Poland. GHG emission sources were classified into point, line, and area types and then combined to calculate the total emissions. We created vector maps of all sources for all categories of economic activity covered by the IPCC guidelines, using official information about companies, the administrative maps, Corine Land Cover, and other available data. We created the algorithms for the disaggregation of these data to the level of elementary objects such as emission sources. The algorithms used depend on the categories of economic activity under investigation. We calculated the emissions of carbon, nitrogen sulfure and other GHG compounds (e.g., CO₂, CH₄, N₂O, SO₂, NMVOC) as well as total emissions in the CO₂-equivalent. Gridded data were only created in the final stage to present the summarized emissions of very diverse sources from all categories. In our approach, information on the administrative assignment of corresponding emission sources is retained, which makes it possible to aggregate the final results to different administrative levels including municipalities, which is not possible using a traditional gridded emission approach. We demonstrate that any grid size can be chosen to match the aim of the spatial inventory, but not less than 100 m in this example, which corresponds to the coarsest resolution of the input datasets. We then considered the uncertainties in the statistical data, the calorific values, and the emission factors, with symmetric and asymmetric (lognormal) distributions. Using the Monte Carlo method, uncertainties, expressed using 95% confidence intervals, were estimated for high point-type emission sources, the provinces, and the subsectors. Such an approach is flexible, provided the data are available, and can be applied to other countries.

Introduction

To counter the impacts of climate change, greenhouse gas (GHG) emissions must be reduced. Reductions can be monitored through inventories of emissions and absorptions of these gases. To that end, the national inventory reports are a useful tool for verifying agreed commitments to reduce or stabilize emissions, to estimate the global carbon budget (Le Quéré et al. 2015), to predict the emissions under different scenarios, and to develop and implement new agreements, see, e.g., Spencer et al. (2016) and Smith et al. (2015). GHG inventories at national or provincial levels include data on emissions for many categories of human activity, and the total emissions are calculated using the global warming potential factors of each GHG. The United Nations Framework Convention on Climate Change (UNFCCC), the International Energy Agency (IEA), and the Carbon Dioxide Information Analysis Center (CDIAC) are examples of bodies that collect national inventory submissions and data on emissions broken down by fossil fuel type and by GHG. However, for a more in-depth study of emission processes as well as their structure, it is more appropriate to use spatially explicit data on GHG emissions. Such data link the emissions to the territory in which they appear (Oda and Maksyutov 2011; Olivier et al. 2005). Thus, they have been used in the past as input data for the simulation of atmospheric CO₂ fluxes in global circulation and transport models (Déqué et al. 2012; Neale et al. 2013; Lamarque et al. 2013). Spatially explicit data are also useful for scientists and policy makers at provincial and local levels to identify the main sources of emissions, their shares in the total emissions, and the composition of emitted GHGs. The compilation of spatial data is an area of considerable interest as evidenced by many recent studies (Andres et al. 2009; Gosh et al. 2010; Gurney et al. 2009; Hutchins et al. 2017; Oda and Maksyutov 2011; Olivier et al. 2005; Pétron et al. 2008; Puliafito et al. 2015; Raupach et al. 2010; Rayner et al. 2010; Denier van der Gon et al. 2017).

Spatial data on GHG emissions are usually presented in the form of a spatial grid, also referred to as gridded emissions. Emission data at the national or provincial level are disaggregated in order to estimate emissions in each grid cell. These disaggregation algorithms need additional proxy data, e.g., population density. Data from remote sensing can also be used as proxy data, e.g., nighttime light intensity, land use data, etc. Since remote sensing does not measure the actual emissions of the sources, algorithms are needed to calculate the emissions in each grid cell: see e.g., Horabik and Nahorski (2014). The final resolution of the gridded emissions is generally determined by the resolution of the proxy data used. Advantages of using remote sensing are the possibility to estimate GHG emissions spatially for large territories (ideally for the whole globe) and the ease of updating emission data over time. These approaches are mainly used for gridded emissions of carbon dioxide (CO₂) as a major GHG produced by humans, which are mainly a result of fossil fuel combustion processes (including emissions by large point sources), land use change, and forestry. But there are many categories of anthropogenic activity where emissions cannot be estimated remotely, e.g. emissions of non-methane volatile organic compounds (NMVOCs) or emissions of sulfur hexafluoride (SF₆), which is an extremely potent greenhouse gas, among many others.

Efforts have been made to increase the spatial resolution of the GHG estimates, since a higher resolution better reflects the specifics of territorial emission processes (Andres et al. 1996; Oda and Maksyutov 2011; Olivier et al. 2005; Rayner et al. 2010). Grid cell sizes have decreased from 1° latitude and longitude for global fossil fuel CO₂ emissions (Andres et al. 2009) to 0.25° (Rayner et al. 2010) and to 1 km for a global fossil fuel CO₂ emission inventory derived using a point source database and satellite observations of nighttime lights as proxy data (Oda and Maksyutov 2011). Spatially explicit GHG emission inventories have also been developed at the regional level, e.g. fossil fuel CO₂ emissions (Maksyutov et al. 2013; Raupach et al. 2010), fossil fuel combustion CO₂ emission fluxes for the USA (Gurney et al. 2009), as well as data of emission sector or category such as power generation (Pétron et al. 2008), North American methane emissions (Turner et al. 2015), or the road transport sector in Argentina (Puliafito et al. 2015).

There are a number of problems in the practical implementation of GHG gridded emission estimates due to the use of diverse grids for the input proxy data with different spatial resolutions. These may also differ from the desired target resolution of the gridded emissions. When combined, the task is to determine which portion of the grid cell in one grid relates to the partly overlapping cell of the target grid (Verstraete 2014). These grids can differ in cell size, they can be displaced in any latitude and longitude direction, and they can even be rotated by a certain angle. To address this overlay problem, approaches based on fuzzy logic and artificial intelligence techniques can be used (Verstraete 2017, 2018). Another problem is that most GHG gridded emission calculations do not fully take into account the state and provincial administrative boundaries, and usually, a cell is assigned to an administrative unit based on where the majority of the area falls.

A common feature of previous studies on the spatial inventory of GHGs at the regional level was that they were primarily based on a grid of a certain size. Furthermore, the sources of emissions of various types were analyzed within the cells of this grid, and the spatial emissions were estimated exclusively for the grid. This caused some difficulties, particularly due to the strong dependence of the results on the grid. For example, its size could not be changed, and there were significant losses of accuracy when aggregating results to the level of small administrative units (such as municipalities). This approach has been used, in addition to the references mentioned previously, in studies reported by Bun et al. (2007), Boychuk et al. (2012), Boychuk and Bun (2014), Valakh et al. (2015), and Halushchak et al. (2016), which are closely related to this study, although they covered only a limited set of emission categories.

In this paper, we propose a completely different approach for estimating a spatially resolved GHG inventory, which is not initially based on a regular grid. Instead, we consider emission processes at the level of emission sources, classified into point-, line-, and area-type sources. Using source-related data, we created a geospatial database with input parameters and calculated the emissions for each category of human activity using activity data and emission coefficients. The activity data at the level of separate emission sources are calculated using some proxy data and algorithms for disaggregation of the data to the source level, which differs depending on the category of human activity. The digital maps of these emission sources retain information about their administrative assignment; therefore, we can analyze emissions spatially at any administrative level up to municipalities, taking into account administrative boundaries, which eliminates the problems associated with traditional gridded emission approaches. In the final stage, the emissions from very diverse point-, line-, and area-type sources can be combined to calculate the total emissions in each grid cell, where the target spatial resolution can be very high, e.g., 100 m. In this study we analyzed all categories of human activity covered by the IPCC Guidelines (IPCC 2006), e.g., the production of lime, glass, sugar, paper, ammonia, nitric acid, etc., which includes more than 100 categories in total, using Poland as a case study. These results include the spatial distribution of not only CO₂, but also other GHGs, as well as the spatial distribution of emissions from different types of fossil fuels. This very detailed spatial inventory is available for all of Poland. In contrast, this would not be possible using remote sensing and a purely gridded emissions approach, which would only provide much more generalized results, e.g., emissions from fossil fuel combustion as a whole.

The implementation of this approach for the development of a GHG spatial inventory for other sectors, in particular for electricity generation and fossil fuel processing (Topylko et al. 2015), the residential sector (Danylo et al. 2015), the industrial sector (Charkovska et al. 2018b), and agriculture (Charkovska et al. 2018a) were presented at the 4th International Workshop of Uncertainty of Atmospheric Emissions.

Methodology and input data

The spatial GHG inventory approach

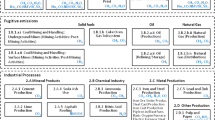
The primary elements of the proposed approach for creating a GHG spatial inventory are presented in Fig. 1. For all sectors and categories of anthropogenic activity covered by the United Nations Intergovernmental Panel on Climate change (IPCC) guidelines (IPCC 2006), the sources of emissions or sinks are analyzed in terms of their specific features and their spatial representation in the inventory. For example, each car is a source of GHG emissions, but it is not realistic to monitor each vehicle. Therefore, we consider a road as the emission source and describe it by certain parameters such as category and intensity. Similarly, for glass production, we can obtain the geographic coordinates of the stacks and treat these as point-type emission sources. In this way, we analyzed all categories of activity in terms of practical implementation within the GHG spatial inventory, classifying them into point, line, and area types depending on their emission intensity and physical size as compared to the territory under investigation (see the Sect. 2.2.1 for more details). We refer to these point-, line-, and area-type sources as “elementary objects” in our GHG spatial inventory.

Fig. 1

Steps in the development of a GHG spatial inventory

Digital maps of emission sources/sinks are then built for each category of human activity. For some categories, they are digital maps of point objects while for other categories they are digital maps of linear objects or area-type objects (see block “Digital maps” in Fig. 1). If needed, the line- and area-type (diffused) elementary objects are split by administrative boundaries. This allows us to allocate each elementary object to the corresponding provinces (voivodeships in Poland), districts (powiats), or municipalities (gminas).

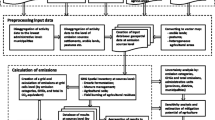
The next step is to calculate GHG emissions from the elementary objects. This reflects the main principles of the IPCC Guidelines (IPCC 2006), i.e., the emission is a product of the activity data and the corresponding emission factors (see block “Mathematical models of emissions” in Fig. 1). However, a common problem is to obtain data about the activities at the level of the elementary objects. For this purpose, we have developed algorithms for disaggregation of the available statistical data for provinces (or even for municipalities in some categories) to the level of elementary objects (see block “Data disaggregation algorithms” in Fig. 1). We also used some disaggregation algorithms and mathematical models of emission processes for some categories of human activity:

• for fossil fuel usage (Boychuk and Bun 2014), for electricity and heat production (Topylko et al. 2015), for the transport categories (Boychuk et al. 2012; Valakh et al. 2015), for the residential sector (Danylo et al. 2015), and for industry (Halushchak et al. 2016);

• for emissions from fossil fuel extraction and processing (Halushchak et al. 2015);

• for the industrial, agricultural, and waste sectors (Charkovska et al. 2018a);

• for forestry and land use change (Striamets et al. 2014).

These algorithms are different for each category of human activity. They take into account the available statistics at the corresponding administrative level, and use other parameters that can be considered as indicators or proxy data for disaggregation of the statistical activity data. We always use the activity/proxy data from the lowest administrative level as a rule.

For example, to calculate emissions from the road transport, we take into account the following road categories: national, province/voivodeship, district, and community roads; and the following road types: highway, express route, dual carriageway, express carriageway, dual carriageway for heavy traffic up to 11.5 t per axle, single carriageway for heavy traffic up to 11.5 t per axle, dual carriageway for heavy traffic up to 10 t per axle, single carriageway for heavy traffic up to 10 t per axle, dual carriageway up to 8 t per axle, single carriageway up to 8 t per axle, dual carriageway, single carriageway, other paved surfaces, dirt roads, and city roads. We analyze the following types of vehicles: scooters, motorcycles, cars, buses, and other types of vehicles such as trucks, mobile cranes, and snow plows and use the traffic intensity factors established by experts for these vehicles (Valakh et al. 2015). On this basis, we calculate the amount of gasoline, diesel, and liquefied petroleum gas (LPG) used by different types of vehicles on each segment of the road. Then, we calculate the emissions of carbon dioxide CO₂, methane CH₄, and nitrous oxide N₂O from burning gasoline, diesel, and LPG, separately, for all types of vehicles and for each road segment. Using the global warming potentials of each GHG, we estimate the total emissions from each road segment.

According to this approach, we calculate the emissions of CO₂, CH₄, N₂O, SO₂, CF₄, C₂F₆, NO_x, and NMVOC from all the point, linear, and area sources outlined previously for all categories of activity separately. Based on these results, many different digital maps of emissions can be created, e.g., NO_x emissions from paper production, NO_x emissions from pulp production, NMVOC emissions from pulp production, among many others.

We then calculate the total emissions in CO₂-equivalent using the global warming coefficients. At this stage, we sum the emissions from the point-, line-, and area-type emission sources for each emission category. In order to do this, we overlay a grid on top of the vector layers where each grid cell is a polygon. The grid cells are split by administrative boundaries into separate elementary objects, so that each grid cell retains information about the corresponding administrative units.

The unique aspect of this approach to developing a GHG spatial inventory is the ability to use different emission factors for separate elementary objects (or even for parts of objects), if such data are available, as opposed to using averaged or default values employed in more traditional techniques. This approach is extremely relevant for large emission sources such as electricity and heat production plants, iron and steel production, and cement production, since we can take specific features of technological processes into account such as the applied filters and other equipment as well as the parameters of the fuel used.

In the final stage, the uncertainties of the assessed emissions are estimated using a Monte Carlo approach with symmetric or asymmetric (lognormal) distributions of the investigated parameters to compute the 95% confidence intervals. This estimation can be applied to the separate emission sources as well as to the aggregated results for the administrative units (see block “Analysis of result uncertainties” in Fig. 1).

The emissions in each category of the anthropogenic activity for the elementary objects can be visualized in the form of digital maps using different approaches, depending on the source type. The results of the spatial inventory can also be presented separately for each category of emissions, as well as separately for different fossil fuel types or for different GHGs (see block “Visualisation of results” in Fig. 1).

Since information about the administrative assignment of each elementary object (emission source) is saved in the database, it is possible to aggregate the emissions to administrative units (even for small units like municipalities) without any loss in accuracy as with more traditional techniques of gridded emission, when cells of regular grids are used for the estimation of emissions for small territories without taking into account the administrative boundaries.

Input data

High-resolution maps of emission sources

As mentioned previously, to use the proposed technique for the practical implementation of a GHG spatial inventory, we need high-resolution digital maps of very diverse emission sources, which are treated separately as points, lines, and areas. Examples of point-type emission sources are electricity or combined electricity and heat production plants, cement plants, production of glass, ammonia, iron and steel, aluminum, pulp and paper, petroleum refining, underground mining, etc. (Fig. 2a). Using official information on the addresses of companies in this sector, it is possible to determine the location of their production facilities (i.e., the latitude and longitude) using Google Earth™. As the spatial resolution of Google Earth™ imagery can be several meters to centimeters, the point-type emission sources are very accurate for the purpose of building the spatial inventory of GHG emissions. Exceptions are when power plants consist of multiple stacks. For example, in the Burshtynska power plant (Ukraine), there are three stacks (heights of 250, 250, and 180 m) with distances of around 100 m between them. Although we can accurately locate each stack, it is not possible to split the activity data for these stacks so an average location is chosen to represent point source of this type (i.e., in the case of a power plant with multiple stacks, we still consider it as a single point-type emission source with an averaged longitude and latitude).

Fig. 2

Examples of emission sources for the GHG spatial inventory. a Electricity generation plants as point-type sources. b Roads as line-type sources. c Settlements as area-type sources

Road and railway transport systems represent examples of line-type emission sources (Fig. 2b). To construct maps of these sources, we used the OpenStreetMap (Jokar Arsanjani et al. 2015), which is a community-based map built through a combination of digitizing very high-resolution imagery and paper-based field surveys or surveys undertaken with GPS-enabled devices. The spatial resolution of this source of data is also very high. To retain administrative information, roads and railways are additionally split by administrative boundaries into segments, which we consider as separate elementary objects in the inventory. The number of line objects is equal to the number of roads segments. Information on road category is used as one of the indicators/proxies for disaggregation of the data on fossil fuel combustion by various categories of vehicle in the transport sector. It is taken into account that the intensity of emission depends directly on the intensity of the traffic flow, and the latter depends on the category of a road, as specified earlier. Moreover, these dependencies are different for different types of vehicles (for example, the intensity of truck traffic is small in urban streets) (Valakh et al. 2015). Therefore, the data on vehicles registered by type are also used as proxy data for disaggregation of activity data.

Area-type (or diffused) GHG emission sources or sinks are croplands, settlements, industrial areas, and forests, among others (Fig. 2c). They consist of a large number of small GHG emission sources/sinks that cannot be regarded separately, but as a whole, they can be considered as one emission source/sink within some boundaries. Such area-type objects can be small or large and can be of complicated configuration. In the digital maps, such sources/sinks are represented as polygons for all categories under investigation. The number of such objects is equal to the number of polygons. The objects that correspond to croplands and forests are additionally split by administrative boundaries to retain information on the administrative assignment of the elementary objects. To build these maps, we used Corine Land Cover vector maps (Corine 2006), which were created from raster maps with a resolution of 100 m. This resolution was used for the digital maps of all area-type sources as well as the final spatial resolution of the GHG spatial inventory.

Note that all point-, line-, and area-type sources are treated as vector digital maps, not raster, in order to retain fully the administrative assignment of each object (even at the municipality level), and we use this information for the aggregation of emissions to the corresponding administrative units.

Statistical data for Poland and other proxy data

The GHG spatial inventory for Poland covers an area of 312,679 km², 16 voivodeships/provinces, 379 powiats/districts, and 2478 gminas/municipalities. We downloaded the activity data for different emission categories by province, district, and municipality (where available) from the Central Statistical Office of Poland (GUS 2016) and the Local Data Bank (BDL 2016). Examples include the amount of fossil fuels used, data about production, the number of animals in agriculture, etc., all of which are listed in Table 1. Average national emission factors and the activity data at the national scale were obtained from Poland’s National Inventory Report (NIR 2012).

Table 1 Main GHG emission categories: data used for GHG spatial inventory and proxy data used for disaggregation of activity data to the level of emission sources (types of emission sources: p—point-type emission sources; l—line-type emission sources; a—area-type emission sources)

We also used proxy data for disaggregation of the activity data to the level of elementary objects. Examples of such proxy data are the power of the electricity generation plants (Topylko et al. 2015), population density, data on access to energy sources and the heating degree-days in the residential sector (Danylo et al. 2015), the gross value of production in the industry sector (Charkovska et al. 2018b), car numbers, and road categories in the road transport sector. The full list is provided in Table 1.

In those cases where it was possible, the emission coefficients and parameters that reflect the territorial specificity of the emission and absorption processes were applied in the emissions calculation. For example, when calculating the accumulated carbon in forests, we used the information from the Local Data Bank (BDL 2016) on the species composition, the age structure, etc., at the level of districts/powiats, and municipalities/gminas.

Results

The spatially explicit GHG inventory for Poland

Emission sources

Using the digital maps of the GHG emission sources/sinks in Poland and the algorithms for activity data disaggregation, a geospatial database was created. The GHG emissions/absorptions were then estimated using appropriate mathematical models of emission processes for the fossil fuel usage in electricity and heat production, the transport, the residential sector, the manufacturing industry, the fossil fuel extraction, and the processing; the industrial, agricultural, and waste sectors; and the forestry and land use change.

We calculated GHG emissions (CO₂, CH₄, N₂O, SO₂, CF₄, C₂F₆, NO_x, and NMVOC) for all categories of activity separately. These results were obtained at the level of elementary objects, i.e., the point-, line-, and area-type sources of emissions. Using them, we calculated the total emissions in CO₂-equivalents using the global warming coefficients. As an example, the total GHG emissions in the transport sector by road segment for one Polish province are presented in Fig. 3. We can see there that the segments with the highest emissions (between 756 and 833 Mg/km²) are the national roads E40 and E371. High emissions are also in the Rzeszów agglomeration, which is the capital of this province, while smaller emissions are in the mountainous regions.

Fig. 3

Total GHG emissions in the transport sector by road segment (Subcarpathian province, Mg/km², CO₂-equivalent, 2010)

To calculate these emissions, we took into account the road categories, the road types, the various types of vehicles, and the traffic intensity factors as described in Sect. 2.1. Also we calculated the emissions caused by combustion of gasoline, diesel, and liquefied petroleum gas used by different types of vehicles, separately for carbon dioxide, methane, and nitrous oxide for all types of vehicles and each road segment. The total emissions from each road segment were calculated using the global warming potentials of each GHG.

The road transport in Poland, with 15% of the total GHG emissions in the energy sector, is prevailing among all modes of transport, such as railway, domestic aviation, and shipping. Railways in Poland are heavily electrified, so the share of GHG emissions from this type of transport is only 0.11% of the total emissions in the energy sector. The compact configuration of Poland and its relatively small size make the use of civil aviation for domestic transport inefficient—the share of emissions from domestic aviation is only 0.03% of the energy sector emissions. The configuration of the coastline and relatively small rivers from a transport perspective have resulted in a very small share of domestic shipping (emissions from domestic navigation amount to only 0.0004% of the energy sector emissions). Therefore, these categories hardly influence the spatial pattern of total emissions compared to other more powerful emission sources. Moreover, since our approach is devoted to the spatial analysis of GHG emissions at the regional/national level, we have not investigated emissions from the use of bunker fuels for international transportation.

Similar detailed calculations of GHG emissions, as for the road transport, were done for all categories of anthropogenic emissions considered here. As a result, the spatial distributions of the GHG emissions (separately for the different gases as well as the total) at the level of the point-, line-, and area-type emission sources were obtained. These data for each category of emissions can be downloaded from Supplementary Materials.

In the final stage, the point-, line-, and area-type emission sources for each emission category were summed to calculate the total emissions. For this purpose, we used a grid where each grid cell is represented as a polygon feature. The grid cells were also split by administrative boundaries into separate elementary objects as shown in Fig. 4 so that each grid cell retains information about the administrative assignment. For example, an administrative boundary may split some grid cells into separate elementary objects in the GHG spatial inventory (e.g., objects 2 and 3 as well as objects 4 and 5 in Fig. 4). Then we summed the emissions from all sources that are fully or partly situated within a cell or its administrative unit. Therefore, the emissions from cell 1 are the sum of emissions from two point sources, a segment from a line source, and part of an area source. Emissions from elementary object 2 correspond to part of emissions from an area source, and emissions from objects 3, 4, and 5 correspond to segments of line sources, etc. (Fig. 4). The emission from line-type sources is originally calculated per length unit (for example, Mg/km as in Fig. 3), as emission intensity. To calculate the emissions for the grid, the emission intensity is multiplied by the segment length located within the grid cell (the result is given, for example, in Mg). Then, the emissions from road segments are summed together with emissions from other sources within the cell to provide the total emissions, which may also be conveniently presented as the emission intensity per area unit (for example, Gg/cell as in Fig. 5 or Gg/km² as in Fig. 6).

Fig. 4

Combining diverse GHG emission sources into a grid where the cells are split by administrative boundaries into separate elementary objects of the vector map

Fig. 5

Total GHG emissions in Poland and for the Silesian province (all categories without LULUCF, 2010, Gg/cell area, CO₂-equivalent, 2 km grid size)

Fig. 6

Prism map of specific GHG emissions from all sectors/categories of human activity without LULUCF in Silesian province at the level of elementary objects (CO₂-equivalent, Gg/km², square root scale, 2 × 2 km, 2010)

In this way, the total emissions from all categories can be calculated. Any grid size can be chosen as long as it is larger than 100 m due to the limit of the data used to derive the area-type emission sources. However, for visualization purposes, we used a 2-km grid size.

Figure 5 provides a map of the total GHG emissions for all categories of the energy, industry, agriculture, and waste sectors for Poland and for the Silesian province, which is the most industrialized Polish province. An alternative representation is provided in Fig. 6 for the Silesian province in Poland using a prism map and the square root of the emissions for better visualization of the results. This 3D presentation perfectly illustrates a non-uniform localization of emission sources and the essential differences in the emission magnitudes.

As expected, the results of the calculations showed considerable unevenness in the spatial distribution of GHG emission sources. The largest emissions are caused by point-type sources, including power plants. There are 80 electricity generation plants with power over 20 MW in Poland. In 2010, most of the emissions were caused by Elektrownia Bełchatów SA in Łódź province (abbreviation LDZ in the figures). With an emission of 21,926 Gg_CO2-eq. per year, it is the biggest power plant using coal in Europe. This is followed by Elektrownia Pątnów II in Greater Poland (WKP) province, with an emission of 17,896 Gg_CO2-eq., and Elektrownia Rybnik SA in Silesian (SLK) province, with an emission of 11,630 Gg_CO2-eq.. The emissions for the grid cells with these sources are very large as compared to other grid cells, so it causes substantial difficulties in creating maps of emissions. Hence, we used a non-linear function of the square root for creating these maps. Lower emissions are due to point sources, such as steel mills, oil refineries, and chemical plants. As we can see from Figs. 5 and 6, significant emissions are caused by the agglomerations of Katowice, Warsaw, Kraków, Łódź, Wrocław, and Poznań. Here, the main emission sources are district heat production plants, industrial zones, road and railway networks, and households. The share of line-type emission sources, including road transport, is not large with respect to the total GHG spatial inventory. Major highways and road networks cause emissions in the range of 1–3 Gg_CO2-eq./km². But given their considerable length, their share in the aggregated emissions for provinces is significant. Among the major area-type emission sources, households in the residential sector are the most important (e.g., the largest emissions are 32.2 Gg_CO2-eq./km²).

Municipality/province emissions

As mentioned previously, the total emissions can be calculated for any administrative unit at the level of gmina/municipality, powiat/district, or voivodeship/province without any loss of accuracy. Figure 7 shows the total GHG emissions from fossil fuel use at the level of municipalities in Poland. In 2010, the highest GHG emissions were in Kleszczów municipality in Łódź (LDZ) province (22,081 Gg_CO2-eq.; 99.3% of these emissions are caused by electricity generation), Konin town in the Greater Poland (WKP) province (18,059 Gg_CO2-eq.; 99.1% by electricity generation), Warsaw in Masovian (MAZ) province (17,219 Gg_CO2-eq.; 70.2% by electricity and heat production), Rybnik town in Silesian (SLK) province (12,319 Gg_CO2-eq.; 94.4% by electricity generation), and Płock town in Masovian (MAZ) province (9957 Gg_CO2-eq.; 89.5% by refinery).

Fig. 7

Total GHG emissions from fossil fuel use in all sectors at the level of municipalities (Poland, CO₂-equivalent, 2010)

Figure 8 shows the total GHG emissions by sectors in Poland at a provincial level, while Fig. 9 focuses on emissions in the energy sector, which has the largest influence on total emissions. In 2010, the highest GHG emissions were caused by the most industrialized provinces such as Silesian (SLK, 63,012 Gg_CO2-eq.), Masovian (MAZ, 55,772 Gg_CO2-eq.), Greater Poland (WKP, 42,686 Gg_CO2-eq.), and Lódź (LDZ, 39,282 Gg_CO2-eq.), and the lowest emissions occurred in Lubusz province (LBU, 6295 Gg_CO2-eq.). The energy sector (fossil fuel) dominated the emissions of all provinces, with the share exceeding 50%. The largest share of the energy sector is in Łódź province (LDZ, 87.8%), Silesian province (SLK, 86.7%), and Masovian province (MAZ, 85.3%), while the lowest is in Podlaskie province (PDL, 53.9%). In addition to the traditional dominance of the energy sector in the emission profiles of industrialized countries, the energy sector in Poland consists of significant use of coal for electricity generation and heat production, industry, and residential subsectors. In the energy sector, the highest emissions are caused by electricity generation and centralized heat production. The share of these categories of emissions is the largest in Łódź province (LDZ, 65.5%; 25,731 Gg_CO2-eq.), Greater Poland province (WKP, 55.1%; 23,501 Gg_CO2-eq.), and Silesian province (SLK, 54.7%; 34,471 Gg_CO2-eq.).

Fig. 8

Total GHG emissions by province and sector (Poland, CO₂-equivalent, 2010)

Fig. 9

Total GHG emissions in the energy sector by province and subsector (Poland, Gg, CO₂-equivalent, 2010)

The shares of emissions from manufacturing industries and the construction sector are the highest in Masovian province (MAZ, 14.7%), from the transport sector in Lubusz province (LBU, 30.8%), and from the building sector in Subcarpathian province (PKR, 30.0%). On the other way, the share of fugitive emissions from fuel extraction and fuel processing is essential only in Silesian province (SLK, 14.6%) and Lublin province (LBL, 7.2%).

The share of the industrial sector (chemical transformation of materials) in all provinces is much lower. The largest share is in Lublin province (LBL, 23.3%), Holy Cross province (SWK, 18.3%), and Lesser Poland province (MLP, 12.8%). The largest shares of emissions from the agriculture sector are in Podlaskie province (PDL, 36.9%), Warmian-Masurian province (WMZ, 23.6%), and Lublin province (LBL, 13.9%). The share from the waste sector is approximately the same in all provinces (2.4−7.3%).

Uncertainty analysis

Factors affecting uncertainty at the GHG source level

The variables and parameters used in the GHG inventory are often highly uncertain (IPCC 2001). These uncertainties are associated with a lack of knowledge about emission processes, inaccurate measuring instruments, etc. (Ometto et al. 2015; White et al. 2011). There are a number of potential uncertainties in the GHG spatial inventory produced here, which can arise from the following factors:

• (a) uncertainty in the geolocation of emission sources and sinks;

• (b) uncertainty in the aggregated activity/statistical data;

• (c) uncertainty in the proxy data representation (uncertainty in the spatial disaggregation of the activity data to the level of the elementary objects using disaggregation algorithms and disaggregation coefficients on the basis of some indicators or proxy data);

• (d) uncertainty in the proxy data values;

• (e) uncertainty in the proxy data geolocation;

• (f) uncertainty in the emission factors.

The uncertainty connected with the geolocation of the sources plays an important role in some applications, especially disaggregation of country emissions to develop a gridded emission dataset, transport model simulations, etc. (Hogue et al. 2016, 2018; Oda et al. 2018; Andres et al. 2016; Singer et al. 2014). However, this factor is not considered in this study because the uncertainty in locating the point- and line-type elementary objects is small, especially for big emission sources since we used Google Earth™ and visual inspection of the sources. We created vector maps of emission sources and determined their geographical coordinates very precisely instead of using a raster grid employed in other approaches. Only power plants with multiple stacks can create some problems, where we represent a group of stacks by an average position. This introduces uncertainty in the geolocation but is considered negligible for the purpose of this study. The uncertainty in the location of the area-type (diffused) emission sources/sinks is a function of the minimum mapping unit of the Corine Land Cover maps (Corine 2006), which is 100 m, where the accuracy of this product is 87.82% (Büttner et al. 2012).

Regarding the uncertainty of the input statistical data such as the uncertainty in the calorific values or emission factors, data from various sources (IPCC 2001; NIR 2012; GUS 2016) and other studies (e.g., Hamal (2009)) have been used. For these variables, we used symmetric and asymmetric (lognormal) distributions and 95% confidence intervals (Bun 2009).

As described previously, the algorithms for disaggregation of the activity data are based on certain proxies, the values of which were mostly fixed using statistical data. Therefore, it was assumed that the uncertainties in the proxy data values are the same as for the statistical data used. It was also assumed that relative uncertainties of disaggregated activity data at the level of emission sources are $\sqrt{n}$ times higher than those in the coarse base area, where n is the number of emission sources of certain category during disaggregation of activity data, similar to Hogue et al. (2018); see also Holnicki and Nahorski (2015) for an analysis in another problem. Based on these input uncertainties, we estimated the distributions of the emissions at the level of emission sources using the Monte Carlo method and calculated the mean values and the lower and upper limits of the 95% confidence intervals as uncertainty ranges (as suggested by IPCC (2001)). For point-type sources, we estimated the uncertainty of the results separately for each source.

As we used the activity/proxy data from the lowest administrative level as possible, the depth of disaggregation procedure was low, with essentially rather small values of n, and as a result, it led to much smaller increase of uncertainties at the level of emission sources than in disaggregation from the country level. For some categories of human activities, such as in the residential sector, the uncertainties in the disaggregated data were evaluated by comparison with similar data from other known sources (GUS 2016; BDL 2016). These results are presented in a number of different studies (Topylko et al. 2015; Danylo et al. 2015; Halushchak et al. 2015, 2016; Charkovska et al. 2018a), where the authors also analyzed the sensitivity of the total uncertainty to changes in the separate component uncertainties such as the statistical data, the calorific values, and the emission factors.

Sensitivity analysis of the uncertainty

We used the calculated data on uncertainties at the level of emission sources for estimation of the uncertainty of emissions at grid cell level (as uncertainty of a sum of the emissions from all sources that are fully or partly situated within grid cells). It allowed us to perform additional uncertainty analysis. Figure 10 presents the sensitivity of the uncertainty of GHG emissions from using fossil fuels in Poland as a whole to the uncertainty of the emissions in separate cells, i.e,. the partial derivative ${k}_{sensit.}=\partial {\overline{U}}_{national}/\partial {\overline{U}}_i$, where k_sensit. is the sensitivity factor, ${\overline{U}}_{national}$ is the relative uncertainty of the national emission, ${\overline{U}}_i$ is the relative uncertainty of emission in the i-th grid cell.

Fig. 10

The sensitivity of the overall uncertainty of GHG emissions in the energy sector of Poland to the uncertainty of the results at grid cells (2010, relative units, grid cells 2 × 2 km; in brackets are the number of cells from corresponding range)

For this analysis, we used calculated data on emissions and uncertainties at the grid cell level. These results are mainly intended for a qualitative analysis, because there is no methodology available for precise estimating the uncertainty of emission parameters at the level of grid cells, including uncertainty in the activity data. For this reason, we present the results in relative units in Fig. 10. The map shows the cells with the greatest impact on the overall uncertainty in the inventory results. Of the total number of 79,000 cells, less than 300 cells have an impact on total uncertainty, and only less than 30 cells play a key role. These cells include the big point sources of emissions, especially the biggest power plants (due to very high emissions) and four major refineries (due to high emission of CH₄ with a high uncertainty). The sensitivity factor is the highest for the cell containing the Elektrownia Bełchatów SA power plant in Łódź (LDZ) province (k_{sensit. , Belchat.} = 0.022). For example, when reducing the relative uncertainty of emissions at this plant by 10%, i.e., from ${\overline{U}}_{Belchat.}$ to $0.9{\overline{U}}_{Belchat.}$, the relative uncertainty in the emissions in the energy sector for Poland will be reduced by 0.2235%, which means a reduction of absolute uncertainty of half of the 95% confidence interval to 16.0 Gg.

Uncertainty at the province level

As the number of elementary objects for line- and area-type sources is large (typically tens of thousands, as in the residential or agriculture sectors), we also evaluated the uncertainties of the results and their sensitivity to changes in the uncertainties of the separate sectors/subsectors using the Monte Carlo method, but at the province level. Figure 11 presents the absolute uncertainty of GHG emissions from the main sectors/subsectors at the provincial level. For this analysis, we used data on emissions at the grid cell level but aggregated to provincial level, as well as data on uncertainty of emission parameters for different sectors/subsectors from the NIR (2012). Although the processes of electricity and heat production dominate the total emissions of almost all provinces, according to this analysis their absolute uncertainties play a key role only in Silesian (SLK; a half of 95% confidential interval is 1167 Gg) and Łódź (LDZ; 871 Gg) provinces, which might seem an unexpected result. Instead, in the provinces with a large population, uncertainty in the waste sector plays a key role (Silesian province, SLK—1049 Gg; Masovian province, MAZ—1039 Gg). Similarly, in the provinces with developed livestock and crop production, the agriculture sector plays a key role (Masovian province, MAZ—1588 Gg; Greater Poland province, WKP—1399 Gg; Kuyavian-Pomeranian province, KPM—1108 Gg). This is due to the fact that in the production of electricity and heat, the emission of carbon dioxide dominates, for which the uncertainty is quite small. Instead, in the agriculture and waste sectors, the emissions of methane and nitrous oxide dominate, which have much greater uncertainty, as well as higher coefficients of global warming. The absolute uncertainty in fugitive emissions from fuel production and processing is essential only in the provinces where there are big mines and refineries (Silesian province, SLK—986 Gg; Masovian province, MAZ—599 Gg; Pomeranian province, POM—191 Gg). The contribution of the uncertainties of emissions from fossil fuel use in the manufacturing industry, transport, commercial, and residential sectors to the overall uncertainty is negligible, because the emissions of carbon dioxide dominate here with low uncertainty and low global warming potential (GWP = 1). The uncertainty in the emissions from industrial processes only plays an essential role in the industrialized Silesian province (SLK, 251 Gg) and provinces with big nitrogen plants (Lublin province, LBL—206 Gg; Lesser Poland province, MLP—141 Gg).

Fig. 11

Absolute uncertainty of GHG emissions from the main sectors/subsectors at provincial level (half of the 95% confidence interval; 2010; Gg)

The influence of the abovementioned factors were analyzed separately at the emission sources level for all categories, and then, the results were combined in the grid cells. For the investigation of the dominant components of uncertainty at the grid cell level, the approach presented by Hogue et al. (2018) can be applied. The learning process outlined in Jonas et al. (2018) can also be used for the continual improvement of GHG emission inventories and uncertainties.

Discussion

The results from the spatial inventory of GHG emissions/absorption for Poland demonstrates an unevenness in the processes involved, such as very high emissions in the industrial Silesian province and low emissions in the strongly forested Masurian Lake region. Such unevenness is typical of many categories of anthropogenic activity. A positive aspect is that the spatial inventory enables the display of the real contributions of each territory to the overall emission processes, which can be of interest to authorities and support well-grounded decision-making.

Since the spatial analysis takes into account the territorial specificity of many parameters that affect emissions or removals of GHGs (e.g., the differentiated characteristics of the fossil fuel used in the energy sector, the climatic conditions and the energy sources availability in the residential sector, the species and age composition of forests, and many others), the total inventory results for the province/country as a whole become more precise than the traditional inventory at the national level, which do not take into account any spatial components and province specificity. Differences between the GHG inventory at the national scale (NIR 2012) and the results presented here for the GHG spatial inventory aggregated to the national scale for 2010 are 1.33% for total emissions from fossil fuel use in the energy sector, 5.1% for total emissions from industrial processes, and 7.4% for total emissions from agriculture. Basically, these differences are caused by the use of specific emission factors for different emission sources in our research, as opposed to averaged coefficients, as used in national inventories.

Traditional inventories at the country level are not useful for undertaking any local analyses. To give an example, high spatial resolutions are needed in modeling the local dispersion of emitted gases to enable comparison of their atmospheric concentration with measurements that can be used for the analysis of the reliability of the inventory data. We have compared the results presented here with the very detailed results from another GHG spatial inventory, i.e. the EDGAR Emission Gridmaps (EDGAR 2017) with a resolution of 0.1° × 0.1° (which for Poland equates to a grid size of 7.1 km × 11.1 km). From this grid, we retained only the cells that cover Poland. After removing the border cells and cells on the coastline, we analyzed the remaining 80% of the area that belongs to Poland. We then aggregated the emissions from point- and area-type high-resolution emission sources to a larger grid to match that of EDGAR, which significantly deteriorated the resolution of our spatial GHG inventory. The results of the comparison for the total CO₂ emissions in all sectors for 2010 are shown in Fig. 12. The total emissions in all the cells analyzed are 330,670 Gg (according to the results of NIR (2012) 332,067 Gg). Figure 12 demonstrates the difference between the results of EDGAR (2017) and our results for each cell. In general, one can see a good correspondence between the two sets of results with the exception of a small number of adjacent blue and red cells, which are caused by the inaccurate georeferencing of big point sources of emissions. As shown from the legend, there are around two dozen of such cells. In particular, one can see an example that reflects the differences due to inaccurate georeferencing of the biggest power plant Bełchatów. The stacks of this power plant are displaced by 950 m (CARMA 2017), which assigns this big emission source to another cell, and result in the appearance of adjacent red and blue pixels, respectively. If the cells with large difference due to point emission sources are excluded, then the average difference in all cells is 0.437 Gg, and the mean squared deviation is 17.7 Gg.

Fig. 12

The difference between the results from EDGAR (2017) for Poland and our results, aggregated to a larger grid; in the brackets is the number of cells in the appropriate range; neighboring red and blue cells reflect inaccurate localization of big point sources of emissions (total CO₂ emissions, 2010, Gg)

The results presented here have also been compared with a high-resolution (1 km × 1 km) global fossil fuel CO₂ emission inventory derived using a point source database and satellite observations of nighttime lights (Oda and Maksyutov 2015). The article by Oda et al. (2018) is devoted to this comparison as well as to the analysis of the abovementioned inaccuracy in the geographic location of big point emission sources.

The estimation of uncertainties associated with GHG spatial inventories is a complicated task, because it requires examination of influences from many factors, such as the uncertainty in the geolocation of the emission source, uncertainty in the aggregated activity/statistical data, uncertainty in the proxy data representation, uncertainty in both these data values and their geolocation, and uncertainty in the emission factors. As a result of careful inspection of the input data, some of these uncertainties have been minimized here in comparison to other studies, particularly the uncertainties associated with the location of large point-type emission sources, which according to Hogue et al. (2018) plays an important role in the total uncertainty of the GHG spatial inventory at the grid cell level.

Conclusions

The approach presented in this paper produces a high-resolution GHG spatial inventory composed of point-, line-, and area-type emission sources/sinks. The spatial analysis is carried out directly on these sources as vector features in contrast to more traditional grid-based emission approaches. Consequently, information on the administrative assignment of corresponding emission sources (plants, settlements, road segments, croplands, etc.) is retained, and this, in turn, makes it possible to aggregate the final results to different subnational levels, even down to submunicipality ones, without decreasing the accuracy of the results. The approach also enables the display and analysis of contributions from all territories, even very small ones, to the overall emission process. Moreover, a GHG spatial inventory can be produced for all categories of human activities, for all GHGs and for all fossil fuel types separately, which is important for the analysis of emissions by sector and the subsequent effectiveness of local decision-making on emission reductions. Thus, each value from traditional national inventory reports can be represented spatially in the inventory, which provides a considerable amount of new knowledge about emission processes that is useful for both decision makers and scientists.

The spatial inventory of GHG emissions created here was essentially carried out using a “bottom-up” method although there are “top-down” elements in the assessment, since we disaggregated the available statistical or proxy data to the level of elementary objects, i.e., point-, line-, or area-type sources of GHG emissions/sinks. This technique, therefore, represents a hybrid approach to building a GHG spatial inventory. Moreover, the approach allows for all information, even partial information about the territorial specificity of the emission or absorption processes, to be included, e.g., specific features of the fossil fuels used and local technological parameters can be considered.

The use of vector maps in this study yielded better results in terms of uncertainty as well as usability. The methodology provides an opportunity to utilize high-resolution input maps of point-, line-, and area-type emission sources and keeps this high resolution in the results, which are independent of the grid size, overlapping grids, etc. Consequently, it excludes the source location uncertainty as a component of total uncertainty and provides the possibility to analyze the sensitivity of the total uncertainty to other parameters. The unique feature of using vector maps in our approach is that the results can be directly converted to a raster map with any desired pixel size (greater than 100 m) without additional loss of accuracy caused by intermediate transformations of different rasters.

The approach to the high-resolution spatial inventory of GHG described here, and the results obtained relate to annual emissions. To assess the dynamics of emissions, a time series of annual inventories are needed. Some changes in emission sources or sinks may then be encountered, new ones may appear, and existing ones may disappear. It is not difficult to make the appropriate changes in the vector maps of the emission sources in such cases, provided the relevant information about these sources exist, as the algorithms for the disaggregation of the activity data and the mathematical models of emission processes do not change.

Finally, it should be emphasized that the practical implementation of the approach presented in this article requires additional effort to prepare high-resolution input maps of emission sources and to use additional proxy data. However, the advantage is that we can produce a unique high-resolution GHG spatial inventory that covers all categories of human activity set out in the IPCC methodology, and we can implement measures to reduce the uncertainty of the spatial inventory.