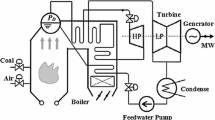
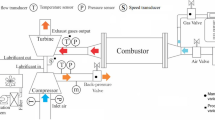
Abstract
Performance control of a boiler–turbine unit is of great importance due to demands for the economical operations of power plants and environmental awareness. In this paper, an optimal control strategy is designed to achieve the desired performance of a boiler–turbine unit. A multivariable nonlinear model of a utility boiler–turbine unit is considered. By manipulation of valves position for the fuel, steam and feed-water flows; output variables including the drum pressure, electric output and fluid density (and consequently drum water level) are controlled. Performance measure of the problem is defined such that the control efforts are minimized while the tracking objectives are obtained. In development of the optimal control strategy, the “variation of extremal” approach is used as an effective tool to handle the nonlinear uncertain problems. Tracking performance of the system is investigated and compared for three cases; tracking from a specific operating point to another ‘near’, ‘far’ and ‘farther’ operating point (depending on the distance between the operating points, the qualitative phrases ‘near’, ‘far’ and farther’ are used). According to the results obtained, more control efforts are required for the tracking of farther operating points (generally). Also, it is investigated that the designed optimal controller guarantees the robust performance of the system in the presence of model parametric uncertainties.














Similar content being viewed by others
Abbreviations
- \( {\bar{\mathbf{a}}} \) :
-
Nonlinear function in state space
- a cs :
-
Steam quality
- \( H_{\infty } \) :
-
H-infinity robust technique
- H :
-
Hamiltonian function
- I :
-
Identity matrix
- J :
-
Performance measure (objective function)
- p i :
-
i-th Component of P (i = 1, 2, 3)
- P :
-
Co-state vector
- \( {\tilde{\mathbf{P}}}_{{\mathbf{x}}} \) :
-
State influence matrix
- \( {\tilde{\mathbf{P}}}_{{\mathbf{p}}} \) :
-
Co-state influence matrix
- q e :
-
Evaporation rate (kg/s)
- q i :
-
i-th Component of Q (i = 1, 2, 3)
- Q :
-
A real symmetric positive semi-definite matrix
- r i :
-
i-th Component of R (i = 1, 2, 3)
- R :
-
A real symmetric positive definite matrix
- t :
-
Time (s)
- t 0 :
-
Initial time
- t f :
-
Final time
- u 1 :
-
Valve position of fuel flow
- u 2 :
-
Valve position of steam control
- u 3 :
-
Valve position of feed-water flow
- \( u_{i}^{*} \) :
-
Optimal control signals in terms of state and co-state variables (i = 1, 2, 3)
- U :
-
Control input vector
- x i :
-
i-th State variable
- X :
-
State vector
- X d :
-
Desired state vector
- y 1 :
-
Drum pressure (kg f/cm2) (y 1 = x 1)
- y 2 :
-
Electric output (MW) (y 2 = x 2)
- y 3 :
-
Fluid density (kg/m3) (y 3 = x 3)
- y 4 :
-
Drum water level (m)
- \( y_{i}^{(j)} \) :
-
Output y i at the operating point # j
- δ :
-
Parameter taking a small value
- \( \psi_{i} \) :
-
A nonlinear function (i = 1, 2)
References
Tan W, Marquez HJ, Chen T, Liu J (2005) Analysis and control of a nonlinear boiler–turbine unit. J Process Control 15:883–891
Tan W, Fang F, Tian L, Fu C, Liu J (2008) Linear control of a boiler–turbine unit: analysis and design. ISA Trans 47:189–197
Donate PD, Moiola JL (1994) Model of a once-through boiler for dynamic studies. Latin Am Appl Res 24:159–166
Lo KL, Zeng PL, Marchand E, Pinkerton A (1990) Modelling and state estimation of power plant steam turbines. IEEE Proc Part C 137(2):80–94
Murty VV, Sreedhar R, Fernandez B, Masada GY, Hill AS (1993) Boiler system identification using sparse neural networks. In: Proceedings of ASME Winter Meeting, New Orleans, pp 103–111
Astrom KJ, Eklund K (1972) A simplified nonlinear model of a drum boiler turbine unit. Int J Control 16(1):145–169
Rink R, White D, Chiu A, Leung R (1996) SYNSIM: A computer simulation model for the Mildred Lake steam/electrical system of Syncrude Canada Ltd. University of Alberta, Edmonton
Adam EJ, Marchetti JL (1999) Dynamic simulation of large boilers with natural recirculation. J Comput Chem Eng 23:1031–1040
Kim H, Choi S (2005) A model on water level dynamics in natural circulation drum-type boilers. Int Commun Heat Mass Transf 32:786–796
Kouadri A, Namoun A, Zelmat M (2013) Modelling the nonlinear dynamic behaviour of a boiler–turbine system using a radial basis function neural network. Int J Robust Nonlinear Control 24:1873–1886
Rusinowski H, Stanek W (2007) Neural modelling of steam boilers. J Energy Convers Manag 48:2802–2809
Moon UC, Lee KY (2011) An adaptive dynamic matrix control with fuzzy-interpolated step-response model for a drum-type boiler–turbine system. IEEE Trans Energy Convers 26(2):393–401
Bell RD, Astrom KJ (1987) Dynamic models for boiler–turbine-alternator units: data logs and parameter estimation for a 160 MW unit. In: Technical Report LUTFD2/(TFRT-3192)/1-137; Department of Automatic Control, Lund Institute of Technology, Lund, Sweden
Astrom KJ, Bell RD (2000) Drum-boiler dynamics. J Autom 36:363–378
Li C, Zhou J, Li Q, An X, Xiang X (2010) A new T–S fuzzy-modeling approach to identify a boiler–turbine system. Expert Syst Appl 37(3):2214–2221
Liu XJ, Kong XB, Hou GL, Wang JH (2013) Modeling of a 1000 MW power plant ultra super-critical boiler system using fuzzy-neural network methods. Energy Convers Manag 65:518–527
Collazo J, Porteiro J, Míguez JL, Granada E, Gómez MA (2012) Numerical simulation of a small-scale biomass boiler. Energy Convers Manag 64:87–96
Bracco S, Troilo M, Trucco A (2009) A simple dynamic model and stability analysis of a steam boiler drum. Proc Inst Mech Eng Part A: J Power Energy 223(7):809–820
Aranda E, Frye M, Chunjiang Q (2008) Model development, state estimation, and controller design of a nonlinear utility boiler system. In: Proceedings of the IEEE International Conference on Industrial Technology (ICIT’08), Sichuan University, Chengdu, China, Article # 4608412, pp 1–6
Kouprianov VI, Kaewboonsong W (2004) Modeling the effects of operating conditions on fuel and environmental costs for a 310 MW boiler firing fuel oil. Energy Convers Manag 45(1):1–14
Yang S, Qian C (2009) Real-time optimal control of a boiler–turbine system using pseudospectral methods. In: 19th Annual Joint ISA POWID/EPRI Controls and Instrumentation Conference and 52nd ISA POWID Symposium, Rosemont, Illinois, USA, Article # 477, pp 166–177
Liu H, Li S, Chai T (2003) Intelligent decoupling control of power plant main steam pressure and power output. Int J Electr Power Energy Syst 25(10):809–819
Liu X, Kong X (2013) Nonlinear fuzzy model predictive iterative learning control for drum-type boiler–turbine system. J Process Control 23(8):1023–1040
Prokhorenkov AM, Sovlukov AS (2002) Fuzzy models in control systems of boiler aggregate technological processes. J Comput Stand Interfaces 24:151–159
Kocaarslan I, Ertuğrul C, Tiryaki H (2006) A fuzzy logic controller application for thermal power plants. J Energy Convers Manag 47:442–458
Thangavelusamy D, Ponnusamy I (2013) Elimination of chattering using fuzzy sliding mode controller for drum boiler turbine system. Control Eng Appl Inform 15(2):78–85
Eitelberg E, Boje E (2004) Water circulation control during once-through boiler start-up. J Control Eng Pract 12:677–685
Li D, Chen T, Marquez HJ, Gooden RK (2006) Life extending control of boiler–turbine systems via model predictive methods. J Control Eng Pract 14:319–326
Chen PC, Shamma JS (2004) Gain-scheduled l 1-optimal control for boiler–turbine dynamics with actuator saturation. J Process Control 14:263–277
Yu T, Chan KW, Tong JP, Zhou B, Li DH (2010) Coordinated robust nonlinear boiler–turbine-generator control systems via approximate dynamic feedback linearization. J Process Control 20:365–374
Abdennour A (2000) An intelligent supervisory system for drum type boilers during severe disturbances. J Electr Power Energy Syst 22:381–387
Nanhua Y, Wentong M, Ming S (2006) Application of adaptive Gray predictor based algorithm to boiler drum level control. J Energy Convers Manag 47:2999–3007
Fang F, Wei L (2011) Backstepping-based nonlinear adaptive control for coal-fired utility boiler–turbine units. J Appl Energy 88:814–824
Moradi H, Bakhtiari-Nejad F, Saffar-Avval M (2009) Robust control of an industrial boiler system; a comparison between two approaches: sliding mode control & H ∞ technique. J Energy Convers Manag 50:1401–1410
Moradi H, Alasty A, Bakhtiari-Nejad F (2007) Control of a nonlinear boiler–turbine unit using two methods: gain scheduling and feedback linearization. In: 2007 ASME international mechanical engineering congress and exposition, IMECE2007-42945, November 11–15, Seattle, Washington, USA
Tan W, Marquez HJ, Chen T (2002) Multivariable robust controller design for a boiler system. IEEE Trans Control Syst Technol 10(5):735–742
Moradi H, Saffar-Avval M, Bakhtiari-Nejad F (2012) Sliding mode control of drum water level in an industrial boiler unit with time varying parameters: a comparison with H ∞ robust control approach. J Process Control 22(10):1844–1855
Moradi H, Bakhtiari-Nejad F (2011) Improving boiler unit performance using an optimum robust minimum-order observer. J Energy Convers Manag 52(3):1728–1740
Kirk DE (1998) Optimal control theory. Dover Publications Inc., Mineola
Moradi H, Alasty A, Saffar-Avval M, Bakhtiari-Nejad F (2013) Multivariable control of an industrial boiler–turbine unit with nonlinear model: a comparison between gain scheduling and feedback linearization approaches. Trans B: Mech Eng J Sci Iran 20(5):1485–1498
Acknowledgments
The authors acknowledge the ‘National Elite Foundation of Iran’ for supporting this research.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
There is no conflict of interest.
Appendix
Appendix
Using Eq. (6), coefficients of state and co-state influence matrices (\( {\tilde{\mathbf{P}}}_{{\mathbf{x}}} \) and \( {\tilde{\mathbf{P}}}_{{\mathbf{p}}} \)) in Eq. (12) are evaluated as:
where,
Rights and permissions
About this article
Cite this article
Moradi, H., Vossoughi, G. Multivariable optimal control of an industrial nonlinear boiler–turbine unit. Meccanica 51, 859–875 (2016). https://doi.org/10.1007/s11012-015-0259-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-015-0259-0