Mathematical modeling of three equal collinear cracks in an orthotropic solid

Abstract

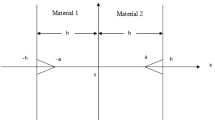
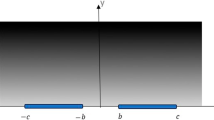
We consider a homogeneous elastic, orthotropic solid containing three equal collinear cracks, loaded in tension by symmetrically distributed normal stresses. Following Guz’s representation theorem and solving Riemann–Hilbert problems we determine the expressions of the complex potentials. Using the asymptotic analysis, we obtain the asymptotic values of the incremental stress and displacement fields. We determine the tangential stresses near the crack tips. Using the maximum tangential stress criterion and numerical computations we study the interaction problem for a Graphite-epoxy fiber reinforced composite material.

Appendix

From (2.2) we get that $\varPhi _j(z_j)$ can be multivalued even if $\varPsi _j(z_j), j=1,2$ are univalued. Consequently, to assure the uniformity of the displacement fields, we must guarantee the uniformity of the potentials $\varPhi _j(z_j), j=1,2$ on closed path around the two cracks.

We denote by U and V the crack tips and by $\varLambda$ and $\varLambda _j$ the corresponding simple closed curves around the crack (U, V) in the complex planes $z=x_1+ix_2$ and respectively $z_j=x_1+\mu _j x_2, j=1,2$.

According to the relations (2.1) and (2.2) the uniformity of $u_1$ is assured if the potentials $\varPsi _j(z_j), j=1,2$ satisfy the restriction:

$$\begin{aligned} \sum _{j=1}^2 \oint _{\varLambda _j} \left( b_j \varPsi _j(z_j)dz_j + \overline{b_j \varPsi _j(z_j)dz_j} \right) = 0. \end{aligned}$$

(5.1)

Taking into account that the integrals involved in (5.1) rest unchanged if $\varLambda$ and $\varLambda _j, j=1,2$ are changed, and squeezing the curve $\varLambda$ around the crack we obtain that the restriction (5.1) is equivalent to the following one:

$$\begin{aligned} {\text {Re}} \left\{ \int _U^V \left( b_1 \varPsi _1^{+}(t) + b_2 \varPsi _2^{+}(t) \right) dt + \int _U^V \left( b_1 \varPsi _1^{-}(t) + b_2 \varPsi _2^{-}(t) \right) dt \right\} = 0. \end{aligned}$$

(5.2)

Using the relations (2.27) and (2.28), the uniformity of $u_1$ will be assured if and only if the following condition is satisfied for all three cracks:

$$\begin{aligned} \int _U^V \left( b_1 \varPsi _1^{+}(t) + b_2 \varPsi _2^{+}(t) \right) dt = \frac{\varGamma _0}{2} \left\{ p \int _U^V \left( \frac{Q(t)}{i \chi (t)} - 1 \right) dt + \int _U^V\frac{P(t)}{i \chi (t)} dt \right\} , \end{aligned}$$

(5.3)

where $\varGamma _0$ and the polynomial Q(t) [see (2.28) for coefficients] are given by:

$$\begin{aligned} \varGamma _0 = \frac{b_1\mu _2 - b_2\mu _1}{\varDelta }, \quad Q(t) = \alpha _3 t^3 + \alpha _2 t^2 + \alpha _1 t + \alpha _0. \end{aligned}$$

(5.4)

We have (see [2, 11]):

$$\begin{aligned} {\text {Im}} \varGamma _0 = 0. \end{aligned}$$

(5.5)

Since, the limit values $\varPsi _1^{-}(t)$ and $\varPsi _2^{-}(t)$ satisfies the equations

$$\begin{aligned} \varPsi _j^{-}(t) = -\varPsi _j^{+}(t) \end{aligned}$$

(5.6)

we can conclude that the condition (5.3) is fulfilled for all three cracks.

The uniformity of $u_2$ is assured if the condition will be satisfied

$$\begin{aligned} \sum _{j=1}^2 \oint _{\varLambda _j} \left( c_j \varPsi _j(z_j)dz_j + \overline{c_j \varPsi _j(z_j)dz_j} \right) = 0. \end{aligned}$$

(5.7)

The above condition is fulfilled if we have satisfied the relations

$$\begin{aligned} \int _U^V \frac{p Q(t) + P(t)}{\chi (t)} dt = 0, \end{aligned}$$

(5.8)

for all three cracks, or, in the equivalent form:

$$\begin{aligned} \int _{-(n+2)a}^{-na}\frac{P(t)}{\chi (t)}dt = - p \int _{-(n+2)a}^{-na}\frac{Q(t)}{\chi (t)} , \;\;\;\; \int _{-a}^{a}\frac{P(t)}{\chi (t)}dt = - p \int _{-a}^{a}\frac{Q(t)}{\chi (t)} , \;\;\;\;\nonumber \\ \int _{na}^{(n+2)a}\frac{P(t)}{\chi (t)}dt = - p \int _{na}^{(n+2)a}\frac{Q(t)}{\chi (t)} \end{aligned}$$

(5.9)

where we denoted by P(t) the polynomial:

$$\begin{aligned} P(t) = C_2 t^2 + C_1 t + C_0. \end{aligned}$$

(5.10)

Denoting by

$$\begin{aligned} I_k = \int _{-a}^a \frac{t^k}{\chi (t)} dt, \;\;\; J_k = \int _{na}^{(n+2)a} \frac{t^k}{\chi (t)} dt \end{aligned}$$

(5.11)

observe that

$$\begin{aligned} \int _{-(n+2)a}^{-na} \frac{t^k}{\chi (t)}dt = (-1)^k J_k , \end{aligned}$$

(5.12)

and

$$\begin{aligned} I_{2k+1} = 0 , \;\;\; k = 0, 1, 2, \ldots \end{aligned}$$

(5.13)

with (2.28) the restrictions (5.10) take the following system of algebraic equations:

$$\begin{aligned}&J_0 C_0 - J_1 C_1 + J_2 C_2 = p (J_3 + \alpha _1 J_1) \nonumber \\&I_0 C_0 + I_2 C_2 = 0\nonumber \\&J_0 C_0 + J_1 C_1 + J_2 C_2 = -p (J_3 + \alpha _1 J_1) . \end{aligned}$$

(5.14)

Solving the above system, we get the following values for the coefficients $C_0, C_1$ and $C_2$ of the polynomial P(z):

$$\begin{aligned} C_0 = 0, C_1 = - p \left( \frac{J_3}{J_1} + \sigma _1 \right) , C_2 = 0. \end{aligned}$$

(5.15)