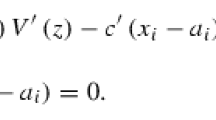Multi-player, Multi-prize, Imperfectly Discriminating Contests

Abstract

This paper models success probability in imperfectly discriminating contests involving multiple players and multiple prizes. This, in fact, turns out to be a generalization of Tullock’s contest success function to a multi-player, multiple prizes. The model can be used to analyze efforts exerted by individuals in various real-life situations, like obtaining seats in congested public transportation vehicles or obtaining admission into elite educational institutes. We propose a “holistic” probability model, derive the equilibrium efforts exerted, and analyze those efforts, the associated total costs and total dissipation, and explore pricing and number of ‘seats’. The derivation provides a new rational for the multinomial Logit Model. It also derives formula for rent dissipation. We also discuss two extensions of the model.

Appendices

Appendix A: Derivation of the Probability Model with an Example

Consider the basic probability model with $\lambda = 0$. Let $n \quad =$ 3, $\bar {n} \quad =$ 2. Then the possible outcomes and associated probabilities are as follows:

$$\bar{{\upsilon} }_{1} =(1,1,0):\,p_{1} =K\,(\varepsilon_{1} (\bar{{\upsilon} }_{1} )\,e_{1} +\varepsilon_{2} \,(\bar{{\upsilon} }_{1} )\,e_{2} +\varepsilon_{3} \,(\bar{{\upsilon} }_{1} )\,e_{3} )=K\,(e_{1} +e_{2} ) $$

$$\bar{{\upsilon} }_{2} =(1,0,1):\,p_{2} =K\,(\varepsilon_{1} (\bar{{\upsilon} }_{2} )\,e_{1} +\varepsilon_{2} \,(\bar{{\upsilon} }_{2} )\,e_{2} +\varepsilon_{3} \,(\bar{{\upsilon} }_{2} )\,e_{3} )=K\,(e_{1} +e_{3} ) $$

$$\bar{{\upsilon} }_{3} =(0,1,1):\,p_{3} =K\,(\varepsilon_{1} (\bar{{\upsilon} }_{3} )\,e_{1} +\varepsilon_{2} \,(\bar{{\upsilon} }_{3} )\,e_{2} +\varepsilon_{3} \,(\bar{{\upsilon} }_{3} )\,e_{3} )=K\,(e_{2} +e_{3} ) $$

Hence summing over all outcomes we get,

$$1=p_{1} +p_{2} +p_{3} =K\,\ast \,\sum\limits_{i = 1}^3 e_{i} \,\left( {\sum\limits_{\bar{{\upsilon} }\in {\Omega}}{\varepsilon_{i}}(\bar{{\upsilon} })} \right) $$

$$=K\,\ast \left( {e_{1} \left( {\sum\limits_{\bar{{\upsilon} }\in {\Omega}} {\varepsilon_{1}}(\bar{{\upsilon} })} \right)+e_{2} \,\left( {\sum\limits_{\bar{{\upsilon} }\in {\Omega}} {\varepsilon_{2}}(\bar{{\upsilon} })} \right)+e_{3} \left( {\sum\limits_{\bar{{\upsilon} }\in {\Omega}}{\varepsilon_{3}}(\bar{{\upsilon} })} \right)} \right)\, $$

Now

$$\sum\limits_{\bar{{\upsilon} }\in {\Omega}} {\varepsilon_{1} (\bar{{\upsilon} })} =\sum\limits_{{\begin{array}{*{20}c} {\bar{{\upsilon} }\in {\Omega}} \hfill \\ {\varepsilon_{1} (\bar{{\upsilon} })= 1} \hfill \end{array}} } 1 = 2 $$

$$\sum\limits_{\bar{{\upsilon} }\in {\Omega}}{\varepsilon_{2} (\bar{{\upsilon} })}=\sum\limits_{{\begin{array}{*{20}c} {\bar{{\upsilon} }\in {\Omega}} \hfill \\ {\varepsilon_{2} (\bar{{\upsilon} })= 1} \hfill \end{array}} }1 = 2 $$

$$\sum\limits_{\bar{{\upsilon} }\in {\Omega}}{\varepsilon_{3} (\bar{{\upsilon} })} =\sum\limits_{{\begin{array}{*{20}c} {\bar{{\upsilon} }\in {\Omega}} \hfill \\ {\epsilon_{3} (\bar{{\upsilon} })= 1} \hfill \end{array}} } 1 = 2. $$

Hence substituting we get

$$1=K\,\ast \,2\,\ast \,(e_{1} +e_{2} +e_{3} ). $$

And $2=\left ({\begin {array}{l} 3 \\ 2 \end {array}} \right )$, for this example.

Now consider an example with $n = 3,\,\bar {{n}}= 2,\,e_{1} = 8,\,e_{2} =e_{3} = 1$. Then we get the following:

$$P_{1} =\frac{1}{2}+\frac{8}{10}\,\frac{1}{2\,}=\frac{18}{20} $$

$$P_{2} =\frac{1}{2}+\frac{1}{10}\,\frac{1}{2\,}=\frac{11}{20} $$

$$P_{3} =\frac{1}{2}+\frac{1}{10}\,\frac{1}{2\,}=\frac{11}{20}. $$

Again the sum equals $\bar {{n}}= 2$. This means (roughly) that person 1 exerting high effort gets to sit with a very high probability in one of the seats, while the other two people exerting the same low probability gets to sit with almost equal probability in the remaining 1 seat.

Appendix B: Proof of Proposition 2

Proof

We can write the objective function as:

$$C_{i} (e_{i} ,e_{-i} ;n)=g(n-\bar{{n}})+[\bar{{c}}-g(n-\bar{{n}})]\,P_{i} +\chi_{i} \frac{e_{i}^{\alpha + 1}} {\alpha + 1}. $$

Now$P_{i}=\frac {\bar {{n}}-1}{n-1}\mathrm {+} \left [ {\frac {n-\bar {{n}}}{n-1}} \right ]\,\,\left [{\frac {e_{i}} {\sum \limits _j {e_{j}} } } \right ].$

Therefore we can rewrite the objective function as

$$C_{i} (e_{i} ,e_{-i} ;n)=g(n-\bar{{n}})+[\bar{{c}}-g(n-\bar{{n}})]\,\left[ {\frac{\bar{{n}}-1}{n-1}} \right] $$

$$+[\bar{{c}}-g(n-\bar{{n}})]\,\left[ {\frac{n-\bar{{n}}}{n-1}} \right]\,\,\left[ {\frac{e_{i}} {\sum\limits_j{e_{j}} } } \right]\,+\chi_{i} \,\frac{e_{i}^{\alpha + 1}} {\alpha + 1}. $$

Consider a change of variable $e_{i} =\exp \,(E_{i} )$,so that

$$\text{P}_{i} =\frac{\exp \,(E_{i} )}{\sum\limits_j{\exp} \,(E_{j} )} $$

Alsolet

$$\overset{\frown}{c} =\left[ {g(n-\bar{{n}})\,\frac{n-\bar{{n}}}{n-1}\,+\bar{{c}}\,\frac{\bar{{n}}-1}{n-1}} \right] $$

$$\omega =[g(n-\bar{{n}})\,-\bar{{c}}]\,\frac{n-\bar{{n}}}{n-1}. $$

Hence the objective function can be written

$$C_{i} (E_{i} ,E_{-1} ;n)=\hat{{c}}-\omega P_{i} +\frac{\chi_{i}} {\alpha + 1}\,\exp \,[(\alpha + 1)\,E_{i} ]. $$

Therefore, the F.O.C.s are

$$ \frac{\partial C_{i} \,(E_{i} ,E_{-i} ;n)}{\partial E_{i}} =-\omega P_{i} (1-P_{i} )+\chi_{i} \,\exp \,[(\alpha + 1)\,E_{i} ]= 0. $$

(23)

Thus Eq. 23 defines the best reply of agent i, with respect to the strategy of the other agents,$E_{i}^{br}$.

Now assuming $\chi _{i} =\chi \forall _{i}$, we get the symmetric Nash equilibrium as follows (refer to appendix C for the asymmetricsolution):

$$\exp \,[E^{\ast} ]=e^{\ast} =\left[ {\frac{\omega} {\chi} \left( {\frac{n-1}{n^{2}}} \right)} \right]^{\frac{1}{\alpha + 1}} $$

or

$$e^{\ast} =\left[ {\frac{1}{\chi} \,\,\left( {\frac{n-\bar{{n}}}{n^{2}}} \right)\,\,[g(n-\bar{{n}})-\bar{{c}}]} \right]^{\frac{1}{\alpha + 1}}. $$

The S.O.C.s are (which are true even for the asymmetriccase):

$$\frac{\partial^{2}C_{i} \,(E_{i} ,E_{-i} ;n)}{\partial E_{i}^{2}} =-\omega (1-2P_{i} )\,P_{i} (1-P_{i} )+\chi_{i} \,(\alpha + 1)\,\exp \,[(\alpha + 1)\,E_{i} ]. $$

Substituting the F.O.C. in the S.O.C., we get,

$$\frac{\partial^{2}C_{i} \,(E_{i} ,E_{-i} ;n)}{\partial E_{i}^{2}} \left|{{~}_{f.o.c} =} \right.-\omega (1-2P_{i} )\,P_{i} (1-P_{i} )+\,(\alpha + 1)\,\omega \,P_{i} (1-P_{i} ) $$

$$=\,\omega P_{i} \,(1-P_{i} )\,[-(1-2P_{i} )+(\alpha + 1)] $$

$$=\omega \,P_{i} (1-P_{i} )\,[2P_{i} +\alpha ]. $$

For convexity of the objective function, we need the above expression to be positive. Therefore, a sufficient condition wouldbe $[2P_{i} +\alpha ]>0$, for any$P_{i}$. For this,$\alpha >0$ is a sufficient condition.

In the symmetric case, the condition becomes,$\left [ {\frac {2}{n}+\alpha } \right ]>0$ which reducesto $\alpha >-\frac {2}{n}.$ Forvery large n, this implies again that the cost function is convex.

Uniqueness. The condition for uniqueness is

$$\underset{j\ne i}{\sum\limits_{j = 1,\mathellipsis N,}} \left| {\frac{\partial E_{i}^{br}} {\partial E_{j}} } \right|<1. $$

Let

$${\Omega}_{i} =-\omega P_{i} (1-P_{i} )+\chi_{i} \,\exp \,[(\alpha + 1)\,E_{i} ]= 0. $$

Thus, by the implicit function theorem, weget,

$$\frac{\partial E_{i}^{br}} {\partial E_{j}} =-\frac{\partial {\Omega}_{i} /\partial E_{j}} {\partial {\Omega}_{i} /\partial E_{i}} $$

$$=-\frac{\omega \,(2P_{i} -1)\,P_{i} P_{j}} {-\omega \,(1-2P_{i} )\,P_{i} (1-P_{i} )+\chi_{i} (\alpha + 1)\,\exp \,[(\alpha + 1)\,E_{i} ]} $$

$$=\frac{P_{j} \,(2P_{i} -1)}{(1-P_{i} )\,\,(2P_{i} +\alpha )}. $$

Hence

$$\left| {\frac{\partial E_{i}^{br}} {\partial E_{j}} } \right|= \frac{P_{j} \,\left| {2P_{i} -1} \right|}{(1-P_{i} )\,\,(2P_{i} +\alpha )}. $$

Hence summing over all $j\ne i$, weget

$$\underset{j\ne i}{\sum\limits_{j = 1,\mathellipsis N,}}\left| {\frac{\partial E_{i}^{br}} {\partial E_{j}} } \right|=\frac{\left| {2P_{i} -1} \right|}{2P_{i} +\alpha} $$

which is a decreasing function of $\alpha$. Hence, for$\alpha =-1,$

$$\underset{j\ne i}{\sum\limits_{j = 1,\mathellipsis N,}}\left| {\frac{\partial E_{i}^{br}} {\partial E_{j}} } \right|= 1 $$

And$\forall \alpha >-1$,

$$\underset{j\ne i}{\sum\limits_{j = 1,\mathellipsis N,}}\left| {\frac{\partial E_{i}^{br}} {\partial E_{j}} } \right|<1. $$

This proves uniqueness and the proposition. □

Appendix C: Asymmetric Case

We can write the objective function as follows (notice $\bar {{c}}_{i}$ instead of $\bar {{c}},g_{i} (\cdot )$ instead of $\bar {{c}},g({\cdot })$, ${\alpha _{i}}$ instead of ${\alpha }$, and $\chi _{i}$ instead of $\chi$, as costs for individual $i)$:

$$C_{i} (e_{i} ,e_{-i} ;n)=g_{i} (n-\bar{{n}})+[\bar{{c}}_{i} -g_{i} (n-\bar{{n}})]\,P_{i} +\chi_{i} \,\frac{e_{i}^{\alpha_{i} + 1}} {\alpha_{i} + 1} $$

Recall

$$P_{i} =\frac{\bar{{n}}-1}{n-1}+\frac{n-\bar{{n}}\,}{n-1}\frac{e_{i}} {\,\sum\limits_j{e_{j}} } . $$

Like before, with $e_{i} =\exp \,(E_{i} )$ and

$$P_{i} =\frac{\exp \,(E_{i} )}{\sum\limits_j{\exp} \,(E_{j} )}, $$

$$\hat{{c}}_{i} =\left[ {g_{i} (n-\bar{{n}})\,\frac{n-\bar{{n}}}{n-1}+\bar{{c}}_{i} \frac{\bar{{n}}-1}{n-1}} \right], $$

$$\omega_{i} =\left[ {g_{i} (n-\bar{{n}})-\bar{{c}}_{i}} \right]\,\frac{n-\bar{{n}}}{n-1}, $$

we get

$$C_{i} (E_{i} ,E_{-1} ;n)=\hat{{c}}_{i} -\omega_{i} P_{i} +\frac{\chi_{i}} {\alpha_{i} + 1}\,\exp \,[(\alpha_{i} + 1)\,E_{i} ]. $$

Therefore, the F.O.C.s are:

$$ \frac{\partial C_{i} \,(E_{i} ,E_{-i} ;n)}{\partial E_{i}} =-\omega_{i} P_{i} \,(1-P_{i} )\,\,+\,\chi_{i} \exp \,[(\alpha_{i} + 1)\,E_{i} ]= 0. $$

(24)

That is,

$$\omega_{i} P_{i} (1-P_{i} )=\chi_{i} \,\exp \,[(\alpha_{i} + 1)\,E_{i} ]. $$

Let ${\Phi } =\sum \limits _j {\exp \,(E_{j} )} =\sum \limits _j{e_{j}} .$ Then, we get

$$0=\omega_{i} \frac{\exp \,(E_{i} )}{\Phi} \,\,\,\left( {1-\frac{\exp \,(E_{i} )}{\Phi} } \right)-\chi_{i} \,[\exp \,(E_{i} )]^{\alpha_{i} + 1} $$

$$=\omega_{i} \exp \,(E_{i} )\,({\Phi} -\exp \,(E_{i} ))-{\Phi}^{2}\,\chi_{i} \,[\exp \,(E_{i} )]^{\alpha_{i} + 1}_{\mathrm{.}} $$

Since $e_{i} =\exp \,(E_{i} )$, the F.O.C. becomes:

$$\omega_{i} \,({\Phi} -e_{i} )e_{i} -{\Phi}^{2}\chi_{i} \,(e_{i} )^{\alpha_{i} + 1}= 0 $$

$${\Phi}^{2}\chi_{i} \,(e_{i} )^{\alpha_{i} + 1}+\omega_{i} (e_{i} )^{2}-{\Phi} \,\omega_{i} e_{i} = 0 $$

The first-order condition, simplifies as follows:

$$(e_{i} )^{\alpha_{i}} +\frac{\omega_{i} e_{i}} {\chi_{i} {\Phi}^{2}}-\frac{\omega_{i}} {\Phi \chi_{i}} = 0 $$

If $\alpha _{i} = 0\forall i:$We have $\frac {\omega _{i}} {\chi _{i}} \frac {e_{i}} {{\Phi }^{2}}=\frac {\omega _{i}} {\Phi \chi _{i}} -1,\,or\,\,\frac {\omega _{i}} {\chi _{i}} ={\Phi } -{\Phi }^{2}\,\frac {\chi _{i}} {\omega _{i}}$

$$e_{i} \,=\left( {1-{\Phi} \frac{\chi_{i}} {\omega_{i}} } \right)\,{\Phi} . $$

Thus:

$$\sum\limits_{j} e_{j} ={\Phi} \sum\limits_j \left( {1-{\Phi} \frac{\chi_{i}} {\omega_{i}} } \right)={\Phi} \,\left( {n-{\Phi} \sum\limits_{j} \frac{\chi_{j}} {\omega_{j}} } \right)={\Phi} ; $$

$${\Phi} =\frac{(n-1)}{\sum\limits_j {\frac{\chi_{j}} {\omega_{j}} }} $$

$$e_{i}^{\ast} =\left( {1-\frac{(n-1)\,\frac{\chi_{i}} {\omega_{i}} }{\sum\limits_j {\frac{\chi_{j}} {\omega_{j}} }} } \right)\,\,\,\,\frac{(n-1)}{\sum\limits_j {\frac{\chi_{j}} {\omega_{j}} }} $$

The following proposition summarizes our findings in the asymmetric case.

Proposition 1

Consider asymmetric but linear cost of effort, that is, cost of effort of individual i is given by$\chi _{i}e_{i} ,\,\forall _{i}$.Let$\omega _{i} =\left [{g_{i} \,(n-\bar {{n}})-\bar {{c}}_{i}} \right ]\,\frac {n-\bar {{n}}}{n-1}$. Then the Nash equilibrium level of effort of individual i is given by

$$ e_{i}^{\ast} =\left( {1-\frac{(n-1)\frac{\chi_{i}} {\omega_{i}} }{\sum\limits_j \frac{\chi_{j}} {\omega_{j}} }} \right)\,\,\,\frac{(n-1)}{\sum\limits_j \frac{\chi_{j}} {\omega_{j}}} $$

(25)

Note that $e_{r}^{\ast } >e_{s}^{\ast } \,\,\text {if}\,\,\frac {\chi _{s}} {\omega _{s}} >\frac {\chi _{r}} {\omega _{r}}$.

We can also compute equilibrium probabilities in this case to be as follows:

$$ P_{i}^{\ast} = 1-\frac{(n-\bar{{n}})\frac{\chi_{i}} {\omega_{i}} }{\sum\limits_j{\frac{\chi_{j}} {\omega_{j}} }}. $$

(26)

Notice that lower is the cost of exerting effort, $\frac {\chi _{i}} {\omega _{i}}$, relative to $\sum \limits _j {\frac {\chi _{j}} {\omega _{j}} }$, the higher is the probability of finding a seat (please refer to footnote 11 in the paper for an interpretation of heterogeneity of cost functions in our context).

Moreover, note that if all costs of effort $\left ({\chi _{i}} \right )$ are multiplied by $\tau$, then each level of effort is divided by $\tau$, and the total cost of effort $\sum \limits _j {\chi _{j} e_{j}}$ (for this case of α_i = 0) remains the same. Taking effort multiplicatively has no impact of consumers’ surplus, so that the tax revenue $(\tau -1)\,\sum \limits _j {e_{j}}$ corresponds to the social benefit.

We can verify that in the symmetric case, we have:

$$e^{\ast} =\left( {1-\frac{(n-1)}{n}} \right)\,\,\,\frac{(n-1)\,\omega} {n\,\chi} $$

$$e^{\ast} =\frac{\omega} {\chi} \,\,\left( {\frac{n-1}{n^{2}}} \right)\,\,\,=\frac{\left[ {g\,(n-\bar{{n}})\,-\bar{{c}}} \right]}{\chi} \,\,\left( {\frac{n-\bar{{n}}}{n^{2}}} \right) $$

as derived earlier.

Appendix D: Proof of Propsition 6

Proof

The planner minimizes the following objective function w.r.t. $\,\bar {{n}}$:

$$\sum\limits_{i = 1}^n {C_{i}} +\pi \,\bar{{n}}=\bar{{n}}\,\bar{{c}}+\frac{(n-\bar{{n}})^{2}}{S-J\bar{{n}}}+\frac{(n-\bar{{n}})}{n\,(\alpha + 1)}\,\,\left[ {\frac{n-\bar{{n}}}{S-J\bar{{n}}}\,-\bar{{c}}} \right]\,\,+\pi \,\bar{{n}}. $$

Differentiatingw.r.t. $\bar {{n}}$,the F.O.C. is:

$$(\pi +\bar{{c}})\,(S-J\bar{{n}})^{2}\,\,-2\,(n-\bar{{n}})\,\,(S-J\bar{{n}})+(n-\bar{{n}})^{2}J $$

$$-\frac{(S-J\bar{{n}})}{n\,(\alpha + 1)}\,\,(n-\bar{{n}}-\bar{{c}}(S-J\bar{{n}}))\,+\frac{(n-\bar{{n}})\,\,(Jn-S)}{n\,(\alpha + 1)}= 0. $$

This is a quadratic equation in$\bar {{n}}$ and can be written inthe form $A\bar {{n}}^{2}+B\bar {{n}}+C = 0$ where thecoefficients are as follows:

$$A=-J\,\,\left[ {-J\,(\pi +\bar{{c}})+ 1+\frac{1-J\bar{{c}}}{n\,(\alpha + 1)}} \right] $$

$$B = 2S\,\left[ {-J\,(\pi +\bar{{c}})+ 1+\frac{1-J\bar{{c}}}{n\,(\alpha + 1)}} \right] $$

$$C=(\pi +\bar{{c}})\,S^{2}-2nS+Jn^{2}-\frac{2S}{\alpha + 1}+\frac{\bar{{c}}S^{2}}{n\,(\alpha + 1)}+\frac{Jn}{\alpha + 1}. $$

In general, it is difficult to get a closed-form solution to the above equation. Hence we let n and S be large (as isplausible), so that we get the following approximations:

$$A=-J\,[-J\,(\pi +\bar{{c}})+ 1\,] $$

$$B = 2S\,[-J\,(\pi +\bar{{c}})+ 1\,] $$

$$C=(\pi +\bar{{c}})\,S^{2}-2nS+Jn^{2}. $$

Now substituting in the equation and solving, we get

$$(S-J\bar{{n}})\,^{2}(J\,(\pi +\bar{{c}})\,-1)\,+(S^{2}-Jn)^{2}= 0. $$

So for any feasible solution, wemust have $J\,(\pi +\bar {{c}})<1$. (This is plausiblegiven that $\pi ,\,\bar {{c}}$ andJ are likely to be small and can be chosen appropriately). Hence we can solve$\bar {{n}}^{\ast }$ from above tobe:

$$\bar{{n}}^{\ast} =\frac{S}{J}-\left( {n-\frac{S}{J}} \right)\,\frac{1}{\sqrt {1-J(\pi +\bar{{c}})}} . $$

(Notice that$Jn>S$, otherwise$\bar {{n}}=n$ andthe problem of congestion would not be relevant.) We can check that the S.O.C. for minimizationalso holds.

However, notice that if n is very large, then$\bar {{n}}^{\ast }$ will become negative,so that the optimal $\bar {{n}}$ will be 0. Hence we can solve for the cut-off of n for feasible$\bar {{n}}$, bysetting

$$\frac{S}{J}-\left( {n-\frac{S}{J}} \right)\,\frac{1}{\sqrt {1-J(\pi +\bar{{c}})}} = 0. $$

This solves for

$$ n=\frac{S}{J}\left( {\sqrt {1-J(\pi +\bar{{c}})} + 1} \right). $$

(27)

Call n in Eq. 27, $\underline {n}.$ Hence

$$ \bar{{n}}^{\ast} =\left\{\begin{array}{ll} {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \hfill & {\text{if}\,\,n\ge \underline{n};} \hfill \\ \frac{S}{J}-\left( {n-\frac{S}{J}} \right)\frac{1}{\sqrt {1-J(\pi +\bar{{c}})}} >0 \hfill & {\text{if}\,\,n<\underline{n}.} \hfill \end{array}\right. $$

(28)

□

Appendix E: Proof of Proposition 7

Proof

Differentiating $\bar {{n}}^{\ast }$ we get the following.

$$\frac{\partial \bar{{n}}^{\ast} }{\partial \pi} =-\left( {n-\frac{S}{J}} \right)\,\left( {-\frac{1}{\left( {\sqrt {1-J(\pi +\bar{{c}})}} \right)^{2}}} \right)\,(-J)<0, $$

$$\frac{\partial \bar{{n}}^{\ast} }{\partial n}=-\frac{1}{\sqrt {1-J(\pi +\bar{{c}})}} <0, $$

$$\frac{\partial \bar{{n}}^{\ast} }{\partial \bar{{c}}}=-\left( {n-\frac{S}{J}} \right)\,\left( {-\frac{1}{\left( {\sqrt {1-J(\pi +\bar{{c}})}} \right)^{2}}} \right)(-J)<0, $$

$$\frac{\partial \bar{{n}}^{\ast} }{\partial J}=-\frac{S}{J^{2}}-\left[ {\frac{S}{J^{2}}\,\,\frac{1}{\sqrt {1-J(\pi +\bar{{c}})}} +\left( {n-\frac{S}{J}} \right)\,\left( {-\frac{1}{\left( {\sqrt {1-J(\pi +\bar{{c}})}} \right)^{2}}} \right)\,\,(-(\pi +\bar{{c}}))} \right] $$

< 0,

$$\frac{\partial \bar{{n}}^{\ast} }{\partial S}=\frac{1}{J}+\frac{1}{J}\sqrt {1-J(\pi +\bar{{c}})} \,\,>0. $$

This proves theproposition. □

Appendix F: Proof of Propsition Lemma 2: Derivation Of $\kappa$

Proof

Summing over all possible outcomes, we get

$$1=\sum\limits_{\bar{{\upsilon} }\in {\Omega}} p_{\bar{{\upsilon} }} =\kappa \times \left\{ {\sum\limits_{\bar{{\upsilon} }\in {\Omega}} \sum\limits_{{\begin{array}{*{20}c} {\bar{{\upsilon} }\in {\Omega}} \hfill \\ {\varepsilon_{i} (\bar{{\upsilon} })= 0} \hfill \end{array}} } e_{il} +\sum\limits_{\bar{{\upsilon} }\in {\Omega}} \sum\limits_{{\begin{array}{*{20}c} {\bar{{\upsilon} }\in {\Omega}} \hfill \\ {\varepsilon_{i} (\bar{{\upsilon} })= 1} \hfill \end{array}} } e_{ih}} \right\}. $$

$$1=\kappa \times \left\{ {\sum\limits_i{e_{il}} \left( {\sum\limits_{{\begin{array}{*{20}c} {\bar{{\upsilon} }\in {\Omega}} \hfill \\ {\varepsilon_{i} (\bar{{\upsilon} })= 0} \hfill \end{array}} }1} \right)+\sum\limits_i {e_{ih}} \left( {\sum\limits_{{\begin{array}{*{20}c} {\bar{{\upsilon} }\in {\Omega}} \hfill \\ {\varepsilon_{i} (\bar{{\upsilon} })= 1} \hfill \end{array}} }1} \right)} \right\}. $$

(There is no effortcounted for $\varepsilon _{i} =-1.)\,$Now$\left ({\sum \nolimits _{{\begin {array}{*{20}c} {\bar {{\upsilon } }\in {\Omega }} \hfill \\ {\varepsilon _{i} (\bar {{\upsilon } })= 0} \hfill \end {array}} } 1} \right )$ counts the number ofvectors of length $\left ({n-1} \right )$ (sincethe i th person’s outcome is known which is to get the low quality goods), where there are$\bar {{n}}$ number of 1’s(since $\bar {{n}}$ peopleare getting the higher quality good), and the rest can have any two possible outcomes,$\varepsilon = 0,\,-1$, that isthey may have got the lower quality goods, or may not have got any goods at all. Hence we get thefollowing:

$$\sum\limits_{{\begin{array}{*{20}c} {\bar{{\upsilon} }\in {\Omega}} \hfill \\ {\varepsilon_{i} (\bar{{\upsilon} })= 0} \hfill \end{array}} } 1 =\left( {{\begin{array}{*{20}c} {n-1} \hfill \\ {\bar{{n}}} \hfill \end{array}} } \right)\,\,\times \,\,2^{(n-1-\bar{{n}})}. $$

Similarly,$\left ({\sum \nolimits _{{\begin {array}{*{20}c} {\bar {{\upsilon } }\in {\Omega }} \hfill \\ {\varepsilon _{i} (\bar {{\upsilon } })= 1} \hfill \end {array}} } 1} \right )$ counts the number ofvectors of length $\left ({n-1} \right )$ with$\left ({\bar {{n}}-1} \right )$ numberof 1’s (since the i th person has got the higher quality good), and is givenby

$$\sum\limits_{{\begin{array}{*{20}c} {\bar{{\upsilon} }\in {\Omega}} \hfill \\ {\varepsilon_{i} (\bar{{\upsilon} })= 1} \hfill \end{array}} } 1 =\left( {{\begin{array}{*{20}c} {n-1} \hfill \\ {\bar{{n}}-1} \hfill \end{array}} } \right)\,\,\times \,\,2^{(n-1)\,-(\bar{{n}}-1)}=\left( {{\begin{array}{*{20}c} {n-1} \hfill \\ {\bar{{n}}-1} \hfill \end{array}} } \right)\,\,\times \,\,2^{(n-\bar{{n}})}. $$

Substituting these in theabove expression, and letting $\sum \nolimits _i {e_{ih}} =e_{H}$,and $\sum \nolimits _i {e_{il}} =e_{L}$ we cansolve $\kappa$ asfollowing:

$$\kappa =\frac{1}{\left( {{\begin{array}{*{20}c} n \hfill \\ {\bar{{n}}} \hfill \end{array}} } \right)\,2\,^{(n-\bar{{n}}-1)}\left\{ {e_{L} \,\left( {\frac{n-\bar{{n}}}{n}} \right)+ 2\frac{\bar{{n}}}{n}\,e_{H}} \right\}}. $$

□

Appendix G: Correlation

Let us see the correlation between the outcomes of two individuals, that is, say we are interested in the correlation of the outcomes players 1 and 2, Corr(ε₁,ε₂). Now

$$Corr\,\left( {\varepsilon_{1} ,\varepsilon_{2}} \right)=\frac{Cov\,\left( {\varepsilon_{1} ,\varepsilon_{2}} \right)}{\sqrt {Var\,\left( {\varepsilon_{1}} \right)Var\,\,\left( {\varepsilon_{2}} \right)}} $$

$$= \quad E\,(\varepsilon_{1} \varepsilon_{2} )\,-E(\varepsilon_{1} )\,E(\varepsilon_{2} ). $$

We know (from calculations before) that $E\,(\varepsilon _{1} )=\Pr \,\{\varepsilon _{1} \}= 1$. Similarly, $E\,(\varepsilon _{2} )=\Pr \,\{\varepsilon _{2} \}= 1.$Also, $E\,(\varepsilon _{1} \varepsilon _{2} )=\Pr \,\{\varepsilon _{1} \varepsilon _{2} \}= 1$ (since in all other possibilities, $\varepsilon _{1}$or $\varepsilon _{2}$or both are 0 and there is no contribution to the expectation). Now (restricting to the $\lambda =$ 0 case), we have

$$\Pr \,\left\{ {\varepsilon_{1} = 1,\,\varepsilon_{2} = 1} \right\}=\sum\limits_{\begin{array}{l} {\begin{array}{*{20}c} {v\in {\Omega}} \hfill \\ {\varepsilon_{1} (v)= 1} \hfill \end{array}} \\ \varepsilon_{2} (v)= 1 \end{array}} {p_{v}} $$

$$=\sum\limits_{\begin{array}{l} {\begin{array}{*{20}c} {v\in {\Omega}} \hfill \\ {\varepsilon_{1} (v)= 1} \hfill \end{array}} \\ \varepsilon_{2} (v)= 1 \end{array}} K \left[ {\sum\limits_{i = 1}^n {\varepsilon_{i} (v)\,e_{i}}} \right] $$

(where K is as given in Eq. 4 with $\lambda = 0)$

$$=K\left[ {\sum\limits_{i = 1}^n {\,e_{i}} \,\,\,\,\,\sum\limits_{\begin{array}{l} {\begin{array}{*{20}c} {v\in {\Omega}} \hfill \\ {\varepsilon_{1} (v)= 1} \hfill \end{array}} \\ \varepsilon_{2} (v)= 1 \end{array}}{\varepsilon_{i} (v)} \,\,\,\,\,} \right] $$

$$=K\left[ {\sum\limits_{i = 1}^n {\,e_{i}} \sum\limits_{\begin{array}{l} {\begin{array}{*{20}c} {v\in {\Omega}} \hfill \\ {\varepsilon_{1} (v)= 1} \hfill \end{array}} \\ \varepsilon_{2} (v)= 1 \\ \varepsilon_{i} (v)= 1 \end{array}} 1 \,\,\,\,\,} \right]. $$

_Now

$$\sum\limits_{\begin{array}{l} {\begin{array}{*{20}c} {\mathbf{v}\in {\Omega}} \hfill \\ {\varepsilon_{1} (\mathbf{v})= 1} \hfill \end{array}} \\ \varepsilon_{2} (\mathbf{v})= 1 \end{array}} 1 =\left\{ {{\begin{array}{*{20}c} {\left( {\begin{array}{l} n-2 \\ \bar{{n}}-2 \end{array}} \right)} \hfill \\ {\left( {\begin{array}{l} n-2 \\ \bar{{n}}-2 \end{array}} \right)} \hfill \\ {\left( {\begin{array}{l} n-3 \\ \bar{{n}}-3 \end{array}} \right)} \hfill \end{array}} {\begin{array}{*{20}c} {\begin{array}{l} \,\,\,\,\text{if}\,\,i = 1 \\ \end{array}} \hfill \\ {\text{if}\,\,i = 2} \hfill \\ {\begin{array}{l} \\ \text{if}\,\,i\ne 1,\,2 \end{array}} \hfill \end{array}} } \right.. $$

Substituting and simplifying, we get

$$\Pr \,\left\{ {\varepsilon_{1} = 1,\varepsilon_{2} = 1\,} \right\}=\frac{\left( {\bar{{n}}-1} \right)\,(\bar{{n}}-2)}{(n-1)\,(n-2)}+\frac{(e_{1} +e_{2} )}{\sum\nolimits_i e_{i}} \frac{\left( {n-\bar{{n}}} \right)(\bar{{n}}-1)}{(n-1)\,(n-2)}. $$

Recall that

$$\Pr \,\left\{ {\varepsilon_{i} = 1\,} \right\}=\frac{\bar{{n}}-1}{n-1}+\frac{e_{i}} {\sum\nolimits_i {e_{i}} } \frac{n-\bar{{n}}}{n-1\,}. $$

Hence we get

$$Cov(\varepsilon_{1} ,\varepsilon_{2} )=\frac{\left( {\bar{{n}}-1} \right)\,(\bar{{n}}-2)}{(n-1)\,(n-2)}+\frac{(e_{1} +e_{2} )}{\sum\nolimits_i e_{i}} \frac{\left( {n-\bar{{n}}} \right)(\bar{{n}}-1)}{(n-1)\,(n-2)} $$

$$-\left[ {\frac{\bar{{n}}-1}{n-1}+\frac{e_{1}} {\sum\nolimits_i{e_{i}} } \frac{n-\bar{{n}}}{n-1\,}} \right]\,\,\left[ {\frac{\bar{{n}}-1}{n-1}+\frac{e_{2}} {\sum\nolimits_i {e_{i}}} \frac{n-\bar{{n}}}{n-1\,}} \right]. $$

Also we can calculate that

$$Var\,\left( {\varepsilon_{1}} \right)=(\Pr \,\{\varepsilon_{1} = 1\})\,\,(1-\Pr \,\{\varepsilon_{1} = 1\}). $$

Now by substituting all the expressions we can get $Corr\,\left ({\varepsilon _{1} ,\varepsilon _{2}} \right )$. Now, in order to keep the calculations tractable, we make the simplifying assumption of letting n being large (so that $\frac {1}{n}\approx 0$). In this case, dividing the expression for $Cov\,\left ({\varepsilon _{1} ,\varepsilon _{2}} \right )$ throughout by n and letting $\frac {1}{n}\approx 0$, we get

$$Cov(\varepsilon_{1} ,\varepsilon_{2} )=\frac{\bar{{n}}^{2}}{n}+\frac{(e_{1} +e_{2} )}{\sum\nolimits_i{e_{i}} }\,\frac{\bar{{n}}}{n}\,\,\,\left( {1-\frac{\bar{{n}}}{n}} \right) $$

$$-\left[ {\frac{\bar{{n}}}{n}+\frac{e_{1}} {\sum\nolimits_i {e_{i}} } \left( {1-\frac{\bar{{n}}}{n}} \right)} \right]\,\,\left[ {\frac{\bar{{n}}}{n}+\frac{e_{2}} {\sum\nolimits_i {e_{i}} } \left( {1-\frac{\bar{{n}}}{n}} \right)} \right]. $$

Simplifying the above expression we get

$$Cov(\varepsilon_{1} ,\varepsilon_{2} )=-\frac{(e_{1} e_{2} )}{\left( {\sum\nolimits_i{e_{i}} } \right)^{2}}\,\,\,\left( {1-\frac{\bar{{n}}}{n}} \right)^{2}<0. $$

Hence $Corr\,\left ({\varepsilon _{1} ,\varepsilon _{2}} \right )<0$. In fact, we can calculate the expression for $Corr\,\left ({\varepsilon _{1} ,\varepsilon _{2}} \right )$ more precisely in this case. Notice that when n is large

$$\Pr \{\varepsilon_{1} = 1\}=\frac{\bar{{n}}}{n}+\frac{e_{1} }{\sum\nolimits_i {e_{i}} } \,\left( {1-\frac{\bar{{n}}}{n}} \right). $$

And variance can be calculated as

$$Var\,(\varepsilon_{1} )=\left( {\frac{\bar{{n}}}{n}+\,\frac{e_{1}} {\sum\nolimits_i {e_{i}} } \,\left( {1-\frac{\bar{{n}}}{n}} \right)} \right)\,\,\left( {1-\frac{\bar{{n}}}{n}} \right)\,\,\left( {1-\frac{e_{1}} {\sum\nolimits_i {e_{i}} } } \right). $$

Hence substituting and simplifying, we get the expression for the correlation coefficient as below:

$$Corr\,\,(\varepsilon_{1} ,\varepsilon_{2} )=-\frac{\frac{e_{1} \,e_{2}} {\left( {\sum\nolimits_i {e_{i}} } \right)^{2}}}{\sqrt {\left( {\frac{\bar{{n}}}{n}+\frac{e_{1}} {\sum\nolimits_i {e_{i}} } \left( {1-\frac{\bar{{n}}}{n}} \right)} \right)\,\left( {1-\frac{e_{1}} {\sum\nolimits_i {e_{i}} } } \right)\,\left( {\frac{\bar{{n}}}{n}+\frac{e_{2}} {\sum\nolimits_i {e_{i}} } \left( {1-\frac{\bar{{n}}}{n}} \right)} \right)\,\,\,\left( {1-\frac{e_{2}} {\sum\nolimits_i {e_{i}} } } \right)} \,\,\,\,}<0 $$

Notice that the correlation coefficient is generalizable to that between outcomes of any two individuals i andj after appropriately substituting for 1 and 2 in the expression on the R.H.S. Hence we see that, as expected, the correlation between outcomes of any two individuals is negative, that is, as one person’s chances of getting a better-quality good increases, that of the other falls. The following proposition summarizes the findings.

Proposition 2

The correlation coefficient between the outcomes of any two individuals, sayindividualiandindividual$j, \quad i\ne j,$,is given as

$$Corr\,\,(\varepsilon_{i} ,\varepsilon_{j} )=-\frac{\frac{e_{i} \,e_{j}} {\left( {\sum\nolimits_i {e_{i}} } \right)^{2}}}{\sqrt {\left( {\frac{\bar{{n}}}{n}+\frac{e_{i}} {\sum\nolimits_i {e_{i}} } \left( {1-\frac{\bar{{n}}}{n}} \right)} \right)\,\left( {1-\frac{e_{i}} {\sum\nolimits_i {e_{i}} } } \right)\,\left( {\frac{\bar{{n}}}{n}+\frac{e_{j}} {\sum\nolimits_i {e_{i}} } \left( {1-\frac{\bar{{n}}}{n}} \right)} \right)\,\,\,\left( {1-\frac{e_{j}} {\sum\nolimits_i {e_{i}} } } \right)} \,\,\,\,} $$

$$=\frac{-\frac{e_{i} e_{j}} {\bar{{e}}^{2}}}{\sqrt {\,\left( {\bar{{n}}+\frac{e_{i}} {\bar{{e}}}\left( {1-\frac{\bar{{n}}}{n}} \right)\,} \right)\,\left( {n-\frac{e_{i}} {\bar{{e}}}} \right)\,\left( {\bar{{n}}+\frac{e_{j}} {\bar{{e}}}\left( {1-\frac{\bar{{n}}}{n}} \right)\,} \right)\,\,\left( {n-\frac{e_{j}} {\bar{{e}}}} \right)} \,\,\,\,\,\,}<0. $$

Moreover, in case the number of better quality goods is small relative to the total number of consumers, so that$\frac {\bar {{n}}}{n}\approx 0$, wecan further simplify the expression of correlation coefficient to arrive at the following corollary.

Corollary 1

If $\frac {\bar {{n}}}{n}\approx 0$ then we get

$$Corr\,\,(\varepsilon_{i} ,\varepsilon_{j} )=-\sqrt {\frac{e_{i} e_{j}} {(\sum\nolimits_i {e_{i}} -e_{i} )\,\,\,\left( {\sum\nolimits_i e_{i} -e_{j}} \right)}.} $$

Appendix H: Lottery

Consider a situation in which each person can buy more than one ticket for a limited number of prizes. Say there are k number of people, $n$ the total number of tickets for $\bar {{n}}$ number of prizes (seats), with $n>\bar {{n}}$. Let $e_{i}$ be the number of tickets purchased by player $i$ (note this has nothing to do with effort as of now). Assume all available tickets are bought, that is $\sum \nolimits _{i = 1}^k {e_{i}} =n_{\mathrm { } }$ and also $e_{i} \,\in \,\left \{ {1,\,2,\mathellipsis ,n-k + 1} \right \}$. Hence the space of all outcomes ${\Omega }$, is as follows:

$${\Omega} :\!\left\{ {v=(\varepsilon_{11} (\textbf{v}),\mathellipsis ,\varepsilon_{1e_{1}} (\textbf{v}),\varepsilon_{21} (\textbf{v}),\mathellipsis ,\varepsilon_{2e_{2}} (\textbf{v}),...,\varepsilon_{k1} (\textbf{v})\,\mathellipsis ,\varepsilon_{ke_{k}} (\textbf{v}))\,\in \left\{ {0,1} \right\}^{n}:\!\sum\limits_{i = 1}^k {\sum\limits_{j = 1}^{e_{i}} {\varepsilon_{ij}} } (\textbf{v})=\bar{{n}}} \right\} $$

where $\varepsilon _{ke_{k}} (\textbf {v})$ is the n-th component of the vector v.

The restriction $\sum \limits _{i = 1}^k {\sum \limits _{j = 1}^{e_{i}} {\varepsilon _{ij} (\mathbf {v})} =\bar {{n}}}_{\mathrm { } }$ reflects the fact that in any outcome, all the prizes are won. Moreover, the first $e_{1}$ outcomes in v reflect the outcomes for the tickets bought by player 1. Note that here $\varepsilon _{ij} (\text {v})= 1$ means that in the outcome v the i-th person has won in the j th ticket and otherwise $\varepsilon _{ij} (\text {v})= 0$. Also note that the number of outcomes in the space is given by

$$\left| {\Omega \,} \right|=\left( {\begin{array}{l} n \\ \bar{{n}} \end{array}} \right)=\frac{n!}{\bar{{n}}!\,(n-\bar{{n}})!}. $$

Now let us compute the probability that any person, say person 1, has won p prizes (where $p\le e_{1}$, that is number of prizes won is less than the number of tickets bought by person 1 and $p\le \bar {{n}}$, that is the number of prizes won is less than the total number of prizes). Now all outcomes are equally likely. Moreover person 1 wins p prizes with $e_{1}$ number of tickets in $\left ({\begin {array}{l} e_{1} \\ p \end {array}} \right )$ ways. For each way, the rest $\bar {{n}}-p$ prizes can be won by $n-e_{1}$ tickets in $\left ({\begin {array}{l} n-e_{1} \\ \bar {{n}}-p \end {array}} \right )$. Hence the probability is given by:

Pr{Player 1 wins p prizes}$={\begin {array}{*{20}c} {\sum \limits _{v\in {\Omega }}} \hfill \\ {\varepsilon _{11} (v)+\mathellipsis \varepsilon _{1e_{1}} (v)=p} \hfill \par \end {array}} \frac {1}{\left ({\begin {array}{l} n \\ \bar {{n}} \end {array}} \right )}\,\,$

$$=\frac{\left( {\begin{array}{l} e_{1} \\ p\,\, \end{array}} \right)\,\,\,\left( {\begin{array}{l} n-e_{1} \\ \bar{{n}}-p \end{array}} \right)}{\left( {\begin{array}{l} n \\ \bar{{n}} \end{array}} \right)}. $$

More generally, the probability that the $l-$th player will win p prizes is given by

Pr {Player $\ell$ wins p prizes}$=\frac {\left ({\begin {array}{l} e_{l} \\ p\,\, \end {array}} \right )\,\,\,\left ({\begin {array}{l} n-e_{l} \\ \bar {{n}}-p \end {array}} \right )}{\left ({\begin {array}{l} n \\ \bar {{n}} \end {array}} \right )}.$

Now our model can be related to this lottery set-up in the following way: let each ticket, for example, to be a unit of effort exerted, so that more number of tickets will correspond to more effort exerted (of course, effort in our model is a continuous variable while number of tickets can only be discrete). If tickets have a (uniform) price, that might be interpreted as $\chi$ in our model. Hence the total expenditure, of person i, to purchase $e_{i}$ number of tickets, would be $\chi e_{i}$, the total ‘effort cost’ of player i in our model (assuming $\alpha = 0$, or linear cost of effort).

Interestingly, in the (usual) case with every person buying only one ticket $e_{i} = 1,\,\,\forall {i}$ (or alternatively the symmetric effort case with everybody exerting the same effort), the probability that the ith person wins is given by

Pr {Player i wins p prizes}$~=~\frac {\left ({\begin {array}{l} 1 \\ 1\,\, \end {array}} \right )\,\,\,\left ({\begin {array}{l} n-1 \\ \bar {{n}}-1 \end {array}} \right )}{\left ({\begin {array}{l} n \\ \bar {{n}} \end {array}} \right )}=\frac {\bar {{n}}}{n}$,

which is the usual random probability model that we had.