Abstract
This note provides an extension of the constructive loop vertex expansion to stable interactions of arbitrarily high order, opening the way to many applications. We treat in detail the example of the \((\bar{\phi } \phi )^p\) field theory in zero dimension. We find that the important feature to extend the loop vertex expansion is not to use an intermediate field representation, but rather to force integration of exactly one particular field per vertex of the initial action.


Similar content being viewed by others
Notes
Here it is fair to add that the models built so far are only of the superrenormalizable type. Moreover, the MLVE is especially adapted to resum the renormalized series of non-local field theories of the matrix or tensorial type. For ordinary local field theories, until now, and in contrast with the more traditional constructive methods such as cluster and Mayer expansions, it does not conveniently provide the spatial decay of truncated functions. See, however, [18, 19].
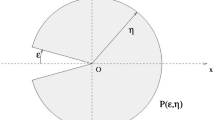
This terminology follows from the graphical representation of \(S_p\) given in Sect. 4.
We thank A. Sokal for pointing this argument to us.
References
Rivasseau, V.: Constructive matrix theory. JHEP 0709, 008 (2007). arXiv:0706.1224 [hep-th]
Brydges, D., Kennedy, T.: Mayer expansions and the Hamilton–Jacobi equation. J. Stat. Phys. 48, 19 (1987)
Abdesselam, A., Rivasseau, V.: Trees, forests and jungles: a botanical garden for cluster expansions. In: Constructive Physics, Lectures Notes in Physics, vol. 446. Springer, New York (1995). arXiv:9409094 [hep-th]
Rivasseau, V., Wang, Z.: How to resum Feynman graphs. Annales Henri Poincaré 15(11), 2069 (2014). arXiv:1304.5913 [math-ph]
Gurau, R., Ryan, J.P.: Colored tensor models—a review. SIGMA 8, 020 (2012). arXiv:1109.4812 [hep-th]
Gurau, R.: Random Tensors. Oxford University Press, Oxford (2016)
’t Hooft, G.: A planar diagram theory for strong interactions. Nucl. Phys. B 72, 461 (1974)
Gurau, R.: The \(1/N\) expansion of colored tensor models. Annales Henri Poincaré 12, 829 (2011). arXiv:1011.2726 [gr-qc]
Gurau, R., Rivasseau, V.: The \(1/N\) expansion of colored tensor models in arbitrary dimension. Europhys. Lett. 95, 50004 (2011). arXiv:1101.4182 [gr-qc]
Gurau, R.: The complete \(1/N\) expansion of colored tensor models in arbitrary dimension. Annales Henri Poincaré 13, 399 (2012). arXiv:1102.5759 [gr-qc]
Gurau, R., Krajewski, T.: Analyticity results for the cumulants in a random matrix model. Ann. Inst. H. Poincaré D, Comb. Phys. Interact. 2, 169–228 (2015). arXiv:1409.1705 [math-ph]
Gurau, R.: The \(1/N\) expansion of tensor models beyond perturbation theory. Commun. Math. Phys. 330, 973 (2014). arXiv:1304.2666 [math-ph]
Delepouve, T., Gurau, R., Rivasseau, V.: Universality and Borel summability of arbitrary quartic tensor models. Ann. Inst. H. Poincaré Probab. Stat. 52(2), 821–848 (2016). arXiv:1403.0170 [hep-th]
Gurau, R., Rivasseau, V.: The multiscale loop vertex expansion. Annales Henri Poincaré 16(8), 1869 (2015). arXiv:1312.7226 [math-ph]
Delepouve, T., Rivasseau, V.: Constructive tensor field theory: the \(T^4_3\) model. Commun. Math. Phys. 345, 477–506 (2016). arXiv:1412.5091 [math-ph]
Lahoche, V.: Constructive Tensorial Group Field Theory II: The \(U(1)-T^4_4\) Model. arXiv:1510.05051 [hep-th]
Rivasseau, V., Vignes-Tourneret, F.: Constructive tensor field theory: the \(T^{4}_{4}\) model. arXiv:1703.06510 [math-ph]
Magnen, J., Rivasseau, V.: Constructive \(\phi ^4\) field theory without tears. Annales Henri Poincaré 9, 403 (2008). arXiv:0706.2457 [math-ph]
Rivasseau, V., Wang, Z.: Corrected loop vertex expansion for \(\Phi _2^4\) theory. J. Math. Phys. 56(6), 062301 (2015). arXiv:1406.7428 [math-ph]
Rivasseau, V., Wang, Z.: Loop vertex expansion for Phi**2K theory in zero dimension. J. Math. Phys. 51, 092304 (2010). arXiv:1003.1037 [math-ph]
Lionni, L., Rivasseau, V.: Note on the Intermediate Field Representation of \(\phi ^{2k}\) Theory in Zero Dimension. arXiv:1601.02805
Lionni, L., Rivasseau, V.: Intermediate Field Representation for Positive Matrix and Tensor Interactions. arXiv:1609.05018 [math-ph]
Gallavotti, G.: Perturbation theory. In: Sen, R., Gersten, A. (eds.) Mathematical Physics Towards the XXI Century, pp. 275–294. Ben Gurion University Press, Ber Sheva (1994)
Młotkowski, W., Penson, K.A.: Probability distributions with binomial moments. Infin. Dimens. Anal. Quantum. Probab. Relat. Top. 17, 1450014 (2014)
Bonzom, V., Gurau, R., Riello, A., Rivasseau, V.: Critical behavior of colored tensor models in the large N limit. Nucl. Phys. B 853, 174 (2011). arXiv:1105.3122 [hep-th]
Rivasseau, V.: Quantum gravity and renormalization: the tensor track. AIP Conf. Proc. 1444, 18–29 (2012). arXiv:1112.5104
Rivasseau, V.: The Tensor Track: An Update. Symmetries and Groups in Contemporary Physics, pp. 63–74, World Scientific, Singapore (2013). arXiv:1209.5284
Rivasseau, V.: The tensor track, III. Fortsch. Phys. 62, 81 (2014). arXiv:1311.1461 [hep-th]
Rivasseau, V.: The tensor track, IV. PoS CORFU 2015, 106 (2016). arXiv:1604.07860 [hep-th]
Rivasseau, V.: Random tensors and quantum gravity. SIGMA 12, 069 (2016). arXiv:1603.07278 [math-ph]
Witten, E.: An SYK-Like Model Without Disorder. arXiv:1610.09758 [hep-th]
Gurau, R.: The complete \(1/N\) expansion of a SYK-like tensor model. Nucl. Phys. B 916, 386 (2017). arXiv:1611.04032 [hep-th]
Klebanov, I.R., Tarnopolsky, G.: Uncolored random tensors, melon diagrams, and the SYK models. Phys. Rev. D 95(4), 046004 (2017). arXiv:1611.08915 [hep-th]
Krishnan, C., Sanyal, S., Bala Subramanian, P.N.: Quantum chaos and holographic tensor models. J. High Energy Phys. 56, (2017). arXiv:1612.06330 [hep-th]
Ferrari, F.: The Large D Limit of Planar Diagrams. To Appear in Ann. Inst. H. Poincaré D. arXiv:1701.01171 [hep-th]
Gurau, R.: Quenched equals annealed at leading order in the colored SYK model. arXiv:1702.04228 [hep-th]
Bonzom, V., Lionni, L., Tanasa, A.: Diagrammatics of a colored SYK model and of an SYK-like tensor model, leading and next-to-leading orders. J. Math. Phys. 58, 052301 (2017). arXiv:1702.06944 [hep-th]
Ben Geloun, V., Rivasseau, V.: A renormalizable 4-dimensional tensor field theory. Commun. Math. Phys. 318, 69 (2013). arXiv:1111.4997 [hep-th]
Carrozza, S., Oriti, D., Rivasseau, V.: Renormalization of a SU(2) tensorial group field theory in three dimensions. Commun. Math. Phys. 330, 581 (2014). arXiv:1303.6772 [hep-th]
Perrin, D.: Private communication
Osada, H.: The Galois group of the polynomials \(X^n + a X^{\prime } +b\). J. Number Theory 25, 230–238 (1987)
Rivasseau, V.: Constructive tensor field theory. SIGMA 12, 085 (2016). arXiv:1603.07312 [math-ph]
Acknowledgements
We thank G. Duchamp, R. Gurau, L. Lionni and A. Sokal for useful discussions.
Author information
Authors and Affiliations
Corresponding author
Appendix: explicit formulas for p small
Appendix: explicit formulas for p small
1.1 The \((\bar{\phi } \phi )^2\) theory
In this case, \(g= (-\lambda )^{\frac{1}{2}} = i \sqrt{\lambda }\), \(\lambda = - g^2\) and \(z = g^2 \bar{\phi } \phi = - \lambda \bar{\phi } \phi \). Equation (2.14) takes the form
with solution the ordinary Catalan function
We find
and the LVR action is
Its first-order derivative is
so that the loop vertex representation of the partition function is
We recover the familiar logarithmic form of the action and resolvent of the intermediate field theory. However, our LVR representation is not the intermediate field representation. Indeed, in the LVR representation the argument of the log is quadratic in complex fields similar to the initial fields although it would be linear in the single real field \(\sigma \) of the intermediate field representation. We should rather think to the fields of the LVR as what remains of the initial fields after having forced integration of one particular marked \(\bar{\phi }\) field per vertex.
1.2 The \((\bar{\phi } \phi )^3\) theory
In this case, \(g= (-\lambda )^{\frac{1}{3}} = e^{i\pi /3 } \lambda ^{1/3}\), \(\lambda = - g^3\) and \(z = g^3 (\bar{\phi } \phi )^2 = - \lambda (\bar{\phi } \phi )^2 \). Equation (2.14) is now
which is soluble by radicals. Introducing
Cardano’s solution is
where
Defining \(h (u) := \frac{1}{ \sqrt{1 +u}}\), we can compute the derivatives
Hence
(2.16) gives
The u derivatives of \(S_3\) give access to its g derivatives since \(u= -\frac{27 }{4}g^3 (\bar{\phi } \phi )^2 \), hence
For instance,
We remark that the quotient \(\frac{ \Delta _+ - \Delta _-}{ \Delta _+ + \Delta _-}= \frac{A-B}{A+B}\) for \(A = \Delta _+ \), \(B= \Delta _- \) simplifies, using that \((A+B)(A^2 - AB + B^2) = A^3 + B^3\) and \((A-B)(A^2 - AB + B^2) = A^3 - B^3 -2AB(A-B)\). Remarking that in our case \(AB = \Delta _+ \Delta _-= 1\), we find
from which we find
1.3 The \((\bar{\phi } \phi )^4\) theory
In this case, \(g= (-\lambda )^{\frac{1}{4}} = e^{i\pi /4 } \lambda ^{1/4}\), \(\lambda = - g^4\) and \(z = g^4 (\bar{\phi } \phi )^3 = - \lambda (\bar{\phi } \phi )^3 \). Equation (2.14) is now
which is still soluble by radicals. Denoting
then
We can then compute
from which \(S_4 = \log F_4\) can be derived explicitly.
Rights and permissions
About this article
Cite this article
Rivasseau, V. Loop vertex expansion for higher-order interactions. Lett Math Phys 108, 1147–1162 (2018). https://doi.org/10.1007/s11005-017-1037-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11005-017-1037-9