On deformation of functionally graded narrow beams under transverse loads

Abstract

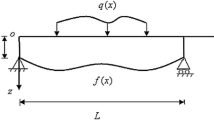
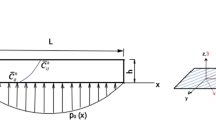
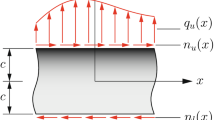
Solution is obtained for functionally graded (FG) narrow beams under plane stress condition of elasticity by using the mixed semi analytical model developed by Kant et al. (Int J Comput Methods Eng Sci Mech 8(3): 165–177, 2007a). The mathematical model consists in defining a two-point boundary value problem (BVP) governed by a set of coupled first-order ordinary differential equations (ODEs) in the beam thickness direction. Analytical solutions based on two dimensional (2D) elasticity, one dimensional (1D) first order shear deformation theory (FOST) and a new 1D higher order shear-normal deformation theory (HOSNT) are also established to show the accuracy, simplicity and effectiveness of the developed mixed semi analytical model. It is observed from the numerical investigation that the present mixed semi analytical model predicts structural response as good as the one given by the elasticity analytical solution which in turn proves the robustness of the present development.

Appendix

The elements of matrix [A] are,

$$ \begin{aligned} [A] & = \int\limits_{o}^{h} {\left[ {\begin{array}{*{20}c} {\,\,\,\,\,C_{11} } & {\,\,z\,C_{11} } & {z^{2} C_{11} } & {z^{3} C_{11} } & {\,\,\,C_{13} } & {\,\,z\,C_{13} } & {z^{2} C_{13} } \\ {\,\,z\,C_{11} } & {z^{2} C_{11} } & {z^{3} C_{11} } & {z^{4} C_{11} } & {\,z\,C_{13} } & {z^{2} C_{13} } & {z^{3} C_{13} } \\ {z^{2} C_{11} } & {z^{3} C_{11} } & {z^{4} C_{11} } & {z^{5} C_{11} } & {z^{2} C_{13} } & {z^{3} C_{13} } & {z^{4} C_{13} } \\ {z^{3} C_{11} } & {z^{4} C_{11} } & {z^{5} C_{11} } & {z^{6} C_{11} } & {z^{3} C_{13} } & {z^{4} C_{13} } & {z^{5} C_{13} } \\ {\,\,\,\,\,C_{13} } & {\,z\,C_{13} } & {z^{2} C_{13} } & {z^{3} C_{13} } & {\,\,\,\,\,C_{33} } & {\,\,z\,C_{33} } & {z^{2} C_{33} } \\ {\,z\,C_{13} } & {z^{2} C_{13} } & {z^{3} C_{13} } & {z^{4} C_{13} } & {\,\,z\,C_{33} } & {z^{2} C_{33} } & {z^{3} C_{33} } \\ {z^{2} C_{13} } & {z^{3} C_{13} } & {z^{4} C_{13} } & {z^{5} C_{13} } & {z^{2} C_{33} } & {z^{3} C_{33} } & {z^{4} C_{33} } \\ \end{array} } \right]\,dz} \\ \;\;\,\,\,\, = A_{ij} (i,\,j = 1\,{\text{ to}}\,{ 7)} \\ \end{aligned} $$

and the coefficients are,

$$ \begin{gathered} A_{11} = {\frac{{\bar{E}_{h} - \bar{E}_{o} }}{\lambda }} \quad A_{12} = {\frac{{h\bar{E}_{h} - A_{11} }}{\lambda }} \quad A_{13} = {\frac{{h^{2} \bar{E}_{h} - 2A_{12} }}{\lambda }} \quad A_{14} = {\frac{{h^{3} \bar{E}_{h} - 3A_{13} }}{\lambda }} \quad \hfill \\ A_{15} = \upsilon A_{11} \quad A_{16} = \upsilon A_{12}\quad A_{17} = \upsilon A_{13} \hfill \\ \quad A_{22} = A_{13} \quad A_{23} = A_{14} \quad A_{24} = {\frac{{h^{4} \bar{E}_{h} - 4A_{23} }}{\lambda }} \quad A_{25} = \upsilon A_{21} \quad \hfill \\ \quad A_{26} = \upsilon A_{22} \quad A_{27} = \upsilon A_{23} \quad \hfill \\ A_{33} = A_{24} \quad A_{34} = {\frac{{h^{5} \bar{E}_{h} - 5A_{33} }}{\lambda }} \quad A_{35} = \upsilon A_{31} \quad A_{36} = \upsilon A_{32} \quad \hfill \\ A_{37} = \upsilon A_{33} \hfill \\ A_{44} = {\frac{{h^{6} \bar{E}_{h} - 6A_{43} }}{\lambda }} \quad A_{45} = \upsilon A_{41} \quad A_{46} = \upsilon A_{42} \quad A_{47} = \upsilon A_{43} \, \hfill \\ A_{55} = A_{11} \quad A_{56} = A_{12} \quad A_{57} = A_{13\,} \hfill \\ A_{66} = A_{22} \quad A_{67} = A_{23} \hfill \\ \quad A_{77} = A_{33} \hfill \\ \end{gathered} $$

where, $\bar{E}_{h} = \left( {{\frac{{E_{o} }}{{1 - \upsilon^{2} }}}} \right)e^{\lambda } {\text{ and }}\bar{E}_{o} = {\frac{{E_{o} }}{{(1 - \upsilon^{2} )}}}$

and A _ij  = A _ji (i, j = 1 to 7)

The elements of matrix [D] are,

$$ \begin{gathered} \left[ D \right] = \int\limits_{o}^{h} {\left[ {\begin{array}{*{20}c} {\,\,C_{44} } & {\,z\,C_{44} } & {z^{2} C_{44} } & {z^{3} C_{44} } \\ {z\,C_{44} } & {z^{2} C_{44} } & {z^{3} C_{44} } & {z^{4} C_{44} } \\ {z^{2} C_{44} } & {z^{3} C_{44} } & {z^{4} C_{44} } & {z^{5} C_{44} } \\ {z^{3} C_{44} } & {z^{4} C_{44} } & {z^{5} C_{44} } & {z^{6} C_{44} } \\ \end{array} } \right]\,dz} \hfill \\ \hfill \\ \,\,\,\,\,\,\,\, = \,D_{ij} \,\, (i,\,j = 1\,{\text{ to}}\, \, 4 )\hfill \\ \end{gathered} $$

and the coefficients are,

$$ \begin{gathered} D_{11} = {\frac{1 - \upsilon }{2}}A_{11} \quad D_{12} = {\frac{1 - \upsilon }{2}}A_{12} \quad D_{13} = {\frac{1 - \upsilon }{2}}A_{13} \quad D_{14} = {\frac{1 - \upsilon }{2}}A_{14} \hfill \\ \quad D_{22} = {\frac{1 - \upsilon }{2}}A_{22} \quad D_{23} = {\frac{1 - \upsilon }{2}}A_{23} \quad D_{24} = {\frac{1 - \upsilon }{2}}A_{24} \quad \hfill \\ \quad D_{33} = {\frac{1 - \upsilon }{2}}A_{33} \quad D_{34} = {\frac{1 - \upsilon }{2}}A_{34} \, \hfill \\ D_{44} = {\frac{1 - \upsilon }{2}}A_{44} \hfill \\ \end{gathered} $$

and D _ij  = D _ji , (i, j = 1 to 4)

The coefficients of matrix [X] are,

$$ \begin{gathered} X_{11} = A_{11} \left( {{\frac{m\pi }{L}}} \right)^{2} \quad X_{12} = 0 \quad X_{13} = A_{12} \left( {{\frac{m\pi }{L}}} \right)^{2} \quad \hfill \\ X_{14} = - A_{15} \left( {{\frac{m\pi }{L}}} \right) \quad X_{15} = A_{13} \left( {{\frac{m\pi }{L}}} \right)^{2} \quad X_{16} = - 2A_{16} \left( {{\frac{m\pi }{L}}} \right)\,\,\,\, \hfill \\ \quad X_{17} = A_{14} \left( {{\frac{m\pi }{L}}} \right)^{2} \quad X_{18} = - 3A_{17} \left( {{\frac{m\pi }{L}}} \right)\,\, \hfill \\ \end{gathered} $$

$$ \begin{gathered} X_{22} = D_{11} \left( {{\frac{m\pi }{L}}} \right)^{2} \quad X_{23} = D_{11} \left( {{\frac{m\pi }{L}}} \right) \quad X_{24} = D_{12} \left( {{\frac{m\pi }{L}}} \right)^{2} \,\,\,\, \hfill \\ X_{25} = 2D_{12} \left( {{\frac{m\pi }{L}}} \right)\quad X_{26} = D_{13} \left( {{\frac{m\pi }{L}}} \right)^{2} \quad X_{27} = 3D_{13} \left( {{\frac{m\pi }{L}}} \right)\,\,\,\, \hfill \\ X_{28} = D_{14} \left( {{\frac{m\pi }{L}}} \right)^{2} \, \hfill \\ \end{gathered} $$

$$ \begin{gathered} X_{33} = A_{22} \left( {{\frac{m\pi }{L}}} \right)^{2} + D_{11} \quad X_{34} = \left( { - A_{25} + D_{12} } \right)\left( {{\frac{m\pi }{L}}} \right) \quad X_{35} = A_{23} \left( {{\frac{m\pi }{L}}} \right)^{2} + 2D_{12} \hfill \\ X_{36} = \left( { - 2A_{26} + D_{13} } \right)\left( {{\frac{m\pi }{L}}} \right)\quad X_{37} = A_{24} \left( {{\frac{m\pi }{L}}} \right)^{2} + 3D_{13} \quad X_{38} = \left( { - 3A_{27} + D_{14} } \right)\left( {{\frac{m\pi }{L}}} \right) \hfill \\ \end{gathered} $$

$$ \begin{gathered} X_{44} = A_{55} + D_{22} \left( {{\frac{m\pi }{L}}} \right)^{2} \quad X_{45} = \left( { - A_{53} + 2D_{22} } \right)\left( {{\frac{m\pi }{L}}} \right) \quad X_{46} = 2A_{56} + D_{23} \left( {{\frac{m\pi }{L}}} \right)^{2} \hfill \\ X_{47} = \left( { - A_{54} + 3D_{23} } \right)\left( {{\frac{m\pi }{L}}} \right) \quad X_{48} = 3A_{57} + D_{24} \left( {{\frac{m\pi }{L}}} \right)^{2}\quad \hfill \\ \end{gathered} $$

$$ \begin{gathered} X_{55} = A_{33} \left( {{\frac{m\pi }{L}}} \right)^{2} + 4D_{22} \quad X_{56} = \left( { - 2A_{36} + 2D_{23} } \right)\left( {{\frac{m\pi }{L}}} \right)\quad X_{57} = A_{34} \left( {{\frac{m\pi }{L}}} \right)^{2} + 6D_{23} \quad \hfill \\ X_{58} = \left( { - 3A_{37} + 2D_{24} } \right)\left( {{\frac{m\pi }{L}}} \right) \hfill \\ \end{gathered} $$

$$ X_{66} = 4A_{66} + D_{33} \left( {{\frac{m\pi }{L}}} \right)^{2}\quad X_{67} = \left( { - 2A_{64} + 3D_{33} } \right)\left( {{\frac{m\pi }{L}}} \right) \quad X_{68} = 6A_{67} + D_{34} \left( {{\frac{m\pi }{L}}} \right)^{2} $$

$$ X_{77} = A_{44} \left( {{\frac{m\pi }{L}}} \right)^{2} + 9D_{13} \quad X_{78} = \left( { - 3A_{47} + 3D_{24} } \right)\left( {{\frac{m\pi }{L}}} \right)$$

$$ X_{88} = 9A_{77} + D_{44} \left( {{\frac{m\pi }{L}}} \right)^{2} $$

and X _ij  = X _ji , (i,j = 1 to 8)