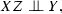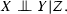Abstract
Information theoretic feature selection methods quantify the importance of each feature by estimating mutual information terms to capture: the relevancy, the redundancy and the complementarity. These terms are commonly estimated by maximum likelihood, while an under-explored area of research is how to use shrinkage methods instead. Our work suggests a novel shrinkage method for data-efficient estimation of information theoretic terms. The small sample behaviour makes it particularly suitable for estimation of discrete distributions with large number of categories (bins). Using our novel estimators we derive a framework for generating feature selection criteria that capture any high-order feature interaction for redundancy and complementarity. We perform a thorough empirical study across datasets from diverse sources and using various evaluation measures. Our first finding is that our shrinkage based methods achieve better results, while they keep the same computational cost as the simple maximum likelihood based methods. Furthermore, under our framework we derive efficient novel high-order criteria that outperform state-of-the-art methods in various tasks.
Similar content being viewed by others
1 Introduction
Feature Selection (FS) is an important dimensionality reduction technique with various applications that range from computer vision (Barbu et al. 2017) to bioinformatics (Bolón-Canedo et al. 2014), and from structure learning (Aliferis et al. 2010) to text mining (Forman 2003). Not only is FS a challenging problem to solve, but also to define, in the form of selecting the set of “optimal” features. Guyon and Elisseeff (2003) categorise FS techniques in three groups: filters, wrappers and embedded. Our work focuses on filter FS, which is the fastest and less likely to overfit, and, in particular, we will be discussing information theoretic FS.
In information theoretic FS, we rank the features according to a score measure. This score should capture three important terms: the relevancy of the feature with the target, the redundancy and the complementarity between the features (Vergara and Estévez 2014). These three terms are functions of two important information theoretic quantities: mutual and conditional mutual information. Estimating these quantities is a very challenging problem. For example, in the case of conditional mutual information the size of the contingency table increases exponentially with the number of features in the conditioning set. As the number of selected features grows the estimates of these quantities are less reliable. To overcome this problem the literature is awash with low-order criteria that try to approximate the original problem (Brown et al. 2012). The main idea is instead of estimating the joint distribution of all features with the target variable, estimate low-order, such as pairwise (i.e. second-order), feature interactions.
In a recent work, Vinh et al. (2016) explored whether high-order feature dependencies improve information theoretic feature selection and they observe that
...in between second-order dependency and full high-order dependency, there is currently no or little research.
The main reason behind the absence of high-order criteria from the literature is that estimating information theoretic quantities between a large number of variables, i.e. groups of features, is a very challenging problem. The vast majority of the FS literature uses maximum likelihood estimators. While this is a fast approach, it is not reliable, especially for small sample scenarios, where they perform very poorly and exhibit substantial bias (Hausser and Strimmer 2009). To this end alternative approaches have been proposed, such as Bayesian (Archer et al. 2013) or shrinkage (Scutari and Brogini 2012). At the current state, the shrinkage methods are the preferred ones, since they are faster than the Bayesian estimator and more accurate than the maximum likelihood estimator.
Shrinkage methods have been used extensively in various research areas (Efron 2012). The main idea behind them is to use a weighted average between two estimators: one high-dimensional (i.e. maximum likelihood) with low bias and high variance, and one low-dimensional, which has high bias and low variance. The two main challenges in applying shrinkage methods is to derive a low dimensional estimator that is suitable for the problem in hand, and to estimate the weight (shrinkage intensity). In the literature of machine learning there have been suggested shrinkage estimators for mutual and conditional mutual information, which simplistically shrink towards the uniform distribution (Hausser and Strimmer 2009; Scutari and Brogini 2012). We improve this point by adopting a more informative yet low-dimensional distribution towards which we smooth the estimates, and we show that it consistently improves over the existing shrinkage methods. Furthermore, by deriving closed form expressions for the shrinkage intensity, our novel estimators have complexity similar to the naive maximum-likelihood, while at the same time they achieve superior performance.
Our novel shrinkage method is particularly suitable for estimating information theoretic terms between variables with large number of categories (bins). This can, for example, occur when we estimate the mutual information I(X; Y) and the feature X and/or the target Y take a large number of possible values. A more interesting scenario, where the same issue arises, is in feature interactions into account, estimates of I(Z; Y) where Z is the joint random variable of \(X_1\), \(X_2\) and \(X_3\). This mutual information is a valuable quantity to know, as it takes the third order feature interactions into account, but it is challenging to be estimated due to the large number of bins. Our estimators are ideally suited to estimate such high dimensional densities, and hence provide a route to detecting high-order feature interactions. The purpose of this article is twofold:
- 1.
To suggest a new data-driven shrinkage approach for estimating mutual and conditional mutual information.
- 2.
To use our estimators to derive high-order FS algorithms by extending two popular state-of-the-art second-order methods: JMI (Yang and Moody 1999) and CMIM (Fleuret 2004).
The remainder of this paper is organised as follows. Section 2 presents the three main ways for estimating information theoretic quantities: frequentist, Bayesian and shrinkage, and provides all the necessary background on information theoretic FS. Section 3 derives a novel shrinkage estimator for mutual and conditional mutual information. Section 4 uses our estimators to derive four novel high-order FS criteria. Sections 5 and 6 present a thorough evaluation of our methods, using 31 datasets from diverse sources and various evaluation measures. Overall, our suggested FS criteria, JMI-3 and CMIM-3, that take into account third-order interactions outperform the state of the art.Footnote 1
2 Background
2.1 Background on estimating mutual information
Shannon’s mutual information (MI) between two variables captures the amount of information that these variable share. Let us assume that we have two categorical variablesFootnote 2X, Y that take values from known alphabets \(x \in {\mathcal {X}}\) and \(y \in {\mathcal {Y}}.\) The MI is defined as follows (Cover and Thomas 2006):
The conditional MI between X and Y given Z is defined as the expectation of \(I(X;Y|Z=z)\) with respect to the distribution of Z:
To estimate MI from sampled data, we need reliable ways for estimating the joint probabilities. For example, for estimating MI we need to estimate the probabilities \(p(xy), \forall x \in {\mathcal {X}},y \in {\mathcal {Y}},\) from sampled data \(\{ x^n,y^n \}_{n=1}^N\). There are three main approaches to estimate these probabilities: frequentist, bayesian and shrinkage.
Frequentist estimators: The simplest, and probably most widely used way to estimate the probability p(xy) is by using the frequency counts – which is the maximum likelihood (ML) estimate: \({\hat{p}}^{\mathrm{ML}}(xy) = \frac{N_{xy}}{N},\) where \(N_{xy}\) is the observed counts of the random variable XY taking the value xy and N is the total number of samples. By substituting these probabilities in eq. (1) we get the ML estimator \( {\hat{I}}^{\mathrm{ML}}(X;Y).\) It is well known that this estimator is biased (Steuer et al. 2002), while there are many works that tried to derive expressions for correcting this bias. As Brillinger (2004) mentioned, the bias correction expressions are messy, and for that reason non-parametric procedures, such as jackknife (JK) or bootstrap, are preferable for estimating information theoretic terms. For example, the JK estimate of the MI is given by the following expression (Paninski 2003): \({\hat{I}}^{\mathrm{JK}}(X;Y) = N {\hat{I}}^{\mathrm{ML}}(X;Y) - \frac{N-1}{N} \sum _{n=1}^N {\hat{I}}^{\mathrm{ML \backslash n}}(X;Y),\) where \({\hat{I}}^{\mathrm{ML}}(X;Y)\) is the ML estimate using all data, while \({\hat{I}}^{\mathrm{ML \backslash n}}(X;Y)\) the ML estimate based on all but the n-th sample. By definition, the JK estimator is \(N+1\) times more complex than the ML estimator.
Bayesian estimators: It is well known that the ML estimator can be improved by using a Bayesian regularisation of the counts (Agresti and Hitchcock 2005). To do so, let us assume a Dirichlet prior distribution with parameters \(\alpha _{xy}\), the posterior distribution is Dirichlet with mean: \({\hat{p}}^{\mathrm{Bayes}}(xy) = \frac{N_{xy}+\alpha _{xy}}{N+A},\) where \( A = \sum _{ x \in {\mathcal {X}},y \in {\mathcal {Y}}} \alpha _{xy}\). The parameters \(\alpha _{xy}\) can be seen as the pseudo-counts, and A as the a-priori sample size. Hutter (2002) introduced the first Bayesian estimator for MI, which relies on a fixed Dirichlet prior, and as a result exhibits a strong prior dependence. To overcome this limitation, Archer et al. (2013) introduced a set of Bayesian estimators of the MI that use a mixture of Dirichlets prior, with mixing weights designed to produce an approximately flat prior over MI. This idea is based on the Nemenman–Shafee–Bialak (NSB) entropy estimator (Nemenman et al. 2002), which uses a mixture of Dirichlets to derive a flat prior over the entropy (H). While the Archer et al. (2013) approach did not lead to strong results, they examined the performance of various Bayesian estimators in a variety of simulated datasets and showed that the Bayesian estimator that achieves the best performance is the one that estimates MI through estimating NSB entropies (H): \({\hat{I}}^{\mathrm{NSB}}(X;Y) = {\hat{H}}^\mathrm{NSB}(X) + {\hat{H}}^{\mathrm{NSB}}(Y) - {\hat{H}}^{\mathrm{NSB}}(xy).\) The main limitations of this estimator are that it is very slow and it does not estimate the joint distribution, and as a result sometimes can give negative estimates of MI. To the best of our knowledge, there is no Bayesian estimator for the conditional MI proposed thus far. One natural way to derive one is by writing the conditional MI as a linear combination of entropies, but this is out of the scope of the current paper.
Shrinkage estimators: Historically, James and Stein (1961) were the first to propose a shrinkage estimator for the mean of multivariate normal distribution. This estimator has many interesting properties, such as that it outperforms the ML estimator in terms of Mean Squared Error (MSE), without additional computational costs. Especially for high-dimensional distributions, James-Stein (JS) type shrinkage estimators dominate the ML (Efron 2012). In the most general form, assuming that we want to estimate one parameter \(\theta ,\) the JS principle can be written as:
where \({\hat{\theta }}\) and \({\hat{\theta }}^{\mathrm{Target}} \) are two different estimators, for the same model. \({\hat{\theta }}\) is a high-dimensional estimator, which has small bias, but high variance, while \({\hat{\theta }}^{\mathrm{Target}} \) is a low-dimensional, which has smaller variance than \({\hat{\theta }}\) but higher bias. The JS estimator is a weighted average between these two estimators, which can be seen as an empirical Bayes estimator with a data-driven choice of priors (Efron 2012).
The main challenge of deriving shrinkage estimators is how to select the optimal value for the shrinkage parameter \(\lambda \). In the literature, some computationally expensive ways to estimate \(\lambda \), such as using cross-validation (Friedman 1989), have been suggested. In a seminal work, Ledoit and Wolf (2003) derived an analytical expression for choosing \(\lambda \) that guarantees minimal MSE, without requiring such computationally expensive procedures. Based on this result, Hausser and Strimmer (2009) suggested the first JS method for estimating categorical probabilities, using as a high dimensional estimator the ML and as a low dimensional target the convenient choice of the uniform distribution:
Hausser and Strimmer (2009) estimated the shrinkage intensity that minimizes MSE and by plugging the estimates derived by Eq. (3) directly in the MI expression of Eq. (1), they derived the first JS estimator for the MI, \({\hat{I}}^{{\text {Uni-JS}}}(X;Y)\). Scutari and Brogini (2012) extended this methodology for estimating the joint probabilities of three variables and derived a JS estimator for the conditional MI, \({\hat{I}}^{{\text {Uni-JS}}}(X;Y|Z)\).
In Sect. 3 we will introduce novel JS estimators for MI and conditional MI that rely on more expressive forms for the low dimensional target. In Sect. 4 we will use these estimators to derive novel information theoretic FS criteria that capture high-order interactions. Before that, in the following subsection we will provide the necessary background on information theoretic FS.
2.2 Background on feature selection
Brown et al. (2012) showed that many information theoretic FS criteria published the last twenty years can be seen as low-order approximations of a clearly specified optimisation problem; maximising the conditional likelihood.Footnote 3 A greedy forward selection to optimise this objective is, at each step k, to select the feature \(X_k \in \mathbf{{X}}_{{\widetilde{\theta }}}\) that maximises the following conditional mutual information (CMI): \(J_{\mathrm{CMI}}(X_k) = {I}(X_k;Y|\mathbf{{X}}_{\theta }),\) where \(\mathbf{{X}}_{\theta }\) is the set of the \((k-1)\) features already selected and \(\mathbf{{X}}_{{\widetilde{\theta }}}\) the unselected ones. As the number of selected features grows, the dimension of \(\mathbf{{X}}_{\theta }\) also grows, and this makes our estimates less reliable. To overcome this issue the literature provides many approaches for deriving low-order criteria (Fleuret 2004; Peng et al. 2005).
Lower-order criteria: Brown et al. (2012) presented two assumptions that proved to be very useful for deriving second-order criteria: the pairwise feature conditional independence assumption and the pairwise class conditional independence assumption (Brown et al. 2012, Assumptions 1 and 2 respectively). Under these assumptions CMI can be decomposed in three terms; by parameterising this decomposition, a space of potential criteria was created as so:
These terms capture three concepts well studied in the FS literature: the ‘relevancy’, the ‘redundancy’ and the ‘complementarity’. The score of each feature \(J'_{CMI }\) will be increased if the relevancy of the feature with the output is high, the redundancy with the existing features is low, and the complementarity with the existing features is high. Complementarity, which is also known as ‘synergy’ or ‘conditional redundancy’, plays a crucial role, since it suggests that selecting correlated features can be useful, provided that the correlation within classes is stronger than the overall correlation (Brown et al. 2012).
The above parametrisation provides a nice connection between criteria suggested in the literature and the framework of the conditional likelihood maximisation. Table 1 presents some popular criteria. The Mutual Information Maximisation (MIM) criterion (Lewis 1992), Eq. (5), can be obtained with \(\beta =\gamma =0,\) which means that it captures only relevance and ignores redundancy and complementarity. The Minimum Redundancy Maximum Relevance (mRMR) (Peng et al. 2005) criterion, Eq. (8), captures redundancy using a normalised coefficient \(\beta = 1/|\mathbf{{X}}_{\theta }|,\) and sets \(\gamma = 0\) thus ignoring complementarity. The Joint Mutual Information (JMI) (Yang and Moody 1999; Meyer et al. 2008) criterion, Eq. (6), can be obtained with \(\beta =\gamma = 1/|\mathbf{{X}}_{\theta }|\). Brown et al. (2012) showed that JMI controls relevancy, redundancy, complementarity and provides a very good tradeoff in terms of accuracy, stability and flexibility. Conditional Mutual Information Maximisation (CMIM) (Fleuret 2004), Eq. (7), is a popular criterion that uses a non-linear combination of information theoretic terms, and it can be decomposed in a similar manner as JMI (Brown et al. 2012).
While the criteria presented so far are the most widely used low-order criteria, in the literature there have been suggested many other heuristics. For example, other popular criteria are MIFS (Battiti 1994), ICAP (Jakulin 2005), CIFE (Lin and Tang 2006) and DISR (Meyer and Bontempi 2006). For a more thorough list of information theoretic criteria, we refer the reader to (Brown et al. 2012; Vergara and Estévez 2014).
Higher-order criteria: Interestingly, under the above framework the terms of redundancy and complementarity are approximated taking into account only pair-wise interactions, i.e. second-order interactions. Recently, Vinh et al. (2016) suggested relax-mRMR, Eq. (9), a novel third-order criterion that relaxes Assumption 1 in Brown et al. (2012). This criterion can be regarded as the JMI with an additional last term that captures third-order interactions between features for the redundancy. Section 4 provides a novel framework for generating any high order criteria by relaxing both assumptions of Brown et al. (2012). We will show that relax-mRMR is a special case of our suggested framework, and we will naturally derive novel higher order criteria.
The most expensive part in the FS algorithms described so far is the calls to estimate the MI (Fleuret 2004). For that reason the criteria presented so far use the fast ML estimator. In the following section we will derive computationally efficient shrinkage estimators, which will be crucial for deriving high-order FS criteria.
Other methods: While our work focuses on deriving information theoretic FS criteria that capture high-order feature interactions, there are studies in the literature that provide answers from other perspectives. For example, there is a recent group of works for significance pattern mining (Terada et al. 2013; Llinares-López et al. 2015; Papaxanthos et al. 2016): finding groups of items (i.e. features) that occur statistically significant more often in one class than in the other, and rigorously controlling the family-wise error rate (FWER). One possible limitation of these methods is that they assume binary items, while in the information theoretic FS there is not restriction in the arity of the features.
3 Deriving novel shrinkage estimators
In this section, firstly, we will derive a novel shrinkage estimator for the joint probability distribution, and then we will show how this estimator can be used to estimate mutual and conditional MI.
3.1 Shrinkage estimator for joint probability distribution
Hausser and Strimmer (2009) suggested a shrinkage estimator, presented in Eq. (3), which derives the low-dimensional target by assuming a uniform distribution over XY: \(XY \sim \mathrm{Unif} \{ {\mathcal {X}} \times {\mathcal {Y}} \}.\) This is an extremely low-dimensional target estimator, with no free parameters, and as a result it imposes a strong structure. This structure can be captured with the following three requirements:

Smoothing the high-dimensional estimate by shrinking towards independence is reasonable, since it improves the estimation of small effect sizes. Small effects, i.e. small I(X; Y), are the challenging ones to estimate, since when the effects are large, it is easier to discriminate between them. On the other hand, simplistically assuming uniform distribution on the marginals creates an over restricted structure. To overcome this restriction, we adopt a more informative low dimensional target –the product of the marginals– by suggesting the following estimator:
Under this structure the low-dimensional target estimator has: \(|{\mathcal {X}}| + |{\mathcal {Y}}| -2\) parameters, while the high-dimensional \(|{\mathcal {X}}||{\mathcal {Y}}|-1\). Our proposed Ind-JS estimator, Eq. (12), can be seen as a generalisation of the estimator presented in Eq. (3) by relaxing requirements (ii) and (iii) in Eq. (11). By providing a data-driven low-dimensional target, we decrease the bias compared to the uniform target of Eq. (3), but we increase the variance, since we use sample estimates instead of the fixed uniform value.
As we already mentioned in Sect. 2.1, the main challenge on deriving shrinkage estimators is the estimation of the optimal shrinkage intensity \({\hat{\lambda }}^{*}\) that minimises the MSE. The following theorem derives the optimal shrinkage intensity of our suggested estimator.
Theorem 1
The shrinkage intensity that minimises the MSE of the estimator suggested in Eq. (12) is given by the following expression:
where the five terms are estimated as follows:
Proof
The proof can be found in Supplementary Material Section A.1. \(\square \)
In finite samples the estimated shrinkage may take negative values or exceed the value of one, leading to negative shrinkage or over shrinkage. To avoid this, following Hausser and Strimmer (2009), we truncate the estimated shrinkage intensity \({\hat{\lambda }}^{**} = \max ( 0, \min (1, {\hat{\lambda }}^*) ).\)
By observing the equation for estimating the shrinkage intensity, Eq. (13), we can get some interesting insights. Firstly, the smaller the variance of the high dimensional estimator, \(\widehat{\mathrm{Var}}\left[ {\hat{p}}^{{\mathrm{ML}}}(xy)\right] \), the smaller the shrinkage intensity \({\hat{\lambda }}^*\). Thus with bigger samples (i.e. asymptotically) the influence of the low-dimensional target vanishes, and converges to the true value, since the high-dimensional estimator (i.e. the ML estimator) is consistent. Secondly, the denominator is equal to the expected squared difference between the two estimators \(\widehat{{\mathbb {E}}}\left[ \left( {\hat{p}}^{{\mathrm{ML}}}(xy) - {\hat{p}}^{{\mathrm{Ind}}}(xy)\right) ^2\right] .\) When this difference is high the shrinkage intensity \({\hat{\lambda }}^*\) is small, which protects the estimate from misspecified low-dimensional targets (Schäfer and Strimmer 2005). Finally, the covariance term, \(\widehat{\mathrm{Cov}}\left[ {\hat{p}}^{{\mathrm{ML}}}(xy),{\hat{p}}^{{\mathrm{Ind}}}(xy)\right] \), adjusts for the fact that both the unrestricted high-dimensional and our low-dimensional estimator are derived from the data. This is an important difference between our method, Ind-JS, and the method presented in Sect. 2.1, Uni-JS. The latter one uses a fixed uniform distribution for the low-dimensional target, ignoring any information contained in the data.
3.2 Shrinkage estimator for mutual information
By estimating the optimal shrinkage intensity using Eq. (13), we can estimate our novel shrinkage estimates for the probabilities, Eq. (12), and by plugging these probabilities in the MI expression of Eq. (1), we can derive a novel shrinkage estimator for the MI:
Now we will empirically compare our novel shrinkage estimator, Eq. (14), with the best frequentist, Bayesian and shrinkage estimators presented in Sect. 2. For completeness, we will also include the ML estimator, which is widely used in the FS literature. We will compare the different estimators in terms of their Mean Squared Error (MSE) and their runtime, i.e. measuring the time in secondsFootnote 4 that was required to perform the estimation. To derive MSE we will generate synthetic datasets, where we have a control over the population value of MI, I(X; Y). Supplementary Material Section B.1 presents our approach for generating datasets \(\{x^n, y^n \}_{n=1}^N,\) and controlling the value of I(X; Y). For the experiments we used a relatively small sample size (\(N=200\) examples) and we assumed a binary target Y and a variable X that takes \(|{\mathcal {X}}| = 25\) distinct values. For example, X can be seen as the joint variable of two features \(X = X_k X_l\) with \(|{\mathcal {X}}_k| = 5,\) and \(|{\mathcal {X}}_l| = 5\). Estimating efficiently \(I(X_k X_l; Y)\) is necessary for the JMI criterion, Eq. (6). In our experiments we explored the MSE for various values of the MI, which were grouped as small/medium/large.Footnote 5
Figure 1 shows that our suggested shrinkage estimator, Ind-JS, outperforms, with statistical significance, all of the other methods for small and medium effects, while for large effects it achieves comparable performance to the computationally demanding Bayesian approach (NSB). Furthermore, our method takes only \(3.3\times \) more time than ML to estimate MI, while JK takes \(200\times \) and NSB \(950\times \) more time. The fact that our estimator outperforms Uni-JS is a result of our data-driven specification of the low-dimensional target. Instead of assuming uniform distributions for X and Y, we estimate the marginals from the data. This improvement over Uni-JS comes without significantly different runtime.
Comparing various MI estimators in terms of their a MSE and b average running time (over 100 repetitions), in log-scale. In (a) the tick above the bars of the competing methods indicates that our method achieves statistically significant (one-sided t-test with p value \(<0.05\)) lower MSE, while the cross indicates not statistically significant different (one-sided t-test with p value \(>0.05\)). For all effect sizes our estimator Ind-JS outperforms, with statistical significance the two estimators with similar runtime ML and Uni-JS. Furthermore, for small and medium effect sizes it outperforms much more computationally demanding methods, such as JK and NSB, while for large effects it achieves comparable performance
Finally, it will be useful to explore whether the suggested estimator is consistent, or in other words, to check if the estimated MI convergences to the true MI as the sample size increases. From a theoretical perspective, as we mentioned in the previous section, with bigger samples (i.e. asymptotically) the influence of the low-dimensional target vanishes in Eq. (13). As a result, the estimated shrinkage probabilities \({\hat{p}}^{\text {Ind-JS}}(xy)\) converge to the consistent ML probabilities \({\hat{p}}^{\mathrm{ML}}(xy)\). A direct consequence of this property is that our suggested MI estimator Uni-JS is also converge asymptotically to the true MI value. To verify this, Fig. 2 presents convergence plots for various MI values, where we see that for all scenarios the estimated value converge to the true one at the sample size increases.
3.3 Shrinkage estimator for conditional mutual information
In the previous section we showed how to improve the estimation of MI by applying a shrinkage towards a low-dimensional estimator, derived under the independence assumption  . To estimate the conditional MI I(X; Y|Z), Eq. (2), we need to estimate the joint probabilities of three variables p(xyz). There are three different types of independence describing three way interactions (Agresti 2013, Sec. 9.2):
. To estimate the conditional MI I(X; Y|Z), Eq. (2), we need to estimate the joint probabilities of three variables p(xyz). There are three different types of independence describing three way interactions (Agresti 2013, Sec. 9.2):
- (a)
the complete (or mutual) independence, when all variables are independent from each other, i.e.

- (b)
the joint independence, when two variables are jointly independent of the third, i.e.
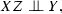
- (c)
the conditional independence, when two variables are independent given the third, i.e.
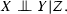
Figure 3 shows the underlying graphical model of these three types. The most general assumption, that implies all of the others, is the mutual independence, which means \(p(xyz) = p(x)p(y)p(z),\) and has \(|{\mathcal {X}}| + |{\mathcal {Y}}| + |{\mathcal {Z}}| -3\) free parameters. As Agresti (2013, Section 9.2) shows, this type of independence can be captured by a model with the smallest number of parameters compared to the models that capture the other two types of independence (joint and conditional). For example, the dimensionality of joint independence is \(|{\mathcal {X}}| |{\mathcal {Z}}| + |{\mathcal {Y}}| -2,\) while that of conditional independence is \((|{\mathcal {X}}| -1)(|{\mathcal {Y}}|-1)|{\mathcal {Z}}|\).
To derive their Uni-JS estimator for the conditional MI (see Sect. 2.1), Scutari and Brogini (2012) defined the low dimensional shrinkage target by assuming mutual independence and uniform probability for the joint: \(XYZ \sim \mathrm{Unif} \{ {\mathcal {X}} \times {\mathcal {Y}} \times {\mathcal {Z}}\}.\) This is extremely low-dimensional, with no free parameters, and as a result it imposes a strong structure. Mutual independence is the most restrictive independence assumption possible, while assuming uniform distribution over the priors creates an even more restrictive structure. In fact this structure is the maximum entropy distribution over the three parameters.
To overcome both of these restrictions, we suggest the following shrinkage approach for estimating the joint probabilities of three variables, where we use a data driven low dimensional shrinkage target that captures the joint independence between XZ and Y, and we do not make any distributional assumption over the marginal probabilitiesFootnote 6:
Under the above structure the low-dimensional estimator has \(|{\mathcal {X}}| |{\mathcal {Z}}| + |{\mathcal {Y}}| -2\) parameters, while the high-dimensional \(|{\mathcal {X}}||{\mathcal {Y}}||{\mathcal {Z}}| -1\). The shrinkage intensity that minimises MSE can be estimated using Theorem 1, by substituting X with the joint variable XZ. By estimating the optimal shrinkage intensity, we can estimate our novel shrinkage estimates for the probabilities, Eq. (15), and use them to derive a shrinkage estimator for the conditional MI: \({\hat{I}}^{\text {Ind-JS}}(X;Y|Z)\).
Similar to the previous section, we will compare the different ways for estimating conditional MI in terms of their MSE. Supplementary Material Section B.2 presents our approach for generating datasets \(\{x^n, y^n ,z^n\}_{n=1}^N,\) and controlling the value of I(X; Y|Z). In the experiments for this section we used a relatively small sample size (\(N=200\) examples) and we assume a binary target Y, a variable \(X_k\) that takes \(|{\mathcal {X}}_k| = 5\) distinct values and a variable \(X_l\) that takes \(|{\mathcal {X}}_l| = 5\). Estimating efficiently the conditional mutual information \(I(X_k; Y| X_l)\) is necessary for the CMIM criterion, Eq. (7). Figure 4 shows that our suggested shrinkage estimator, Ind-JS, outperforms all of the other methods, by requiring almost the same runtime as the simple ML estimator.
Comparing various conditional MI estimators in terms of their a MSE and b average running time (over 100 repetitions), in log-scale. In (a) the tick above the bars of the competing methods indicates that our method achieves statistically significant (one-sided t-test with p value \(<\,0.05\)) lower MSE, while the cross indicates not statistically significant different (one-sided t-test with p value \(>\,0.05\)). For all effect sizes our estimator, Ind-JS, outperforms the other estimators
As we showed in this section, our shrinkage estimators outperform other methods in MSE, without increasing the runtime. In the following section we will use these estimators to suggest high-order FS algorithms.
4 Deriving high-order FS criteria
In this section, firstly, we will suggest a novel decomposition that captures high-order features interactions, then we will present novel FS criteria that capture all the desirable high-order terms for redundancy and complementarity. Finally, we will present a computational complexity analysis and show the importance of having fast methods, such as shrinkage, for estimating MI.
4.1 Theoretical analysis: a novel decomposition for retrofitting high-order criteria
Section 2.2 showed how the full-order CMI criterion can be decomposed in terms that capture second order feature interactions, Eq. (4). To derive a decomposition that captures higher order interactions we should relax Brown et al. (2012, Assumptions 1 and 2). For simplicity, we will focus on third-order, but our framework can be straightforwardly generalised to derive any high-order decomposition.
Assumption 1
(relaxed) For all unselected features \(X_k \in \mathbf{{X}}_{{\widetilde{\theta }}}\) the selected features \(\mathbf{{X}}_{\theta }\) are pairwise conditional independent given \(X_k\):
Assumption 2
(relaxed) For all unselected features \(X_k \in \mathbf{{X}}_{{\widetilde{\theta }}}\) the selected features \(\mathbf{{X}}_{\theta }\) are pairwise class-conditional independent given \(X_k\):
Using these two assumptions, we can derive with the following theorem a novel third-order decomposition of the CMI criterion, Eq. (10).
Theorem 2
(Novel decomposition) Under Assumptions 1 and 2, the CMI criterion, Eq. (10), is decomposed in the following five terms:
Proof
The proof can be found in Supplementary Material Section A.2. \(\square \)
By suggesting relaxed versions for Assumptions 1 and 2, we can capture three-way feature interaction for both redundancy and complementarity by the fourth and fifth term respectively of Eq. (16). By parameterising our novel decomposition, we can generate a space of new criteria:
The coefficients \(\beta \) and \(\beta '\) control the magnitude of the redundancy terms, the first by controlling the two-way feature interaction terms, and the second, the three-way terms. Furthermore, coefficients \(\gamma \) and \(\gamma '\) control the magnitude of the complementarity terms, by controlling the two-way and three-way feature interactions respectively.
At this point, it is interesting to mention that relax-mRMR (Vinh et al. 2016), presented in Eq. (9), the only information theoretic criterion suggested in the literature that takes into account three-way interactions between features, can be derived by \(J''_{\mathrm{CMI}}\) by setting \(\beta = \gamma = 1/|\mathbf{{X}}_{\theta }|,\)\(\beta ' = 1/|\mathbf{{X}}_{\theta }|(|\mathbf{{X}}_{\theta }|-1)\) and \(\gamma '=0\). Setting to zero the last coefficient means that relax-mRMR ignores the complementarity terms derived by three-way feature interactions.
Different values for the four coefficients lead naturally to different FS criteria. For example by setting all the values to one, \(\beta = \beta ' = \gamma = \gamma ' = 1\) we can derive a criterion similar to CIFE (Lin and Tang 2006), that captures third-order interactions. Brown et al. (2012) showed that for the second-order criteria, when the coefficients \(\beta \) and \(\gamma \) average over the current redundancy and synergy terms, i.e. JMI and CMIM, the criteria achieve the best tradeoff in terms of accuracy and stability. This averaging can be interpreted as a form of “smoothing” that enables the criteria to be resistant to poor estimations of mutual information terms. In the next section we will suggest criteria that use this type of smoothing and capture all desirable high-order interaction terms.
4.2 Extending JMI/CMIM to capture arbitrary high-order interactions
Brown et al. (2012) showed experimentally that JMI and CMIM capture all three desirable terms: relevancy, redundancy and complementarity, and provide a very good tradeoff in terms of accuracy and stability. By design these two criteria capture only second-order feature interactions for estimating redundancy and complementarity. As a result, it is interesting to extend these two criteria in order to handle any higher-order interaction.
A natural way to extend JMI, Eq. (6), is instead of taking the joint between pairs of features, to use any high-order tuple. Similarly, CMIM, Eq. (7) can be extended by conditioning to more than one feature. For example the following two criteria, JMI-3 and CMIM-3, capture third order feature interactions:
The following theorem shows that JMI-3, captures all of the five desirable terms of the decomposition presented in Theorem 2.
Theorem 3
(Decomposing JMI-3) The JMI-3 criterion can be decomposed in the five terms of Eq. (17) with the following coefficients: \(\beta = \gamma = 1/|\mathbf{{X}}_{\theta }|,\) and \(\beta ' = \gamma '= 1/|\mathbf{{X}}_{\theta }|(|\mathbf{{X}}_{\theta }|-1).\)
Proof
The proof can be found in Supplementary Material Section A.3. \(\square \)
The following theorem shows that also CMIM-3 can be decomposed again in the five terms of Theorem 2.
Theorem 4
(Decomposing CMIM-3) The CMIM-3 criterion can be decomposed as:
Proof
The proof can be found in Supplementary Material Section A.4. \(\square \)
Due to the max operator, the interpretation of CMIM-3 decomposition is less straightforward, but it is still clear that it adopts the same assumptions as JMI-3. Our suggested third-order criteria capture all desirable terms for third-order interactions in redundancy and complementarity.
While JMI-3/CMIM-3 capture third-order interactions, they can be extended to any order. For example, the fourth order versions are:
As we see, JMI-3 and CMIM-3 involve the estimation of mutual and conditional MI between four random variables, i.e. three features and the target, while the four order criteria JMI-4 and CMIM-4, between five random variables. Thus, in order to have reliable scores for these two criteria, we need reliable ways (i.e. small MSE) for estimating these high dimensional information theoretic quantities. Furthermore, in each step the criteria estimate a large number of MI terms, so we also need estimators that are fast. In the previous section we saw that our shrinkage estimator achieves the best trade-off between MSE and execution time. Therefore it would be a promising approach for reliable estimation of the score of these third and fourth order criteria.
Algorithm 1 presents a forward selection algorithm that implements JMI-3, while JMI-4, CMIM-3 and CMIM-4 are implemented by uncommented lines 6, 7 and 8 respectively. At this point we should clarify that Algorithm 1 describes the selection procedure for all features when the selected set size is above either \(K=3\) or \(K=4\), for JMI-3/CMIM-3 and JMI-4/CMIM-4 respectively. To select the first feature we use a simple MI ranking as used in JMI, mRMR, CMIM etc, to select the second feature we use either CMIM or JMI, and to select the third feature in the case of JMI-4/CMIM-4 we use JMI-3/CMIM-3.

Notation: From now on we will use the notation \(J_{{\mathrm{FS method}}}^{{\mathrm{Estimator}}}\) to describe both the FS criterion and the estimator used to calculate the score for each criterion. For example \(J_{\text {CMIM-3}}^{\text {Ind-JS}}\), is the CMIM-3 criterion using \({\hat{I}}^{{\text {Ind-JS}}}(X;Y|Z)\) for estimating the conditional MI terms, while \(J_{\text {JMI-4}}^{\text {Ind-JS}}\) is the JMI-4 criterion using \( {\hat{I}}^{{\text {Ind-JS}}}(X;Y)\) for estimating MI terms.
The following section presents a complexity analysis for our suggested FS algorithms.
4.3 Complexity analysis
Let us assume that we have a dataset of N examples and M features and we want to select the top-K. Estimating mutual and conditional MI through ML or our novel shrinkage estimator, Ind-JS, admits a time complexity of O(N), since we need to visit all the examples to estimate the probabilities. Other estimators, such as JK or NSB, increase the complexity by additional factors. For example, for JK that factor depends on the total number of samples, while for NSB it depends on the number of integrand evaluations required for the numerical integration.
Vinh et al. (2016) derived the complexity of second-order FS algorithms for selecting the top-K features. The second-order methods presented in Sect. 2.2, such as mRMR, JMI, CMIM, MIFS, ICAP, CIFE and DISR, require \(O(K^2M)\) calculations of MI and an overall complexity of \(O(K^2MN)\). With appropriate memoisation, using O(M) additional memory, selecting each feature requires O(M) mutual information calculations, one calculation per unselected feature when combined with the most recently selected feature. The terms for previously selected features are stored, and this cache is updated with the newly selected feature’s interactions. As a result, by this memoisation, selecting K features requires O(KM) calculations of MI.Footnote 7 This gives an overall complexity of O(KMN) for second-order feature selection algorithms, using either the ML estimator or shrinkage estimators.
The complexity in terms of the number of mutual information calculations of our third-order criteria, JMI-3/CMIM-3, is \(O(K^3M)\), and the fourth order criteria, JMI-4/CMIM-4, is \(O(K^4M)\). Via a similar memoisation strategy the third and fourth-order criteria can have a factor of K removed, as in the third-order case selecting a feature requires \(O(K^2M)\) mutual information calculations, and the fourth-order case requires \(O(K^3M)\) calculations. This leads to an overall complexity of \(O(K^2MN)\) for the third order criteria, and \(O(K^3MN)\) for the fourth order, using our novel shrinkage estimator.
Table 2 summarises the complexities (with and without memoisation) of the various FS criteria that we will use in the experiments of this work, Sects. 5 and 6. The reported complexities are valid when we estimate MI through ML or shrinkage estimators. As we already mentioned above, using other estimators, such as JK or Bayesian (i.e. NSB) increase the complexity by an extra factor.
FS algorithms that use high-order criteria are more computationally demanding, since they take into account more information by estimating a large number of MI terms. Section 6.3 shows that our estimator, Ind-JS, provides a computationally efficient way for high-order FS.
5 Experiments with data generated from benchmark Bayesian networks
In this section we will use benchmark Bayesian Networks (BN) to generate datasets and we will compare the different FS methods in terms of how accurately they return the optimal feature set. In this scenario we can assume, under some certain assumptions such as faithfulness, that for each node (variable) of the network, the set of the optimal features required for predicting that node is its Markov Blanket (MB) (Aliferis et al. 2010). The MB is defined as the minimal set of features, conditioned on which, all other measured variables become independent. In our work we will use 11, widely used in the literature, benchmark BN to generate various scenarios for feature selection where we know the ground truth of the optimal feature set. Supplementary Material Table 1 presents a summary of these networks. For target variables we used nodes that have at least one child, one parent and one spouse in their MB, which means that the minimum MB size is 3. Overall we generated 296 FS tasks.
Furthermore, the size of the set of the optimal features set (size of MB) varies considerably across the networks, e.g. in andes the average MB size is 7.32. To evaluate the performance of each feature ranking procedure, we will measure the True Positive Rate (TPR) in terms of how many variables are correctly identified in the top-K positions of the ranking, where K is set to the actual length of the MB. Setting a common k for each ranking criterion ensures a fair comparison, and makes reporting the False Positive Rate (FPR) unnecessary since: FPR \(= 1\, - \) TPR. Using the generated FS tasks, we will explore empirically a series of interesting questions for the performance characteristics of the different methods.
5.1 Using Ind-JS estimator to improve ML based high-order FS
As we already mentioned, the default estimator for most FS criteria is the ML (Brown et al. 2012). In this section we will explore how our suggested shrinkage estimator, Ind-JS, can improve the performance of our two third-order criteria, JMI-3 and CMIM-3.
Table 3a focuses on the JMI-3 criterion and shows that for small sample sizes (500 examples) our estimator outperforms ML with statistical significance in most networks. Specifically, in seven out of eleven networks Ind-JS achieves statistically significantly higher TPR than ML. For large sample sizes (2500 examples) in the majority of the networks the two estimators have similar performance, since there is not statistically significant difference in seven of them, while in the remaining four our estimator achieves better performance. Similar result hold for the CMIM-3 criterion (Table 3b). The superior performance of our estimator for small samples is expected, since it is known that the shrinkage approaches are tailored to these scenarios (Hausser and Strimmer 2009).
5.2 Comparison between our suggested high-order FS criteria
In this section we will compare the four novel high-order criteria JMI-3, JMI-4, CMIM-3 and CMIM-4. For all of them we used Ind-JS estimator to calculate the scores. Supplementary Material Table 3 summarises our results, while the critical difference (CD) diagramsFootnote 8 are presented in Fig. 5. Overall, our third order approach, JMI-3, outperforms the rest of the methods in both small and large sample size settings.
CD diagrams for the TPR across the 11 Bayesian networks comparing our four high-order criteria. As the sample sizes increases, fourth-order criteria such as JMI-4 and JMI-4, improve their average score, while the opposite happens with the third-order. JMI-3 outperforms the rest of the methods for both sample sizes
We note that the CMIM family of algorithms have similar criteria to MMPC and its variants. MMPC has a two phase selection algorithm, first forward selection via the maximum of the minimum conditional mutual informations (like CMIM), then backwards selection to remove false positives. It is shown in Aliferis et al. (2010) that this maximum of the minimum approach is sufficient to select parent and child nodes, but it requires a further step to find spouse nodes. As CMIM-3 and CMIM-4 just contain the initial forward selection procedure, they cannot discover spouse nodes (as a spouse node has a higher mutual information when conditioned on the common child node, yet the minimum in CMIM will discard this information), resulting in their relatively poor performance in this Markov Blanket discovery task.
Another interesting conclusion is that the fourth-order method JMI-4, has poor performance in small sample sizes comparing to the third-order method JMI-3 (Fig. 5a). When we increase the sample size (Fig. 5b) the fourth order criterion improves its position in the ranking. The same conclusion holds for CMIM-3 and CMIM-4. This is an expected result, if we consider that with the larger the sample size, the more reliable the high dimensional densities, which are involved in JMI-4 or CMIM-4, are estimated.
5.3 Comparing our best criterion with state-of-the-art methods in terms of TPR
Now we will compare our best high-order criterion JMI-3, which uses our shrinkage estimator Ind-JS to estimate third-order MI terms, i.e. \(J_{\text {JMI-3}}^{\text {Ind-JS}}\), with 10 criteria from the literature of feature selection: MIM Lewis (1992), MIFS (\(\beta = 1\)) (Battiti 1994), CMIM (Fleuret 2004), ICAP (Jakulin 2005), mRMR (Peng et al. 2005), CIFE (Lin and Tang 2006), DISR (Meyer and Bontempi 2006), JMI (Yang and Moody 1999; Meyer et al. 2008), CMI (Brown et al. 2012), relax-MRMR (Vinh et al. 2016).
We used the 11 BN to generate datasets with two different sample sizes: 500 and 2500. Supplementary Material Table 4 summarises our results, while the CD diagrams are presented in Fig. 6. We see that our JMI-3 method, which takes into account third-order interactions for estimating redundancy and complementarity, outperforms the rest of the methods for both sample sizes. Furthermore, the more we increase the sample size, the more our suggested method improves its ranking score (from 1.818 to 1.636), which makes it also sample efficient.
6 Experiments with UCI datasets
In the experiments so far we used BN to generate the datasets, and as a result, we had access to the ground truth of the optimal features (i.e. the MB of each node). In most real world problems we do not have this information, and as as a result it is impossible to estimate evaluation measures such as the TPR. In this section we will explore how the FS criteria perform in terms of the misclassification error, an evaluation measure extensively used in the literature of FS. For this set of experiments we will use 20 datasets from the UCI repository (a summary of them can be found in Supplementary Material Table 2). These datasets have a big variety of characteristics, in terms of number of examples, classes, features, and feature types.Footnote 9 After the FS step we use a nearest neighbour classifier (setting the number of neighbours to 3). Using nearest neighbour classifier is a common practice in FS literature, since this classifier makes few assumptions about the data (Brown et al. 2012). We perform 30 random splits of the data into 50% training and 50% testing, reporting average testing error. To avoid bias related to the number of selected features, we average the classification errors over feature sets whose size is ranging betweenFootnote 10 top-\(K = 1{-}20\).
6.1 Comparing our high-order criteria with state-of-the-art methods
In this section we will compare our four suggested methods JMI-3, JMI-4, CMIM-3 and CMIM-4 (details in Sect. 4.2) with the 10 criteria from the literature of FS (details in Sect. 5.3). Supplementary Material Table 5 summarises our results, while the CD diagram is presented in Fig. 7. Our CMIM-3 criterion is the method that achieves the smallest misclassification error (average rank 5.1). This shows that our third-order criteria outperform competing methods not only in terms of TPR but also in terms of other evaluation measures, such as the misclassification error.
6.2 Sample size and high-order FS
Figure 7 shows that on average CMIM-3 outperforms CMIM, but the difference between their performance is not big (average rank 5.1 vs. 5.5). To identify under which circumstances we have significant benefits from our higher-order methods, we will explore how the different order methods perform in different sample sizes.
Figure 8 compares the classification error of CMIM, CMIM-3 and CMIM-4, which are the second, third and forth order versions of CMIM respectively, in small and large datasets. Figure 8a shows that for small datasets, CMIM-3 and CMIM achieve the same performance, but for large datasets, Fig. 8b, our methods outperforms CMIM with statistically significant difference. Furthermore, we observe that the larger the sample size the better the performance of our third and fourth order criteria. Similar results hold and for the JMI based criteria (Fig. 9).
CD diagrams for comparing the misclassification error of the three CMIM based methods across a 13 small datasets (sample size \(<2000\)), b 7 large datasets (sample size \(> 2000\)). For larger datasets, our high-order criteria outperform CMI, and CMIM-3 outperforms CMI with statistically significant difference
6.3 Efficiency of MI estimators and FS methods
In this section, firstly we will provide a runtime comparison across the different MI estimators, and then across the different FS criteria.
6.3.1 Runtime comparison of different MI estimators
Table 4 presents a run time comparison for the high-order criteria JMI-3 and JMI-4 using various estimators for the MI to select the top-20 features of two UCI datsets: ionosphere, a small dataset of 351 examples and 30 features, and semeion, a large dataset of 1593 examples and 259 features. As we observe our suggested estimator, Ind-JS, is almost as fast as ML (1.1–1.2 times slower), while complex estimators are much slower. For example, in order to derive the top-20 features of semeion using JMI-4, with the JK estimator we need 529 minutes, with the Bayesian NSB estimator we need 234 minutes, while with our shrinkage Ind-JS only 3 minutes.
6.3.2 Runtime comparison of different FS criteria
Figure 10 shows a runtime comparison for various order FS criteria in the two datasets (ionosphere and semeion). For all methods we used an implementation that memorised the score for each feature in each step (details in Sect. 4.3). As we were expected, the higher-order methods (i.e. third and fourth) are more computationally demanding, since they are estimating larger number of MI terms.
Vinh et al. (2016) suggested a straightforward method to parallelise relax-mRMR, which can be used for deriving parallelised versions of our suggested high-order criteria. Furthermore, we note that the CMIM-3 and CMIM-4 algorithms admit a fast implementation similar to the one described in Fleuret (2004), which while it keeps the same complexity class, in practice on most datasets requires far fewer mutual information calculations. We would expect that as the criteria take the minimum over a larger conditioning set that most features would rapidly have their score reduced towards zero, which removes them from consideration as they do not score better than the current best feature. As scores are only updated when an unselected feature is more highly scored than the current best candidate feature it will have the effect of reducing the overall number of calculations. Finally, Liu and Ditzler (2017) introduced a fast approximation to speed up the greedy search of the JMI criterion, by performing approximations on many of the terms in the greedy search. This methodology can be extended to derive fast approximations of JMI-3 and JMI-4. We leave the implementation of these fast versions of JMI-3, JMI-4, CMIM-3 and CMIM-4 for future work.
7 Conclusions and future work
In this work we have introduced novel shrinkage estimators for mutual and conditional mutual information. Our estimators outperform other methods with similar complexity, such as ML, while they achieve competitive performance against more complex methods, such as Bayesian or resampling based (i.e. JK) estimators. Overall, our estimators achieve the best trade-off between MSE and execution time.
We have also derived a framework for generating high-order FS criteria that satisfy desired properties. For example, we proved that two third-order criteria, JMI-3 and CMIM-3, capture the important property of taking into account three way feature interactions for estimating both redundancy and complementarity. Furthermore, we showed that the high-order FS criteria can be improved by using our novel shrinkage estimators instead of the ML. The benefits from using our estimators are more pronounced in the extremely challenging scenarios of having small sample data. Finally we performed a thorough empirical study in various datasets, using various evaluation measures, and we showed that our third-order methods achieve, on average, better performance than the state of the art.
Advice for the Practitioner: Practitioners that need to estimate mutual and conditional MI and deal with small sample sizes can use our novel shrinkage estimator, Ind-JS, since it provides a fast and accurate alternative to the traditional approaches. It is almost as fast as the widely used ML, and as accurate as more computationally demanding approaches, e.g. resampling based or Bayesian. At this point we should emphasise that our novel estimators can be used with any information theoretic or machine learning procedure that requires the estimation of mutual or conditional MI. For example, we can use them to derive predictive biomarkers from clinical trial data (Sechidis et al. 2018), or to derive risk factors in under-reported epidemiological data (Sechidis et al. 2017).
Practitioners that want to select the optimal set of features can consider using our higher-order criteria. With enough data, in the cases we explored \(\sim 2k\) examples, our third order methods (JMI-3 and CMIM-3) outperform, and in some cases with statistically significance difference, the second order alternatives (JMI and CMIM). Choosing between JMI-3 and CMIM-3 is problem dependent. For example, if we are interested on deriving the MB for interpretability we should use JMI-3, while if we are interested in improving the misclassification error of a nearest neighbour classifier, CMIM-3 is a better option. Furthermore, with even more data, the fourth order methods (JMI-4 and CMIM-4) may lead to better performance, but with a factor increase in complexity. To sum up, we suggest the use of our third order criteria with our novel shrinkage estimator, since they provide a good trade off between high accuracy (low error) and without prohibitive high computational cost.
Future work: This work opens many research directions. Firstly, the practicality of our high-order criteria will be improved by deriving fast approximations, and indeed Sect. 6.3.2 outlines some promising ideas towards this direction.
While our suggested methods can be used to derive feature rankings, an interesting extension will be to suggest algorithms that select the optimal number of features. One way is to use a hypothesis testing procedure with our shrinkage estimators to decide whether to continue selecting features, or to stop. For that reason we need to derive the sampling distribution of these estimators. In the case of shrinkage methods, this is not an easy task. A promising research direction is to use resampling approaches, such as the type III parametric bootstrap, which is used extensively to derive credible intervals of empirical Bayes estimators (Carlin and Louis 2008, Sec. 3.5).
Furthermore, in our work we showed that JMI-3/CMIM-3 outperform JMI/ CMIM, especially when the sample size is large enough to reliably estimate the high dimensional densities. But we also showed that JMI-3/CMIM-3 usually perform better than JMI-4/CMIM-4, which means that taking higher-order interactions does not always lead to better results. As a result, it is very important to derive a set of rules to decide which is the “optimal” order for a given sample size. One possible direction is to use the sampling distribution of the estimators and perform sample size determination for observing given MI quantities with a particular statistical power (Sechidis and Brown 2018).
Data access statement
All research data supporting this publication are directly available within this publication.
Change history
04 June 2020
There was a mistake in the proof of the optimal shrinkage intensity for our estimator presented in Section 3.1.
Notes
The software related to this paper, including implementations of our novel estimators and FS criteria, will be available at: https://github.com/sechidis.
Our work focuses on estimating MI between categorical features, but Sect. 6 shows how we can use our results in datasets with continuous features.
Brown et al. (2012) presented two heuristics for optimising this objective, which consider sequentially features one-by-one for adding or removal; the forward selection and the backward elimination respectively. For simplicity from now on we will focus on the forward selection procedure but all of our results are more general and independent of the optimisation procedure.
We report CPU running time and all the experiments were conducted on a PC with Intel ®Core(TM) i5-2400 CPU @ 3.10GHz and 8GB RAM, on a 64-bit Windows 7 OS.
These categories were derived by estimating all possible MI values between the target and features/feature-pairs in 20 UCI datasets (Supplementary Material Table 2). We used the 25% percentile(MI\(\approx 0.05\)) and the 75% percentile (MI\(\approx 0.15\)), to define the three groups: Small effects \(0 <I(X;Y) \le 0.05,\) Medium \( 0.05 < I(X;Y) \le 0.15\) and Large \(I(X;Y) > 0.15.\)
At this point we should clarify that due to the fact that the low dimensional target captures the joint independence between XZ and Y, in general: \({\hat{p}}^{\text {Ind-JS}}(xyz) \ne {\hat{p}}^{\text {Ind-JS}}(xzy).\)
This implementation approach can be seen in the FEAST library Brown et al. (2012), though due to an implementation inefficiency most of the algorithms use O(KM) memory when O(M) would suffice.
For all the CD diagrams of this work, groups of methods that are not significantly different at level \(\alpha = 0.10\) are connected. The method that achieves the best performance is given a rank of 1, the second best a rank of 2, etc.
For estimating mutual information, continuous features were discretised, using an equal-width strategy into 5 bins, a commonly used method in FS literature (Brown et al. 2012).
For the five datasets with less than 20 features (wine, heart, liver, congress and pima), all features are incrementally selected.
References
Agresti, A. (2013). Categorical data analysis (3rd ed.). New York: Wiley.
Agresti, A., & Hitchcock, D. B. (2005). Bayesian inference for categorical data analysis. Statistical Methods and Applications, 14(3), 297–330.
Aliferis, C. F., Statnikov, A., Tsamardinos, I., Mani, S., & Koutsoukos, X. D. (2010). Local causal and markov blanket induction for causal discovery and feature selection for classification part I: Algorithms and empirical evaluation. Journal of Machine Learning Research (JMLR), 11, 171–234.
Archer, E., Park, I. M., & Pillow, J. W. (2013). Bayesian and quasi-Bayesian estimators for mutual information from discrete data. Entropy, 15(5), 1738–1755.
Barbu, A., She, Y., Ding, L., & Gramajo, G. (2017). Feature selection with annealing for computer vision and big data learning. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 39(2), 272–286.
Battiti, R. (1994). Using mutual information for selecting features in supervised neural net learning. IEEE Transactions on Neural Networks, 5(4), 537–550.
Bolón-Canedo, V., Sánchez-Marono, N., Alonso-Betanzos, A., Benítez, J. M., & Herrera, F. (2014). A review of microarray datasets and applied feature selection methods. Information Sciences, 282, 111–135.
Brillinger, D. R. (2004). Some data analyses using mutual information. Brazilian Journal of Probability and Statistics, 18, 163–182.
Brown, G., Pocock, A., Zhao, M.-J., & Lujan, M. (2012). Conditional likelihood maximisation: A unifying framework for information theoretic feature selection. Journal of Machine Learning Research (JMLR), 13, 27–66.
Carlin, B. P., & Louis, T. A. (2008). Bayes and empirical Bayes methods for data analysis (3rd ed.). Boca Raton: Chapman & Hall.
Cover, T. M., & Thomas, J. A. (2006). Elements of information theory (2nd ed.). New York: Wiley.
Efron, B. (2012). Large-scale inference: Empirical Bayes methods for estimation, testing, and prediction (Vol. 1). Cambridge: Cambridge University Press.
Fleuret, F. (2004). Fast binary feature selection with conditional mutual information. Journal of Machine Learning Research (JMLR), 5, 1531–1555.
Forman, G. (2003). An extensive empirical study of feature selection metrics for text classification. Journal of Machine Learning Research (JMLR), 3(Mar), 1289–1305.
Friedman, J. H. (1989). Regularized discriminant analysis. Journal of the American Statistical Association, 84(405), 165–175.
Guyon, I., & Elisseeff, A. (2003). An introduction to variable and feature selection. Journal of Machine Learning Research (JMLR), 3, 1157–1182.
Hausser, J., & Strimmer, K. (2009). Entropy inference and the james-stein estimator, with application to nonlinear gene association networks. Journal of Machine Learning Research (JMLR), 10, 1469–1484.
Hutter, M. (2002). Distribution of mutual information. In T. G. Dietterich, S. Becker, & Z. Ghahramani (Eds.), Advances in neural information processing systems (NIPS) (pp. 399–406). MIT Press.
Jakulin, A. (2005). Machine learning based on attribute interactions. Ph.D. thesis, University of Ljubljana, Slovenia.
James, W., & Stein, C. (1961). Estimation with quadratic loss. In Proceedings of the Fourth Berkeley symposium on mathematical statistics and probability, Volume 1: Contributions to the theory of statistics (pp. 361–379). University of California Press.
Ledoit, O., & Wolf, M. (2003). Improved estimation of the covariance matrix of stock returns with an application to portfolio selection. Journal of Empirical Finance, 10(5), 603–621.
Lewis, David D. (1992). Feature selection and feature extraction for text categorization. In Proceedings of the workshop on Speech and Natural Language.
Lin, D., & Tang, X. (2006). Conditional infomax learning: an integrated framework for feature extraction and fusion. In European conference on computer vision (ECCV)
Liu, H., & Ditzler, G. (2017). A fast information-theoretic approximation of joint mutual information feature selection. In IJCNN (pp. 4610–4617).
Llinares-López, F., Sugiyama, M., Papaxanthos, L., & Borgwardt, K. (2015). Fast and memory-efficient significant pattern mining via permutation testing. In Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining (pp. 725–734). ACM.
Meyer, P. E., & Bontempi, G. (2006). On the use of variable complementarity for feature selection in cancer classification. In Works on the application of evolutionary algorithms.
Meyer, P. E., Schretter, C., & Bontempi, G. (2008). Information-theoretic feature selection in microarray data using variable complementarity. IEEE Journal of Selected Topics in Signal Processing, 2(3), 261–274.
Nemenman, I., Shafee, F., & Bialek, W. (2002). Entropy and inference, revisited. In T. G. Dietterich, S. Becker, & Z. Ghahramani (Eds.), Advances in neural information processing systems (NIPS) (pp. 471–478). MIT Press.
Paninski, L. (2003). Estimation of entropy and mutual information. Neural Computation, 15(6), 1191–1253.
Papaxanthos, L., Llinares-López, F., Bodenham, D., & Borgwardt, K. (2016). Finding significant combinations of features in the presence of categorical covariates. In D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, & R. Garnett (Eds.), Advances in neural information processing systems (pp. 2279–2287). Curran Associates, Inc.
Peng, H., Long, F., & Ding, C. (2005). Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 27(8), 1226–1238.
Schäfer, J., & Strimmer, K. (2005). A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Statistical Applications in Genetics and Molecular Biology, 4(1), 1175–1189.
Scutari, M., & Brogini, A. (2012). Bayesian network structure learning with permutation tests. Communications in Statistics—Theory and Methods, 41(16–17), 3233–3243.
Sechidis, K., & Brown, G. (2018). Simple strategies for semi-supervised feature selection. Machine Learning, 107(2), 357–395.
Sechidis, K., Sperrin, M., Petherick, E. S., Lujn, M., & Brown, G. (2017). Dealing with under-reported variables: An information theoretic solution. International Journal of Approximate Reasoning, 85, 159–177.
Sechidis, K., Papangelou, K., Metcalfe, P. D., Svensson, D., Weatherall, J., & Brown, G. (2018). Distinguishing prognostic and predictive biomarkers: An information theoretic approach. Bioinformatics, 1, 12.
Steuer, R., Kurths, J., Daub, C., Weise, J., & Selbig, J. (2002). The mutual information: Detecting and evaluating dependencies between variables. Bioinformatics, 18(Suppl 2), S231–S240.
Terada, A., Okada-Hatakeyama, M., Tsuda, K., & Sese, J. (2013). Statistical significance of combinatorial regulations. Proceedings of the National Academy of Sciences, 110(32), 12996–13001.
Vergara, J. R., & Estévez, P. A. (2014). A review of feature selection methods based on mutual information. Neural Computing and Applications, 24(1), 175–186.
Vinh, N. X., Zhou, S., Chan, J., & Bailey, J. (2016). Can high-order dependencies improve mutual information based feature selection? Pattern Recognition, 53, 46–58.
Yang, H. H., & Moody, J. (1999). Data visualization and feature selection: New algorithms for nongaussian data. In S. A. Solla, T. K. Leen, & K. Müller (Eds.), Advances in neural information processing systems (NIPS) (pp. 687–693). MIT Press.
Acknowledgements
K.S. research was funded by the AstraZeneca Data Science Fellowship at the University of Manchester. G.B. was supported by the EPSRC LAMBDA Project [EP/N035127/1]. A.Z. and G.C. were supported from the Swiss NSF grant IZKSZ2–162188.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Editors: Karsten Borgwardt, Po-Ling Loh, Evimaria Terzi, Antti Ukkonen.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sechidis, K., Azzimonti, L., Pocock, A. et al. Efficient feature selection using shrinkage estimators. Mach Learn 108, 1261–1286 (2019). https://doi.org/10.1007/s10994-019-05795-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-019-05795-1