Thermochemistry of Bu₄NBr solutions in binary solvents containing formamide

Abstract

The heats of solution of tetrabutylammonium bromide have been measured in mixtures of formamide (FA) with methanol (MeOH) and ethylene glycol (EG) at 313.15 K by calorimetric method. The standard enthalpies of solution in binary mixtures have been extrapolated to infinite dilution by Redlich–Rosenfeld–Meyer type equation using the literary data at 298.15 K and the present paper data at 313.15 K. The Debye–Hückel limiting law slope A _H required for calculation of the ∆_sol H ⁰ value has been obtained with application the new additive scheme of determination of the physic-chemical characteristics of binaries. The scheme is tested on the example of Bu₄NBr solutions in FA–MeOH mixture at 298.15 K. Its application yields the ∆_sol H ⁰ value very closed on the ones determined with the real (non-additive) characteristics of binaries. The standard enthalpies of solution extrapolated by Redlich–Rosenfeld–Meyer type equation are in a good agreement with the ones computed in terms of the Debye–Hückel theory in the second approximation. The heat capacities characteristics of Bu₄NBr have been calculated in H₂O–FA, MeOH–FA and EG–FA mixtures using the literary and present data. The sequence of solvents H₂O > FA > EG > MeOH located on their ability to solvophobic solvation found by us earlier for enthalpic characteristics is confirmed by the ∆C _p ⁰ values. The comparison of thermochemical characteristics of Bu₄NBr solutions in aqueous and non-aqueous mixtures containing FA has been carried out. The own structure of water remains in the region of small additions of formamide to co-solvents. It considerably differs the H₂O–FA mixture from the investigated non-aqueous systems.

Introduction

The binary solvents containing FA have been of wide interest to solution chemists during recent years. Mixtures of FA with water and alcohols including MeOH are intensively studied by various methods [1–11]. In spite of the fact that methanol and water differ strongly in the structure and properties in a liquid state their mixtures with FA have unique similar thermal features. So, the heats of mixing of components have not only the same sign for mixtures of methanol–FA and water–FA but also closed values equal for equimolar composition of given mixtures 0.28 [8] and 0.27 [11] kJ mol⁻¹, accordingly, at 298.15 K. Contrary to it the value of H ^E of the ethylene glycol–formamide system is closed to zero (−0.03 kJ mol⁻¹ [12]). The standard heat of solution of FA in methanol 2.22 kJ mol⁻¹ (our calculation by Eq. 1 from [8]) only a little differs from the heat of solution of FA in water 2.03 [13], 1.97 [14] kJ mol⁻¹ whereas the enthalpy of solution of FA in ethylene glycol is equal to −0.13 kJ mol⁻¹ [15] at 298.15 K. The standard heat of solution of methanol in FA 1.02 (calculation by Eq. 1 from [8]), 0.84 [16] kJ mol⁻¹ not much differs from the heat of solution of water in FA 1.18 [17], 1.17 [18] kJ mol⁻¹.

Excess volumes of mixtures of FA with methanol and water are negative, i.e. mixtures occupy smaller volume than in ideal state. But the methanol–formamide system is considerably more deviated from ideal behaviour on magnitude of excess volume than the water–formamide system. So, the excess volume equals −0.55 sm³ mol⁻¹ [3, 6] for equimolar composition in the first case, in the second one V ^E = −0.13 sm³ mol⁻¹ (our calculation from the data [10]) at 298.15 K. It is interesting to note the excess volume of ethylene glycol–formamide mixture has an opposite sign and equals 0.06 sm³ mol⁻¹ for equimolar composition according to our calculation from the data [9]. Thus, within a given criteria these mixtures can be ranged by the degree of non-ideality: methanol–FA > water–FA > ethylene glycol–FA.

De Visser and Somsen in [19] have studied Bu₄NBr in the series of amides at 278.15–328.15 K by a calorimetric method. Then they [20] have investigated the solutions of Bu₄NBr in binary mixtures containing water, FA, N-methylformamide and DMFA at 298.15 K.

The authors of work [21] have studied the solutions of TAA salts in mixtures FA and HMPT with water at 298.15 or 328.15 K by a calorimetric method. This paper has been limited on an interval of compositions (X ≤ 0.125 m.f. of amide).

We [22] have reported the enthalpy characteristics of Et₄NBr and Bu₄NBr in MeOH, FA and EG at 298.15 and 313.15 K. Then we [23] have added the data of the solution enthalpies of Hex₄NBr in the same solvents at the same temperatures.

The solutions of Et₄NBr in mixtures water–FA and MeOH–FA have been studied in [24] at 298.15 and 313.15 K.

The thermal characteristics of solutions Bu₄NBr in binary mixtures MeOH–FA and EG–FA in all intervals of mixed solvent have been investigated in [12]. Measurements were limited to one temperature (298.15 K).

Therefore in continuation of previous thermochemical studies it was of interest to receive new thermochemical characteristics of tetrabutylammonium bromide solutions in all intervals of compositions of methanol–formamide and ethylene glycol–formamide mixtures at several temperatures and compare the thermal properties of these mixtures with available data in the literature. Also the aim of this work was the obtaining of the standard enthalpies of solution of Bu₄NBr in binary mixtures and the comparison with the data received by the different methods of extrapolation.

Experimental

Materials

Tetrabutylammonium bromide (Merck) was dried under reduced pressure at 343.15 K for 72 h and used without further purification. Formamide «Reachem (pure)» was frozen, dried with molecular sieves 3 Å and twice distillated under reduced pressure at 348.15 K. Fisher titration indicated the presence of 0.04 mass% water in formamide. Methanol «HPLC grade Fisher Scientific 99.99%» and ethylene glycol «Sigma–Aldrich spectrophotometric grade 99+%» with water content <0.01% were used without further purification.

Solution calorimetry

The enthalpies of solution have been measured on an automated isoperibol calorimeter provided with a 60-sm³ titanum vessel. The construction of a calorimeter and test of its work were considered in detail earlier [23, 25]. A comparative method has been used for the measurement of heat effects. The calibration of the system by an electric current was carried out before each experiment. Mixtures have been prepared by weighing the liquids in ground stoppered bottles taking due precautions to minimize the evaporation losses for slightly volatile MeOH and to penetrate the moisture for hygroscopic EG and FA. All the weighing was performed by means of an electronic analytical balance (OKB Vesta) with accuracy 1 mg. The uncertainty in the mole fraction is estimated to be lower than ±2 10⁻⁴.

Results

The integral enthalpies of solution Δ_sol H ^m of Bu₄NBr in mixed solvents in methanol–formamide and ethylene glycol–formamide mixed solvents at 313.15 K are listed in Table 1.

Table 1 The integral enthalpies of solution (∆_sol H ^m/kJ mol⁻¹) of Bu₄NBr in mixtures of formamide with methanol and ethylene glycol and the appropriate Debye–Hückel limiting law slope (A _H/kJ kg^1/2 mol^−3/2) at 313.15 K

The dependence of the integral enthalpies of solution of electrolyte on concentration in any solvent can be represented by Redlich–Rosenfeld–Meyer type equation [26]:

$$ \Updelta_{\text{sol}} H^{m} = \Updelta_{\text{sol}} H^{0} + A_{\rm H} m^{1/2} + B\,m $$

(1)

where A _H is the appropriate Debye–Hückel limiting law slope and B is the empirical constant varying with electrolyte, solvent and temperature. For a given solvent at a given temperature, A _H is constant for all electrolytes with the identical charge.

$$ A_{\text{H}} = - \left( {\nu /2} \right)^{1/2} \,\cdot\, \left| {z_{ + } z_{ - } } \right|^{3/2} \,\cdot \,\nu \,\cdot \,{\hbox{RT}}^{2} \,\cdot\, A \,\cdot\, \left( {{\frac{1}{T}} + {\frac{{\partial { \ln }\varepsilon }}{\partial T}} + {\frac{\alpha }{3}}} \right) $$

(2)

where ν is the number of ions of charge z _i per “molecule” of electrolyte.

The term A can be written as follows:

$$ A = \sqrt {{\frac{{2\pi N_{A} \cdot e^{6} \rho }}{{1000(\varepsilon \cdot kT)^{3} }}}} = {\frac{{4.201 \cdot 10^{6} \rho^{1/2} }}{{(\varepsilon T)^{3/2} }}} $$

(3)

where ρ and ε are the density and the dielectric constant of pure or mixed solvent. Other symbols have their usual meanings [27].

Reliable calculation of the numerical values of A _H requires proper physicochemical data. The data for investigated binary mixtures necessary for calculation are limited. There are only data of the density for the formamide–methanol system at the different temperatures [6]. The data on the electric permittivity ε of studied mixtures is not found by us even at the one temperature. In such cases it is necessary to use those or other additive schemes.

The expression for molar volume of the mixture containing formamide and component S (MeOH, EG) is written as:

$$ V = X_{\text{FA}} \,V_{\text{FA}} + X_{S} \,V_{S} + V^{E} $$

(4)

where X _FA, X _S is the mole fractions of FA and co-solvent, respectively, V _FA, V _S is their molar volumes, V ^E is the excess volume of mixed solvent.

Density of mixture is calculated by Eq. 5:

$$ \rho = {\frac{{X_{\text{FA}} M_{\text{FA}} + X_{S} M_{S} }}{{X_{\text{FA}} V_{\text{FA}} + X_{S} V_{S} + V^{E} }}} $$

(5)

where M _FA, M _S is the molar masses.

For ideal mixture the density can be written as:

$$ \rho^{\text{id}} = {\frac{{X_{\text{FA}} M_{\text{FA}} + X_{S} M_{S} }}{{X_{\text{FA}} V_{\text{FA}} + X_{S} V_{S} }}} $$

(6)

Thermal expansibility coefficient of mixed solvent is calculated by the equation:

$$ \alpha = - {{\frac{1}{\rho }}}\,{{\frac{\partial \rho }{\partial T}}} = {{\frac{1}{V}}}\,{{\frac{\partial V}{\partial T}}} = {\frac{{\alpha_{\text{FA}} X_{\text{FA}} V_{\text{FA}} + \alpha_{S} X_{S} V_{S} + \partial V^{E} /\partial T}}{{X_{\text{FA}} V_{\text{FA}} + X_{S} V_{S} + V^{E} }}} $$

(7)

The neglecting of the term ∂V ^E/∂T brings the greatest uncertainty in the α value. The ignoring of the term V ^E in the denominator is received:

$$ \alpha = \varphi_{\text{FA}} \alpha_{\text{FA}} + \varphi_{S} \alpha_{S} + {\frac{{\partial V^{E} /\partial T}}{{X_{\text{FA}} V_{\text{FA}} + X_{S} V_{S} }}} $$

(8)

where φ_FA, φ _S is the volume fractions, determined by Eq. 9:

$$ \varphi_{\text{FA}} = {\frac{{X_{\text{FA}} V_{\text{FA}} }}{{X_{\text{FA}} V_{\text{FA}} + X_{S} V_{S} }}},\,\varphi_{S} = {\frac{{X_{S} V_{S} }}{{X_{\text{FA}} V_{\text{FA}} + X_{S} V_{S} }}} $$

(9)

For an ideal mixture it is received:

$$ \alpha^{\text{id}} = \varphi_{\text{FA}} \alpha_{\text{FA}} + \varphi_{S} \alpha_{S} $$

(10)

Because of the absence of the data of V ^E and ∂V ^E/∂T for EG–FA the values of α are calculated by the Eq. 10.

The values of electrical permittivity ε of mixtures are defined using the equation offered in the present work:

$$ { \ln }\varepsilon = \varphi_{\text{FA}} { \ln }\varepsilon_{\text{FA}} + \varphi_{S} { \ln }\varepsilon_{S} $$

(11)

Differentiating expression (11) is received:

$$ {\frac{{\partial { \ln }\varepsilon }}{\partial T}} = \varphi_{\text{FA}} {\frac{{\partial { \ln }\varepsilon_{\text{FA}} }}{\partial T}} + \varphi_{S} {\frac{{\partial { \ln }\varepsilon_{S} }}{\partial T}} + \varphi_{\text{FA}} \varphi_{S} \left( {\alpha_{S} - \alpha_{\text{FA}} } \right)\left( {{ \ln }\varepsilon_{S} - { \ln }\varepsilon_{\text{FA}} } \right) $$

(12)

The values A, A _H and also parameters required for their calculation for pure solvents at 298.15 and 313.15 K are listed in Table 2, taken from [23]. The values A _H for mixed solvents are listed in Table 1. The values A _H for the studied mixtures in all intervals of compositions of mixed solvent at 298.15 K are presented in Fig. 1.

Table 2 Properties of pure solvents [23]

Fig. 1

The appropriate Debye–Hückel limiting law slope A _H of formamide–methanol (1) and formamide–ethylene glycol (2) mixed solvents at 298.15 K. Lines—Eq. 13

The appropriate Debye–Hückel limiting law slope for mixture may be written as:

$$ A_{\rm H} = X_{\text{FA}} \,A_{{\rm {H}({\text{FA}})}} + X_{S} A_{\rm{H}(S)} + \Updelta A_{\rm H} $$

(13)

The value ∆A _H is the deviation from additivity. The values of ∆A _H for binary mixtures of FA with MeOH and EG were approximated by Redlich–Kister type equation, usually applicable for describing excess functions of binary mixtures:

$$ \Updelta A_{\rm H} = X_{\text{FA}} \,X_{S} (a + b\;X_{FA} ) $$

(14)

where a and b are coefficients presented in Table 3.

Table 3 Coefficients a and b of Eq. 14

The Eq. 13 can be used for calculation of the values of A _H of any uni-univalent electrolytes in the mixtures of FA with MeOH and EG at appropriate temperatures.

Discussion

There is a possibility to compare the two variants of the calculation A _H for FA–MeOH system. For example, for X _FA = 0.4582 m.f. at 298.15 K ∆_sol H ^m = 17.05 kJ mol⁻¹ at m = 0.00488 mol kg⁻¹, ∆_sol H ^m = 17.13 kJ mol⁻¹ at m = 0.0140 mol kg⁻¹ [12]:

$$ \alpha = 8.71\;10^{ - 4} {\text{K}}^{ - 1} ({\text{Eq}}.\;8),\;A_{\rm H} = 3.18\;{\text{kJ}}\;{\text{kg}}^{1/2} \;{\text{mol}}^{ - 3/2} ,\;\Updelta_{\text{sol}} H^{0} = 16.87\;{\text{kJ}}\;{\text{mol}}^{ - 1} ; $$

$$ \alpha^{\text{id}} = 9.97\;10^{ - 4} {\text{K}}^{ - 1} ({\text{Eq}}.\;10),\;A_{\rm H} = 3.07\;{\text{kJ}}\;{\text{kg}}^{1/2} \;{\text{mol}}^{ - 3/2} ,\;\Updelta_{\text{sol}} H^{0} = 16.86\;{\text{kJ}}\;{\text{mol}}^{ - 1} . $$

It is obviously that the using of coefficient of the thermal expansion calculated by the additive scheme is quite admissible for calculation A _H in non-aqueous mixtures (Eq. 10). The curves Δ_sol H ^m vs. m ^1/2 for the investigated salts are presented in Fig. 2. The Δ_sol H ⁰ values for two different temperatures calculated by Eq. 1 are given in Tables 4 and 5. The comparison of the previously received values with the data [12] where the values Δ_sol H ⁰ were calculated in terms of Debye–Hückel theory in the second approximation [28] is presented at 298.15 K in Fig. 3. The values of Δ_sol H ⁰ extrapolated by various methods differ on 1.5% as much as possible.

Fig. 2

The integral enthalpies of solution of Bu₄NBr vs. molality of salt. Mixed solvent formamide–methanol: 1—0.0514, 2—0.0484, 3—0.2461 m.f. of FA. Mixed solvent formamide–ethylene glycol: 4—0.2420, 5—0.1926 m.f. of FA. Temperatures: 1, 4, 5—298.15; 2, 3—313.15 K. Lines—Eq. 1

Table 4 The standard enthalpies of solution (∆_sol H ⁰/kJ mol⁻¹) of Bu₄NBr in methanol–formamide mixtures at 298.15 and 313.15 K

Table 5 The standard enthalpies of solution (∆_sol H ⁰, kJ mol⁻¹) of Bu₄NBr in ethylene glycol–formamide mixtures at 298.15 and 313.15 K

Fig. 3

The enthalpies of solution of Bu₄NBr vs. composition of mixed solvents formamide–methanol (1, 2) and formamide–ethylene glycol (3, 4) at 298.15 K. 1, 4—[12]; 2, 3—the present work

The enthalpies of transfer of Bu₄NBr from formamide to its mixtures with co-solvents (S) have been calculated as follow:

$$ \Updelta_{\text{tr}} H^{0} ({\text{FA}} \to {\text{FA}} + S) = \Updelta_{\text{sol}} H^{0} ({\text{FA}} + S) - \Updelta_{\text{sol}} H^{0} ({\text{FA}}) $$

(15)

The enthalpies of transfer of Bu₄NBr from formamide to its mixtures with the studied solvents at 298.15 K are given in Fig. 4. Also, the data from [20] for mixtures of FA–water, FA–N-MFA and FA–DMFA are presented here for comparison. As is seen from Fig. 4 additions of co-solvents to formamide influence the enthalpic component of Gibbs energy of the mixed solvent differently. So, addition of ethylene glycol and N-MFA weakens, of methanol practically does not change, and of water and DMFA strengthen solvation of the salt in mixture in comparison with pure formamide. The greatest changes of the transfer enthalpy characteristics of model solvophobic substance Bu₄NBr are observed in system FA–water.

Fig. 4

The enthalpies of transfer of Bu₄NBr from formamide to mixtures of formamide with water (1), dimethylformamide (2), methanol (3), N-methylformamide (4) and ethylene glycol (5) at 298.15 K (see text). Lines are the polynomial description

The heat capacities of solution, $\Updelta C_{p}{^{0}}$, have been determined from the enthalpies of solution by the equation:

$$ \Updelta C_{p}{^{0}} = (\Updelta_{\text{sol}} H^{0} (313.15\;{\text{K}}) - \Updelta_{\text{sol}} H^{0} (298.15\;{\text{K}}))/15 $$

(16)

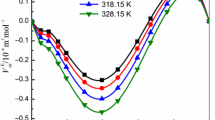
The $\Updelta C_{\text{p}}{^{0}}$ values of Bu₄NBr in formamide–water mixture in investigated temperature interval have been calculated using the data of enthalpies of solution from [20] at 298.15 K and our data at 313.15 K (unpublished results). For this purpose dependences Δ_sol H ⁰ = f(X _FA) have been approximated by polynomials of the conforming power so that the standard deviation s _f did not exceed 0.18 kJ mol⁻¹ in case of H₂O–FA system, s _f ≤ 0.14 kJ mol⁻¹ in EG–FA system and s _f ≤ 0.05 kJ mol⁻¹ for MeOH–FA. The calculated values of the heat capacities of solution are presented in Fig. 5.

Fig. 5

The heat capacities of Bu₄NBr solution in mixtures of formamide with methanol (1), ethylene glycol (2) and water (3) in the 298.15–313.15 K temperature interval

In work [22] it is shown that the solutions of tetraalkylammonium salts in FA have properties similar to those of aqueous rather than methanol solutions. Although solvophobic solvation effects are weaker than those in water they are possible in FA. The results obtained allow the solvent studied to be arranged as: H₂O > FA > EG > MeOH in order of weakening of solvophobic solvation effects [22]. The same sequence of individual solvents studied is shown in Fig. 5 in order of decreasing of the $\Updelta C_{\text{p}}{^{0}}$ value.

The value of $\Updelta C_{\text{p}}{^{0}}$ in water is positive and large enough and the first additions of FA (X _FA <0.3 m.f.) result in to its sharp decrease (Fig. 5). It is possible to assume the fragments of the own structure of water are conserved in this area. And the own structure of formamide is formed in the field of a mixed solvent X _FA ≥ 0.3 m.f. The additions of amide to MeOH and EG result in inconsiderable growth of $\Updelta C_{\text{p}}{^{0}}$ values on over the range of the mixed solvent. The heat capacities of Bu₄NBr solution in ethylene glycol and methanol systems in the region of X _FA ≥ 0.5 m.f. become practically identical. The presence of the own structure of water in the region of small additions of formamide considerably distinguishes the H₂O–FA system from the investigated non-aqueous systems.

It is interesting to consider a deviation from additivity of the $\Updelta C_{\text{p}}{^{0}}$ value for aqueous and non-aqueous systems containing formamide (Fig. 6). The $\Updelta C_{\text{p}}{^{0}}$ values were computed by Redlich–Kister type equations of the conforming powers. In aqueous system of formamide the deviation values are negative and very great. And for non-aqueous systems of formamide the values of deviation are practically equal and positive.

Fig. 6

The values of $\Updelta \Updelta C_{\text{p}}{^{0}}$ of Bu₄NBr vs. composition of mixtures of formamide with methanol (1), ethylene glycol (2) and water (3). Lines are the description by the Redlich–Kister type equations

Thus it is reasonable to guess that the appearance of the own structure of water in X _FA < 0.3 m.f. is responsible for essential different behaviour of electrolyte in the region of small additions of FA to water and non-aqueous solvents.

Conclusions

The heats of solution of Bu₄NBr have been measured in mixtures of formamide with methanol and ethylene glycol at 313.15 K by calorimetric method for the first time.

The standard enthalpies of solution in binary mixtures have been extrapolated to infinite dilution by Redlich–Rosenfeld–Meyer type equation using the literary data at 298.15 K and the present paper data at 313.15 K.

The Debye–Hückel limiting law slope A _H required for calculation of the Δ_sol H ⁰ value has been obtained with application the new additive scheme of determination of the physico-chemical characteristics of binaries. The scheme is tested on the example of Bu₄NBr solutions in FA–MeOH mixture at 298.15 K. Its application yields the Δ_sol H ⁰ value very closed on the ones determined with the real (non-additive) characteristics of binaries.

The standard enthalpies of solution extrapolated by Redlich–Rosenfeld–Meyer type equation are in a good agreement with the ones computed in terms of the Debye–Hückel theory in the second approximation.

The heat capacities characteristics of Bu₄NBr have been calculated in H₂O–FA, MeOH–FA and EG–FA mixtures using the literary and present data. The sequence of solvents H₂O > FA > EG > MeOH located on their ability to solvophobic solvation found by us earlier for enthalpic characteristics is confirmed by the $\Updelta C_{\text{p}}{^{0}}$ values.

The investigations carried out allow revealing the important differences in behaviour of hydrophobic electrolyte Bu₄NBr in mixtures of formamide with water, methanol and ethylene glycol. It is found that the presence of the own structure of water in the region of small additions of formamide to co-solvents considerably differs the H₂O–FA system from investigated non-aqueous systems. Some common features of behaviour of Bu₄NBr in formamide mixtures with water, methanol and ethylene glycol occur only in the region rich enough in formamide content (X _FA > 0.7 m.f.).