A Bayesian method with empirically fitted priors for the evaluation of environmental radioactivity: application to low-level radioxenon measurements

Abstract

The decision that a given detection level corresponds to the effective presence of a radionuclide is still widely made on the basis of a classic hypothesis test. However, the classic framework suffers several drawbacks, such as the conceptual and practical impossibility to provide a probability of zero radioactivity, and confidence intervals for the true activity level that are likely to contain negative and hence meaningless values. The Bayesian framework being potentially able to overcome these drawbacks, several attempts have recently been made to apply it to this decision problem. Here, we present a new Bayesian method that, unlike the previous ones, presents two major advantages together. First, it provides an estimate of the probability of no radioactivity, as well as physically meaningful point and interval estimates for the true radioactivity level. Second, whereas Bayesian approaches are often controversial because of the arbitrary choice of the priors they use, the proposed method permits to estimate the parameters of the prior density of radioactivity by fitting its marginal distribution to previously recorded activity data. The new scheme is first mathematically developed. Then, it is applied to the detection of radioxenon isotopes in noble gas measurement stations of the International Monitoring System of the Comprehensive Nuclear-Test-Ban Treaty.

Appendix: Bayesian estimates for the proposed priors

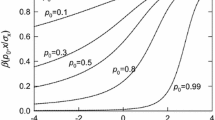
In order to lighten the notations, the a priori probability of zero activity P(H ₀) is denoted by p ₀ in the following results. According to (6), since f(x|μ) = 1/σ φ((x − μ)/σ), the a posteriori probability of H ₀ is always of the form:

$$ P(H_{0} |x) = \frac{{\frac{{p_{0} }}{\sigma }\varphi \left( {\frac{x}{\sigma }} \right)}}{f(x)} $$

(17)

According to (7), the posterior density of μ is always of the form:

$$ f(\mu |x) = P(H_{0} |x)\delta_{0} (\mu ) + (1 - p_{0} )\frac{{\pi (\mu |H_{1} )}}{f(x)}\frac{1}{\sigma }\varphi \left( {\frac{x - \mu }{\sigma }} \right) $$

(18)

The marginal density f(x), the Bayesian point estimate (8), and the credibility interval (9) for μ are given below for the three priors.

Uniform prior

With the uniform prior (13), the marginal density is given by:

$$ f(x) = \frac{{p_{0} }}{\sigma }\varphi \left( {\frac{x}{\sigma }} \right) + \frac{{1 - p_{0} }}{d}\left( {\Upphi \left( {\frac{x}{\sigma }} \right) - \Upphi \left( {\frac{x - d}{\sigma }} \right)} \right) $$

(19)

Bayesian point estimate:

$$ \mu^{*} = \frac{{\sigma (1 - p_{0} )}}{d \times f(x)}\left( {\varphi \left( {\frac{x}{\sigma }} \right) - \varphi \left( {\frac{x - d}{\sigma }} \right)} \right) + x\left( {\Upphi \left( {\frac{x}{\sigma }} \right) - \Upphi \left( {\frac{x - d}{\sigma }} \right)} \right) $$

(20)

1 − γ credibility interval:

$$ \left\{ \begin{gathered} \mu^{ + } = x + \sigma \times \Upphi^{ - 1} \left( {\Upphi \left( {\frac{d - x}{\sigma }} \right) - \frac{\gamma }{2}\frac{d \times f(x)}{{1 - p_{0} }}} \right) \\ \mu^{ - } = x + \sigma \times \Upphi^{ - 1} \left( {\Upphi \left( {\frac{d - x}{\sigma }} \right) - \left( {1 - \frac{\gamma }{2}} \right)\frac{d \times f(x)}{{1 - p_{0} }}} \right) \, {\text{if}} \, P(H_{0} |x) < \frac{\gamma }{2},\,{\text{else}}\,\mu^{ - } = 0 \\ \end{gathered} \right. $$

(21)

Exponential prior

Marginal density with the exponential prior (14):

$$ f(x) = \frac{{p_{0} }}{\sigma }\varphi \left( {\frac{x}{\sigma }} \right) + \frac{{1 - p_{0} }}{\tau }\exp \left( {\frac{{\sigma^{2} }}{{2\tau^{2} }} - \frac{x}{\tau }} \right)\Upphi \left( {\frac{{x - \frac{{\sigma^{2} }}{\tau }}}{\sigma }} \right) $$

(22)

Bayesian point estimate:

$$ \mu^{*} = \frac{{(1 - p_{0} )}}{\sigma \times \tau }\frac{{\exp \left( {\frac{{\sigma^{2} }}{{2\tau^{2} }} - \frac{x}{\tau }} \right)}}{f(x)}\left( {\sigma^{2} \varphi \left( {\frac{{x - \frac{{\sigma^{2} }}{\tau }}}{\sigma }} \right) + \left( {x - \frac{{\sigma^{2} }}{\tau }} \right)\Upphi \left( {\frac{{x - \frac{{\sigma^{2} }}{\tau }}}{\sigma }} \right)} \right) $$

(23)

1 − γ credibility interval:

$$ \left\{ \begin{gathered} \mu^{ + } = x - \frac{{\sigma^{2} }}{\tau } + \sigma \times \Upphi^{ - 1} \left( {1 - \frac{\gamma }{2}\frac{\tau \times f(x)}{{1 - p_{0} }}\exp \left( {\frac{x}{\tau } - \frac{{\sigma^{2} }}{{2\tau^{2} }}} \right)} \right) \hfill \\ \mu^{ - } = x - \frac{{\sigma^{2} }}{\tau } + \sigma \times \Upphi^{ - 1} \left( {1 - \left( {1 - \frac{\gamma }{2}} \right)\frac{\tau \times f(x)}{{1 - p_{0} }}\exp \left( {\frac{x}{\tau } - \frac{{\sigma^{2} }}{{2\tau^{2} }}} \right)} \right){\text{ if}}\,P(H_{0} |x) < \frac{\gamma }{2},\,{\text{else }}\mu^{ - } = 0 \hfill \\ \end{gathered} \right. $$

(24)

Half-Gaussian prior

Let us define ω according to:

$$ \frac{1}{{\omega^{2} }} = \frac{1}{{\lambda^{2} }} + \frac{1}{{\sigma^{2} }} $$

Marginal density with the half-Gaussian prior (15):

$$ f(x) = \frac{{p_{0} }}{\sigma }\varphi \left( {\frac{x}{\sigma }} \right) + \frac{{(1 - p_{0} )2\omega }}{\sigma \lambda }\varphi \left( {\frac{x}{\lambda }} \right)\Upphi \left( {\frac{\omega }{{\sigma^{2} }}x} \right) $$

(25)

Bayesian point estimate:

$$ \mu^{*} = \frac{{2(1 - p_{0} )}}{\lambda \sigma f(x)}\varphi \left( {\frac{x}{\lambda }} \right)\left( {\frac{{\omega^{3} x}}{{\sigma^{2} }}\Upphi \left( {\frac{\omega x}{{\sigma^{2} }}} \right) + \omega^{2} \varphi \left( {\frac{\omega x}{{\sigma^{2} }}} \right)} \right) $$

(26)

1 − γ credibility interval:

$$ \left\{ \begin{array}{ll} \mu^{ + } = \frac{{\omega^{2} }}{{\sigma^{2} }}x + \omega \times \Upphi^{ - 1} \left( {1 - \frac{\gamma }{2}\frac{\lambda \times \sigma \times f(x)}{{2\omega (1 - p_{0} )\varphi \left( {x/\lambda } \right)}}} \right) \\ {\mu^{ - }}= \frac{{\omega^{2} }}{{\sigma^{2} }}x + \omega \times \Upphi^{ - 1} \left( {1 - \left( {1 - \,\frac{\gamma }{2}} \right)\frac{\lambda \times \sigma \times f(x)}{{2\omega (1 - p_{0} )\varphi \left( {x/\lambda } \right)}}} \right){\text{ if }}P(H_{0} |x) < \gamma /2,{\text{ else }}{\mu^{ - }} = 0 \\ \end{array} \right. $$

(27)