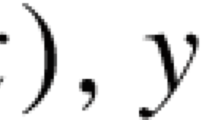Abstract
The Bregman-function-based Proximal Point Algorithm for variational inequalities is studied. Classical papers on this method deal with the assumption that the operator of the variational inequality is monotone. Motivated by the fact that this assumption can be considered to be restrictive, e.g., in the discussion of Nash equilibrium problems, the main objective of the present paper is to provide a convergence analysis only using a weaker assumption called quasimonotonicity. To the best of our knowledge, this is the first algorithm established for this general and frequently studied class of problems.

Similar content being viewed by others
Notes
That is, \(\mathcal {T}\) is the (sub)differential of a quasiconvex function (whose required analytical properties are tacitly assumed to hold here).
Single-valued operators \(\mathcal {T}: \mathbb {R}^{n} \to \mathbb {R}^{n}\) are included in the canonical way.
Although a large class of linearly and nonlinearly constrained sets admits the existence of such a function, it is worthy of mention that there are still some sets K for which the existence of a zone-coercive Bregman-like function (with zone \(\operatorname{int} K\)) is still unknown (see [2, Example 3] and [23] in this regard).
There are some more examples in which this property holds, but the case of strongly convex h is enough for the present paper.
The latter assumption might be considered as a critical one; some related comments are postponed to the discussion of all assumptions made in the convergence analysis below.
For example, in case \(\mathcal {T}\) is single-valued, we might think of Newton-type methods, etc.
Of course, if relative errors are left out by letting σ=0, we obtain y k=x k+1, and thus no such extragradient-like step is necessary.
This will be concretized below, but for instance, it is sufficient that they tend to zero.
Of course, a suitable parameter choice, regularity conditions, etc. are also necessary, but this falls out of the scope of the present discussion.
It is rather easy to see that this property is not necessary if ∇h is Lipschitz continuous (as is the case, e.g., within classical proximal point methods). As Lipschitz continuity of ∇h contradicts the zone coerciveness of h, one might consider this assumption as the price to pay for unconstrained subproblems.
For the sake of simplicity, we leave out technical details here and reduce ourselves to a very pregnant formulation. This also includes that the exact version of the BPPA is dealt with, i.e., there is only one generated sequence that may converge or not.
Anyway, it should be noted that this construction describes the only known Bregman-like functions with a nonlinearly constrained zone.
In fact, this makes the assumption of the existence of nonzero solutions superfluous.
References
Burachik, R., Iusem, A.: A generalized Proximal Point Algorithm for the variational inequality problem in a Hilbert space. SIAM J. Optim. 8, 197–216 (1998)
Langenberg, N.: Pseudomonotone operators and the Bregman Proximal Point Algorithm. J. Glob. Optim. 47, 537–555 (2010)
Langenberg, N., Tichatschke, R.: Interior proximal methods for quasiconvex optimization. J. Glob. Optim. 52, 641–661 (2012)
Aussel, D., Corvellec, J.N., Lassonde, M.: Subdifferential characterization of quasiconvexity and convexity. J. Convex Anal. 1, 195–201 (1994)
Hadjisavvas, N., Schaible, S.: Quasimonotone variational inequalities in Banach spaces. J. Optim. Theory Appl. 90, 95–111 (1996)
Aussel, D., Hadjisavvas, N.: Technical note: on quasimonotone variational inequalities. J. Optim. Theory Appl. 121, 445–450 (2004)
Konnov, I.: On quasimonotone variational inequalities. J. Optim. Theory Appl. 99, 165–181 (1998)
Karamardian, S., Schaible, S.: Seven kinds of monotone maps. J. Optim. Theory Appl. 66, 37–46 (1990)
Karamardian, S., Schaible, S., Crouzeix, J.P.: Characterizations of generalized monotone maps. J. Optim. Theory Appl. 76, 399–413 (1993)
Crouzeix, J.P., Ferland, J.: Criteria for differentiable generalized monotone maps. Math. Program. 75, 399–406 (1996)
Hadjisavvas, N., Komlosi, S., Schaible, S. (eds.): Handbook of Generalized Convexity and Generalized Monotonicity. Nonconvex Optimization and Its Applications, vol. 76. Springer, Boston (2005)
Polyak, B.T.: Introduction to Optimization. Optimization Software, New York (1987)
Facchinei, F., Pang, J.S.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer, New York (2003)
Crouzeix, J.P., Eberhard, A., Ralph, D.: A geometrical insight on pseudoconvexity and pseudomonotonicity. Math. Program. 123, 61–83 (2010)
Karamardian, S.: Complementarity problems over cones with monotone and pseudomonotone maps. J. Optim. Theory Appl. 18, 445–454 (1976)
Rockafellar, R., Wets, R.: Variational Analysis. Springer, Berlin (1997)
Bauschke, H., Borwein, J.: Legendre functions and the method of random Bregman projections. J. Convex Anal. 4, 27–67 (1997)
Bregman, L.: The relaxation method of finding the common points of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 7, 200–217 (1967)
Censor, Y., Zenios, S.: Proximal minimization algorithm with D-functions. J. Optim. Theory Appl. 73, 451–464 (1992)
Chen, G., Teboulle, M.: Convergence analysis of a proximal-like minimization algorithm using Bregman functions. SIAM J. Optim. 3, 538–543 (1993)
Eckstein, J.: Nonlinear proximal point algorithms using Bregman functions, with application to convex programming. Math. Oper. Res. 18, 202–226 (1993)
Censor, Y., Iusem, A., Zenios, S.: An interior point method with Bregman functions for the variational inequality problem with paramonotone operators. Math. Program. 81, 373–400 (1998)
Kaplan, A., Tichatschke, R.: Note on the paper: interior proximal method for variational inequalities on non-polyhedral sets. Discuss. Math., Differ. Incl. Control Optim. 30, 51–59 (2010)
Solodov, M., Svaiter, B.: An inexact hybrid generalized Proximal Point Algorithm and some new results on the theory of Bregman functions. Math. Oper. Res. 25, 214–230 (2000)
Kaplan, A., Tichatschke, R.: On inexact generalized proximal methods with a weakened error tolerance criterion. Optimization 53, 3–17 (2004)
Eckstein, J.: Approximate iterations in Bregman-function-based proximal algorithms. Math. Program. 83, 113–123 (1998)
Han, D.: A new hybrid generalized Proximal Point Algorithm for variational inequality problems. J. Glob. Optim. 26, 125–140 (2003)
Langenberg, N.: Convergence Analysis of Proximal-Like Methods for Variational Inequalities and Fixed Point Problems Applications to the Nash Equilibrium Problem. Logos, Berlin (2011)
Langenberg, N.: Convergence analysis of an extended Auxiliary Problem Principle with various stopping criteria. Optim. Methods Softw. 26, 127–154 (2011)
Langenberg, N.: On the cutting plane property and the Bregman Proximal Point Algorithm. J. Convex Anal. 18, 601–619 (2011)
Crouzeix, J.P., Marcotte, P., Zhu, D.: Conditions ensuring the applicability of cutting plane methods for solving variational inequalities. Math. Program. 88, 521–539 (2000)
Castellani, M., Giuli, M.: A characterization of the solution set of pseudoconvex extremum problems. J. Convex Anal. 19 (2013)
Kaplan, A., Tichatschke, R.: Interior proximal method for variational inequalities: case of non-paramonotone operators. Set-Valued Anal. 12, 357–382 (2004)
Burachik, R., Dutta, J.: Inexact proximal point methods for variational inequality problems. SIAM J. Optim. 20, 2653–2678 (2010)
Acknowledgements
I am grateful to an anonymous referee whose comments greatly improved the present paper. Moreover, my thanks also go to the associate editor and the editor-in-chief for further very helpful remarks.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Nicolas Hadjisavvas.
Rights and permissions
About this article
Cite this article
Langenberg, N. An Interior Proximal Method for a Class of Quasimonotone Variational Inequalities. J Optim Theory Appl 155, 902–922 (2012). https://doi.org/10.1007/s10957-012-0111-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-012-0111-9