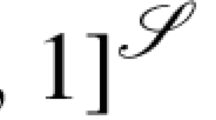Abstract
In the Sherrington–Kirkpatrick (SK) and related mixed p-spin models, there is interest in understanding replica symmetry breaking at low temperatures. For this reason, the so-called AT line proposed by de Almeida and Thouless as a sufficient (and conjecturally necessary) condition for symmetry breaking, has been a frequent object of study in spin glass theory. In this paper, we consider the analogous condition for the multi-species SK model, which concerns the eigenvectors of a Hessian matrix. The analysis is tractable in the two-species case with positive definite variance structure, for which we derive an explicit AT temperature threshold. To our knowledge, this is the first non-asymptotic symmetry breaking condition produced for a multi-species spin glass. As possible evidence that the condition is sharp, we draw further parallel with the classical SK model and show coincidence with a separate temperature inequality guaranteeing uniqueness of the replica symmetric critical point.
Similar content being viewed by others
References
Agliari, E., Barra, A., Galluzzi, A., Guerra, F., Moauro, F.: Multitasking associative networks. Phys. Rev. Lett. 109, 1–5 (2012)
Agliari, E., Barra, A., Guerra, F., Moauro, F., Agliari, E., Barra, A., Guerra, F., Moauro, F.: A thermodynamic perspective of immune capabilities. J. Theor. Biol. 287, 48–63 (2011)
Aizenman, M., Lebowitz, J.L., Ruelle, D.: Some rigorous results on the Sherrington–Kirkpatrick spin glass model. Commun. Math. Phys. 112(1), 3–20 (1987)
Amit, D.J., Gutfreund, H., Sompolinsky, H.: Spin-glass models of neural networks. Phys. Rev. A 32(2), 1007–1018 (1985)
Auffinger, A., Chen, W.-K.: On properties of Parisi measures. Probab. Theory Relat. Fields 161(3–4), 817–850 (2015)
Auffinger, A., Chen, W.-K.: The Parisi formula has a unique minimizer. Commun. Math. Phys. 335(3), 1429–1444 (2015)
Auffinger, A., Chen, W.-K., Zeng, Q.: The SK model is full-step replica symmetry breaking at zero temperature. Preprint, available at arXiv:1703.06872
Barra, A., Agliari, E.: A statistical mechanics approach to autopoietic immune networks. J. Stat Mech. Theory E 2010(07), 1–24 (2010)
Barra, A., Agliari, E.: A statistical mechanics approach to Granovetter theory. Phys. A 391(10), 3017–3026 (2012)
Barra, A., Contucci, P.: Toward a quantitative approach to migrants integration. Europhys. Lett. 89(6), 1–6 (2010)
Barra, A., Contucci, P., Mingione, E., Tantari, D.: Multi-species mean field spin glasses. Rigorous results. Ann. Henri Poincaré 16(3), 691–708 (2015)
Barra, A., Galluzzi, A., Pizzoferrato, A., Tantari, D.: Mean field bipartite spin models treated with mechanical techniques. Eur. Phys. J. 87(3), 74 (2014)
Barra, A., Genovese, G., Guerra, F.: The replica symmetric approximation of the analogical neural network. J. Stat. Phys. 140(4), 784–796 (2010)
Barra, A., Genovese, G., Guerra, F.: Equilibrium statistical mechanics of bipartite spin systems. J. Phys. A 44(24), 245002, 22 (2011)
Barra, A., Genovese, G., Guerra, F., Tantari, D.: How glassy are neural networks? J. Stat. Mech. 07, 1–16 (2012)
Barra, A., Guerra, F.: About the ergodic regime in the analogical Hopfield neural networks: moments of the partition function. J. Math. Phys. 49(12), 1–18 (2008)
Bovier, A., Picco, P. (eds.): Mathematical Aspects of Spin Glasses and Neural Networks. Progress in Probability, vol. 41. Birkhäuser Boston Inc, Boston, MA (1998)
Contucci, P., Gallo, I., Menconi, G.: Phase transitions in social sciences: two-population mean field theory. Int. J. Mod. Phys. B 22(14), 2199–2212 (2008)
Contucci, P., Ghirlanda, S.: Modeling society with statistical mechanics: an application to cultural contact and immigration. Qual. Quant. 41(4), 569–578 (2007)
de Almeida, J.R.L., Thouless, D.J.: Stability of the Sherrington–Kirkpatrick solution of a spin glass model. J. Phys. A 11(5), 983–990 (1978)
Edwards, S.F., Anderson, P.W.: Theory of spin glasses. J. Phys. F 5(5), 965–974 (1975)
Fedele, M., Contucci, P.: Scaling limits for multi-species statistical mechanics mean-field models. J. Stat. Phys. 144(6), 1186–1205 (2011)
Fedele, M., Unguendoli, F.: Rigorous results on the bipartite mean-field model. J. Phys. A 45(38), 385001, 18 (2012)
Gallo, I., Contucci, P.: Bipartite mean field spin systems. Existence and solution. Math. Phys. Electron. J. 14 (2008), Paper 1, 21
Guerra, F.: Sum, rules for the free energy in the mean field spin glass model. In: Mathematical physics in mathematics and physics (Siena, : vol. 30 of Fields Institute Communications American Mathematical Society. Providence, RI, 2001), 161–170 (2000)
Guerra, F., Toninelli, F.L.: Quadratic replica coupling in the Sherrington–Kirkpatrick mean field spin glass model. J. Math. Phys. 43(7), 3704–3716 (2002)
Guerra, F., Toninelli, F.L.: The thermodynamic limit in mean field spin glass models. Commun. Math. Phys. 230(1), 71–79 (2002)
Hopfield, J.J.: Neural networks and physical systems with emergent collective computational abilities. Proc. Nat. Acad. Sci. USA 79(8), 2554–2558 (1982)
Jagannath, A., Tobasco, I.: Some properties of the phase diagram for mixed \(p\)-spin glasses. Probab. Theory Relat. Fields 167(3–4), 615–672 (2017)
Krapivsky, P.L., Redner, S.: Dynamics of majority rule in two-state interacting spin systems. Phys. Rev. Lett. 90, 1–4 (2003)
Latała, R.: Exponential inequalities for the SK model of spin glasses, extending Guerras method. Unpublished manuscript (2002)
Mézard, M., Montanari, A.: Information, Physics, and Computation. Oxford Graduate Texts. Oxford University Press, Oxford (2009)
Mézard, M., Parisi, G., Virasoro, M.A.: Spin Glass Theory and beyond. World Scientific Lecture Notes in Physics, vol. 9. World Scientific Publishing Co. Inc., Teaneck (1987)
Nishimori, H.: Statistical physics of spin glasses and information processing, vol. 111 of International Series of Monographs on Physics. Oxford University Press, New York, 2001. An introduction, Translated from the 1999 Japanese original
Panchenko, D.: Free energy in the generalized Sherrington–Kirkpatrick mean field model. Rev. Math. Phys. 17(7), 793–857 (2005)
Panchenko, D.: The Sherrington–Kirkpatrick Model. Springer Monographs in Mathematics. Springer, New York (2013)
Panchenko, D.: The Parisi formula for mixed \(p\)-spin models. Ann. Probab. 42(3), 946–958 (2014)
Panchenko, D.: The free energy in a multi-species Sherrington–Kirkpatrick model. Ann. Probab. 43(6), 3494–3513 (2015)
Parisi, G.: Infinite number of order parameters for spin-glasses. Phys. Rev. Lett. 43, 1754–1756 (1979)
Parisi, G.: A sequence of approximated solutions to the S–K model for spin glasses. J. Phys. A 13(4), L115–L121 (1980)
Parisi, G.: A simple model for the immune network. Proc. Natl. Acad. Sci. USA 87(1), 429–433 (1990)
Sherrington, D., Kirkpatrick, S.: Solvable model of a spin-glass. Phys. Rev. Lett. 35(26), 1792–1796 (1975)
Talagrand, M.: On the high temperature phase of the Sherrington–Kirkpatrick model. Ann. Probab. 30(1), 364–381 (2002)
Talagrand, M.: The Parisi formula. Ann. Math. 163(2), 221–263 (2006)
Talagrand, M.: Mean field models for spin glasses. Volume I, vol. 54 of Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics]. Springer-Verlag, Berlin, 2011. Basic examples
Talagrand, M.: Mean field models for spin glasses. Volume II, vol. 55 of Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics]. Springer, Heidelberg, 2011. Advanced replica-symmetry and low temperature
Toninelli, F.L.: About the Almeida–Thouless transition line in the Sherrington–Kirkpatrick mean-field spin glass model. Europhys. Lett. 60(5), 764–767 (2002)
Acknowledgements
We are grateful to Amir Dembo and Andrea Montanari for their advice and encouragement on this project. We thank Antonio Auffinger, Erwin Bolthausen, and Aukosh Jagannath for their insights and feedback, and the referee for several suggestions to improve the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
E.B. was partially supported by NSF Grant DGE-114747
L.S. was partially supported by NSF Grant DGE-1656518.
A Proof of Lemma 3.1
A Proof of Lemma 3.1
Proof of Lemma 3.1
Here we consider (1.6) when \(k = 1\), and
Recall that with these choices, we have \(Q_0 = Q_0^s = 0\) and
We have
where
In simplifying \(X_2^s\), we have used the fact that for \(\eta \sim \mathcal {N}(0,1)\) and \(\sigma >0\),
In summary,
Notice that when \(\zeta = 1\), we recover the replica symmetric expression (1.9):
Henceforth fix an RS critical point \(q = q_*\in \mathcal {C}(\beta ,h)\). For ease of notation, let us write
so that
We can then calculate
which gives
When \(p = q_*\), we have \(Y_2^s = Y_1^s\) and \(Q_2 = Q_1\). In particular, \(Y_2^s\) has no dependence on \(\eta _2\), and so the above expression reduces to \(V(q_*) = 0\). This proves claim (a).
The next step is to take partial derivatives with respect to the \(p^t\). First, we use (A.1) to make the simple calculation
Since \(Y_1^s\) has no dependence on p, and
we find
Next we observe that for any twice differentiable function whose derivatives have at most exponential growth at infinity, (A.6) and Gaussian integration by parts together give
Hence
We now apply (A.9) to \(f(x) = \log (\cosh x)\cosh x\), for which
to obtain
Finally, we have
Using (A.7), (A.10), and (A.11) in (A.4), we arrive at
Once more, if \(p = q_*\), then \(Y_2^s = Y_1^s\) has no dependence on \(\eta _2\), in which case
Consequently, claim (b) holds: \(\nabla V(q_* ) = 0\).
Our final step is to compute the Hessian of V. We have
where \(\delta _{st^{\prime }} = 1\) if \(s = t^{\prime }\) and 0 zero otherwise. To determine the derivative of the expectation, we apply (A.9) with \(f(x) = \sinh x \tanh x\), for which
After doing so, we arrive at
As before, the expression simplifies when \(p=q^*\), since then \(Y_2^s=Y_1^s\) has no dependence on \(\eta _2\). Namely,
Rewriting the expression in terms of matrices yields claim (c). \(\square \)
Rights and permissions
About this article
Cite this article
Bates, E., Sloman, L. & Sohn, Y. Replica Symmetry Breaking in Multi-species Sherrington–Kirkpatrick Model. J Stat Phys 174, 333–350 (2019). https://doi.org/10.1007/s10955-018-2197-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-018-2197-4