Skip to main content
SpringerLink
Log in

The Shark Random Swim

(Lévy Flight with Memory)

  • Published:
Journal of Statistical Physics Aims and scope Submit manuscript

Abstract

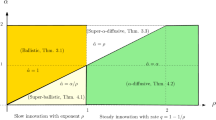
The Elephant Random Walk (ERW), first introduced by Schütz and Trimper (Phys Rev E 70:045101, 2004), is a one-dimensional simple random walk on \( {\mathbb {Z}} \) having a memory about the whole past. We study the Shark Random Swim, a random walk with memory about the whole past, whose steps are \( \alpha \)-stable distributed with \( \alpha \in (0,2] \). Our aim in this work is to study the impact of the heavy tailed step distributions on the asymptotic behavior of the random walk. We shall see that, as for the ERW, the asymptotic behavior of the Shark Random Swim depends on its memory parameter p, and that a phase transition can be observed at the critical value \( p=\frac{1}{\alpha } \).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Baur, E., Bertoin, J.: The fragmentation process of an infinite recursive tree and Ornstein-Uhlenbeck type processes. Electron. J. Probab 20(98), 1–20 (2015)

    MathSciNet  MATH  Google Scholar 

  2. Baur, E., Bertoin, J.: Elephant random walks and their connection to Pólya-type urns. Phys. Rev. E 94, 052134 (2016). https://doi.org/10.1103/PhysRevE.94.052134

    Article  ADS  Google Scholar 

  3. Bercu, B.: A martingale approach for the elephant random walk. J. Phys. A 51(1), 015201 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Bercu, B., Laulin, L.: On the multi-dimensional elephant random walk. arXiv:1709.07345 (2017)

  5. Boyer, D., Romo-Cruz, J.C.R.: Solvable random-walk model with memory and its relations with Markovian models of anomalous diffusion. Phys. Rev. E 90, 042136 (2014). https://doi.org/10.1103/PhysRevE.90.042136

    Article  ADS  Google Scholar 

  6. Chlebus, E.: An approximate formula for a partial sum of the divergent p-series. Appl. Math. Lett. 22, 732–737 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Coletti, C.F., Gava, R., Schütz, G.M.: Central limit theorem for the elephant random walk. J. Math. Phys. 58, 053303 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  8. da Silva, M.A.A., Cressoni, J.C., Schütz, G.M., Viswanathan, G.M., Trimper, S.: Non-Gaussian propagator for elephant random walks. Phys. Rev. E 88, 022115 (2013). https://doi.org/10.1103/PhysRevE.88.022115

    Article  ADS  Google Scholar 

  9. Janson, S.: Limit theorems for triangular urn schemes. Probab. Theory Relat. Fields 134(3), 417–452 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Klammler, F., Kimmich, R.: Geometrical restrictions of incoherent transport of water by diffusion in protein or silica fineparticle systems and by flow in a sponge. A study of anomalous properties using an NMR field-gradient technique. Croat. Chem. Acta 65, 455–470 (1992)

    Google Scholar 

  11. Kürsten, R.: Random recursive trees and the elephant random walk. Phys. Rev. E 93, 032111 (2016). https://doi.org/10.1103/PhysRevE.93.032111

    Article  ADS  MathSciNet  Google Scholar 

  12. Mahmoud, H.: Polya Urn Models. Chapman & Hall/CRC, London (2008). ISBN 1420059831, 9781420059830

  13. Möhle, M.: The Mittag-Leffler process and a scaling limit for the block counting process of the Bolthausen-Sznitman coalescent. Lat. Am. J. Probab. Math. Stat. 12(1), 35–53 (2015)

    MathSciNet  MATH  Google Scholar 

  14. Murase, K., Fujiwara, T., Umemura, Y., Suzuki, K., Iino, R., Yamashita, H., Saito, M., Murakoshi, H., Ritchie, K., Kusumi, A.: Ultrafine membrane compartments for molecular diffusion as revealed by single molecule techniques. Biophys. J. 86, 4075–4093 (2004)

    Article  Google Scholar 

  15. Schütz, G.M., Trimper, S.: Elephants can always remember: exact long-range memory effects in a non-Markovian random walk. Phys. Rev. E 70, 045101 (2004). https://doi.org/10.1103/PhysRevE.70.045101

    Article  ADS  Google Scholar 

  16. Serva, M.: Scaling behavior for random walks with memory of the largest distance from the origin. Phys. Rev. E 88, 052141 (2013). https://doi.org/10.1103/PhysRevE.88.052141

    Article  ADS  Google Scholar 

  17. Sims, D.W., Southall, E.J., Humphries, N.E., Hays, G.C., Bradshaw, C.J.A., Pitchford, J.W., James, A., Ahmed, M.Z., Brierley, A.S., Hindell, M.A., Morritt, D., Musyl, M.K., Righton, D., Shepard, E.L.C., Wearmouth, V.J., Wilson, R.P., Witt, M.J., Metcalfe, J.D.: Scaling laws of marine predator search behaviour. Nature 451(7182), 1098–1102 (2008)

    Article  ADS  Google Scholar 

  18. Wang, K.G.: Long-time-correlation effects and biased anomalous diffusion. Phys. Rev. A 45, 833–837 (1992). https://doi.org/10.1103/PhysRevA.45.833

    Article  ADS  Google Scholar 

Download references

Acknowledgements

I would like to thank Jean Bertoin for introducing me to this topic and for his advice and support. I would also like to thank two anonymous referees for their careful reading of an earlier version of this work and their helpful comments.

Author information

Authors and Affiliations

  1. Institut für Mathematik, Universität Zürich, Winterthurerstrasse 190, 8057, Zurich, Switzerland

    Silvia Businger

Authors
  1. Silvia Businger
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Silvia Businger.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Businger, S. The Shark Random Swim. J Stat Phys 172, 701–717 (2018). https://doi.org/10.1007/s10955-018-2062-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10955-018-2062-5

Keywords

Search

Navigation